基于距離哈希的稀疏點集快速匹配算法研究

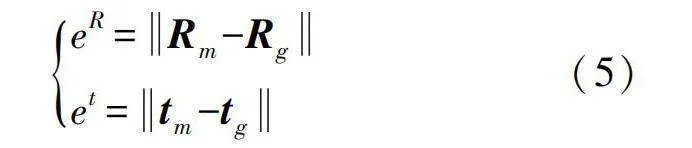
摘 要：針對不同坐標系下部分重疊的稀疏坐標點集，提出一種基于距離哈希的同名點快速穩健匹配算法。將各點與其鄰近點的距離關系映射成一個二進制碼身份標簽，通過身份標簽相似度計算，找出兩個點集中滿足設定閾值的候選匹配點對，從而建立初始匹配關系。據此計算剛體變換矩陣對兩組點集進行配準，確定兩組點集之間的精確匹配關系。實驗結果表明：該算法不僅速度快、準確率高、對于噪點和低重疊度具有穩健性，而且對兩個點集之間的初始相對位置沒有任何限制。

關鍵詞：機器視覺；稀疏點集；點集匹配；距離哈希；二進制碼

中圖分類號：TP391.7 文獻標志碼：B 文章編號：1671-5276（2024）04-0169-04

Research on Sparse Point Set Fast Matching Algorithm Based on Distance Hash

WU Linpeng，ZHOU Ling，YANG Han，ZHAO Jiayi，ZHANG Liyan

（Nanjing University of Aeronautics and Astronautics，Nanjing 210016， China）

Abstract：Based on distance hash， proposes a fast and robust matching algorithm with homonymous points for partially overlapping sparse coordinate point tsets in different coordinate systems. A binary code identity tag is mapped according to the distance relationship between each point and its adjacent points. Through the similarity calculation of identity tags， the corresponding similar point pairs meeting the set threshold in two point sets are found to establish the initial matching， based on which， the rigid body transformation matrix is calculated to register the two point sets， and the precise matching between the two point sets is defined. The experiment results show that the proposed algorithm is fast， accurate， robust to noises and low overlapping， and hasno restriction on the initial relative position between two point sets.

Keywords：machine vision；sparse point sets；point sets matching；distance hash；binary code

0 引言

點云配準技術是針對激光掃描儀、結構光測量系統等設備所獲得的同一物體在不同視角下的海量點云數據進行合并的技術。最經典的點云配準算法是由BESL等^[1]提出的最近點迭代算法（iterative closest point， ICP），通過反復迭代尋找最佳同名匹配點對，以估計變換矩陣。但算法的運行速度和收斂性很大程度取決于點云的初始位姿，目標函數還易陷入局部最優的情況，故需要粗配準^[2-3]為其提供初始位姿，常作為二次精配準使用。

一種影響廣泛的經典粗配準方法基于全等4點集（4-points congruent sets，4PCS）^[4]，通過在目標點云和源點云之間尋找具有相同拓撲結構的4點對，來計算兩個點集之間的變換矩陣，對噪聲、遮擋和異常值具有較高的魯棒性，4PCS算法的主要問題在于比較慢，提取相似集和驗證變換都比較耗時。Super 4PCS^[5]、volumetric 4PCS^[6]、voxel 4PCS^[[7]等方法都致力于提高4PCS的速度，但對于工業應用仍然配準精度較低，配準速度也難以滿足一些較復雜應用的要求。

基于哈希的文件檢索方法^[8]是近年來廣受關注的在海量數據中尋找相似文檔的方法。它的基本思想是通過找到一個合適的哈希函數，將數據庫中的每個項目映射為一個簡單的二進制代碼，并且使得相似的項目具有相似的二進制代碼。受上述基于哈希方法的二進制編碼在相似性匹配和檢索中成功應用的啟發，本文針對部分重疊的稀疏點集的同名點匹配問題，提出一種基于距離哈希的二進制編碼的快速穩健匹配方法。

1 基于哈希的稀疏點云匹配算法

給定同一物體從任意兩個不同角度獲得的三維點集P和Q，若存在匹配點對集合C{p_i，q_j（i=1，2，…，m，j=1，2，…，n），其中?p_i P，q_j Q，T（p_i）－q_j≤δ都成立，δ為較小常數，T為點集P和Q之間的剛性變換。則當集合C含有元素數量最多時，兩個點集之間的剛性變換為最佳剛性變換T_best，此時記C=C_max為最大匹配公共集。最大公共集（largest common pointset，LCP）問題^[9]就是通過不斷比較元素尋求C_max，從而獲得兩個點集之間的最佳剛性變換。LCP是點集配準技術要達到的目標，也是衡量配準質量的一個標準。

1.1 距離哈希編碼

對點集P中任一點p_i，可以借助k-d樹^[10]快速為其查找自身所在點集中的K個鄰近點p_ik（k=1，2，…，K），隨后將點p_i與p_ik之間的歐氏距離轉化為二進制身份碼，如圖1所示。為了更清楚地展示編碼過程，圖1中僅顯示p_i的6個鄰近點。

在對兩個點集P和Q中的點進行二進制編碼時，首先會設立一個長度為l的固定步長，將歐氏距離轉化為步數S。在點p_i與其K個鄰近點p_ik的距離中，d_max為最大距離。對d_max/l向上取整作為該身份碼的長度S，即

S=ceil（d_max/l）（1）

根據S和l為p_i建立一個二進制位數組I_D，pi，該數組含二進制位個數為S，每一位初始值為0。鄰近點中p_ik與p_i之間的歐氏距離為d_ik，轉化成步數s_ik為

s_ik=ceil（d_ik/l）（2）

若二進制位數組I_D，pi的第s_ik位為1，則等價于p_i在步數為s_ik的位置存在一個鄰近點。將每個鄰近點映射到p_i的二進制數組上，則點p_i與其K個最鄰近點之間的距離特征被轉換為二進制碼I_D，pi，定義I_D，pi為點p_i的二進制身份標簽。

1.2 相似度比較

通過上一節距離哈希算法，將點集P和Q中的數據點與其臨近點之間的距離關系映射為二進制身份編碼，從而使得點集中任一點都具有一個二進制碼身份標簽。該身份標簽在保留原點集各點與其鄰近點之間距離特征的同時大大簡化了數據的存儲。在完成兩個點集中所有數據的二進制身份編碼后，將點集P中數據的身份標簽與點集Q中數據的身份標簽逐一進行對比，即對二進制碼I_D，pi（i=1，2，…，m）和I_D，qj（j=1，2，…，n）進行按位“與”運算，將其結果記為r=I_D，piamp;I_D，qj，計算r中二進制位值為1的總位數N_r，則兩點之間的相似度M為

M=2N_r/（N_pi+N_qj）（3）

式中N_pi和N_qj分別為I_D，pi和I_D，qj中二進制位值為1的總位數。在點集Q中循環，求出使M最大的序號J，并記最大相似度M=M_max，若M_max的值大于設定閾值β，則可認為p_i和q_J是一對候選匹配點對。經過上述相似度計算和比較后，可獲得點集P和Q之間的初始匹配點對集合C_f。

1.3 基于最鄰近點的精確匹配

在初始匹配點對集合C_f內，點對之間可能存在誤匹配的情況，而其中相似度較大的一些點往往是正確的匹配點對。因此，本文在集合C_f中，取相似度最大的L個點對計算初始剛體變換T_f（R_f，t_f），將點集P中的各點轉換至Q所在的坐標系下，即做變換：

p^f_i=R_fp_i+t_f（4）

經過變換后的點集P和Q中的匹配點對應該具有相近的位置，對應點間距離應在三維測量產生的誤差范圍內。為此，通過查找最鄰近點的方法來進行更精確的匹配。在點集Q所形成的k-d樹中搜索p^f_i的最鄰近點q_rst，當最鄰近點p^f_i與q_rst的距離小于兩組點云的測量誤差之和時，則認為p_i和q_j是一對正確的匹配點。最終獲得精確匹配點對集合C_max。在集合C_max基礎上通過奇異值分解算法（singular value decomposition， SVD），即可求解P和Q之間的剛體變換矩陣，進而完成點集之間的配準。

2 實驗結果與分析

為驗證本文算法效果，以工業中常見且具有不同表面特征的直升機和汽車為例進行測試，所采用實驗數據為自主研發的工業近景攝影測量軟件所獲得的直升機尾部和汽車的特征點集數據。

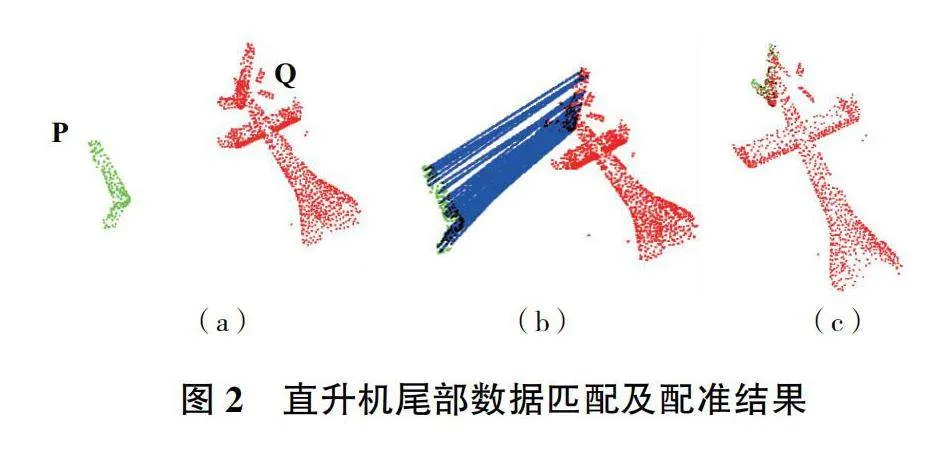
圖2顯示了對直升機尾部數據進行匹配及配準的結果。圖2（a）中，P為直升機尾部測量數據，Q為直升機尾部數據的一部分，與P之間存在旋轉角度為45°，平移為{1 000， 2 000， 0}的剛體變換，并添加均值為0、方差為0.2的高斯白噪聲，P和Q含數據點個數分別為1 220和190。圖2（b）為采用本文算法對兩組點集進行匹配的結果，每條藍色線段連接了一對匹配點對（本刊黑白印刷，相關疑問咨詢作者）。圖2（c）顯示在正確的匹配點對集合基礎上，通過方程求解計算實現了點集之間的配準。

在三維測量過程中，由于測量角度或測量方式的不同，兩個點集P和Q之間可能存在以下不同重疊關系：①Q為P的一部分；②P和Q存在部分交叉；③Q為P存在數據缺失情況下P的較稀疏點集。因此，本文采用直升機尾部和汽車點集數據，分別對以上3種不同情況進行測試。如圖3所示的汽車數據及圖4的直升機尾部數據，第1到第3組分別對應了兩組點集重疊關系為以上①、②和③的情況。同時，實際測量過程中也會存在噪聲干擾等情況。為模擬實際環境，分析算法的魯棒性和配準精度，實驗中為Q添加均值為0、方差為0.3的高斯白噪聲，并在兩點集之間產生0°～360°之間任意角度的旋轉和隨機平移。在情況③下，Q較P具有50%的隨機數據丟失。考慮到由于稀疏點集無法提供法向量、曲率或其他線、面等特征，多數配準算法對此不適用，經典的4PCS方法基于同一平面4點組仿射不變性尋找對應關系，雖不受此類限制，但速度過慢，將本文算法與其較成熟的改進算法super 4PCS方法進行比較。

本文以旋轉誤差和平移誤差來評估配準效果。首先將旋轉矩陣R轉化為按照固定順序z-y-x內旋的歐拉角，采用歐拉角來計算旋轉誤差e^R。旋轉誤差和平移誤差分別被定義如下：

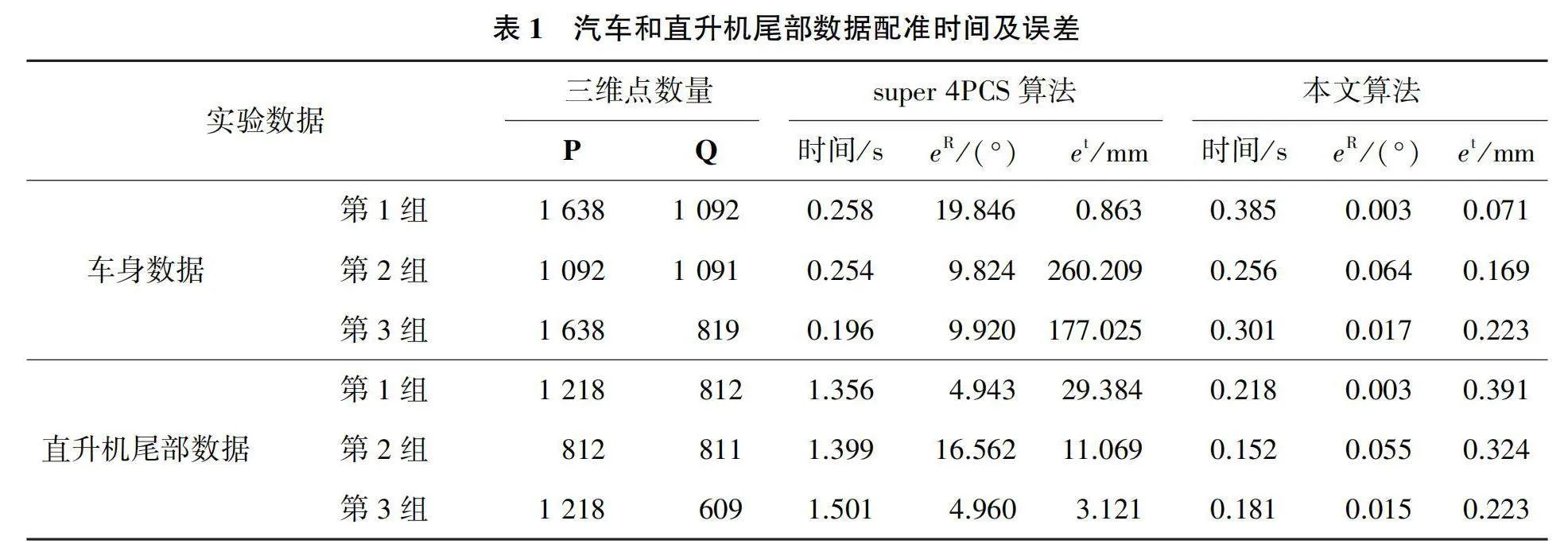
式中{R_m，t_m}和{R_g，t_g}分別表示剛體變換的實際值和估計值。為進一步比較配準性能，表1中列出了圖3和圖4中各組不同數據分別采用super 4PCS和本文算法時所用時間及誤差。對圖3、圖4和表1的數據進行分析可以看出，在配準精度上，本文算法較super 4PCS具有較大優勢，對兩點集處于各種不同重疊關系均能獲得準確的配準結果。在速度方面，對于汽車數據，雖然super 4PCS速度較快，但得到的配準結果均有較大偏差。根據文獻[5]，super 4PCS雖然優化了提取4點集的時間，但在點集驗證過程的速度仍然沒有太大改善，對文中點數不多的模型進行配準時仍然異常耗費時間。在本文直升機尾部數據實驗中，其耗費時間也較長，而本文算法則能快速穩定地獲取正確配準結果。可見本文算法對于三維視覺測量中所獲得的稀疏點集之間的匹配和配準具有重要意義。

3 結語

本文對基于標記點的三維視覺測量所獲得的稀疏點集數據，提出一種基于距離哈希的快速匹配方法。將點集中任一點與鄰近點的距離在剛體變換下的不變性作為點集匹配的特征，通過距離哈希方法將距離關系映射為一個二進制碼身份標簽，快速的二進制碼相似度計算方法能夠實現點集間同名匹配點的高效查找。最后通過基于k-d樹的最鄰近點查找方法進行距離校驗，從而實現點集間的精匹配。基于汽車和直升機尾部測量數據的多個實驗表明，本文算法速度快，準確率高，對噪點及各種不同重疊情況具有穩健性，且對兩個點集之間的初始位置沒有任何限制，對于表面形狀復雜的物體亦能獲得良好的結果。

參考文獻：

[1] BESL P J，MCKAY N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，1992，14（2）：239-256.

[2] DíEZY，ROUREF，LLADóX，et al. A qualitative review on 3D coarse registration methods[J]. ACM Computing Surveys，2015，47（3）：1-36.

[3] BUENO M， GONZáLEZ J ， MARTíNEZ S， et al. Automatic point cloud coarse registration using geometric keypoint descriptors for indoor scenes[J]. Automation in Construction，2017，81：134-148.

[4] AIGER D，MITRA N J，COHEN-OR D. 4-points congruent sets for robust pairwise surface registration[J]. ACM Transactions on Graphics，2008，27（3）：1-10.

[5] MELLADO N，AIGER D，MITRA N J. Super 4PCS fast global pointcloud registration via smart indexing[J]. Computer Graphics Forum， 2014， 33（5）： 205-215

[6] HUANG J D，KWOK T H，ZHOU C. V4PCS：volumetric 4PCS algorithm for global registration[J]. Journal of Mechanical Design，2017，139（11）：111403.

[7] XU Y S， BOERNER R， YAO W，et al. Pairwise coarse registration of point clouds in urban scenes using voxel-based 4-planes congruent sets[J]. ISPRS Journal of Photogrammetry and Remote Sensing， 2019， 151： 106-123.

[8] TIAN D H， JIA X Q， MA R， et al. BinDeep： a deep learning approach to binary code similarity detection[J]. Expert Systems with Applications， 2021，168：114348.

[9] JUAREZ PAULINO D S ， DIBIO L B， FLAVIO B V. A dynamic approach for approximate pairwise alignment based on 4-points congruence sets of 3D points[C]//2011 18th IEEE International Conference on Image Processing， Brussels，Belgium：IEEE，2011：889-892.

[10] BENTLEY J L. Multidimensional binary search trees used for associative searching[J]. Communications of the ACM，1975，18（9）：509-517.

收稿日期：2023-02-15