一種星座遮擋場景下的GNSS接收機選星策略

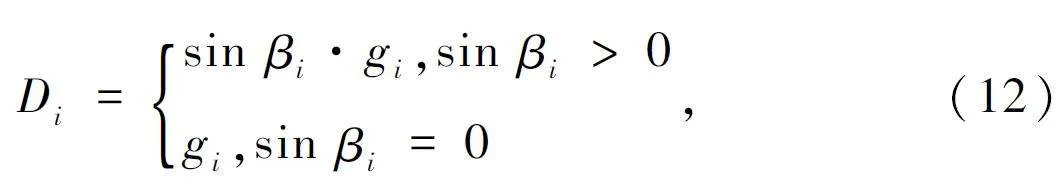
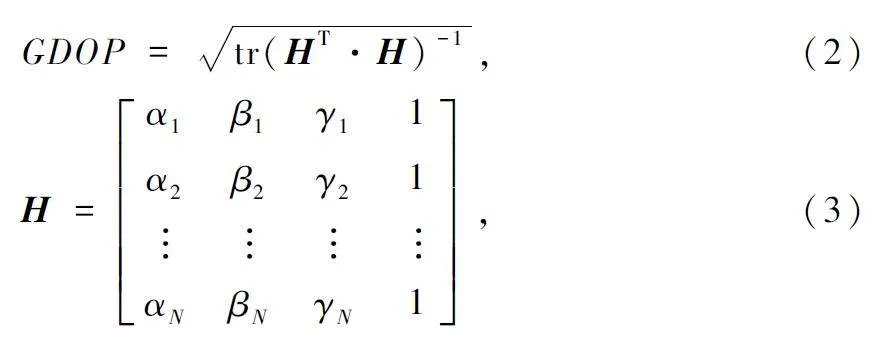
摘 要：ＧＮＳＳ 接收機在城市、密林和峽谷等環境下工作時，衛星信號受遮擋嚴重，造成星座殘缺情況。針對北斗衛星導航定位系統中傳統的最大四面體體積法不能有效反映遮擋情況的問題，提出了一種基于幾何精度因子（ＧｅｏｍｅｔｒｉｃＤｉｌｕｔｉｏｎ Ｐｒｅｃｉｓｉｏｎ，ＧＤＯＰ） 值分析的新型選星策略。設置高度角閾值，在滿足閾值條件下結合衛星高度角、方位角，分析幾何布局，通過構造最大四面體體積選出參與定位解算的衛星組合。經計算機仿真驗證分析得出，在星座遮擋場景下該算法相較于最佳ＧＤＯＰ 算法計算量減少了９５％ 以上，相比最大四面體體積法性能提升了２． ６２ ｄＢ，在保證定位精度的同時實現了準確快速的選星，具有良好的性能和可行性。

關鍵詞：幾何精度因子；選星策略；幾何布局；方位角

中圖分類號：Ｐ２２８． ４；ＴＮ９６７． １ 文獻標志碼：Ａ 開放科學（資源服務）標識碼（ＯＳＩＤ）：

文章編號：１００３－３１０６（２０２４）０７－１６８７－０７

０ 引言

隨著衛星導航系統應用深入社會經濟生活的各個領域，針對提升導航接收機性能的研究也愈發豐富。定位精度作為評價導航接收機性能的關鍵指標，其誤差來源［１］主要分為兩方面：一是接收機硬件設計欠妥或環境因素較為惡劣，破壞了導航信號完整性從而引發定位誤差；二是在接收機定位解算時選星策略設計不恰當，導致定位精度下降。接收機硬件受限于設計成本，且環境因素不可控，因此提升接收機定位精度［２］的研究往往從優化選星策略的方向開展。

北斗三代成功組網后，北斗全球導航系統的在軌衛星達４０ 余顆。衛星數目的增加為接收機定位提供便利的同時也提升了選星策略設計的復雜度［３］。此外，在城市、森林和峽谷等環境下，衛星信號傳播受阻，使得導航接收機工作在星座遮擋場景下。因此設計一種在星座遮擋場景下的導航接收機選星策略具有較強的應用價值和現實意義。

傳統的選星策略包括最佳幾何精度因子（Ｇｅｏ-ｍｅｔｒｉｃ Ｄｉｌｕｔｉｏｎ Ｐｒｅｃｉｓｉｏｎ，ＧＤＯＰ）法和最大四面體體積法兩大類。對于最佳ＧＤＯＰ 法，文獻［４］對行列式矩陣進行加權，文獻［５］通過分析衛星對ＧＤＯＰ值計算的貢獻進行選星，但該類方法運算中需要頻繁構建并操作高維矩陣，計算量大且實現復雜，對算法的實現載體要求較高。最大四面體體積法通過分析ＧＤＯＰ 和幾何布局的關系，使參與定位的衛星構成的四面體體積最大，得到更低的ＧＤＯＰ 值。文獻［６］根據高度角進行分區，再通過方位角進行篩選最終成功選出合適的衛星組合，但該算法在衛星星座遮擋場景下，選星算法得到的衛星分布不是最優解，所構成四面體體積不能達到最大，ＧＤＯＰ 值不夠低。為了進一步提高星座遮擋場景下接收機定位精度，本文基于最大四面體體積法提出一種基于星座遮擋場景的導航接收機選星策略，該方法兼顧高度角、方位角和ＧＤＯＰ 值，具有一定的參考和應用價值。

１ 定位精度

作為評價導航接收終端定位準確與否的重要標準，定位精度取決兩大因素：一是接收終端的觀測量誤差；二是終端所接收信號的衛星星座分布情況［７－８］，表達式如下：

Δｘ ＝ Δρ·ＧＤＯＰ， （１）

式中：Δｘ 表示接收終端定位精度的標準偏差，Δρ 表示觀測量標準偏差，ＧＤＯＰ 表示幾何精度因子。

受大氣延時、多徑效應、電磁干擾和地球自轉等影響［９］，計算偽距觀測量時會不可避免地產生誤差，由式（１）可知，當Δρ 已知時Δｘ∝Δρ，ＧＤＯＰ 表征了衛星幾何分布引起的觀測量誤差與接收終端定位誤差之間的比例關系［１０］。因此，通常通過降低ＧＤＯＰ 的值來減小定位誤差，提升定位精度。

ＧＤＯＰ 是評價導航衛星空間幾何分布的重要指標［１１］，反映了定位衛星星座的拓撲結構對觀測量誤差的放大程度［１２］，是衡量導航系統定位性能的重要指標，計算如下：

式中：ｔｒ 表示對矩陣取跡，Ｈ 表示衛星導航系統的觀測矩陣，［αｉ βｉ γｉ ］分別表示Ｘ、Ｙ、Ｚ 方向的余弦矢量，ｉ 表示參與定位解算的衛星號。

北斗單系統定位時，需要有４ 顆衛星的測量值才能解出ｘ、ｙ、ｚ 和接收機鐘差４ 個未知數。當參與定位的衛星個數為４ 時，由文獻［１１］的推論可知，ＧＤＯＰ 與衛星和接收終端構造的四面體體積Ｖ 的關系可表示為［１１］：

式中：Ａ 為ｔｒ（ＨＴ Ｈ）* ，矩陣Ｈ 取決于衛星可見個數及其相對于用戶的幾何分布［１３］，所以Ａ 是一個常數。隨著Ｖ 的增大，衛星的坐標發生變化，導致方向余弦矢量變化，但是相較于體積變化，這種變化幅度較小，由于是由Ａ 對矩陣Ｈ 運算后取跡再開方得出，所以當Ｖ 增大時，可以將根號Ａ 視為一個常數值。

綜上分析可知，ＧＤＯＰ 值會隨著Ｖ 的增大而減小，即衛星與接收終端所構成四面體體積越大，由該組衛星所計算出的ＧＤＯＰ 越小，接收終端的定位效果越優良。

２ 衛星星座

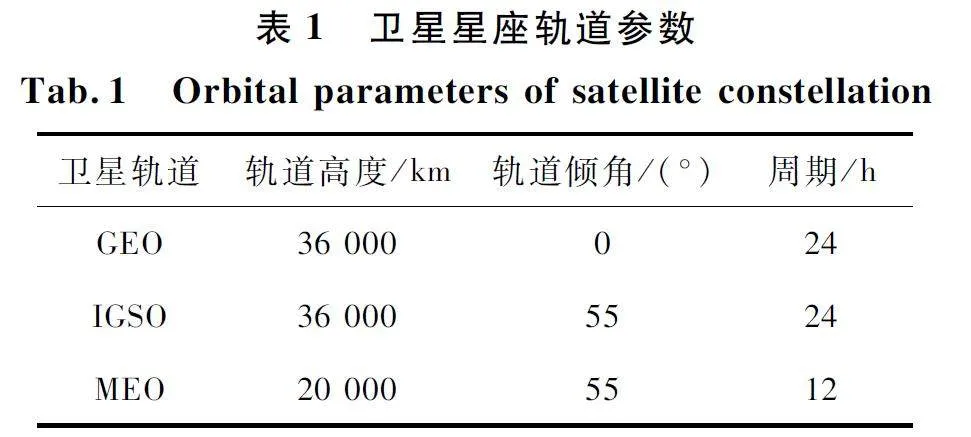
北斗衛星導航系統空間段包括３５ 顆衛星，分為３ 種，分別是５ 顆地球靜止軌道（Ｇｅｏｓｔａｔｉｏｎａｒｙ Ｏｒｂｉｔ，ＧＥＯ）衛星、２７ 顆中軌道（Ｍｅｄｉｕｍ Ｅａｒｔｈ Ｏｒｂｉｔ，ＭＥＯ）衛星以及３ 顆傾斜軌道同步（Ｉｎｃｌｉｎｅｄ Ｇｅｏｓｙｎ-ｃｈｒｏｎｏｕｓ Ｏｒｂｉｔ，ＩＧＳＯ）衛星，３ 種衛星的具體軌道參數如表１ 所示。

各個軌道衛星按照相應周期規律運行，均勻分布在衛星星座中。

３ 星座遮擋場景下的選星策略

３． １ 傳統算法

傳統選星算法主要分為最佳ＧＤＯＰ 法和最大四面體體積法２ 類。其中最佳ＧＤＯＰ 法是以遍歷輪詢的方法，對可見星進行組合，依次計算其ＧＤＯＰ值，選出ＧＤＯＰ 值最小的衛星組合參與定位解算。但是可見星數量較多時，該算法運算量較大。假設接收星座可見衛星數為１５ 時，選４ 顆衛星進行定位解算，就需要進行Ｃ４１５ ＝ １ ３６５ 次運算對比，每次運算中包含大量的矩陣相乘與矩陣求逆，所需的運算時間長，接收終端運算負擔較大，選星結果不具有實時性。

最大四面體體積法的核心思想就是在接收星座中首先確定一顆頂座星［１４］，然后輪詢余下衛星，使得衛星構成的四面體體積最大，如式（５）所示，即可獲得更小的ＧＤＯＰ 值。最大四面體體積法的步驟總結如下：

① 假設可見星數為ｎ，在可見星中選出高度角最大的衛星作為頂座星，記為Ｓ１ 。

② 遍歷組合余下的ｎ － １ 顆衛星，選出底座星［１１］Ｓ２ 、Ｓ３ 、Ｓ４ 與Ｓ１ 構成四星組合。

③ 計算每個組合的四面體體積，記作Ｖｉ。

④ 從｛Ｖ１ ，Ｖ２ ，…，Ｖｇ｝中選出最大的體積對應的衛星組合（ｇ 為遍歷得出的組合數），作為最佳組合參與到后續的定位解算中。

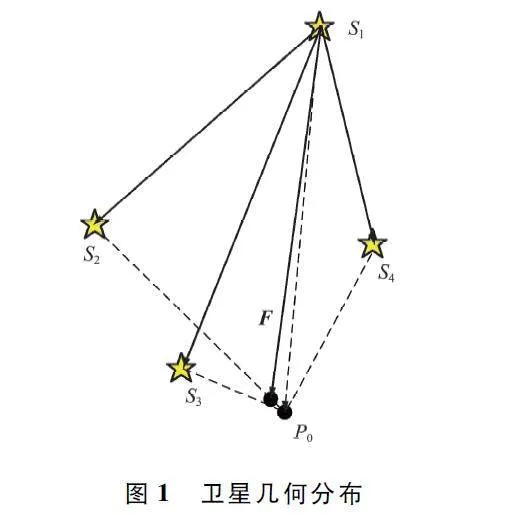
最大四面體體積法還可以從向量角度進行分析，先確定頂座星作為向量的起點即Ｓ１ ，再將底座星作為向量的終點，求和向量，選和向量最接近Ｓ１ Ｐ０ 的組合作最佳組合。

Ｆ ＝ Ｓ１ Ｓ２ ＋ Ｓ１ Ｓ３ ＋ Ｓ１ Ｓ４ 。（６）

向量Ｓ１ Ｓ２ 、Ｓ１ Ｓ３ 、Ｓ１ Ｓ４ 的大致分布如圖１ 所示。

當向量Ｆ 的方向為頂座星Ｓ１ 指向最終定位結果時定位效果最佳，所以當向量Ｆ 越接近Ｓ１ Ｐ０ ，定位效果越好。構造函數模型：

式中：γ 為向量Ｆ 與Ｓ１ Ｐ０ 的夾角。當底座星Ｓ２ 、Ｓ３ 、Ｓ４ 與Ｓ１ 連線的夾角接近相等時，和向量Ｆ 越接近Ｓ１ Ｐ０ ，Ｗ 值越大，此時構造的四面體體積最大，ＧＤＯＰ 值越小，定位效果越好。關系如式（８）所示，因此Ｗ 值可以用作衡量ＧＤＯＰ 替代條件。

Ｗ ∝ Ｖ ∝ １／ＧＤＯＰ。（８）

３． ２ 新型選星策略

以上２ 種傳統算法在可見星數量增多的情況下均無法保證選星的時效性。除此之外，當衛星星座受遮擋時，最大高度角［１５］衛星作頂座星計算出的結果Ｗ 不是最優情況，所以在星座遮擋場景下選擇最大的高度角作頂座星的方法并不適用，會損失一定的定位精度。

因此，本文設計了一種星座遮擋場景下的導航接收機選星策略，具體流程如圖２ 所示。

３． ２． １ 流程原理及數學模型分析

衛星信號在傳播過程中會受到電離層、對流層等時延誤差的影響，受影響的程度與衛星高度角密切相關［１６］。高度角越低，信號受到延遲誤差影響越大，越可能受到地面障礙物的遮擋。因此設置高度角閾值篩選［１７］，以減弱上述因素影響。

假設閾值篩選后的衛星為Ｓ１ ，Ｓ２ ，Ｓ３ ，…，ＳＮ ，計算每２ 顆衛星之間的方位角差值θｊ，如式（９）所示。為保證星座遮擋場景下的方位完整性，選最大差值Ｌ 對應的衛星組合作為邊緣星，記為Ｓ１ 、Ｓ２ 。

θｊ ＝ Ａｚｍ － Ａｚｎ ， （９）

Ｌ ＝ ｍａｘ｛θ１ ，θ２ ，…｝， （１０）

式中：ｊ 表示兩兩組合的排列序號；ｍ，ｎ∈（１，Ｎ）且ｍ≠ｎ，表示衛星Ｓｍ 、Ｓｎ 的編號；Ａｚｍ 、Ａｚｎ 表示對應衛星的方位角。

確定好邊緣星后，計算出過邊緣星連線中點的垂面，記為α。

α：Ａ（ｘ － ｘ０ ）＋ Ｂ（ｙ － ｙ０ ）＋ Ｃ（ｚ － ｚ０ ） ＝ ０， （１１）

式中：（ｘ０ ，ｙ０ ，ｚ０ ）為邊緣星連線的中點坐標，（Ａ，Ｂ，Ｃ）為平面的法向量Γ，即邊緣星構成的方向向量。

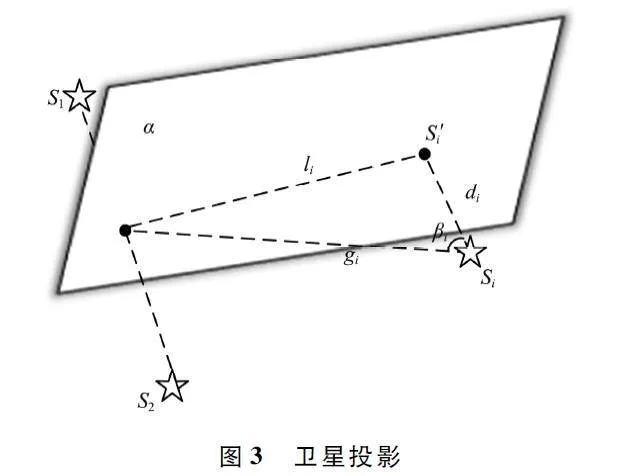
將剩余可見星投影到平面α，根據投影點Ｓ′ｉ 到邊緣星中點的距離ｌｉ 與該衛星Ｓｉ 到平面α 的距離ｄｉ，在ｄｉ 盡可能小的情況下，選擇足夠大的ｌｉ 作頂座星，記為Ｓ３ ，如圖３ 所示。

計算邊緣星中點到Ｓｉ 的距離，記為ｇｉ。為找出距離２ 顆邊緣星最遠的頂座星，提出聯合構建的函數模型Ｄｉ，如式（１２）所示，選擇ｍａｘ ｛Ｄ１ ，Ｄ２ ，…，ＤＮ－２ ｝對應的衛星作頂座星。在衛星星座殘缺場景下，通過結合目前方位上殘缺的角度以及剩余衛星的高度角、方位角，在保證方位上較為完整的前提下選出當前情況下的最佳頂座星。

式中：βｉ 為衛星Ｓｉ 與平面α 夾角的余角。

最后遍歷余下的可見星，記為Ｓｋ，加上已選的３ 顆衛星，構成４ 星組合，計算四面體體積記作Ｖｋ，將體積最大的組合作為最佳組合。

３． ２． ２ 策略步驟

本文提出的新型選星算法的具體步驟總結如下：

① 設置高度角閾值［１８］為１０°，對可見星進行篩選。

② 在可用衛星數大于４ 前提下，計算兩兩衛星之間的方位角差值。

③ 選出最大差值Ｌ，找出對應衛星組合作為邊緣星，記為Ｓ１ 、Ｓ２ 。

④ 根據邊緣星，通過投影法參考函數模型Ｄｉ，選出頂座星記為Ｓ３ 。

⑤ 最后在余下的可見星中遍歷與已選的３ 顆衛星構成４ 星組合，計算體積，選體積最大的組合作為最佳組合。

４ 算法仿真與結果分析

４． １ 仿真測試環境

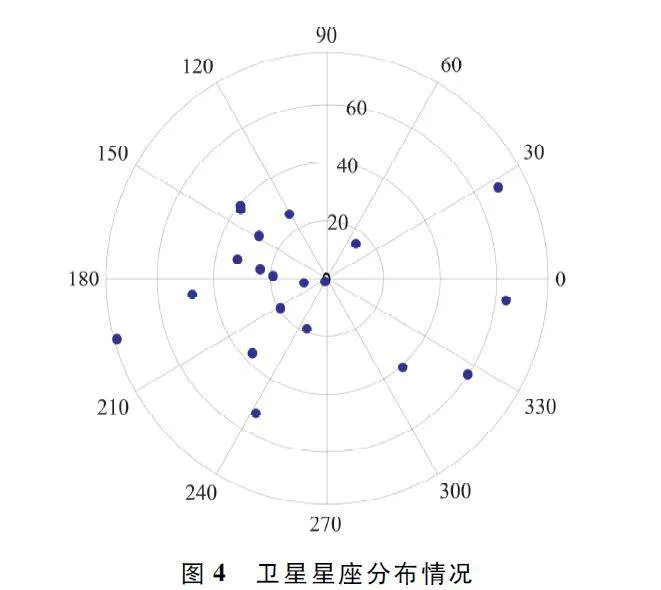
實驗數據由衛星工具包（Ｓｙｓｔｅｍｓ Ｔｏｏｌ Ｋｉｔ，ＳＴＫ）導出，首先導入北斗衛星導航系統信息，接著選擇用戶位置信息，本文使用的用戶位置選在經度１１４． ４°，緯度３８°的地區，最后設置歷元信息，導出衛星高度角、方位角以及衛星位置等參數信息。導出實驗數據后，在Ｗｉｎｄｏｗｓ １１ 系統下進行計算機仿真實驗，衛星分布情況如圖４ 所示（歷元設置在２０２２ 年６ 月１ 日１０ 時的衛星星座分布情況）。

４． ２ 性能仿真分析

仿真實驗中的變量為衛星數和遮擋角度［１９］，其中遮擋角度代表隨機的遮擋范圍，衛星數代表星座受遮擋前的衛星數量，導出不同歷元信息的實驗數據，進行Ｍｏｎｔｅ Ｃａｒｌｏ 實驗，分別使用最佳ＧＤＯＰ 法、本文算法、最大四面體體積法進行選星，計算ＧＤＯＰ值。實驗數據來自ＳＴＫ 模擬導出，單一歷元條件下，可見衛星數量在２２ 左右，故實驗選取２０ 作為衛星數的最大值。

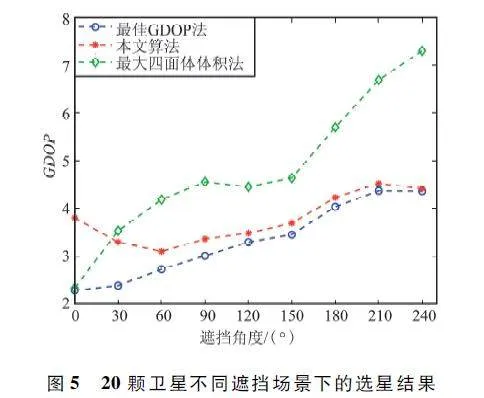
仿真實驗一：固定衛星數為２０，導入不同歷元的實驗數據，分別對不同遮擋程度下的衛星星座進行分析，３ 種算法的選星結果如圖５ 所示。

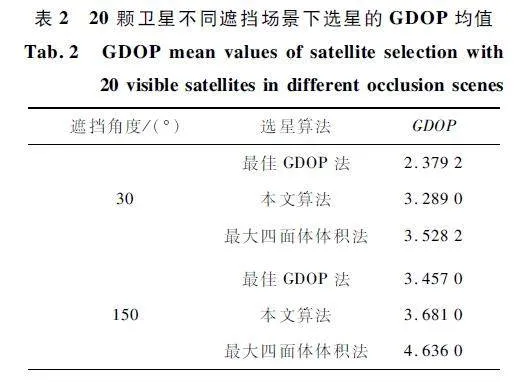
由圖５ 可以看出，當遮擋角度為０°時，本文算法相較于最大四面體體積法和最佳ＧＤＯＰ 法效果一般。但隨著遮擋角度的增加，本文算法的ＧＤＯＰ曲線穩步貼近最佳ＧＤＯＰ 法的ＧＤＯＰ 曲線。

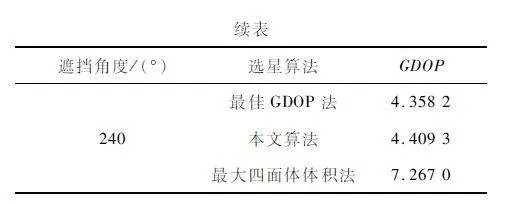
在星座遮擋場景下本文算法的優勢逐漸顯現出來，明顯效果優于最大四面體體積法，而最大四面體體積法的ＧＤＯＰ 曲線開始波動，漲幅變大，與最佳ＧＤＯＰ 法的差值逐漸拉大，選星的準確性難以保證。表２ 列出了幾個折線圖變化情況明顯對應的點，分別為３０°、１５０°、２４０°

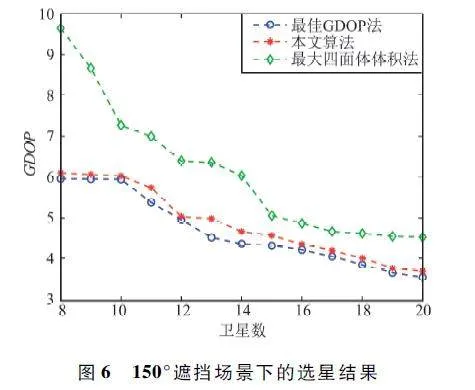
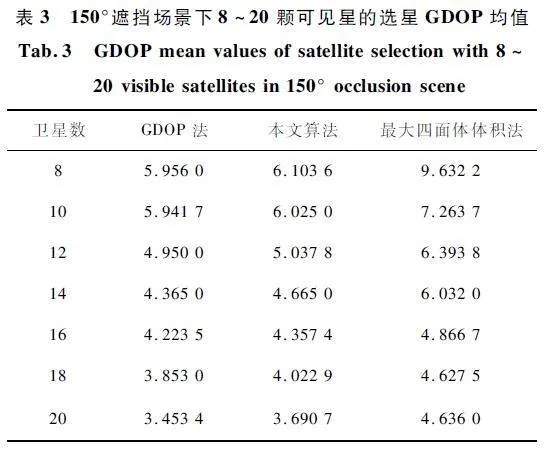
仿真實驗二：選取遮擋角度為１５０°，保證在星座遮擋場景下仍可滿足遮擋后可用衛星滿足基本定位需求（即大于４ 顆星），設置衛星數為８ ～ ２０，設置不同歷元導出數據，進行Ｍｏｎｔｅ Ｃａｒｌｏ 實驗，仿真結果如圖６ 所示。

分析圖６ 可知，當遮擋角度為１５０°時，本文算法選出的衛星組合計算出的最佳ＧＤＯＰ 法得到的ＧＤＯＰ 差值維持在０． ２ 左右，最小值為０． ０８，最大值約為０． ４，選星結果接近于最佳ＧＤＯＰ 法，曲線較為平穩，可以滿足基本的定位需求。

為方便更直觀地觀察ＧＤＯＰ 值變化情況，表３列出了偶數可見星選星后的ＧＤＯＰ 均值。

綜合圖表分析可知，在遮擋場景下隨著衛星數量的增加，本文算法優于最大四面體體積法，結果更接近于最佳ＧＤＯＰ 法，可以保證選星的準確性。

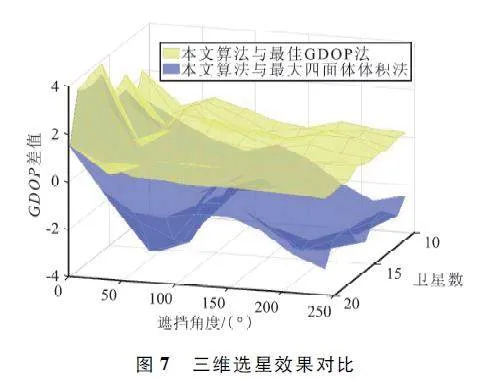
仿真實驗三：實驗變量設置為衛星數和星座遮擋角度，考慮到遮擋角度過大、衛星數過小會導致可用星不滿足定位需求的情況，本次仿真實驗將遮擋角度設置為０° ～ ２４０°，衛星數量設置為１０ ～ ２０ 顆，導出不同歷元的數據，在不同場景下采用上述３ 種算法進行選星。為更直觀看出本文算法的選星效果，計算本文算法與最佳ＧＤＯＰ 法、最大四面體體積法的ＧＤＯＰ 差值，仿真結果如圖７ 所示。

圖７ 上層圖像為本文算法減最佳ＧＤＯＰ 法得到的值，下層圖像為本文算法減最大四面體體積法得到的差值，其中Ｘ 軸為遮擋角度，Ｙ 軸為衛星的數量，Ｚ 軸表示ＧＤＯＰ 差值。計算表明，在星座遮擋場景下，相較于最佳ＧＤＯＰ 法，本文算法的ＧＤＯＰ 值增加了０． １１，與最大四面體體積法相比，本文方法提升了２． ６２ ｄＢ 的性能。

４． ３ 計算復雜度分析

４． ２ 節從性能角度進行分析并驗證得出本文算法在星座遮擋場景下的選星效果明顯優于最大四面體積法，且效果逼近最佳ＧＤＯＰ 法。

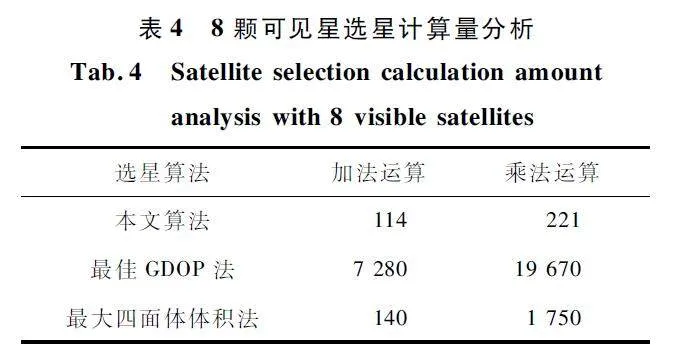
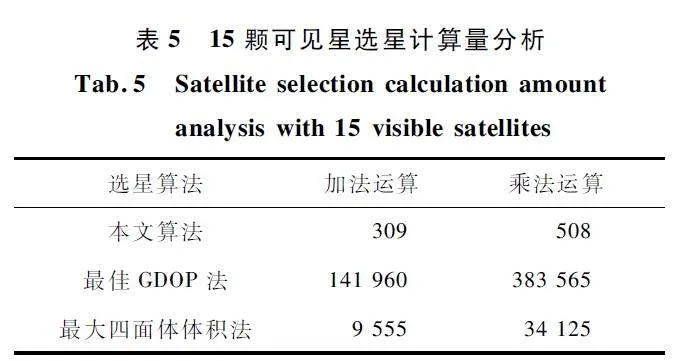
接著分析本文算法與２ 種傳統算法的計算復雜度。最佳ＧＤＯＰ 法每種組合都需要進行一次矩陣相乘和矩陣求逆運算，最大四面體體積法同樣地每次遍歷都需要進行一次體積計算。隨著衛星數的增加，２ 種傳統算法的運算量急劇增加，本文算法優勢明顯，為保證數據可靠性本節選用衛星數量較少與較多的８ 和１５ 進行運算量分析，具體的計算復雜度如表４ 和表５ 所示。

可見，對于最佳ＧＤＯＰ 法，無論是８ 顆星還是１５ 顆星，運算量均遠遠大于本文算法，相較于最佳ＧＤＯＰ 法選星，本文算法在可見星數量為８、１５ 顆的情況下乘法運算相對減少了９９． ８７６％ 、９９． ８６８％ ，加法運算減少了９８． ４３４％ 、９９． ７８２％ 。

５ 結束語

本文針對ＧＮＳＳ 提出了一種適用于星座遮擋場景下的選星策略，通過分析幾何布局充分利用衛星信息選出最佳組合參與定位解算。仿真結果表明，該策略在星座遮擋場景下選星效果極佳，相較于最大四面體體積法，本策略提升了２． ６２ ｄＢ 的性能，有效提高了選星的準確性，與最佳ＧＤＯＰ 法相差不大，可以滿足定位需求。該算法的運算量也較小，相較于最佳ＧＤＯＰ 法減少了９５％ 以上的計算量，提高了時效性，可以準確快速地進行選星，具有很重要的參考和應用價值。

參考文獻

［１］ 袁建平，羅建軍，岳曉奎，等． 衛星導航原理與應用［Ｍ］． 北京：中國宇航出版社，２００３．

［２］ 陳亮，李超，師鵬宇，等． ＢＤＳ ／ ＧＰＳ 組合導航定位研究［Ｊ］． 無線電工程，２０２０，５０（３）：２２７－２３１．

［３］ 郝雨時，孫劍偉，馬冬青． 北斗衛星導航系統功率增強選星策略設計與性能分析［Ｊ］． 導航定位學報，２０２１，９（２）：４１－４７．

［４］ 田安紅，付承彪，董德春，等． 一種改進的選星算法在ＧＰＳ 定位系統中的應用［Ｊ］． 海軍工程大學學報，２０１４，２６（２）：４５－４８．

［５］ 張昕，何柳，李燕敏，等． 一種基于高度角和ＧＤＯＰ 貢獻值的改進型選星算法［Ｊ］． 軟件導刊，２０１６，１５（８）：１６－２０．

［６］ 公才赫，茅旭初，李少遠． 一種ＢＤＳ ／ ＧＰＳ 雙系統融合導航的快速選星方法［Ｊ］． 上海交通大學學報，２０１７，５１（６）：６４１－６４６．

［７］ 黃健，巴曉輝，劉海洋，等． 一種基于定位誤差的多星座快速選星算法［Ｊ］． 科學技術與工程，２０１５，１５（１３）：８７－９１.

［８］ 汪鈺凱． ＧＮＳＳ 衛星導航精度與選星算法研究［Ｊ］． 無線電工程，２０１４，４４（７）：５４－５６．

［９］ 唐衛明，崔健慧，惠孟堂． 北斗區域星座對相對定位精度的影響分析［Ｊ］． 武漢大學學報（信息科學版），２０１６，４１（８）：１１０７－１１１２．

［１０］ 叢麗，ＡＢＩＤＡＴ Ａ Ｉ，談展中． 衛星導航幾何因子的分析和仿真［Ｊ］． 電子學報，２００６（１２）：２２０４－２２０８．

［１１］ 李克昭，王寧，魏金本，等． 基于一種不規則三角網的衛星導航選星算法研究［Ｊ］． 河南理工大學學報（自然科學版），２０２０，３９（１）：４７－５２．

［１２］ 馮彪，柴洪洲，潘宗鵬，等． 一種改進的組合導航系統選星算法［Ｊ］． 測繪工程，２０１８，２７（２）：２６－３１．

［１３］ 謝鋼． ＧＰＳ 原理與接收機設計［Ｍ］． 北京：電子工業出版社，２００９．

［１４］ 李衛東，韓景宇，王新屏，等． 一種北斗／ ＧＰＳ 雙模復合策略自適應快速選星算法［Ｊ］． 電子測量技術，２０２０，４３（７）：６１－６６．

［１５］ 覃繼前，徐寧輝，梁月吉． 不同衛星高度角對ＧＰＳ ／ＧＬＯＮＡＳＳ ／ ＢＤＳ ／ Ｇａｌｉｌｅｏ 融合定位的影響［Ｊ］． 全球定位系統，２０２１，４６（２）：６２－６８．

［１６］ 劉建． 復雜環境下的衛星導航選星算法［Ｊ］． 無線電工程，２０１１，４１（７）：３９－４１．

［１７］ 朱軍，許士杰，李凱． 基于幾何分布和差分進化的雙模導航選星算法［Ｊ］． 北京郵電大學學報，２０２１，４４（３）：９－１４．

［１８］ 豐澤斌，馬龍華，朱國杰． 導航定位過程中的一種高效衛星組合選取策略［Ｊ］． 航天控制，２０１８，３６（３）：１５－２０．

［１９］ ＺＨＡＮＧ Ｍ Ｙ，ＺＨＡＮＧ Ｊ． Ａ Ｆａｓｔ Ｓａｔｅｌｌｉｔｅ Ｓｅｌｅｃｔｉｏｎ Ａｌｇｏｒｉｔｈｍ：Ｂｅｙｏｎｄ Ｆｏｕｒ Ｓａｔｅｌｌｉｔｅｓ［Ｊ］． ＩＥＥＥ Ｊｏｕｒｎａｌ ｏｆ ＳｅｌｅｃｔｅｄＴｏｐｉｃｓ ｉｎ Ｓｉｇｎａｌ Ｐｒｏｃｅｓｓｉｎｇ，２００９，３（５）：７４０－７４７．

作者簡介

王曉君 男，（１９７３—），博士，教授，碩士生導師。主要研究方向：衛星導航及其關鍵技術、實時信號處理算法設計與工程實現。

（*通信作者）黃婧如 女，（１９９９—），碩士研究生。主要研究方向：衛星導航及其關鍵技術、信號處理。

姚 遠 男，（１９９６—），碩士。主要研究方向：衛星導航及其關鍵技術。

劉昊昱 女，（１９７１—），碩士，高級工程師。

基金項目：河北省省級科技計劃項目———新一代電子信息技術創新專項（２１３１０４０２Ｄ）