巧借問(wèn)題情境 落實(shí)“三會(huì)”目標(biāo)

［摘 要］ 數(shù)學(xué)教學(xué)不僅要讓學(xué)生獲得知識(shí)，更重要的是要讓學(xué)生獲得數(shù)學(xué)學(xué)習(xí)能力、掌握數(shù)學(xué)研究方法. 在數(shù)學(xué)教學(xué)中，為了促進(jìn)“三會(huì)”目標(biāo)的達(dá)成，教師應(yīng)結(jié)合教學(xué)內(nèi)容創(chuàng)設(shè)有效的問(wèn)題情境，引導(dǎo)學(xué)生經(jīng)歷生活經(jīng)驗(yàn)數(shù)學(xué)化和數(shù)學(xué)問(wèn)題生活化的過(guò)程，以此激發(fā)學(xué)生的學(xué)習(xí)熱情，提高學(xué)生的應(yīng)用能力，落實(shí)數(shù)學(xué)學(xué)科核心素養(yǎng).

［關(guān)鍵詞］ 三會(huì)；問(wèn)題情境；數(shù)學(xué)學(xué)科核心素養(yǎng)

新課標(biāo)強(qiáng)調(diào)，數(shù)學(xué)教育引導(dǎo)學(xué)生會(huì)用數(shù)學(xué)眼光觀察世界，會(huì)用數(shù)學(xué)思維思考世界，會(huì)用數(shù)學(xué)語(yǔ)言表達(dá)世界，讓學(xué)生在問(wèn)題發(fā)現(xiàn)、探索、解決和表達(dá)過(guò)程中逐步提高發(fā)現(xiàn)、提出、分析和解決問(wèn)題的能力，讓學(xué)生學(xué)會(huì)學(xué)習(xí). 在教學(xué)中，教師要結(jié)合教學(xué)實(shí)際創(chuàng)設(shè)有效的教學(xué)情境，使學(xué)生以“發(fā)現(xiàn)者”“探究者”“參與者”“創(chuàng)造者”的身份融于數(shù)學(xué)課堂，讓學(xué)生通過(guò)獨(dú)立思考和合作交流逐步把握數(shù)學(xué)內(nèi)容的本質(zhì)，提高課堂教學(xué)有效性.

借助生活經(jīng)驗(yàn)，讓學(xué)生用數(shù)學(xué)眼光看待問(wèn)題

數(shù)學(xué)源于生活，又高于生活. 在數(shù)學(xué)教學(xué)中，教師要結(jié)合教學(xué)內(nèi)容引入一些學(xué)生熟悉的、感興趣的生活情境，以此有效溝通數(shù)學(xué)與生活的聯(lián)系，讓學(xué)生體會(huì)數(shù)學(xué)內(nèi)容的本質(zhì)，提高學(xué)生數(shù)學(xué)抽象、直觀想象等素養(yǎng).

例1 探尋“基本不等式”.

在本課教學(xué)中，教師不妨創(chuàng)設(shè)有效的問(wèn)題情境引導(dǎo)學(xué)生親歷知識(shí)形成的過(guò)程，促進(jìn)學(xué)生認(rèn)知體系的建構(gòu)和數(shù)學(xué)學(xué)科核心素養(yǎng)的落實(shí).

教師可以引入這樣一個(gè)情境問(wèn)題：已知b克糖水中含有a克糖（b>a>0），如果往糖水中繼續(xù)添加m克糖，糖水會(huì)發(fā)生怎樣的變化？問(wèn)題給出后，學(xué)生結(jié)合生活經(jīng)驗(yàn)很容易得到“糖水變甜了”這一結(jié)論. 在此基礎(chǔ)上，教師引導(dǎo)學(xué)生順勢(shì)思考：在這個(gè)現(xiàn)實(shí)生活情境中，你是否發(fā)現(xiàn)了數(shù)學(xué)的身影？你能用一個(gè)數(shù)學(xué)式子來(lái)表達(dá)蘊(yùn)含其中的數(shù)量關(guān)系并證明它嗎？在問(wèn)題的引導(dǎo)下，學(xué)生容易提煉出不等式<（b>a>0，m>0）. 通過(guò)經(jīng)歷上述過(guò)程，既為抽象的數(shù)學(xué)式子賦予了鮮活的生命力，又讓學(xué)生體會(huì)到了數(shù)學(xué)的抽象美、簡(jiǎn)約美.

其實(shí)，上述問(wèn)題情境的價(jià)值遠(yuǎn)不止于此，在此基礎(chǔ)上可以進(jìn)一步拓展. 例如，教師可以引導(dǎo)學(xué)生思考下列問(wèn)題.

①若將3杯甜度相同的糖水混合在一起，糖水會(huì)變甜嗎？如何用數(shù)學(xué)式子來(lái)表達(dá)？

②若將2杯甜度不同的糖水混合在一起，糖水甜度會(huì)如何變化？用數(shù)學(xué)式子又該如何表達(dá)？

③將2杯甜度不同的糖水混合在一起，糖水的混合濃度與其平均濃度相比，是怎樣的數(shù)量關(guān)系？

對(duì)于問(wèn)題①和問(wèn)題②，學(xué)生結(jié)合生活經(jīng)驗(yàn)?zāi)苤苯咏o出答案“===（其中a<b，i=1，2，3）”和“<?<<（其中a<b，i=1，2）”. 而對(duì)于問(wèn)題③，是挑戰(zhàn)性結(jié)論——比較

+

與（其中a<b，i=1，2）的大小.

這樣從學(xué)生熟悉的問(wèn)題情境出發(fā)，通過(guò)對(duì)問(wèn)題拓展延伸，不僅能拓寬學(xué)生的視野，還能幫助學(xué)生更好地理解數(shù)學(xué)知識(shí)，讓數(shù)學(xué)課堂更具生機(jī)和活力.

關(guān)注數(shù)學(xué)理解，讓學(xué)生用數(shù)學(xué)語(yǔ)言表達(dá)現(xiàn)實(shí)問(wèn)題

數(shù)學(xué)是一種抽象的思維活動(dòng)，為了讓學(xué)生更好地理解數(shù)學(xué)知識(shí)，教師要引導(dǎo)學(xué)生用數(shù)學(xué)語(yǔ)言表達(dá)生活實(shí)際問(wèn)題，以此通過(guò)加強(qiáng)數(shù)學(xué)語(yǔ)言與生活實(shí)際的聯(lián)系，來(lái)提高學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng)，發(fā)展學(xué)生的數(shù)學(xué)能力.

例2 認(rèn)真分析以下三件事，說(shuō)一說(shuō)它們分別與圖1中的哪個(gè)圖象的吻合度最高？剩下的一個(gè)圖象，你能否用一件事來(lái)表述？

（1）周一早晨，我剛離開(kāi)家，發(fā)現(xiàn)胸卡落在了家里，于是我回家取好再上學(xué).

（2）我離開(kāi)家后一直勻速向?qū)W校行駛，不過(guò)中途遇到一個(gè)紅燈耽擱了一些時(shí)間.

（3）今天陽(yáng)光明媚，我騎著自己的愛(ài)車(chē)離開(kāi)家，緩緩加速，向公園行駛.

問(wèn)題給出后，學(xué)生結(jié)合現(xiàn)實(shí)情境很快給出了答案：第（1）件事與圖D對(duì)應(yīng)，第（2）件事與圖A對(duì)應(yīng)，第（3）件事與圖B對(duì)應(yīng). 接下來(lái)，學(xué)生給出許多精彩的事件來(lái)表達(dá)圖C. 例如，今天離開(kāi)家的時(shí)間較早，路上的時(shí)間比較充裕，我緩緩減速行駛，欣賞路上的美景.

例3 構(gòu)建一個(gè)問(wèn)題情境，使其中變量關(guān)系能用二次函數(shù)解析式y(tǒng)=ax2（a>0）來(lái)描述.

在教師的啟發(fā)和指導(dǎo)下，學(xué)生結(jié)合已有的學(xué)習(xí)經(jīng)驗(yàn)“還原”解析式，有的學(xué)生聯(lián)想到自由落體運(yùn)動(dòng)：物體自由落體的運(yùn)動(dòng)規(guī)律是h=gt2（下落高度h是下落時(shí)間t的函數(shù)）；有的學(xué)生聯(lián)想到直角三角形的面積：對(duì)于給定銳角A的Rt△ABC，令Rt△ABC的面積為S，角A與直角的夾邊長(zhǎng)為x，則S=x2tanA. 通過(guò)經(jīng)歷問(wèn)題情境的建構(gòu)過(guò)程，不僅加深學(xué)生對(duì)函數(shù)概念的理解，還增強(qiáng)學(xué)生的建模意識(shí).

這樣引導(dǎo)學(xué)生用圖形、數(shù)學(xué)表達(dá)式來(lái)刻畫(huà)現(xiàn)實(shí)問(wèn)題，通過(guò)經(jīng)歷數(shù)學(xué)語(yǔ)言的“抽象”與“還原”，引導(dǎo)學(xué)生學(xué)會(huì)用數(shù)學(xué)語(yǔ)言去表達(dá)現(xiàn)實(shí)問(wèn)題，以此提高學(xué)生的數(shù)學(xué)語(yǔ)言表達(dá)能力，提升學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng).

重視數(shù)學(xué)探究，讓學(xué)生用數(shù)學(xué)思維思考現(xiàn)實(shí)問(wèn)題

“用數(shù)學(xué)”是數(shù)學(xué)教學(xué)的起點(diǎn)和落腳點(diǎn)，教學(xué)中要激發(fā)學(xué)生用數(shù)學(xué)思維思考現(xiàn)實(shí)問(wèn)題，以通過(guò)“用數(shù)學(xué)”來(lái)感悟數(shù)學(xué)學(xué)習(xí)價(jià)值，調(diào)動(dòng)學(xué)習(xí)動(dòng)機(jī).

例4 如圖2所示，小島與海岸線(xiàn)最近的點(diǎn)P的距離是2 km，點(diǎn)P的正東方向12 km處有一小城鎮(zhèn).

（1）某人從小島出發(fā)，先是駕駛小船以3 km/h的速度到達(dá)岸邊，然后以5 km/h的速度步行到達(dá)城鎮(zhèn). t（單位：h）表示他從小島到城鎮(zhèn)的時(shí)間，x（單位：km）表示小船停靠處與點(diǎn)P的距離. 請(qǐng)將t表示為x的函數(shù)，并寫(xiě)出其定義域.

（2）若小船停靠處到點(diǎn)P的距離是4 km，則他從小島到城鎮(zhèn)需要多少時(shí)間？（精確到小時(shí)）

解題時(shí)可以引導(dǎo)學(xué)生將圖2抽象成圖3，以便學(xué)生用數(shù)學(xué)思維思考現(xiàn)實(shí)問(wèn)題. 設(shè)點(diǎn)A為城鎮(zhèn)，點(diǎn)B為小島，點(diǎn)C為小船停靠的位置. 將現(xiàn)實(shí)問(wèn)題抽象成數(shù)學(xué)問(wèn)題后，學(xué)生很容易寫(xiě)出函數(shù)t（x）=+（0≤x≤12）. 當(dāng)x=4時(shí)，t≈3（h）. 其實(shí)，對(duì)于該問(wèn)題的探究不能局限于此，在此基礎(chǔ)上，教師還可提出以下幾個(gè)問(wèn)題.

問(wèn)題1 當(dāng)船停靠在何處時(shí)，最省時(shí)？

學(xué)生通過(guò)思考、探索、交流，求導(dǎo)得t′（x）=-=. 由此可知，t（x）在區(qū)間

0，

內(nèi)單調(diào)遞減，在區(qū)間

，12

內(nèi)單調(diào)遞增，所以當(dāng)船停靠在距P點(diǎn)1.5 km處時(shí)，最省時(shí).

問(wèn)題2 如果步行速度和小船速度相同，均為3 km/h，此時(shí)函數(shù)t（x）=+（0≤x≤12）的最小值是什么？

若解題時(shí)從單純的函數(shù)性質(zhì)的角度去思考，對(duì)于大多數(shù)學(xué)生而言，存在一定難度. 但是將其融于實(shí)際背景，問(wèn)題就簡(jiǎn)單了許多. 觀察圖象，通過(guò)思考可知，上述問(wèn)題的幾何意義為（BC+CA）≥BA，即當(dāng)x=12時(shí)，函數(shù)t（x）=+取最小值. 當(dāng)然，對(duì)于這一結(jié)論要用復(fù)合函數(shù)的單調(diào)性加以證明，這里不再贅述. 因此［t（x）］=t（12）=.

問(wèn)題3 你能根據(jù)問(wèn)題2的探究經(jīng)驗(yàn)，求出t（x）=+的最小值嗎？

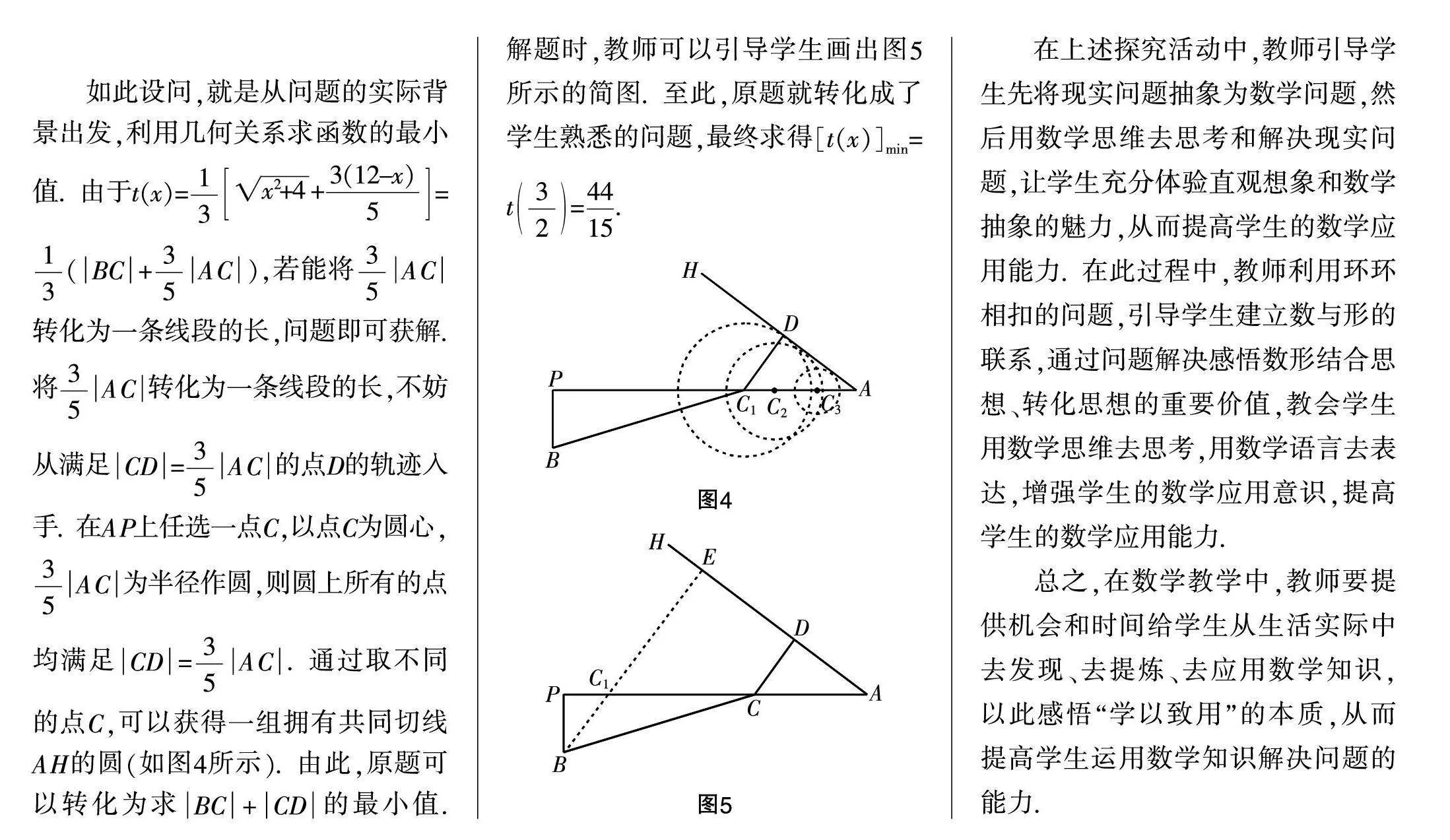
如此設(shè)問(wèn)，就是從問(wèn)題的實(shí)際背景出發(fā)，利用幾何關(guān)系求函數(shù)的最小值. 由于t（x）=

+=（BC+AC），若能將AC轉(zhuǎn)化為一條線(xiàn)段的長(zhǎng)，問(wèn)題即可獲解. 將AC轉(zhuǎn)化為一條線(xiàn)段的長(zhǎng)，不妨從滿(mǎn)足CD=AC的點(diǎn)D的軌跡入手. 在AP上任選一點(diǎn)C，以點(diǎn)C為圓心，AC為半徑作圓，則圓上所有的點(diǎn)均滿(mǎn)足CD=AC. 通過(guò)取不同的點(diǎn)C，可以獲得一組擁有共同切線(xiàn)AH的圓（如圖4所示）. 由此，原題可以轉(zhuǎn)化為求BC+CD的最小值. 解題時(shí)，教師可以引導(dǎo)學(xué)生畫(huà)出圖5所示的簡(jiǎn)圖. 至此，原題就轉(zhuǎn)化成了學(xué)生熟悉的問(wèn)題，最終求得［t（x）］=t

=.

在上述探究活動(dòng)中，教師引導(dǎo)學(xué)生先將現(xiàn)實(shí)問(wèn)題抽象為數(shù)學(xué)問(wèn)題，然后用數(shù)學(xué)思維去思考和解決現(xiàn)實(shí)問(wèn)題，讓學(xué)生充分體驗(yàn)直觀想象和數(shù)學(xué)抽象的魅力，從而提高學(xué)生的數(shù)學(xué)應(yīng)用能力. 在此過(guò)程中，教師利用環(huán)環(huán)相扣的問(wèn)題，引導(dǎo)學(xué)生建立數(shù)與形的聯(lián)系，通過(guò)問(wèn)題解決感悟數(shù)形結(jié)合思想、轉(zhuǎn)化思想的重要價(jià)值，教會(huì)學(xué)生用數(shù)學(xué)思維去思考，用數(shù)學(xué)語(yǔ)言去表達(dá)，增強(qiáng)學(xué)生的數(shù)學(xué)應(yīng)用意識(shí)，提高學(xué)生的數(shù)學(xué)應(yīng)用能力.

總之，在數(shù)學(xué)教學(xué)中，教師要提供機(jī)會(huì)和時(shí)間給學(xué)生從生活實(shí)際中去發(fā)現(xiàn)、去提煉、去應(yīng)用數(shù)學(xué)知識(shí)，以此感悟“學(xué)以致用”的本質(zhì)，從而提高學(xué)生運(yùn)用數(shù)學(xué)知識(shí)解決問(wèn)題的能力.