麻雀搜索算法-粒子群算法與快速擴展隨機樹算法協同優化的智能車輛路徑規劃

張志文 劉伯威 張繼園 唐杰 張天賜

摘要：

針對智能汽車在面對多樣化工作場景時其路徑規劃算法存在響應時間長、規劃效率低的問題，提出了多元協同優化策略。首先，融合麻雀搜索算法（SSA）的警惕機制與粒子群算法（PSO）的種群尋優特性，對PSO算法中的慣性權重因子和學習因子進行優化；其次，提出“三角布線”搜索規則，對快速擴展隨機樹算法（RRT）進行雙向優化（RRT-Connect）；然后，基于MATLAB軟件建立了復雜環境道路仿真模型，對上述優化方案進行了仿真驗證。結果表明，相較于單一的優化方案，協同優化算法在路徑長度與規劃時間上均具有顯著的優勢。對兩種協同優化方案的應用場景進行了實車試驗，結果顯示：在局部路徑規劃中，SSA-PSO算法響應時間更短，規劃效率更高，而在全局路徑規劃中，“三角布線”RRT-Connect算法更具優勢。

關鍵詞：路徑規劃；麻雀搜索算法；粒子群算法；三角布線；快速擴展隨機樹算法

中圖分類號：U461

DOI：10.3969/j.issn.1004132X.2024.06.005

開放科學（資源服務）標識碼（OSID）：

Cooperative Optimization of Intelligent Vehicle Path Planning Based on

PSO-SSA and RRT

ZHANG Zhiwen1，2? LIU Bowei3? ZHANG Jiyuan1? TANG Jie1? ZHANG Tianci1，2

1.School of Vehicle and Energy，Yanshan University，Qinhuangdao，Hebei，066004

2.Hebei Key Laboratory of Special Carrier Equipment，Yanshan University，Qinhuangdao，Hebei，066004

3.North Automatic Control Technology Institute，Taiyuan，030006

Abstract： Regarding the issues of long response time and low planning efficiency in the path planning algorithms for smart vehicles facing diverse working scenarios， a multi-element collaborative optimization strategy was proposed. Firstly， the vigilance mechanism of SSA was integrated with the population optimization characteristics of PSO， optimizing the inertia weight factor and learning factor in the PSO algorithm. Secondly， a “triangular wiring” search rule was introduced to perform bidirectional optimization（RRT-Connect） on the RRT algorithm. Subsequently， a complex environmental road simulation model was established using MATLAB software， and simulation tests were conducted on the proposed optimization solutions. The results demonstrate that， compared to single optimization approaches， the collaborative optimization algorithm exhibits significant advantages in terms of path length and planning time. Finally， real-vehicle tests are conducted on the application scenarios of the two collaborative optimization solutions， showing that in local path planning， the SSA-PSO algorithm has a shorter response time and higher planning efficiency， while in global path planning， the “triangular wiring” RRT-Connect algorithm exhibits greater advantages.

Key words： path planning；sparrow search algorithm（SSA）； particle swarm optimization（PSO） algorithm； triangular wiring； rapidly-exploring random tree（RRT） algorithm

收稿日期：20231013

基金項目：國家自然科學基金區域創新發展聯合基金（U20A20332）；國家自然科學基金（52175063）

0? 引言

工業4.0推動了機器人、智能產品、自動駕駛等領域的研究熱度［1］。自動駕駛技術標志著一個國家汽車工業發展水平，而我國已然成為智能車輛技術先進的國家。在智能汽車工作過程中，控制系統通過眾多傳感器采集到路況信息后，快速實時地規劃行駛路徑是自動駕駛關鍵技術之一，因此，路徑規劃算法的準確度和效率在一定程度上決定了智能車輛工作效率和工作質量。

對路徑規劃算法的研究有很多，常見的有A*算法［2］、遺傳算法［3］、神經網絡算法［4］、人工勢場法［5］、模擬退火算法［6］、蟻群算法［7］、RRT*算法［8］等。各種算法在不同領域中都有廣泛的應用，其優缺點也各不相同。CHENG等［9］提出多自適應度目標函數對路徑規劃結果進行評價，將最優路徑求解問題轉化為多目標優化問題。HAO等［10］將隨機種群分解為多個小型種群，種群之間的篩選機制由選擇算子更改為遷移機制，以適應多變的地圖環境。LAMINI等［11］提出了考慮距離和安全性能的交叉算子路徑規劃方法，給出了新的適應度函數，有效解決了早熟收斂的問題，達到了尋找最優路徑的目的。呂剛等［12］提出了一種結合A*算法和強化學習中近端策略優化算法的動態路徑規劃算法，通過縮短訓練周期避免算法過早陷入局部最優。彭曉燕等［13］提出離散優化的局部路徑規劃算法，引入代價函數評估候選路徑的安全性、平滑性，以獲得局部最佳路徑。徐釗等［14］通過分析人工勢場法、模糊邏輯算法和蟻群算法，提出一種增加垂直引導斥力來解決陷入局部最小值問題的方法。

麻雀搜索算法-粒子群算法與快速擴展隨機樹算法協同優化的智能車輛路徑規劃——張志文? 劉伯威? 張繼園等

中國機械工程 第35卷 第6期 2024年6月

本文基于麻雀搜索算法（sparrow search algorithm ，SSA）和粒子群優化（particle swarm optimization ，PSO）算法探索智能車輛避障與優化。 將麻雀搜索算法的學習因子和慣性權重因子引入到粒子群算法中進行優化，實現智能汽車局部路徑規劃。基于三角不等式函數改進快速搜索隨機樹（rapidly-exploring random tree ，RRT）算法，利用三角不等式原理，從函數角度解決最優性的局限問題，從而探索全局路徑規劃。

1? 路徑規劃

路徑規劃是智能汽車的關鍵技術，因此需要優異的算法以實現智能汽車更安全、更精準、更平滑地抵達目的地［15］。具體的路徑規劃研究要實現以下目標：安全到達目的地；計算時間短；路徑平滑且距離短；不能穿過障礙物或與障礙物發生碰撞。

本文提出的SSA-PSO算法將麻雀搜索算法和粒子群優化算法融合，選取各自的優點，使得智能汽車能夠勝任更多復雜場景的任務。同時受到三角不等式函數的啟發，采用基于“三角布線”的RRT-Connect算法以更好地適應不同的任務環境。搭建的智能汽車平臺在校園道路進行試驗，路況相對簡單，障礙物分布相對固定，突發情況較少，如圖1所示。

2? 融合麻雀搜索策略的粒子群優化算法

將麻雀搜索算法的速度更新方式和權重因子引入到粒子群算法中，通過調整參數提高SSA-PSO算法的收斂速度和搜索精度［16］。智能汽車采用PSO算法進行路徑規劃時，將每個粒子個體看作單獨的規劃路徑，若粒子群有n個粒子，則有n條路徑，將單個粒子中染色體個數m定義為中間過渡點數，而每個點又包含兩個維度（x，y）［17］，對粒子群進行迭代以選擇出合適個體，即最優路徑。

2.1? 算法模型建立

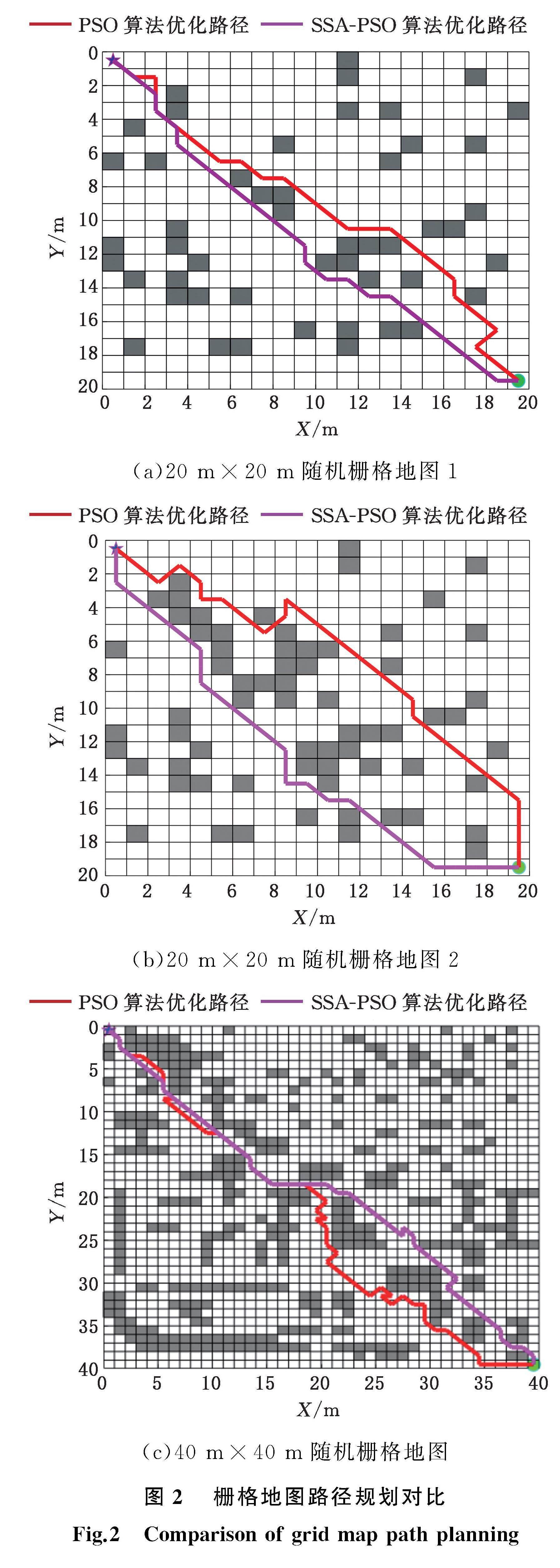
SSA-PSO算法在PSO基礎上進行SSA算法中速度的更新和位置的更新。為了在復雜函數尋優過程中避免迭代過程中漏掉實際最優，同時避免在更新位置后陷入局部最優，權重因子采用正弦變化，改進后的SSA-PSO算法權重因子為

ω（k）=ωmax－ωminksin（πkkmax）+ωmax+ωmink（1）

式中，ω（k）為第k次迭代的慣性權重因子，ωmax=1，ωmin=0.5；k為當前算法的迭代次數；kmax為最大迭代次數。

2.1.1? 位置更新原則

傳統粒子群優化算法經過麻雀搜索算法優化后，對其位置進行更新，公式如下：

Xid=Xid0+X（t+1）i，j（2）

式中，Xid為個體發生變化后的位置；Xid0為個體原始位置；X（t+1）i，j為第t+1代時麻雀的坐標信息。

每代位置更新公式定義如下：

X（t+1）i，j=X（t）i，jexp（－iaTmax）? A

X（t）i，j+QLA≥S（3）

式中，Tmax為最大迭代次數；X（t）i，j為第t代第i個麻雀在第j維中的位置信息；a為（0，1］的隨機數；A為警惕值，A∈［0，1］；S為安全閾值，S∈［0.5，0.7］；Q為服從正態分布的一個隨機數；L為一個1×d的矩陣，且元素均為1。

當A＜S時，表示附近無危險，麻雀可以在該空間范圍內隨意搜索食物；當A≥S時，表明發現者感知到危險，此時部分麻雀會以跟隨者的身份跟隨發現者一起行動，一旦發現者找到食物就會靠近與其爭奪食物，其中跟隨者中的一小部分因為食物太少就會飛到其他區域尋找食物。即跟隨過程中位置更新公式為

X（t+1）i，j=Qexp（X（t）w－X（t）i，ji2）??? ???i>N/2

X（t+1）P+|X（t）i，j－X（t+1）P|A+Li≤N/2（4）

式中，XP為目前發現者所占據的最優位置；Xw為當前全局最差的位置；N為種群數；A為一個1×d的矩陣，A+=AT（AAT）-1。

當i >N/2時，表明適應度值較低的第i個跟蹤者沒有得到食物，更換位置以獲取食物。當感知到危險時，麻雀種群會做出反捕食行為。即感知危險后位置要更新，其數學表達式如下：

X（t+1）i，j=X（t）B+b（X（t）i，j－X（t）B）??? fi≠fg

X（t）i，j+K（X（t）i，j－X（t）w|fi－fw|+ε）fi=fg（5）

式中，XB為當前的全局最優位置；b為步長調節因子；K為分布在［-1，1］的隨機數；fi為當前個體的適應度值；fg、fw分別為全局最佳和最差適應度值；ε為一個極小常數。

2.1.2? 速度更新原則

為了減少粒子群中粒子的隨機性，提高粒子運動的可控性，在位置更新過程中，粒子群算法優化過程中速度更新公式如下：

vid=ω（k）vid+c1r1（pid－xid）+c2r2（pgd－xid）（6）

式中，ω（k）為更新算法的慣性權重因子，根據工況確定ω的大小以平衡算法收斂性與全局搜索能力；r1、r2均為隨機值；vid為優化過后的SSA-PSO個體速度；pid為當前個體的最優位置；pgd為當前個體的全局最優位置；c1、c2為新的學習因子。

2.1.3? 碰撞檢查

路徑規劃后，用iscoll（·）函數檢查每段路徑是否和障礙物相交。原理如下：將障礙物輪廓投影到規劃路徑曲線上，將曲線段橫坐標n等分后取點，n的大小由障礙物輪廓大小及規劃路徑曲線的曲率確定，將每個點的坐標輸入到障礙物的邊界匿名函數中，以判斷該點是否落在障礙物中。若至少有一點落在障礙物上，說明路徑與障礙物發生了碰撞，則該路徑方案被否定。

2.2? 仿真實現及分析

基于MATLAB 平臺建立3種不同規格的柵格地圖，對傳統PSO和SSA-PSO算法進行仿真對比研究。以室內障礙物和常見的城市道路環境為基礎建立柵格環境［18］，為了驗證在任一隨機環境中具有普適性，在20 m×20 m的柵格地圖上路徑仿真結果對比見圖2a、圖2b，在40 m×40 m的柵格地圖上的結果對比見圖2c。表1為仿真圖路徑對比數據。由圖2可以看到，無論是小地圖（20 m×20 m）還是大地圖（40 m×40 m），SSA-PSO算法相比于PSO算法路徑規劃距離更短，效率更高。仿真結果表明：PSO算法與SSA-PSO算法規劃的路徑軌跡不同，SSA-PSO算法相較于PSO算法在以上三種地圖中最優路徑距離分別減少了7%、10%和14%。

3? 基于“三角布線”的RRT算法的路徑規劃

3.1? 數學模型建立

基于二維歐氏空間建立RRT-Connect算法的數學模型［19］，定義RRT算法中任意節點qi與其父節點ξ（qi）之間的路徑長度D（qi，ξ（qi））為

D（qi，ξ（qi））=（xξ（qi）-xqi）2+（yξ（qi）－yqi）2（7）

任意節點qi的第n個祖節點與第n + 1個祖節點之間的距離dn（qi）［20］為

dn（qi）=D（ξn（qi），ξn+1（qi））（8）

其中，qi是指插入的第i個任意節點，以該節點的x、y坐標值作為元素，ξ（qi）為qi節點的父節點函數，任意節點的第n個祖節點與其之間的距離用ξ的冪函數表示：

ξn（qi）=（ξξ…ξn）（qi）

其中，“”表示矩陣的哈達瑪（Hadamard）積，代表兩個映射構成復合映射。當n=0時，ξn（qi）=qi。

設起始位置為qstart，目標位置為qgoal，則當qgoal的第δ + 1個祖節點為qstart時即ξδ+1（qgoal）=qstart時路徑長度DR為相鄰節點距離之和，為

DR=∑δn=0dn（qgoal）（9）

圖3顯示了“三角布線”法的過程［21］。如圖3a所示，若qchild的父節點為qparent，則qparent的父節點為qancestor。qancestor是qchild的第二個祖節點，可以表示為

qancestor=ξ（qparent）=ξ2（qchild）（10）

圖3b為重新布線圖，此時結果為圖3c，其中α為qchild與qparent之間的距離，

β為qparent與qancestor之間的距離，γ為qchild與qancestor之間的距離，三角不等式原理可表示為

α+β≥γ（11）

qchild與qancestor之間的距離關系為

D（qchild，ξ（qchild））=α

D（ξ（qchild），ξ2（qchild））=β

D（qchild，ξ2（qchild））=γ（12）

D（qchild，ξ（qchild））+D（ξ（qchild），ξ2（qchild））≥

D（qchild，ξ2（qchild））（13）

式（12）、式（13）表明，采用“三角布線”法的RRT算法所規劃的路徑總是更短或等于原RRT算法所規劃的路徑。

任意路徑（起始位置為qstart，目標位置為qgoal）“三角布線”的路徑長度UR為

UR=∑nj=0ukj（qgoal）（14）

其中，kj表示UR的序列指標，其表達式為

kj=τj+k′j? k′j=0??? j=0

kj－1+1j≥1（15）

τj代表第j時間段內發生重接線的次數，ukj（qi）=D（ξk′j（qi），ξkj+1（qi）），非“三角布線”法的路徑長度DR為

DR=∑δn=0dn（qgoal）=∑nj=0∑kjn=k′jdn（qgoal）（16）

由于DR≥UR，因此“三角布線”法任意路徑的距離至少是相等的。

圖4顯示了“三角布線”的應用，體現了對RRT-Connect算法的“擴展”過程。在從Ta擴展到Tb的過程中，qstart 、qnewA、qnewB、qnear、qgoal 依次被重連，通過依次“三角布線”方式大幅度縮短路徑規劃距離。

3.2? 仿真分析

為了驗證RRT-Connect算法性能，通過仿真將RRT、RRT-Connect和“三角布線”RRT-Connect三種算法在試驗環境中進行對比研究。構建圖5所示的復雜環境地圖并仿真每個算法在地圖中的路徑規劃結果。仿真結果顯示，圖 5a的樣本數量最多，圖5b與圖5c算法的樣本數量相似，“三角布線”RRT-Connect算法路徑長度最短。

表2所示為每種算法的路徑規劃結果（重復試驗50次后）。RRT-Connect算法的平均樣本數量相對比率（基于RRT算法）最小，為72%；“三角布線”RRT-Connect算法的平均樣本數量相對比率（基于RRT算法）為73%，比RRT-Connect算法的效率低1%；“三角布線”RRT-Connect算法的平均路徑長度最短，為RRT算法的77%，RRT-Connect算法的平均路徑長度相對比率（基于RRT算法）為97%；RRT-Connect算法的平均規劃時間最短，為RRT算法的35%，“三角布線”RRT-Connect算法的規劃時間最短，比RRT算法的效率低1%。

4? 智能車輛路徑規劃平臺試驗

4.1? 試驗平臺硬件配置

為了保證智能車輛的路徑規劃研究具有實際可行性，選用基于激光雷達和毫米波雷達傳感器為主的純電動智能車輛試驗平臺開展試驗研究。在實車驗證時，局部路徑規劃采用SSA-PSO算法，全局路徑規劃采用基于“三角布線”的RRT-Connect算法。純電動無人駕駛智能車輛如圖6所示。

4.2? 路徑規劃驗證結果分析

基于純電動無人駕駛智能車輛平臺進行路徑規劃算法測試。圖7為試驗車系統結構圖，主要包括環境感知系統、規劃決策系統及底層控制系統。圖8所示為道路圖像采集過程，激光雷達采集點云信號，探測近距離復雜路況信息，毫米波雷達采集遠距離障礙物信息，ZED雙目相機采集路況的圖像信息。圖9為點云數據信號圖，高精度試驗過程中圖像識別系統通過各傳感器采集路況信息，圖像處理系統將圖像信息與點云信號進行信息融合。路徑規劃系統根據圖像處理后的數據建立包括障礙物信息的試驗路況。

測試過程中，首先將生成軌跡路徑與期望路徑數據進行對比分析；然后，測試車速變化情況，對比分析通過軟件仿真的預描車速、采用路徑規劃的速度及車輛行駛的實際數據；最后分析車輛遇到障礙物時偏離期望路徑的誤差。

選擇圖8路況進行測試，測試速度范圍為0～15 km/h，測試結果如圖10所示。其中圖10a用來對比路徑情況，結果顯示，在行駛的300 s內智能小車在0～15 km/h之間不斷加減速運行，實際行駛路徑和算法規劃路徑十分接近，即兩種優化算法規劃的路徑與實際路徑完全一致，表明算法規劃路徑準確性較高。圖10b用來對比車速變化情況，結果顯示，在16 s之前智能小車未遇到新的障礙物，處于不斷加速狀態，在16 s后障礙物出現，智能小車進行實時減速避障，采用SSA-PSO算法進行了局部路徑規劃，算法規劃的速度優于實際速度，證明提出的算法在應對該工況時規劃效率較高。圖10c用來作橫向誤差對比，結果顯示，提出的算法在該路況下，行駛時發生的橫向誤差基本在-0.1～0.1 m之間，證明算法在遇到障礙物時偏離期望路徑的誤差較小，算法精度較高。

表3所示為工況試驗結果數據，智能車輛在局部規劃時，SSA-PSO算法需要62 ms，而基于“三角布線”的RRT-Connect算法需要69 ms，SSA-PSO算法相較于基于“三角布線”的RRT-Connect算法規劃時間要少7 ms，表明了在試驗工況中智能車輛局部路徑規劃時SSA-PSO算法表現更好，效率更高，性能更優。然而，在智能車輛全局規劃時，SSA-PSO算法需要141 ms，基于“三角布線”的RRT-Connect算法僅需要122 ms，基于“三角布線”的RRT-Connect算法相較于SSA-PSO算法規劃時間要少19 ms，表明在試驗工況中智能車輛全局路徑規劃時基于“三角布線”RRT-Connect算法表現更好，效率更高，性能更優。

5? 結論

（1）對智能車輛路徑規劃的算法進行了優化，通過將麻雀搜索算法（SSA）的警惕機制與粒子群優化（PSO）算法的種群尋優特性相結合，并對PSO算法中的慣性權重因子、學習因子進行優化，可在加強算法局部搜索能力的同時，保持種群的多樣性，防止算法在快速收斂的同時出現早熟。

（2）基于三角不等式原理融合隨機樹算法探索全局路徑規劃，利用三角不等式原理解決最優性的局限問題，基于“三角布線”法優化RRT-Connect算法提高全局路徑優化精度與效率。

（3）基于純電動無人駕駛智能車輛試驗平臺對提出的算法進行了試驗驗證，結果表明兩種優化算法均具有高效性與精確性。

參考文獻：

［1］? SCHWAB K. The Fourth Industrial Revolution［M］. New York：Crown Business， 2017.

［2］? 張鵬. 基于改進A*算法的全局動態路徑規劃研究［D］.太原：中北大學，2021.

ZHANG Peng. Research on Global Dynamic Path Planning Based on Improved A* Algorithm［D］. Taiyuan：North University of China， 2021.

［3］? GILBERT E G， JOHNSON D W. Distance Functions and Their Application to Robot Path Planning in the Presence of Obstacles［J］. IEEE Journal on Robotics and Automation ，1985， 1（1）：21-30.

［4］? MADANI T， DAACHI B， BENALLEGUE A. Adaptive Variable Structure Controller of Redundant Robots with Mobile/Fixed Obstacles Avoidance［J］. Robotics and Autonomous Systems， 2013，61（6）：555-564.

［5］? LI G， TONG S， CONG F， et al. Improved Artificial Potential Field-based Simultaneous Forward Search Method for Robot Path Planning in Complex Environment［C］∥2015 IEEE/SICE International Symposium on System Integration. Nagoya ：IEEE，2015：760-765.

［6］? 夏軍勇， 劉科進， 鐘飛， 等. 運用改進的教學模擬退火算法辨識關節臂式三坐標測量機的結構參數［J］. 中國機械工程， 2023， 34（3）：314-323.

XIA Junyong， LIU Kejin， ZHONG Fei，et al. Structural Parameter Identification for Articulated Arm Coordinate Measuring Machines Using Modified Teaching-learning-based Optimization Optimized by Simulated Annealing Algorithm［J］. China Mechanical Engineering， 2023， 34（3）：314-323.

［7］? 劉加奇，王泰華，董征. 基于改進蟻群算法的移動機器人路徑規劃［J］.傳感器與微系統，2022，41（5）：140-143.

LIU Jiaqi， WANG Taihua， DONG Zheng. Path Planning of Mobile Robot Based on Improved Ant Colony Algorithm［J］. Sensors and Microsystems，2022，41（5） ：140-143.

［8］? 師穎慧，張冰，趙強. 改進型RRT*算法的水下機器人三維全局路徑規劃［J］.軟件導刊， 2022，21（2）：48-52.

SHI Yinghui，ZHANG Bing， ZHAO Qiang. 3D Global Path Planning of Underwater Vehicle Based on Improved RRT* Algorithm［J］. Journal of Software Guide， 202，21（2）：48-52.

［9］? CHENG K P， RAJESH? E M， NGUYEN H K N，et al. Multi-objective Genetic Algorithm Based Autonomous Path Planning for Hinged Tetro Reconfigurable Tiling Robot［J］. IEEE Access，2020，8：121267-121284.

［10］? HAO K， ZHAO J L， YU K C， et al. Path Planning of Mobile Robots Based on a Multi-population Migration Genetic Algorithm［J］. Sensors， 2020，20（20）：5873-5873.

［11］? LAMINI C， BENHLIMA S， ELBEKRI A. Genetic Algorithm Based Approach for Autonomous Mobile Robot Path Planning［J］. Procedia Computer Science，2018，127：180-189.

［12］? 呂剛，呂金壯，鄧軍，等. 部分環境信息未知下的機器人動態路徑規劃算法［J］.自動化與儀器儀表， 2022（3）：186-190.

LYU Gang， LYU Jinzhuang， DENG Jun， et al. Robot Dynamic Path Planning Algorithm with Unknown Environmental Information［J］. Automation & Instrumentation， 2022（3）：186-190.

［13］? 彭曉燕，謝浩，黃晶. 無人駕駛汽車局部路徑規劃算法研究［J］.汽車工程， 2020，42（1）：1-10.

PENG Xiaoyan， XIE Hao， HUANG Jing. Research on Local Path Planning Algorithm for Driverless Vehicles［J］. Automotive Engineering， 2019，42（1）：1-10.

［14］? 徐釗，胡勁文，馬云紅，等. 無人機碰撞規避路徑規劃算法研究［J］.西北工業大學學報， 2019，37（1）：100-106.

XU Zhao， HU Jinwen， MA Yunhong， et al. Research on Collision Avoidance Path Planning Algorithm for UAV［J］. Journal of Northwestern Polytechnical University， 2019，37（1）：100-106.

［15］? AGARWAL D， BHARTI P S. Implementing Modified Swarm Intelligence Algorithm Based on Slime Moulds for Path Planning and Obstacle Avoidance Problem in Mobile Robots［J］. Applied Soft Computing Journal， 2021，107：233613844.

［16］? ZAFAR M N， MOHANTA J C. Methodology for Path Planning and Optimization of Mobile Robots：a Review［J］. Procedia Computer Science，2018，133：141-152.

［17］? 劉伯威. 基于改進PSO與RRT的智能車輛路徑規劃研究［D］.太原：中北大學，2023.

LIU Bowei. Research on Intelligent Vehicle Path Planning Based on Improved PSO and RRT［D］. Taiyuan：North University of China，2023.

［18］? 杜婉茹，王瀟茵，田濤，等. 面向未知環境及動態障礙的人工勢場路徑規劃算法［J］.計算機科學， 2021，48（2）：250-256.

DU Wanru， WANG Xiaoyin， TIAN Tao， et al. Artificial Potential Field Path Planning Algorithm for Unknown Environment and Dynamic Obstacles［J］. Computer Science， 2021，48（2）：250-256.

［19］? 李兆強，張時雨. 基于快速RRT算法的三維路徑規劃算法研究［J］.系統仿真學報， 2022，34（3）：503-511.

LI Zhaoqiang， ZHANG Shiyu. Research on 3D Path Planning Algorithm Based on Fast RRT Algorithm［J］. Journal of System Simulation， 2022，34（3）：503-511.

［20］? WANG Z F， WANG Q， BILL M， et al. Optimal Submarine Cable Path Planning and Trunk-and-Branch Tree Network Topology Design［J］. IEEE/ACM Transactions on Networking， 2020，28（4）：1562-1572.

［21］? JEONG I B， LEES J， KIM J H. Quick-RRT*：Triangular Inequality Based Implementation of RRT* with Improved Initial Solution and Convergence Rate［J］. Expert Systems with Applications， 2019，123（1）：82-90.

（編輯? 王艷麗）

作者簡介：

張志文，男，1984 年生，副教授。研究方向為新能源車輛能量管理、智能汽車路徑規劃。E-mail：zhzhw@ysu.edu.cn。

張天賜（通信作者），男， 1993年生，講師、博士研究生。研究方向為無人化工程車輛運動規劃、智能系統開發。E-mail：ztc@ysu.edu.cn。