基于PSO的電動汽車規模化充電接入配電網柔性負荷多目標優化控制

龐松嶺 范凱迪 竇潔 陳超

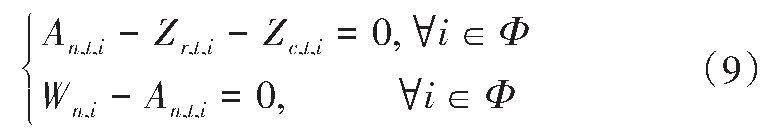
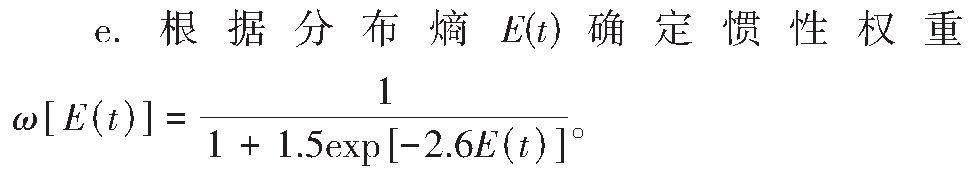
【摘要】為了降低電動汽車大規模接入配電網后產生的負荷波動和網損，提出了基于粒子群優化（PSO）算法的電動汽車規模化充電接入配電網柔性負荷多目標優化控制方法。首先，建立交通網-配電網耦合模型，并結合出行鏈模型分析用戶的充電需求，搭建接入電動汽車能量狀態預測模型；其次，以最小化配電網負荷波動標準差和網損作為優化目標，設計電動汽車規模化充電接入配電網柔性負荷多目標優化函數，同時引入分布熵設計慣性權重更新策略，優化PSO算法；最后，采用改進的PSO算法在函數約束條件的基礎上實現配電網的柔性負荷控制。測試結果表明，所提出的方法可準確分析用戶的充電需求，降低配電網負荷波動峰值及網損。

主題詞：電動汽車 粒子群優化算法 出行鏈模型 優化控制策略

中圖分類號：TM711? ?文獻標志碼：A? ?DOI： 10.19620/j.cnki.1000-3703.20230588

Multi-Objective Optimization Control of Flexible Loads for Large-Scale Charging of Electric Vehicles Connected to Distribution Networks Based on PSO

【Abstract】In order to reduce load fluctuations and network losses caused by large-scale electric vehicles connected to the distribution network， this paper proposed a multi-objective optimization control method based on Particle Swarm Optimization （PSO） algorithm for flexible loads of large-scale electric vehicle charging connected to the distribution network. Firstly， a coupling model between transportation network and distribution network was established， and combine it with the travel chain model to analyze users charging needs， and a prediction model for the energy state of connected electric vehicles was established; Secondly， the minimized standard deviation of load fluctuations and network losses in the distribution network was taken as the optimization objective， and a multi-objective optimization function was established for the flexible load integration of large-scale charging of electric vehicles into the distribution network， meanwhile distribution entropy was introduced to design inertia weight update strategy and optimize PSO algorithm. Finally， the improved PSO algorithm was used to achieve flexible load control of the distribution network based on functional constraints. The test results show that the proposed method can accurately analyze the charging needs of users， and reduce the peak load fluctuation and network loss of the controlled distribution network.

Key words： Electric vehicles， Particle Swarm Optimization （PSO） algorithm， Travel chain model， Optimize control strategies

1 前言

隨著電動汽車保有量的不斷增大，相應基礎充電設施大幅增加，配電網受電動汽車充電的影響和沖擊不斷加劇[1]。接入配電網的電動汽車是隨機性較高的移動負荷，易造成負荷波動峰值過高、網損增加和線路過載等問題[2-3]。為確保配電網的運行安全，需對規模化充電接入配電網的柔性負荷開展優化控制。

李景麗等[4]利用蒙特卡洛方法預測電動汽車接入配電網后的充電負荷，結合粒子群優化算法實現了配電網負荷的優化控制，但該方法無法準確預測用戶的充電需求，優化后配電網負荷波動仍較大。……