計數原理單元測試卷(A卷)

曲海勝

一、單選題（本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。）

1.從4名男生與3名女生中選2人去參加一場數學競賽，則男女生各1人的不同的選派方法數為（ ）。

A.7 B.12 C.18 D.24

2.2023年夏天貴州榕江的村超聯賽火爆全國，吸引了國內眾多業余球隊參賽。現有6個參賽隊伍代表站成一排照相，其中貴陽折耳根隊與柳州螺螄粉隊必須相鄰，同時南昌拌粉隊與溫江烤肉隊不能相鄰，那么不同的站法共有（ ）種。

A.144 B.72 C.36 D.24

3.已知C7n+1=C7n+C8n（n∈N* ），則n=（ ）。

A.14 B.15 C.13 D.12

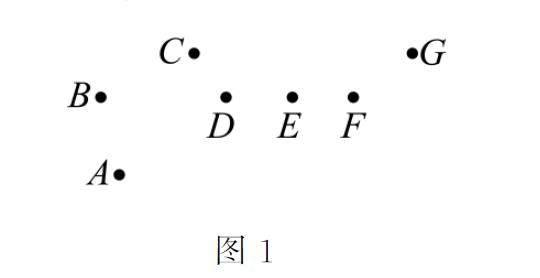
4.北斗七星是夜空中的七顆亮星，我國漢代緯書《春秋運斗樞》就有記載，它們組成的圖形像我國古代舀酒的斗，故命名北斗七星。北斗七星不僅是天上的星象，也是古人藉以判斷季節的依據之一。如圖1所示，用點A，B，C，D ，E，F，G 表示某一時期的北斗七星，其中B，D ，E，F 看作共線，其他任何3個點均不共線，過這7個點中任意2個點作直線，所得直線的條數為（ ）。

A.4 B.13 C.15 D.16

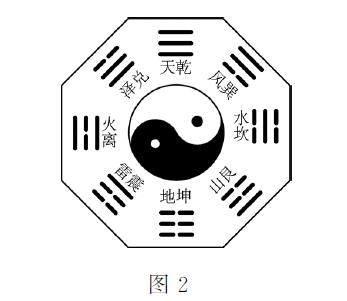
5.如圖2所示，古代中國的太極八卦圖是以同圓內的圓心為界，畫出形狀相同的兩個陰陽魚，陽魚的頭部有個陰眼，陰魚的頭部有個陽眼，表示萬物都在相互轉化，互相滲透，陰中有陽，陽中有陰，陰陽相合，相生相克，蘊含現代哲學中的矛盾對立統一規律。由八卦模型圖可抽象得到正八邊形，從該正八邊形的8個頂點中任意取出4個構成四邊形，其中梯形的個數為（ ）。

A.16 B.20 C.24 D.28

6.在（1-x2）（x-1／x）6的展開式中，含x2 項的系數是（ ）。

A.-20 B.5 C.15 D.35

7.某學校派出5名教師去3所鄉村學校支教，其中有一對教師夫婦參與支教活動。根據相關要求，每位教師只能去1所學校參與支教，并且每所學校至少有1名教師參與支教，同時要求這對教師夫婦必須去同所學校支教，則不同的安排方案有（ ）。

A.18種 B.24種

C.36種 D.48種

8.中國南北朝時期的著作《孫子算經》中，對同余除法有較深的研究，設a，b，m（m >0）均為整數，若a 和b 被m 除得的余數相同，則稱a 和b 對模m 同余，記為a≡b（modm）。如9 和21 被6 除得的余數都是3，則記9≡21（mod6）。若a≡b（mod10），且a=C0 20+C1 20·2+C2 20·22+…+C2200·220，則b 的值可以是（ ）。

A.2 019 B.2 020

C.2 021 D.2 022

二、多選題（本題共4小題，每小題5分，共20分。在每小題給出的選項中，有多項符合題目要求。全部選對的得5分，部分選對的得2分，有選錯的得0分。）

9.下列結論正確的是（ ）

（2）女生互不相鄰的坐法有多少種？

（3）甲、乙兩位同學相鄰且都不與丙同學相鄰的坐法有多少種？ （列出算式，并計算出結果）

18.（本小題12分）（1）解關于x 的不等式Ax8<6Ax8-2。

（2）求等式C5n-1+C3n-3／C3n-3 =195中n 的值。

19.（本小題12分）已知集合A={x|1

（1）從A∪B 中取出3個不同的元素組成三位數，則可以組成多少個？

（2）從集合A 中取出1個元素，從集合B 中取出3個元素，可以組成多少個無重復數字且比4 000大的正整數？

20.（本小題12分）已知（ax- 1／根號下x）n（a∈R，n∈N* ）的展開式的前三項的二項式系數之和為22，所有項的系數之和為1。

21.（本小題12分）用1，2，3，4，5，6這6個數字，可以組成多少個無重復數字的：

（1）四位偶數？

（2）數字1、3、5互不相鄰的六位數？

（3）六位數？ 其中數字6、4、1按自左至右的順序保持不變（如634 512，562 431）。

注：所有結果均用數值表示。

22.（本小題12分）已知（a-2x）8=a0+a1（x-1）+a2（x-1）2+…+a8（x-1）8，其中實數a>0，且x2 的系數為81 648。

（1）求實數a 的值。

（2）計算：（ⅰ）（a0+a2+a4+a6+a8）·（a1+a3+a5+a7）;

（ⅱ）|a0|+|a1|+|a2|+ … +|a8|。（結果用冪的形式表示）

（責任編輯 徐利杰）