聚焦基礎(chǔ)知識(shí) 考查關(guān)鍵能力

廖國(guó)達(dá)

2024年高考數(shù)學(xué)新課標(biāo)I卷（簡(jiǎn)稱(chēng)“新課標(biāo)I卷”）聚焦基礎(chǔ)知識(shí)的夯實(shí)，通過(guò)優(yōu)化題量、提升解答題分值和多選題賦分的方式，旨在更好地體現(xiàn)數(shù)學(xué)的本質(zhì)，強(qiáng)化對(duì)學(xué)生理性思維和應(yīng)用能力的考查。改革后的新課標(biāo)I卷旨在培養(yǎng)學(xué)生的核心素養(yǎng)，選拔具備創(chuàng)新精神的優(yōu)秀人才。試卷呈現(xiàn)出選擇和填空題整體難度適中、試題梯度設(shè)計(jì)合理、解答題具有一定的難度和區(qū)分度等特點(diǎn)。試卷著重考查學(xué)生的主干知識(shí)、能力和素養(yǎng)，突出思維過(guò)程、思維方法和創(chuàng)新能力，助力素質(zhì)教育和拔尖人才的選拔，充分體現(xiàn)了改革的理念和要求。

重視基礎(chǔ)，回歸課標(biāo)，突出數(shù)學(xué)教學(xué)本質(zhì)

1.重點(diǎn)考查主干知識(shí)

從具體的考查內(nèi)容來(lái)看，這份試卷重點(diǎn)考查主干知識(shí)，具體包括：函數(shù)與導(dǎo)數(shù)（第6、8、10、13、18題，共38分）、解析幾何（第11、12、16題，共26分）、立體幾何（第5、17題，共20分）、三角函數(shù)（第4、7、15題，共23分）、概率統(tǒng)計(jì)（第9、14題，共11分）、數(shù)列（第19題，17分）、集合（第1題，5分）、復(fù)數(shù)（第2題，5分）以及向量（第3題，5分）。

值得注意的是，雖然平時(shí)常考的知識(shí)點(diǎn)，如直線與圓、等比數(shù)列、二項(xiàng)式定理、統(tǒng)計(jì)、回歸方程、分布列等并未直接出現(xiàn)在試卷中，但不等式作為解決數(shù)學(xué)問(wèn)題的重要工具，被巧妙地融入了多個(gè)考題（第1、6、8、9、10、11、18題）之中，體現(xiàn)了其作為一條暗線的核心作用。這樣的設(shè)計(jì)不僅考查了學(xué)生對(duì)基礎(chǔ)知識(shí)的掌握，也檢驗(yàn)了他們的解題技巧和靈活應(yīng)用能力。

2.考查基礎(chǔ)知識(shí)，回歸教材

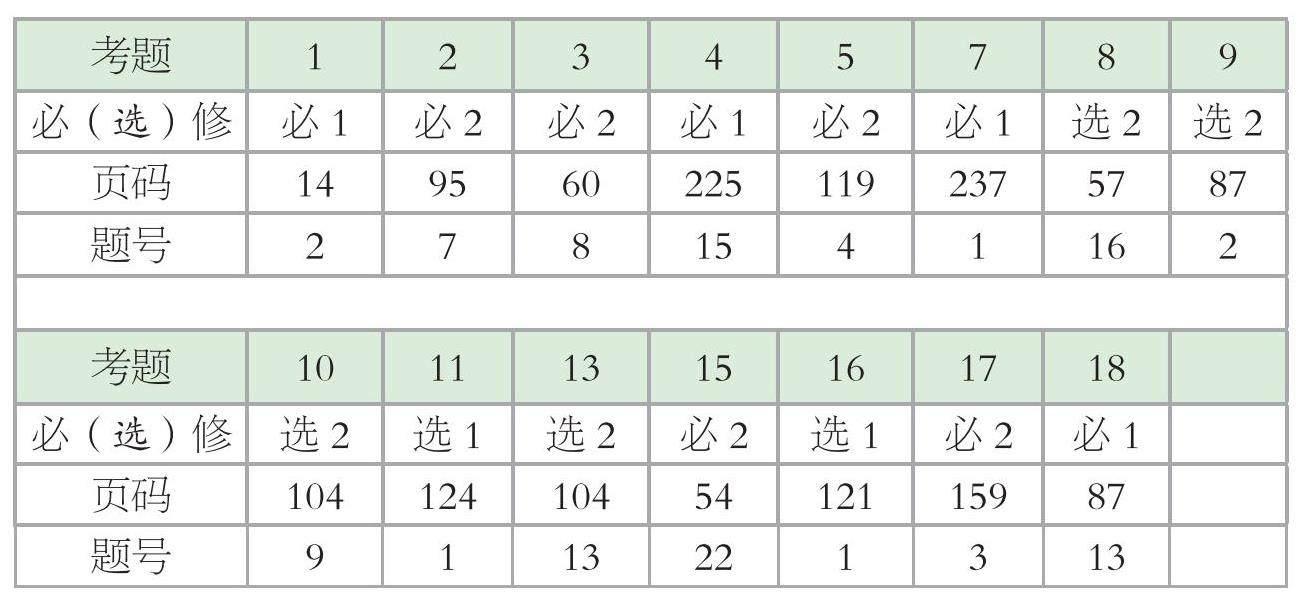
仔細(xì)審視試卷內(nèi)容，可以發(fā)現(xiàn)其仍然以考查基礎(chǔ)內(nèi)容為主導(dǎo)，多數(shù)題目的……