基于多組件圖神經網絡的多元序列因果推斷

張有興 李平 烏嶸 楊曉麗 李玉東 孟亮

DOI：10.16246/j.issn.1673-5072.2024.04.012

收稿日期：2023-03-15? 基金項目：國家自然科學基金項目（62276099）

作者簡介：張有興（1980—），男，高級工程師，主要從事天然氣勘探開發與人工智能研究。

通信作者：李平（1979—），女，教授，主要從事數據挖掘、智能油田技術研究。E-mail：pingkly@163.com

引文格式：張有興，李平，烏嶸，等.基于多組件圖神經網絡的多元序列因果推斷［J］.西華師范大學學報（自然科學版），2024，45（4）：430-437.［ZHANG Y X，LI P，WU R，et al.Causality inference for multivariate series based on multi-component graph neural network［J］.Journal of China West Normal University （Natural Sciences），2024，45（4）：430-437.］

摘? 要：圖神經網絡對非線性及高階交互作用具有強大的表征能力，提高了格蘭杰因果推斷的可解釋性和準確性。本文提出了一種基于多組件圖神經網絡的多元時間序列格蘭杰因果關系推斷方法（MCGNN），利用多組件圖卷積神經網絡分別獲取多元序列之間的非線性作用關系，同時引入門控循環單元對時間序列進行建模，將多元時間序列之間的因果關系問題轉化為時間序列之間的預測問題。在公開的模擬數據和真實數據集上的試驗結果表明，相比于當前已知最好的模型，MCGNN具有更高的準確性。特別地，將模型應用于天然氣深冷工藝數據集中，能夠動態發現深冷工藝中位點傳感器之間的因果關系，并與深冷工藝專家的判斷一致。

關鍵詞：格蘭杰因果；圖神經網絡；多元時間序列；非線性作用；高階交互作用

中圖分類號：TP391??? 文獻標志碼：A??? 文章編號：1673-5072（2024）04-0430-08

在多元時間序列數據挖掘任務中，解釋多元時間序列之間的相互作用關系是其重要組成部分，對理解數據挖掘結果具有重要意義。例如，在神經科學領域，研究人員試圖分析各個腦區活動的相互作用對后續腦區

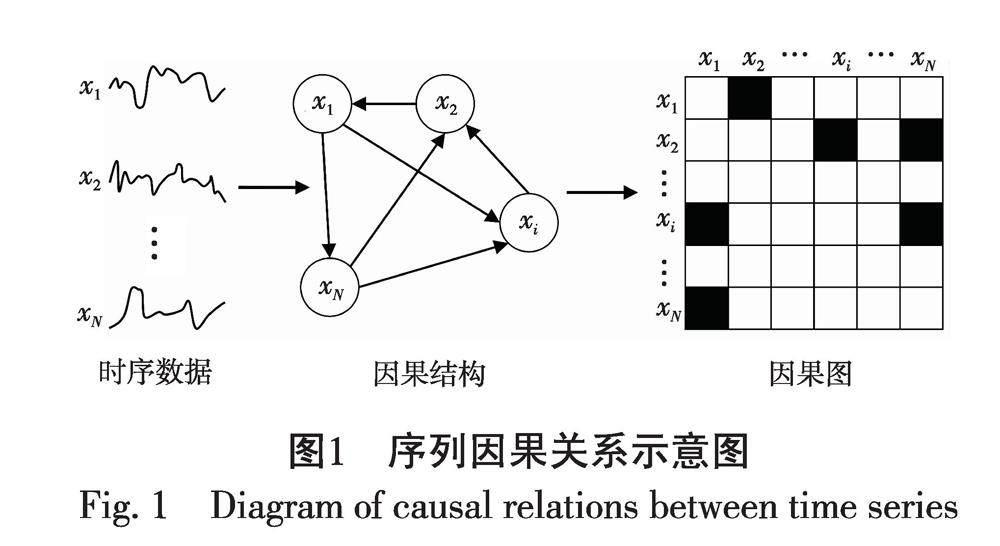
活動的影響［1-2］；在社交媒體分析中，了解各個話題之間的相互影響可以為信息傳播預測提供有力依據［3］；在基因組學中，探索基因表達的時間序列間的相互影響有助于推斷基因調控網絡的作用機制［4-5］。目前，格蘭杰因果［6］是理解時間序列間關系的常用框架。圖1描述了多元時間序列到因果圖的轉化過程，其中，因果結構中每個節點表示系統中的一個序列（變量），每條邊描述了兩個節點間的因果關系，且邊是有向的。

格蘭杰因果推斷方法大致可以分為兩類，一類是無模型的方法，另一類是基于模型的方法。無模型的方法能夠通過對預測關系的最小假設來檢測時間序列過去和未來之間的非線性依賴關系，如傳遞熵［7］、有向信息［8］等。然而，這種無模型的方法在進行可靠的因果關系估計時需要大量數據，同時這些方法難以應對高維數據，容易遭受維度災難。目前絕大多數的格蘭杰因果推理方法采用基于模型的推理方法，即：使用參數化生成模型對可觀測的時間序列數據進行建模，該模型的推斷參數用于反映格蘭杰因果關系的真實拓撲結構。早期的格蘭杰因果關系推理技術包括動態貝葉斯網絡［9］和具有時變系數的正則化邏輯回歸［10］等。然而，這些方法對于數據的非線性建模能力有限且只能推斷無向的因果關系。近年來，神經網絡因其在表示輸入與輸出之間復雜的非線性相互作用上展現出強大的特征表達能力而被廣泛用于推斷格蘭杰因果關系［11-13］。例如，Xu等［14］提出了一種可擴展因果圖學習網絡，該模型通過低秩逼近降低了噪聲的影響，并在模擬和真實數據集上實現了更好的精度和高擴展性。Marcinkevis等［15］將自解釋神經網絡［16］拓展到時間序列分析，提出了一種廣義向量自回歸模型，并通過稀疏誘導和時間平滑懲罰來找到時序數據中穩定的格蘭杰因果關系。

基于傳統神經網絡的模型雖然能有效推斷出多元時間序列間的因果關系，但是其解釋性較差。格蘭杰因果關系挖掘的挑戰是對于包含多元變量的系統而言，變量（即序列）間存在著未知且復雜的非線性關系。傳統的因果發現方法主要通過干預或現實生活中的實驗來操縱變量的值，同時控制目標變量的所有其他影響因素不變，以測試目標變量是否會隨著操作變量的變化而變化。其他方法如基于功能因果模型的因果發現算法［17］建立在非對稱獨立性假設基礎上，即因變量的分布與結果變量的分布條件獨立。

為提高因果關系推斷的準確性和可解釋性，本文提出了一種基于多組件圖神經網絡的多元時間序列格蘭杰因果關系推斷方法（Multi-Component Graph Neural Networks，MCGNN），該方法首次將圖神經網絡應用于格蘭杰因果推斷任務，使用圖卷積網絡（Graph Convolutional Network，GCN）［18］表征多元變量之間的可能關系，并結合門控循環單元（Gated Recurrent Unit，GRU）［19］捕捉單個變量的時變特征，提高推斷能力。此外，考慮到基于傳統神經網絡的因果推斷模型缺乏解釋能力，受文獻［20］的啟發，采用組件級模型架構，增強模型的可解釋性。最后，將MCGNN模型和其他基線模型在模擬數據集和真實數據集上進行對比實驗，并將該模型應用于實際天然氣生產工藝中。

1? 模? 型

1.1? 問題定義

多元時間序列間的格蘭杰因果關系通常由一組有向的依賴關系給出。例如，文獻［21］給出了格蘭杰因果關系的經典定義。本文根據Tank等［20］的拓展來定義非線性格蘭杰因果關系。若存在一組具有N個變量的時間序列X={x1，x2，…，xN}，假設變量之間的格蘭杰因果關系由以下結構方程模型給出。

第45卷第4期????? 張有興，等：基于多組件圖神經網絡的多元序列因果推斷

西華師范大學學報（自然科學版）http：∥igne.cbpt.cnki.net/2024年

x（t+1）（t+τ）j∶=fi（x（t+1）：（t+τ）1，…，x（t－l+1）：ti，…，x（t－l+1）：tN）+εtj，

式中：1jN，τ為溫度系數，x（t－l+1）：ti表示含有前l個時間步歷史信息的第i個變量，fi（·）是一個非線性函數，指定了變量xj的未來值如何依賴于X的過去值，而εtj是一個附加項。

多元序列之間的格蘭杰因果關系可以通過一個有向圖G=（V，E，A）進行概括［22］，其中V={x1，x2，…，xN}是時間序列對應的節點集合，E={（xi，xj）：xi→xj}表示存在格蘭杰因果關系的時間序列之間的連邊集合，A∈{0，1}N×N表示圖G的鄰接矩陣。因此，格蘭杰因果推斷任務是從多元時間序列的歷史觀測數據中發現內在的依賴關系來，從而實現對A的估計。

1.2? 模型總體架構

MCGNN的整體框架如圖2所示。具體來講，在因果推斷階段使用GCN和GRU網絡進行時間序列預測，自動學習每個目標變量的因果關系矩陣。再將因果關系矩陣送入到因果關系抽取階段，利用異常值檢測方法對生成的因果關系進行二元決策，從而得到序列間的格蘭杰因果關系。該方法主要包含因果關系推斷與因果關系抽取兩階段處理過程。在因果關系推斷過程中，利用多元時間序列X={x1，x2，…，xN}的歷史數據分別預測各個序列未來一段時間內的演變趨勢。在模型訓練過程中，通過減少預測誤差，學習時間序列之間的因果關系矩陣Ai，其中i=1，2，…，N。由于在反向傳播過程中，每一個變量的時間序列所學習到的因果關系矩陣Ai之間存在偏差，所以無法明確判斷出序列之間存在的關系是否為因果關系。因此，需要進一步對因果關系矩陣Ai進行因果關系抽取，得到可靠的序列間因果關系矩陣A。在因果關系抽取過程中，本文采用異常檢測中的離群點檢測方式來提取具體的格蘭杰因果關系圖A。總的來說，模型整體處理流程以多元時間序列X={x1，x2，…，xN}作為輸入，先經過多組件的因果關系推斷模塊得到因果關系推斷矩陣Ai，再將Ai送入到因果關系抽取模塊得到多元時間序列間的格蘭杰因果關系圖A。

1.3? 因果關系推斷

因果關系推斷階段的目的是通過多組件時間序列預測來學習各組件的多元序列之間的格蘭杰因果關系矩陣Ai。其具體操作過程如圖3所示。由于神經網絡在非線性自回歸模型中往往采用參數共享，因此難以通過網絡參數來判定某個序列xi是另一個序列xj的格蘭杰因果的充分條件，且這種方式也導致得到格蘭杰因果關系矩陣缺乏可解釋性［20］。因此，本文提出的MCGNN模型借鑒了文獻［20］的組件架構思想。在因果關系推斷中，對于每一個變量的時間序列數據，分別采用一個組件模型對其進行建模。將全部的多變量時間序列送入每一個組件中，并以預測其中一個時間序列的未來演變作為目標。這樣，多組件模型架構就增強了整個模型的可解釋性。

每個組件模型包含GCN和GRU兩部分。首先利用GCN來聚合含有格蘭杰因果關系的節點，表征多元序列之間的可能關系。在第i個組件中的GCN聚合過程如下式所示，GCN的原始輸入為多元時間序列X={x1，x2，…，xN}和隨機初始化的自適應參數矩陣Ai∈N×N，經過一次GCN卷積得到序列的表示Zi，該表示中包含了多元時間序列間的關系信息，公式為：

Zi=ReLU（AiXWi）。

式中：Wi為可學習的權重參數，Ai是模型訓練過程中需要學習的時間序列間的因果關系矩陣，在模型訓練過程中，通過最小化預測誤差來不斷更新Ai，從而迫使Ai不斷逼近真實的格蘭杰因果關系。

將當前t時刻GCN得到的表示Zti送入到GRU中，如下式所示。然后采用GRU學習單個時間序列的時變特征，捕獲各個序列上的時間依賴關系。其具體的計算過程如下公式所示：

Hti=GRUi（Ht－1i，Zti）。

在GRU中，接收兩個輸入，分別是上一時刻隱藏狀態Ut－1i和當前t時刻輸入Zti，在第i個組件中的GRU詳細計算過程如下。

uti=σ（WiuZti+UiuHt－1i+biu），

rti=σ（WirZti+UirHt－1i+bir），

ti=tanh（WihZti+Uih（rhi⊙Ht－1i）+bih），

Hti=uti⊙ti+（1－uti）⊙Ht－1i，

式中：uti表示更新門，biu表示更新門的偏置，rti表示重置門，bir表示重置門的偏置，ti表示候選隱藏狀態，bih表示隱藏狀態的偏置，σ表示Sigmoid激活函數，Hti為GRU輸出的時間序列的表示，該表示不僅包含了單個時間序列的時序信息，還包含了各時序變量間的關系信息。最后，模型經過一個全連接層得到預測輸出，如下式所示。

y＾i=WHti+bi，

式中：bi表示預測輸出的偏置。因果關系推斷模型的損失函數由兩部分構成，第一部分是采用均方誤差（MSE）計算時間序列的預測值與真實值的誤差，第二部分采用了L2正則項來保證格蘭杰因果關系的稀疏性，其公式如下所示。

loss=1M∑Ni=1∑Mj=1（yij－y＾ij）2+λ∑Ni=1‖Ai‖2，

式中：M表示樣本數量，N表示序列個數，yij表示第i個序列第j個樣本的真實值，y＾ij表示第i個序列的第j個樣本的預測值，λ表示懲罰系數，在實驗中取值為0.01。

1.4? 因果關系抽取

在因果關系推斷模型的訓練過程中，雖然能夠通過最小化模型的損失函數找到每一個組件中最優的格蘭杰因果矩陣Ai，但是這會造成每個組件中的格蘭杰因果矩陣Ai不一致，仍然無法對序列間關系進行確切的因果定義。為明確序列之間的因果關系，需要對學習到的格蘭杰因果矩陣Ai做出二元決策，判斷出兩個時間序列是否存在因果關系。這里采用圖4所示的因果關系抽取模塊提取出具體的因果關系矩陣A。

首先對每個組件中的因果矩陣Ai先取絕對值，再按列求均值，得到其余時間序列對于預測目標序列的平均貢獻度ai。

ai=1N∑NM=1AMi′，

在得到平均貢獻度ai后，采用一種異常值判斷方式對ai進行二元決策。二元決策的具體公式如下所示：

Mi=MEAN（ai），Si=STD（ai）? ，

ai=1，aiMi+γSi0，ai

計算每個向量ai的平均值Mi和標準差Si，然后根據每個序列的平均貢獻度與Mi+γSi（實驗中γ取值為2）的比值進行判斷，若貢獻度大于等于Mi+γSi，則表示存在因果關系，并設為1；若小于Mi+γSi，則不存在因果關系，值設為0。最后將二元決策后的結果進行拼接，A=1‖2‖…‖N，得到最終的因果圖A。

2? 試? 驗

為驗證MCGNN模型的有效性，分別在模擬數據集和真實數據集上進行了相關試驗。

2.1? 數據集

本文沿用文獻［20］的做法，分別采用模擬數據集Lorenz-96和真實數據集DREAM3評估MCGNN模型的有效性。現對兩種數據集分別進行介紹。

2.1.1? Lorenz-96模擬數據

Lorenz-96是1996年Lorenz和Saltzman提出的一種時間連續、空間離散的非線性氣候動力學模型［23］，其第i個變量的表達式為

dxtidt=（xt（i+1）－xt（i－2））xt（i－1）－xti+F ，

式中：F是一個強迫常數，它決定了時間序列數據中非線性和混沌的程度，F越大，數據變得越混沌。根據文獻［20］所述的模擬數據生成方法，在本實驗中設置F=10和F=40，并以Δt=0.05的采樣率對N=20的Lorenz-96模型進行數值模擬，生成具有稀疏格蘭杰因果關系的多元非線性時間序列。

2.1.2? DREAM3數據集

DREAM3數據集來源于一個基因調控網絡推理挑戰，該挑戰旨在從隨時間變化的基因表達數據集中估計格蘭杰因果網絡。DREAM3數據集是一個困難的、復雜的非線性數據集，其中包含5個不同的子數據集，分別是2個大腸桿菌（E.coli-1、E.coli-2）數據集和3個酵母（Yeast-1、Yeast-2、Yeast-3）數據集，每個數據集都表現出了不同的稀疏模式和因果拓撲結構。在每個數據集中包含了N=100個不同的時間序列，每個序列有46個擾動，每個擾動持續21個時間點，總共有966個時間點。

2.2? 試驗設置

本文所有試驗均采用Python編程語言和Pytorch深度學習框架，且在具有16 GB RAM的單個NVIDIA Tesla T4 GPU上進行運算。在訓練過程中，學習率設置為0.01，epoch設置為2 000。為了防止模型過擬合，采用Adam優化器［24］“早停法”（Early Stopping）進行訓練。同時，采用時間序列間的因果關系準確率（Accuracy）和接受者操作特征曲線下的面積（AUROC）這兩種評價指標對模型的推理結果進行評估，驗證模型有效性。

2.3? 基線模型

本文選取5種流行的生成序列間的格蘭杰因果關系的方法與本文所提出的MCGNN模型進行比較。（1）IMV_LSTM［25］：使用注意力權重來提供比標準LSTM更好的可解釋性，通過聚合注意力權重來檢測格蘭杰因果關系。（2）TCDF［26］：時間因果發現框架使用基于注意力的卷積神經網絡和因果驗證步驟相結合，通過解釋卷積網絡的內部參數來發現序列間的因果關系。（3）cLSTM［20］：利用LSTM和對權重的稀疏性懲罰，激勵特定的權重集為零的方式來生成序列間的格蘭杰因果關系。（4）cMLP［20］：利用多層感知機（Multipe Layer Perceptron，MLP）與lasso正則對權重參數進行稀疏性誘導，從而生成蘭杰因果關系。（5）SRU［27］：統計循環單元采用組件級預測模型對觀測數據的非線性進行建模，格蘭杰因果關系的網絡拓撲可以從SRU網絡的內部參數結構化稀疏估計中推斷出來。

2.4? 模型的性能表現

2.4.1? 模擬數據試驗

為驗證所提出的MCGNN模型對模擬數據的有效性，在時間序列長度為500（即T=500）且不同混沌程度（即F=10，F=40）的Lorenz-96數據集上進行了對比試驗，其中F值越大，表示該系統動力學變得越混亂。該試驗均選擇前5個時間步的序列數據作為輸入，預測下一時間步的序列數據。同時，本試驗以5次試驗的平均值作為試驗結果，并展示了其標準差，具體的實驗結果如表1所示。MCGNN模型相比于其他的基線模型在不同混沌程度的Lorenz-96模擬數據集上均表現出了最優的試驗結果。特別是當F=40時，大部分基線模型的格蘭杰因果檢測性能都顯著降低，如TCDF、cLSTM模型等。SRU模型在F=40時卻相較F=10時得到了較大提升，其原因為當時間序列的混沌程度較低、序列間的相互作用較弱時，該模型的正則化方法沒有充分發揮作用［25］。而MCGNN模型無論數據處于何種混沌程度，都保持著較強的競爭性，且格蘭杰因果關系檢測性能也相對平穩。

2.4.2? 真實數據集試驗

為驗證MCGNN模型在真實的復雜數據集中的格蘭杰因果推斷性能，采用因果關系推斷模型評價常用的基準數據（DREAM3基因表達數據）進行相關試驗。在試驗中，采用前5個時間步的序列數據作為輸入，預測下一時間步的序列數據，

在cLSTM和cMLP模型中分別設置隱藏單元為10個和5個，在MCGNN模型中設置隱藏單元為16個。采用AUROC作為性能指標比較各模型的因果推斷表現，結果如圖5所示：MCGNN模型在5個子數據集中均取得了不錯的表現，對于5個基因調控網絡中的E.coli-1、Yeast-1、Yeast-3數據集，MCGNN模型取得了最佳的AUROC，在Yeast-2上也表現優秀。

2.4.3? 樣本數量的影響

為驗證不同樣本數量對模型因果檢測性能的影響，分別在不同的時間序列長度（即T分別為250，500，1 000）的Lorenz-96數據集上進行了對比試驗，試驗結果如圖6所示。當F=10時，MCGNN模型在各個樣本數目中都取得了最佳的AUROC，且樣本數量越多，格蘭杰因果檢測的效果越好。并且，當可用的數據序列長度較少時（T=250），MCGNN模型性能表現明顯優于所有基線模型。當F=40時，即使時間序列的混沌程度增加，且在少樣本情況下，MCGNN模型的性能提升幅度明顯要優于大部分基線模型。

2.4.4? 模型參數量比較

為檢驗所提出的MCGNN模型的復雜度，在真實數據集DREAM3的子數據集E.coli-1上比較了不同方法在進行計算時所使用的參數量，其試驗結果如表2所示。TCDF模型在計算時參數量最少，但從模擬數據和真實數據的試驗結果來看，其效果表現得并不是很好。IMV_LSTM模型參數量最多，模型復雜，從表1和圖5的試驗結果來看，IMV_LSTM的性能表現也是最差的。本文所提出的MCGNN模型的參數量第二多，這主要是因為本模型采用了組件式結構，且每個組件模型包含了GCN和GRU，結構相對復雜。雖然cMLP和cLSTM模型也采用了組件式結構，結構相對簡單，但是綜合的表現性能卻不如MCGNN。總的來看，本文所提出的MCGNN模型去解決因果推斷任務相對于基線模型是有效且可行的。

2.5? MCGNN的工業應用

工業生產中往往涉及多維（即多變量）數據的監控和關系發現。如在天然氣生產工藝實時監測中，脫甲烷塔工藝過程所涉及的塔底、塔中及塔頂溫度和壓力等多維度參數，是影響產品回收率以及純度的關鍵因素。掌握脫甲烷塔工藝中各傳感位點之間溫度相互影響的規律是控制產品生產效能的有效途徑。在本實驗中，選取了脫甲烷塔中13個不同位置溫度傳感器點位的一個月數據記錄，共計732個時間點，部分點位溫度序列如圖7（a）所示。通過MCGNN模型挖掘這些點位之間的非線性依賴關系，從而為調控各個位置的溫度作出建議。

經MCGNN模型推斷，脫甲烷塔中溫度傳感器的因果網絡結構如圖7（b）所示，已知TT_016和TT_017點位處于脫甲烷塔的輸入部分，該位置的溫度是導致后續點位溫度變化的重要原因；TT_013、TT_014處于脫甲烷塔中部，該位置溫度容易受到塔頂和塔底溫度的影響；TT_021和TT_022處于脫甲烷塔的輸出部分，與塔內多個位置的溫度存在非線性依賴關系。這意味著，調節輸入位置以及塔頂、塔底點位的溫度，對于提升脫甲烷塔工藝效果相對重要。該結論經與采氣廠內部工藝專家校驗，證明多組件圖神經網絡方法較傳統基于LSTM的方法能更準確地識別出關鍵位點TT_021與TT_022，對于生產實踐具有一定指導意義。

3? 結? 論

本文提出的MCGNN模型首次將GCN和GRU網絡相結合應用到格蘭杰因果推斷任務中，同時考慮表征多元變量之間的可能關系和學習單個變量的時變特征。此外，為避免神經網絡的“黑盒”特性，MCGNN采用組件級模型架構，提高整個模型的可解釋性。該模型通過因果關系推斷和關系抽取2個過程實現多元序列間的因果關系推斷，即首先通過圖卷積和GRU網絡自動學習針對每個目標變量的因果結構，然后通過異常值檢測方法對生成的因果關系進行二元決策，從而得到序列間的格蘭杰因果關系。在模擬數據集和真實的基因調控網絡數據集上，該方法都獲得了最高準確率。將該方法應用于實際的天然氣生產工藝流程分析中，對脫甲烷塔中的溫度傳感器點位進行相關試驗分析，試驗結果與經驗知識吻合。然而，本方法的一個缺點在于計算復雜度較高。因此，在未來的工作中，將重點探索更高效的解決方案，減少模型復雜度。

參考文獻：

［1］? SHEIKHATTAR A，MIRAN S，LIU J，et al.Extracting neuronal functional network dynamics via adaptive Granger causality analysis［J］.Proceedings of the National Academy of Sciences，2018，115（17）：3869-3878.

［2］? WEIN S，MALLONI W M，TOM A M，et al.A graph neural network framework for causal inference in brain networks［J］.Scientific Reports，2021，11（1）：1-18.

［3］? XIU Y，REN X，ZHANG T，et al.Time labeled visibility graph for privacy-preserved physiological time series classification［C］//2022 7th International Conference on Cloud Computing and Big Data Analytics （ICCCBDA）.IEEE，Chengdu，China，2022：280-284.

［4］? ZHANG S，BAI Y，WU G，et al.The forecasting model for time series of transformer DGA data based on WNN-GNN-SVM combined algorithm［C］//2017 1st International Conference on Electrical Materials and Power Equipment （ICEMPE）.IEEE，Xian，China，2017：292-295.

［5］? ZHANG W，ZHANG C，TSUNG F.GRELEN：multivariate time series anomaly detection from the perspective of graph relational learning［C］//Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence，IJCAI-22.Messe Wien，Vienna，Austria.2022：2390-2397.

［6］? ZHOU L W，ZENG Q K，LI B.Hybrid anomaly detection via multihead dynamic graph attention networks for multivariate time series［J］.IEEE Access 2022，10：40967-40978.

［7］? VICENTE R，WIBRAL M，LINDNER M，et al.Transfer entropy—a model-free measure of effective connectivity for the neurosciences［J］.Journal of Computational Neuroscience，2011，30（1）：45-67.

［8］? AMBLARD P O，MICHEL O J J.On directed information theory and Granger causality graphs［J］.Journal of Computational Neuroscience，2011，30（1）：7-16.

［9］? SONG L，KOLAR M，XING E.Time-varying dynamic bayesian networks［J］.Advances in Neural Information Processing Systems，2009，22：1732-1740.

［10］KOLAR M，SONG L，AHMED A，et al.Estimating time-varying networks［J］.The Annals of Applied Statistics，2010：94-123.

［11］WANG Y，LIN K，QI Y，et al.Estimating brain connectivity with varying-length time lags using a recurrent neural network［J］.IEEE Transactions on Biomedical Engineering，2018，65（9）：1953-1963.

［12］KYONO T，ZHANG Y，VAN DER SCHAAR M.CASTLE：regularization via auxiliary causal graph discovery［J］.Advances in Neural Information Processing Systems，2020，33 ：1501-1512.

［13］HU W，YANG Y，CHENG Z，et al.Time-series event prediction with evolutionary state graph［C］//Proceedings of the 14th ACM International Conference on Web Search and Data Mining.Jerusalem，Israel，2021：580-588.

［14］XU C，HUANG H，YOO S.Scalable causal graph learning through a deep neural network ［C］// Proc of the 28th ACM international conference on information and knowledge management.New York：ACM Press，2019：1853-1862.

［15］MARCINKEVIS R，VOGT J E.Interpretable models for granger causality using self-explaining neural networks ［C］// Proc of the 9th International Conference on Learning Representations.2021.

［16］HUANG B，ZHANG K，ZHANG J，et al.Causal discovery from heterogeneous/nonstationary data［J］.The Journal of Machine Learning Research，2020，21（1）：3482-3534.

［17］KIPF T，WELLING M.Semi-supervised classification with graph convolutional networks［C］// International Conference on Learning Representation，San Juan，Puerto Rico，ICLR：1609.02907，2016.

［18］HUANG Y，KLEINBERG S.Fast and accurate causal inference from time series data［C］//FLAIRS Conference.The Diplomat Beach Resort Hollywood Curio Collection By Hilton，Hollywood，USA，2015：49-54.

［19］CHO K，VAN MERRIENBOER B，GULCEHRE C，et al.Learning phrase representations using RNN encoder-decoder for statistical machine translation ［C］// Proc of EMNLP.Stroudsburg，PA：ACL，Eighth Street，Stroudsburg PA 18360，2014：1724-1734.

［20］TANK A，COVERT I，FOTI N，et al.Neural granger causality［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，2021，44（8）：4267-4279.

［21］LI C，MO L，YAN R.Rolling bearing fault diagnosis based on horizontal visibility graph and graph neural networks［C］//2020 international conference on sensing，measurement & data analytics in the era of artificial intelligence （icsmd）.IEEE，2020：275-279.

［22］LORENZ E N，EMANUEL K A.Optimal sites for supplementary weather observations：Simulation with a small model［J］.Journal of the Atmospheric Sciences，1998，55（3）：399-414.

［23］KINGMA D P，BA J.Adam：a method for stochastic optimization ［C］// International Conference on Learning Representation，San Diego，CA，USA.ICLR：2015.

［24］GUO T，LIN T，ANTULOV-FANTULIN N.Exploring interpretable lstm neural networks over multi-variable data ［C］// International conference on machine learning.Long Beach，California，USAPMLR，2019：2494-2504.

［25］PLETNEV A，RIVERA-CASTRO R，BURNAEV E.Graph Neural Networks for Model Recommendation using Time Series Data［C］//2020 19th IEEE International Conference on Machine Learning and Applications （ICMLA）.IEEE，2020：1534-1541.

［26］KHANNA S，TAN V Y F.Economy statistical recurrent units for inferring nonlinear granger causality［C］// International Conference on Learning Representation，Addis Ababa 2020.

［27］CUI Y，ZHENG K，CUI D，et al.METRO：a generic graph neural network framework for multivariate time series forecasting［J］.Proceedings of the VLDB Endowment，2021，15（2）：224-236.

Causality Inference for Multivariate SeriesBased on Multi-component Graph Neural Network

ZHANG You-xing1，LI Ping2，WU Rong1，YANG Xiao-li1，LI Yu-dong1，MENG Liang1

（1.Information Management Station，No.1 Gas Production Plant of Xinjiang Oilfield Company，Karamay Xinjiang 834000，China;2.College of Computer Science，Southwest Petroleum University，Chengdu Sichuan 610500，China）

Abstract：Considering that graph neural networks are capable of capturing nonlinear and high-order interactions，this paper proposes a Granger causality inference method （MCGNN） for multivariate time series based on multi-component graph neural network to improve the interpretability and accuracy of Granger causal inference.Multi-component graph convolution neural network is utilized to obtain the nonlinear effects between multivariate time series and Gated Recurrent Unit model is introduced to model the time series，translating the causality inference into time series predictions.The experimental results indicate that MCGNN is significantly better in accuracy than the current best models in both open simulated data and real data sets.In particular，when it is applied to the data set of natural gas cryogenic process，the method can dynamically find the causal relationship between the site sensors in cryogenic process，which is consistent with the judgment of cryogenic process experts.

Keywords：Granger causality；graph neural network；multi-variable time series; nonlinear effects; high-order interaction