基于參數估計-滑模阻抗控制的SEA性能分析

曹學鵬 張正 李彩紅 魯航

doi： 10.11835/j.issn.1000-582X.2023.226

收稿日期：2023-03-15

網絡出版日期：2023-12-12

基金項目：國家自然科學基金資助項目（51509006）；先進節能教育部工程中心開放課題（SWEDT-KF201902）。

Foundation：Supported by National Natural Science Foundation of China（51509006） and Engineering Research Center of Advanced Drive Energy Saving Technologies， Ministry of Education（SWEDT-KF201902）.

作者簡介：曹學鵬（1982—），男，教授，主要從事流體動力與控制、機電液一體化系統及裝備研究，（E-mail） tiepeng2001@chd.edu.cn。

摘要：重載四足機器人的足部與地面接觸過程和步態轉換過程中會受到不確定的沖擊載荷作用，易導致足部機構載荷過大從而造成結構的沖擊損壞。因此，針對使用液壓串聯彈性執行器（series elastic actuators，SEA）作為足部末端在非結構環境下動態性能差的問題，提出了基于環境參數估計的滑模阻抗控制方法（environmental parameter estimation sliding mode，EPESM）。以閥控液壓缸的活塞位移傳遞函數為基礎建立了基于位置內環的SEA阻抗控制模型，并以PID作為基礎控制器；為改善SEA阻抗控制的動態性能，根據Lyapunov第二法構建穩定的自適應環境參數估計方法對SEA期望位置進行前饋補償；為提升自適應環境參數估計方法在SEA工作過程中不同階段的動態性能和環境變化適應性，使用模糊控制方法對自適應環境參數估計方法中的自適應參數進行尋優；以SEA狀態方程為基礎構建滑模控制器與PID控制器進行動態性能對比分析。仿真結果表明：在變SEA彈簧剛度工況和變環境剛度下，EPESM阻抗控制的響應速度明顯更快，可將調節時間從平均5 s縮短到1 s內，能更快地達到預期位移和預期接觸力，且能略微降低穩態誤差，使接觸力誤差保持在±6 N內。在動態跟蹤工況下，EPESM阻抗控制的動態性能更好，在快速進入跟蹤狀態后，可以長時間保持0.2 s以內的相位滯后和5.2%的幅值誤差。

關鍵詞：重載機器人；串聯彈性執行器；阻抗控制；模糊-自適應參數估計；滑模控制

中圖分類號：TP242? ? ? ? ? 文獻標志碼：A? ? ? ? 文章編號：1000-582X（2024）05-001-12

SEA performance analysis based on parameter estimation-sliding mode impedance control

CAO Xuepeng， ZHANG Zheng， LI Caihong， LU Hang

（Mechatronics Institute of Mechanical Engineering School， Changan University， Xian 710064， P. R. China）

Abstract： Heavy quadruped robots are subjected to uncertain impact loads during foot-to-ground contact and gait transition， which can easily lead to excessive load on the foot mechanism and structural impact damage. Therefore， a sliding mode impedance control method based on environmental parameter estimation （EPESM） was proposed to solve the problem of poor dynamic performance when using hydraulic series elastic actuators （SEA） as foot ends in unstructured environments. Based on the piston displacement transfer function of the valve controlled hydraulic cylinder， an SEA impedance control model based on the position inner loop is established， with PID serving as the basic controller. To improve the dynamic performance of SEA impedance control， a stable adaptive environment parameter estimation method based on Lyapunovs second method is constructed to compensate for the expected SEA position using feed forward compensation. To improve the dynamic performance and adaptability of adaptive environmental parameter estimation methods at different stages of SEA work， fuzzy control methods are used to optimize the adaptive parameters in these methods. Based on the SEA state equation， a sliding mode controller and a PID controller are constructed for dynamic performance comparison and analysis. Simulation results show that under variable SEA spring stiffness and variable ambient stiffness conditions， the response speed of EPESM impedance control is significantly faster. The adjustment time can be significantly reduced from an average of 5 s to within 1 s， achieving faster expected displacement and expected contact force， while keeping the steady-state error slightly reduced and the contact force error within ±6 N. Under dynamic tracking conditions， EPESM impedance control exhibits better dynamic performance， maintaining a phase delay within 0.2 s and an amplitude error of 5.2 % for an extended period after quickly entering the tracking state.

Keywords： heavy load robot; series elastic actuator; impedance control; fuzzy-adaptive parameter estimation; sliding mode control

隨著工業現代化的深入發展，足式機器人發展迅速且應用廣泛[1]。足式機器人足部與地面接觸和步態轉換過程中會受到沖擊載荷的作用，易導致足部機構載荷過大，造成足部機構的損壞。對重載足式機器人而言，這種不確定的沖擊造成的影響更嚴重。因此，需要對行走過程中的足部進行柔順控制。使用液壓串聯彈性執行器[2]（series elastic actuators，SEA）作為重載足式機器人的腿部結構時，可通過其串聯的彈性元件實現對輸出力或位置的柔順控制[3-4]。

柔順控制的研究多集中于主動柔順控制，如羅建雄等[5]采用變阻尼的阻抗控制實現了針對液壓機械臂的主動柔順控制。也有研究使用直接力控方法進行阻抗控制[6-8]。Li等[9]使用了改進自適應布谷鳥優化BP神經網絡算法建立力預測控制模型進行直接力控。沈雙等[10]利用BP神經網絡整定PID參數獲得更好的控制性能。Asignacion等[11]將降噪擾動觀測器應用于SEA的內環速度控制，提升了整體的控制性能。在傳統阻抗控制中，機器人的阻抗特性一般是事先預設且在機器人運行過程中不變的。單一的阻抗特性難以滿足變化環境下的動態性能。目前主要的解決方式是讓機器人自動調整阻抗特性參數以適應變化的環境[12]。Huang等[13]采用一種基于廣義模糊神經網絡的自適應阻抗控制實現了對未知環境模型的良好適應性。Yu等[14]使用貝葉斯方法估計外界人體阻抗和運動意圖以提升系統性能。Chatterjee等[15]提出一種基于雙擴展卡爾曼濾波器的被動阻尼串聯彈性傳輸阻抗在線估計方法，通過實時估計阻抗提升了控制器的可靠性。針對未知的外界環境，Han等[16]在康復機器人中應用迭代學習算法進行阻抗自適應控制。

在目前輕功率SEA主動柔順控制方法的基礎上，筆者以重載機器人的SEA腿部執行機構為研究對象，分析其在不同接觸環境和SEA變彈簧剛度下的動態性能。采用結合模糊優化的自適應參數估計方法對期望位移進行補償，結合滑模控制器替代傳統的PID控制器，利用其對模型參數變動不敏感的特性提升SEA對環境變化和模型變化的適應性，保證了SEA響應過程的快速和準確性。

1 SEA阻抗控制模型

1.1 液壓SEA建模

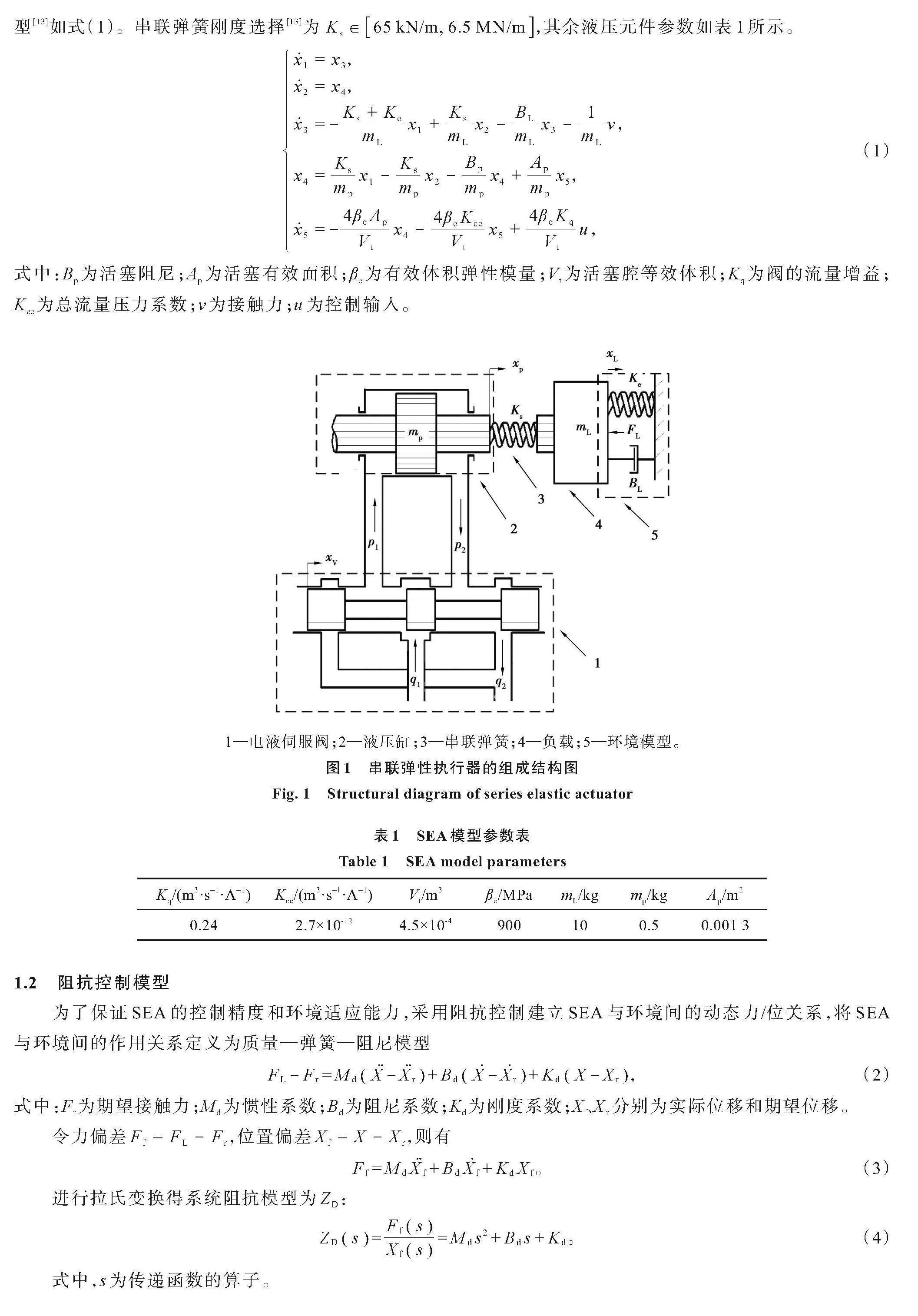
參照團隊已有的研究成果[17]，不考慮多個執行器之間的運動耦合，對圖1的串聯執行器進行液壓SEA的建模。圖中，、分別為閥進油流量和閥回油流量；為閥芯位移；、分別為閥進油壓力和閥回油壓力；FL為實際接觸力；Ke為環境剛度；mL為負載質量；BL為環境阻尼；mp為活塞質量。由于使用的模型參數一致，不再對建模過程和參數計算過程進行贅述。對液壓串聯SEA系統進行建模[18]，取狀態變量，xL為負載位移，xp為活塞位移，pL為負載壓力。可得SEA模型[13]如式（1）。串聯彈簧剛度選擇[13]為 ，其余液壓元件參數如表1所示。

（1）

式中：Bp為活塞阻尼；Ap為活塞有效面積；βe為有效體積彈性模量；Vt為活塞腔等效體積；Kq為閥的流量增益；Kce為總流量壓力系數；為接觸力；為控制輸入。

1—電液伺服閥；2—液壓缸；3—串聯彈簧；4—負載；5—環境模型。

1.2 阻抗控制模型

為了保證SEA的控制精度和環境適應能力，采用阻抗控制建立SEA與環境間的動態力/位關系，將SEA與環境間的作用關系定義為質量—彈簧—阻尼模型

， （2）

式中：Fr為期望接觸力；Md為慣性系數；Bd為阻尼系數；Kd為剛度系數；、分別為實際位移和期望位移。

令力偏差，位置偏差，則有

。 （3）

進行拉氏變換得系統阻抗模型為：

。 （4）

式中，為傳遞函數的算子。

采用阻抗控制原理對重載SEA柔性閥控缸的負載端建模，定義串聯彈簧的壓縮量，為活塞位移；為末端位移。阻抗控制模型可表示為

。 （5）

式（5）可化為

。 （6）

由式（5）和式（6）可得重載SEA的負載位移為

， （7）

式中：mL取10 kg，Bp取100 N·s/m。

結合柔性閥控缸模型，SEA基于PID位置內環的阻抗控制[19]原理如圖2所示。

2 SEA自適應環境參數估計滑模阻抗控制

2.1 模糊-自適應環境參數估計

基于自適應環境參數估計的滑模控制器（environmental parameter estimation sliding mode，EPESM）通過實時計算SEA與環境間的接觸力誤差，實時調節自適應環境參數估計的參數，修正預期參考位置，從而控制SEA末端位置以及與環境的接觸力。若能實時估計環境位置和剛度信息，可得到SEA所接觸環境的線性模型，實現SEA的力/位跟蹤控制。

當時，即SEA與環境間接觸力誤差為0時，根據可將表示為，其中、、、分別是環境位置和剛度的實際值與估計值。

定義變量為

， （8）

則SEA與環境間接觸力的估計值與實際值之差可表示為

。 （9）

根據式（9），可得，是2×2非奇異正定實對稱矩陣。通過實時調節環境參數估計值、，可使，則。根據Lyapunov第二法構建二次型標量函數

。 （10）

對二次型標量函數求導，由結果可得參數估計是穩定的：

。 （11）

對直接求解，得

（12）

式中，、是自適應參數，為正常數。

對式（12）積分得環境參數估計值的表達式：

（13）

式中：為時間；為初始時刻。

基于環境參數估計的SEA自適應阻抗控制使用環境位置及剛度信息的估計值代替模型數值，以此對SEA期望位移進行前饋補償。為進一步提高環境參數估計的性能，使用模糊控制器以重載SEA系統偏差和偏差的變化量作為輸入，建立與自適應控制參數、間的模糊關系。因自適應控制參數、之間存在比例關系，可以改為控制自適應參數和比例系數。重載SEA的模糊-自適應阻抗控制系統如圖3所示，其中e為力的誤差。

模糊輸入量為力的偏差，通過力的偏差估計環境剛度并對期望位移進行補償。當正偏差較大且變化率為正、或負偏差較大且變化率為負時，應減小估計值的影響，增大，減小。當正偏差較大且變化率為負、或負偏差較大且變化率為正時，應增大估計值的影響，減小，增大。其余情況的規則設置類似。輸入量模糊變量的變化范圍取自力誤差的典型變化曲線極值分別為：=[-2 000， 2 000]，=[-4 000， 4 000]。自適應參數取值范圍過小會導致響應變慢，取值范圍過大會導致超調上升，綜合考慮響應速度和超調影響，最終選擇輸出參數范圍為=[0， 0.005]，=[0， 10]，模糊語言的子集用對應的NB、NM、NS、ZO、PS、PM、PB表示。模糊控制規則如表2所示。隸屬函數為梯形分布，其中對應于PB和NB的半梯形分布各占輸入范圍的20%，保證在偏差較大時能夠獲得更大的響應速度，其余區間采用均布。采用面積重心法進行反模糊，使參數估計模塊的輸出盡量平滑，避免對滑模控制器產生干擾。

2.2 滑模控制器設計

針對重載SEA工作在非結構環境中的抗干擾能力需求，使用滑模控制作為控制策略[20?21]。滑模控制具備良好的魯棒性，對于參數變化及外部干擾有極佳的不敏感性。以團隊前期工作已確定的閥控缸狀態方程為基礎[17]，以位置偏差及其導數作為滑模控制器的輸入，以控制器輸出調整電液伺服閥的開口大小，系統的誤差變量可定義為：

（14）

定義滑模面，求導得：

。 （15）

選擇趨近律為飽和函數，為增益系數，在邊界層內呈線性變化。由于控制對象閥控缸SEA設定的最高運動速度為0.054 m/s，速度較低，飽和函數趨近律可在一定程度上抑制抖振。此外，邊界層厚度也影響抖振大小，因此設置一個較大的初始邊界層厚度，使z與滑模面距離小于時，自動切換到更小的邊界層，以此削弱抖振并保證響應速度。可變邊界層厚度可描述為，均為正常數。當距離大于E時，；當距離小于等于E時，。聯立趨近律和式（15）得控制器輸出為。

， （16）

。 （17）

根據滑模可達性條件，對趨近律進行穩定性分析如下，可得系統是穩定的。

。 （18）

式中，

（19）

在SIMULINK中搭建重載SEA的EPESM阻抗控制模型，如圖4所示。圖中，滑模阻抗控制模塊為基于位置阻抗控制的重載SEA力位控制系統模型，控制器使用上述的滑模控制器。自適應環境參數估計使用和作為參數實現對期望位置的前饋補償，自適應參數的調整由模糊尋優模塊自動調整。

圖4 EPESM的SIMULINK模型

Fig. 4 SIMULINK model for EPESM

3 系統性能分析

為了研究分析SEA的動態性能，在此設定一個參照工況，為后續變參數仿真提供基礎工況設定，參照工況示意圖如圖5所示，左側的SEA及mL負載代表腿部執行器，右側彈簧代表地面環境。地面初始位置為L1，當執行器與地面接觸并產生接觸壓力后，最終平衡位置為L2。參照工況的串聯彈簧剛度和環境參數均為定值，參數值如表3所示。環境剛度參數參考文獻[22]中測得的沙地、潮濕土地和硬質皮地面參數進行設置。預期參考位置L1為0.05 m，最終預期的力平衡位置L2=Xd，預期接觸力為2 000 N，兩者均為階躍輸入信號。阻抗控制參數設置為Md=10， Bd=2 000， Kd=9×104。通過對比固定自適應參數的PID控制方法（后續簡稱為PID控制）與模糊優化自適應參數的滑模控制方法（后續簡稱為EPESM）對系統進行性能分析。初始狀態下機器人足部與環境并未接觸，距離為0.05 m，性能分析起始時刻為接觸的瞬間時刻。

3.1 變彈簧剛度性能分析

在參照工況基礎上，通過改變串聯彈簧剛度分析SEA的動態性能。根據1.1節液壓SEA建模小節中串聯彈簧剛度的范圍，在串聯彈簧剛度Ks為65、90、650 kN/m這3種工況下，可獲得分別采用固定自適應參數的PID控制方法和EPESM阻抗控制的SEA末端位移及末端接觸力。

采用2種控制方法的SEA末端位移如圖6。PID控制的末端位移的穩態值分別為、、 cm；穩態位置誤差分別為0.57%、0.34%、0.12%；調節時間為4.9、4.3、3.4 s。EPESM阻抗控制的末端位移的穩態值分別為、、 cm；穩態位置誤差分別為0.07%、0.05%、0.01%；調節時間分別為0.7、0.6、0.4 s。模糊優化的自適應參數隨著誤差的減小而減小，可提升響應動態性能，減小超調量的大小。

SEA末端接觸力如圖7所示。PID阻抗控制的末端接觸力穩態值分別為2 050.2、2 027.3、1 991.6 N，穩態力誤差分別為2.50%、1.36%、0.41%；調節時間為3.95、3.90、3.14 s。EPESM阻抗控制的末端接觸力的穩態值分別為2 004.2、2 002.8、1 999.5 N，穩態力誤差分別為0.21%、0.14%、0.03%；調節時間為0.8、0.7、0.6 s。

仿真結果表明，隨著串聯彈簧剛度增大，SEA的控制性能略微提高。在不同彈簧剛度下，相比于PID阻抗控制方法，EPESM阻抗控制的響應速度更快，可將調整時間縮短到1 s內，且穩態誤差更小。因此，當SEA內部串聯彈簧變化時，EPESM阻抗控制方法能夠更好地適應重載SEA內部參數的變化。

3.2 變環境剛度性能分析

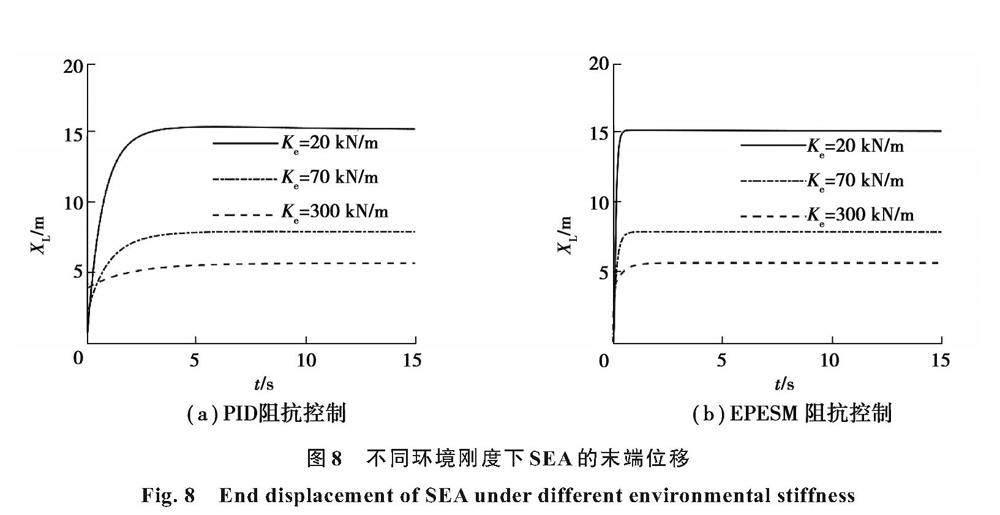
在參照工況的基礎上，通過改變環境剛度分析SEA的動態性能。參照劉帥等[22]的沙地、潮濕土地和硬質皮地面的地面剛度特征進行工況設置，沙地、潮濕土地和硬質皮地面的環境剛度Ke分別為20、70、350 kN/m。SEA在3種不同環境工況下的預期參考位置分別為15.00、7.86、5.67 cm。

采用2種阻抗控制的末端位移如圖8所示，PID阻抗控制的末端位移在3種環境工況下分別為、、 cm；末端位移穩態誤差分別為1.26%、0.63%、0.52%；調整時間分別為3.3、3.8、4.7 s。EPESM阻抗控制的末端位移在3種環境工況下分別為、、 cm；末端位移穩態誤差分別為0.13%、0.05%、0.04%；調整時間分別為0.5、0.6、0.9 s。

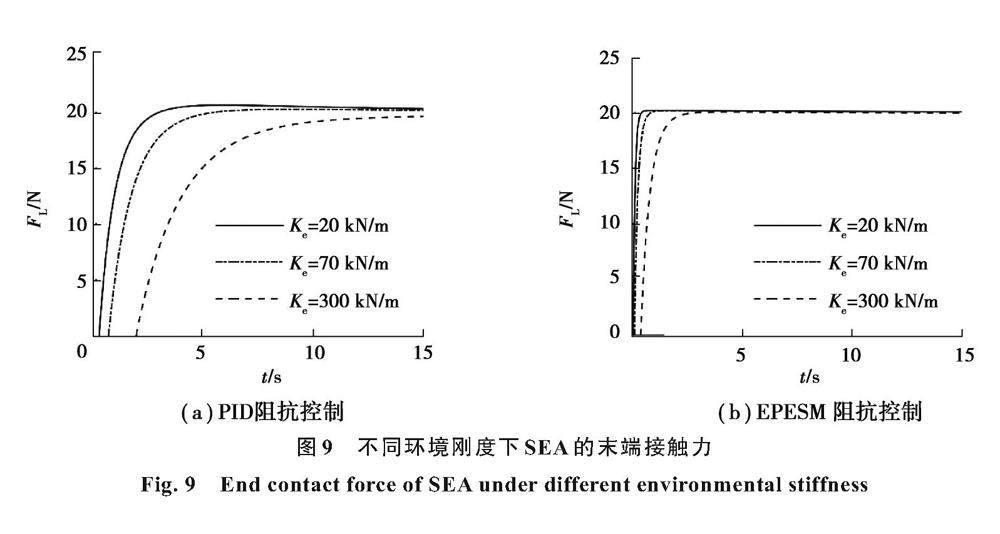
采用2種阻抗控制的末端接觸力如圖9所示，PID阻抗控制的末端接觸力在3種環境工況下分別為2 035.1、2 019.6、1 980.9 N；末端位移穩態誤差分別為1.75%、0.98%、0.95%；調整時間分別為3.1、6.1、15.0 s。EPESM阻抗控制的末端接觸力在3種環境工況下分別為2 004.2、2 002.8、1 994.8 N；末端位移穩態誤差分別為0.21%、0.14%、0.26%；調整時間分別為0.6、1.1、2.7 s。

仿真結果表明，隨著環境剛度增大，SEA穩態位置誤差略微減小。由于硬質地面的環境剛度較大，即使較小的穩態位置誤差也會造成較大穩態力誤差。在不同環境剛度的工況下，相比于PID阻抗控制， EPESM控制響應速度明顯更快，穩態誤差更小，對外部作業環境的變化具有良好的適應性。

3.3 動態跟蹤性能分析

以上2組仿真工況都是SEA在自由空間運動至接觸環境的恒力/位置控制。在實際工況中，要求SEA的負載位移和負載輸出力是變化的。因此，在參照工況基礎上，通過改變SEA與環境間的預期接觸力及位置分析SEA的動態性能，在此采用正弦波信號作為接觸力輸入，采用正弦波信號作為末端位移輸入。

采用2種阻抗控制的末端位移如圖10所示，傳統PID阻抗控制的末端位移范圍為[ cm，? cm]，滯后0.7 s，振幅誤差57.9%。EPESM阻抗控制的末端位移范圍為[ cm，? cm]，滯后0.19 s，振幅誤差5.2%。

采用2種阻抗控制的末端位移如圖11所示，傳統PID阻抗控制的末端接觸力范圍為[1 332.9 N， 1 754.1 N]，滯后0.7 s，振幅誤差57.9%。EPESM阻抗控制的末端接觸力范圍為[1 041.3 N， 1 989.1 N]，滯后0.19 s，振幅誤差5.2%。自適應參數的模糊輸出如圖12所示，輸出的波動來源于正弦信號波峰處的誤差變化。

仿真結果表明，在正弦波信號跟蹤工況下，相比于傳統PID阻抗控制，EPESM阻抗控制響應速度更快，滯后時間減少72.9%，振幅誤差小91%，具有更好的動態力/位置跟蹤性能。

4 結 論

1）為滿足對重載液壓SEA進行阻抗柔順控制，在閥控缸傳遞函數的基礎上，建立了基于位置內環的阻抗控制模型。為提升SEA的動態性能，使用環境參數估計方法對期望位置進行前饋補償。

2）為提升環境參數估計方法對不同環境的適應性，采用模糊控制方法對自適應參數進行調節，提升SEA的動態響應性能，并結合滑模控制提升阻抗控制的性能。

3）在非結構環境工況中，將EPESM阻抗控制與傳統PID阻抗控制進行性能對比分析。在變SEA彈簧剛度工況和變環境剛度下，EPESM阻抗控制的響應速度明顯更快，調節時間明顯縮短，能更快地達到預期位移和預期接觸力，且能略微降低穩態誤差。在動態跟蹤工況下，EPESM阻抗控制的動態性能更好，可以長時間保持較低的相位滯后和較高的跟蹤精度。

參考文獻

［1］? Biswal P， Mohanty P K. Development of quadruped walking robots： a review[J]. Ain Shams Engineering Journal， 2021， 12（2）： 2017-2031.

［2］? Shi Y， Wang P， Zha F， et al. Mechanical design and force control algorithm for a robot leg with hydraulic series-elastic actuators[J]. International Journal of Advanced Robotic Systems， 2020， 17（3）： 172988142092101.

［3］? Kong K， Bae J， Tomizuka M. A compact rotary series elastic actuator for human assistive systems[J]. IEEE-Asme Transactions on Mechatronics， 2012， 17（2）： 288-297.

［4］? Jiang J， Wang Y， Cao H， et al. A novel pump-valve coordinated controlled hydraulic system for the lower extremity exoskeleton[J]. Transactions of the Institute of Measurement and Control， 2020， 42（15）： 2872-2884.

［5］? 羅建雄， 趙慧， 蔣林. 基于液壓機械臂的主動柔順控制[J]. 武漢科技大學學報， 2022， 45（2）： 127-134.

Luo J X， Zhao H， Jiang L. Active compliance control based on hydraulic manipulator[J]. Journal of Wuhan University of Science and Technology， 2022， 45（2）： 127-134.（in Chinese）

［6］? Xu Z， Li S， Zhou X， et al. Dynamic neural networks for motion-force control of redundant manipulators： an optimization perspective[J]. IEEE Transactions on Industrial Electronics， 2021， 68（2）： 1525-1536.

［7］? Zhu R， Yang Q， Chen C， et al. Force-based active compliance control of hydraulic quadruped robot[J]. International Journal of Fluid Power， 2021， 22（2）： 147-172.

［8］? Shen W， Lu X B， Ma C J. Robust force tracking control via backstepping sliding mode control and virtual damping control for hydraulic quadruped robots[J]. Journal of Central South University， 2020， 27（9）： 2673-2686.

［9］? Li B， Zhang Y， Yuan L， et al. Predictive control of plantar force and motion stability of hydraulic quadruped robot[J]. China Mechanical Engineering， 2021， 32（5）： 523-532.

［10］? 沈雙， 雷靜桃， 張悅文. 仿生跳躍機器人氣動串聯彈性關節的位置/剛度控制[J]. 中國機械工程， 2021， 32（12）： 1486-1493.

Shen S， Lei J T， Zhang Y W. Position and stiffness control of pneumatic series elastic joints for bionic jumping robots[J]. China Mechanical Engineering， 2021， 32（12）： 1486-1493.（in Chinese）

［11］? Asignacion A， Haninger K， Oh S， et al. High-stiffness control of series elastic actuators using a noise reduction disturbance observer[J]. IEEE Transactions on Industrial Electronics， 2022， 69（8）： 8212-8219.

［12］? Chen Z， Wang S， Xu K， et al. Research on high precision control of joint position servo system for hydraulic quadruped robot[C]//2019 Chinese Control Conference （CCC）， Guangzhou， China. IEEE， 2019： 755-760.

［13］? Huang H， Yang C， Chen C L P. Optimal robot-environment interaction under broad fuzzy neural adaptive control[J]. IEEE Transactions on Cybernetics， 2021， 51（7）： 3824-3835.

［14］? Yu X， He W， Li Y， et al. Bayesian estimation of human impedance and motion intention for human-robot collaboration[J]. IEEE Transactions on Cybernetics， 2021， 51（4）： 1822-1834.

［15］? Chatterjee S， Sen S， Majumder S. Impedance estimation of a nonlinear flexible mechanical transmission using a dual ekf[J]. IFAC-PapersOnLine， 2022， 55（1）： 315-320.

［16］? Han S S， Wang H P， Yu H Y. Human-robot interaction evaluation-based aan control for upper limb rehabilitation robots driven by series elastic actuators[J].? IEEE Transactions on Robotics， 2023， 39（5）： 3437-3451.

［17］? 曹學鵬， 魯航， 朱文鋒， 等. 變負載下機器人液壓串聯彈性執行器動態位置控制方法[J]. 西安交通大學學報， 2022， 56（4）： 91-100.

Cao X P， Lu H， Zhu W F， et al. Dynamic position control method for hydraulic series elastic actutor of robot under variable load[J]. Journal of Xian Jiaotong University， 2022， 56（4）： 91-100.（in Chinese）

［18］? Sun H， Tao J， Qin C， et al. Dynamics modeling and bifurcation analysis for valve-controlled hydraulic cylinder system containing counterbalance valves[J]. Journal of Vibration Engineering & Technologies， 2021， 9（8）： 1941-1957.

［19］? Sun T， Peng L， Cheng L， et al. Stability-guaranteed variable impedance control of robots based on approximate dynamic inversion[J]. IEEE Transactions on Systems， Man， and Cybernetics： Systems， 2019， 51（7）： 4193-4200.

［20］? Takanori T， Takuma T， Yutaka T， et al. Hydro-disk-type of electrorheological brakes for small mobile robots[J]. International Journal of Hydromechatronics， 2021， 4（2）： 99-115.

［21］? Hu H， Wang X， Chen L. Impedance sliding mode control with adaptive fuzzy compensation for robot-environment interacting[J]. IEEE Access， 2020， 8： 19880-19889.

［22］? 劉帥， 趙慧， 劉清宇. 四足機器人軟硬地面穩定過渡的腿部主動變剛度調節策略[J]. 工程科學學報， 2022， 44（3）： 420-429.

Liu S， Zhao H， Yu L Q. Active and variable stiffness adjustment strategy for legs of quadruped robot for stable transition between soft and hard ground[J]. Chinese Journal of Engineering， 2022， 44（3）： 420-429.（in Chinese）

（編輯? 詹燕平）