指向核心素養的高中數學深度學習探究

毛世勤

【摘要】在核心素養導向下，深度學習的實施，可以讓學生更好地認識數學學科的本質，提高學生關鍵能力和思維品質.文章基于核心素養的視角，提出了包括更新教學理念、把準實際學情、創設問題情境、師生雙向互動、創設有效問題等高中數學深度學習的策略，旨在通過這些策略幫助學生更好地理解和應用數學知識，培養他們的數學思維和解決問題的能力，獲得適應終身發展的品質和素養，從而讓數學核心素養在深度學習課堂上落地生根.

【關鍵詞】高中數學；深度學習；數學核心素養；品質和素養

高中數學核心素養是高中數學課程評價的重要目標，是落實立德樹人根本任務的重要舉措，也是培養新時代創造性人才的重要方向.數學核心素養是在解決數學問題的實踐中，逐漸養成的數學品格和綜合性能力.培養學生數學核心素養在提升學生數學實踐能力，發展學生理性思維，豐富學生數學知識儲備等方面有著非常重要的現實意義.深度學習強調學習過程中形成的能力，其與核心素養中的“關鍵能力”“必備品格”有著密切的聯系.研究深度學習，并將其實踐到高中數學課堂教學中，不僅可以優化學生的知識結構，提高學生分析和解決問題的能力，而且可以提升適應學生終身發展的品質和素養.以下是筆者就深度學習的內涵，及深度學習的落實談的幾點自己的認識，若有不足，請指正.

一、深度學習的內涵

深度學習也稱為深層學習，其強調主動理解與批判接受，強調數學本質與數學思想方法，它是發展學生高階思維，提高學生分析和解決問題的重要途徑.深度學習是淺層學習的延續和深化，它是一種主動的、探索式的、理解式的學習方式.深度學習可以讓學生積極主動地、批判地學習新知識和新思想，有效提高學生主體思維的參與，讓學生在高階思維中主動進行知識的建構、轉化和遷移，以此讓學生獲得可持續學習的能力，促進學生數學核心素養的落實.

深度學習與深度教學密不可分，深度學習的發展離不開教師的精心設計和耐心指導.在數學教學中，教師應發揮好課堂領導者的作用，結合教學內容和學生學情精心設計和規劃，讓學生在其引導下積極地互動，以此通過不同思維的碰撞與情感的交流引發高階思維，促進學生深度學習的達成.

另外，深度學習強調學生的學習過程，其可有效彌補淺層學習中存在的碎片化、淺表化、浮躁化等缺陷，充分調動學生學習的主動性、積極性，實現教師、學生和教學內容的高度統一，實現教學相長.同時，深度學習為學生提供了自主探索的空間，可以促進學生的深度參與、深度思考和深度感悟，有效促進學生數學核心素養的培養.

二、實現深度學習的有效策略

在新課改背景下，高中數學課堂的教學方式、教學手段、學習方式等都發生了許多變化，但是教學中仍然存在著一些問題，如教學中忽視知識的前后聯系，使學生的知識結構呈現零散性和碎片化；教學中片面地追求速度，使學生對知識的理解局限于識記，缺乏對知識與技能背后數學思想方法的感悟；教學中忽視了學生的主體價值，影響學生參與課堂的積極性.為了改變這一局面，高中數學課堂學習必須走向“深度學習”.筆者結合教學實踐淺談幾點實現深度學習的有效策略，供參考！

（一）更新教學理念，激活學習動力

在數學學習的過程中，若過多地強調智力因素對數學成績的影響，而忽視非知識因素的影響，則很容易讓學生因為感覺數學難學而放棄學習數學.要知道，數學學習不僅需要智力因素的積極參與，也要非智力因素的積極配合，只有幫助學生樹立正確的學習態度，才能讓學生全身心地投入數學學習中，從而讓深度學習真正地發生.另外，只有讓學生深度投入，才能讓學生充分體驗學習的樂趣，從而激活學生學習動力，讓學生逐漸走上樂學、會學之路.

例如，在講解等比數列通項公式時，教師可以改變傳統的“講授+練習”的教學模式，以趣味性問題為線索，誘發學生深度思考，開展深度學習.問題如下：將一張厚度為0.1mm的報紙對折2次，這疊紙多厚？如果將報紙對折30次，這疊紙大概多厚呢？如果對折100次呢？教學中，教師提供時間讓學生思考、猜想、探索，鼓勵學生大膽說出自己的想法.在學生做出種種估計后，教師給出答案，學生發現自己的猜想與實際結果相差甚遠，由此讓學生產生強烈的探究欲，進而全身心地投入等比數列通項公式的學習中，這有效激發了學生學習的內驅力，促成深度學習.

（二）把準實際學情，確定發展目標

數學課堂教學的主體是學生，若想調動學生的主體性和積極性，教師的精心設計必不可少.可見，深度學習離不開深度教學，而深度教學離不開教師的精心設計和規劃.教師作為課堂教學的組織者，要立體式地分析學生的學習，把準學情，找準“最近發展區”，精準定位深度學習的學習目標，激發學生內驅力，促進深度學習的發生.教學中，教師要了解學生的“過去”，分析學生已有的知識儲備、認知經驗和思維水平，預估通過深度學習能夠掌握的知識，提升的能力與素養，以此制定促成高階思維的課程目標.

例如，在教學“對數函數”時，若教師直接將定義、圖像、性質等呈現給學生，讓學生理解和識記，則學生可能很難與指數函數建立聯系，這樣不僅會影響新知的學習效果，而且會影響學生認知體系的建構.基于此，在實際教學中，教師應先引導學生回顧指數函數的相關內容及學習過程，這樣既可以了解學生對指數函數及其圖像、性質的掌握情況，又能有效溝通二者的內在聯系，讓學生通過類比順利地理解和掌握對數函數的特性.在探索對數函數的性質時，教師可以借助圖像引導學生觀察、抽象，如教學中可以讓學生探索y=loga（x+b）（a>0且a≠1）與y=logax（a>0且a≠1）圖像之間的關系.這樣以學生的已有知識和已有經驗為線索，引導學生進行類比分析，可以使抽象的知識變得更加生動，使學生對對數函數的建構過程更加清晰，有助于深度學習的發生.同時，在此過程中，新、舊知識的對比，有利于實現知識、經驗和方法的遷移，有利于學生分析和解決問題能力的提升，促成高階思維的課程目標的達成.

總之，數學是一門邏輯性較強的學科，在課堂教學中，教師要重視引導學生將相關知識聯系起來，以此加深學生對新知的理解和掌握，優化原有的認知結構，發展學生數學核心素養.

（三）創設問題情境，提升數學體驗

數學知識是抽象的，若課堂教學僅依賴于教師的講授，則很容易使學生產生厭學情緒，影響其參與課堂的積極性、主動性，這樣深度學習也就無從談起.為了改變這一局面，讓學生全身心地投入數學學習中，教師不妨創建情境，將抽象的數學知識置于生動的問題情境中，讓學生在情境互動中理解知識的本質與意義，讓深度學習自然而然地發生.

例如，在教學“等比數列前n項和公式”時，為了提升學生的數學體驗，讓學生全身心投入和沉浸其中，教師根據學習內容的特點、教學目標的要求和學生思維發展水平創設了如下情境：國王想打賞象棋發明者，于是問他想要些什么.象棋發明者說：“我不要金銀珠寶，只要您在棋盤的第一個小格賞我1粒麥子，第二個小格賞我2粒麥子，第三個小格賞我4粒麥子……以此類推，將棋盤中的64個格子擺滿.”試想，如果你是國王，你會答應他的要求嗎？這樣通過創設情境，有效地激發了學生的探究欲.為了解決這一問題，教師又從學生已有知識和已有經驗出發，精心設計如下問題進行引導：

（1）依據要求，你能算出每小格棋盤的麥粒數嗎？

（2）觀察數字，你發現了什么規律？它是等差數列還是等比數列呢？

（3）如果讓你計算一共有多少粒麥子，你想怎么算？

（4）你能幫國王算出麥粒數嗎？如果你是國王，你會答應嗎？

（5）請結合以上探究過程總結歸納等比數列前n項和公式.

教學中，教師先是創設有趣的情境激發學生的探究欲，然后巧妙地設計問題引導學生將其與等差數列相關知識相類比，由此開啟學生的高階思維，幫助學生順利推導出“等比數列前n項和公式”.通過經歷以上探究過程，學生充分體驗了成功的喜悅，真實感受了數學在解決現實問題中的價值，這有利于發展學生的邏輯推理、數學運算等核心素養.

（四）師生雙向互動，建立學習共同體

教學是教與學的交往、互動，沒有交往、沒有互動，也就沒有教學的發生.教學可以理解為是師生相互交流、相互補充、相互啟發的過程，也是師生雙方相互成就的過程.在深度學習過程中，教師要為學生搭建一個互動交流的平臺，讓學生主動表達自己的所思、所想，構建以學為中心的學習共同體，形成學習的內動力和積極的學習心態，讓學生學會學習.同時，教學中教師要樹立“學生”意識，善于從學生的視角思考和解決問題，為學生的思維牽線搭橋，讓學生學有所獲，從而提升課堂教學質量.

例如，在雙曲線的應用中，教師給出了這樣一道題：已知A，B兩地相距900米，一枚炮彈在某地發生爆炸，B地聽到爆炸聲2秒后，A地才聽到爆炸聲，若聲速是340米/秒，試求爆炸點可能的位置.學生審題后，未能與雙曲線模型建立聯系，解題時遇到障礙.為了幫助學生突破障礙，教師與學生進行互動交流.

師：本題的關鍵條件是什么？

生1：B地聽到的爆炸聲比A地聽到的爆炸聲早2秒.

師：若將其轉化為數學問題，你想到了什么？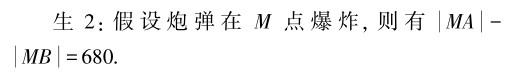

師：非常好，若M在A，B的連線上，則會是什么圖形呢？

由此通過“對話”，課堂“慢”了下來，學生逐漸認清了問題的本質，找準了解題方法，有效地突破了解題難點，增強了學生的解題信心.

深度學習強調主動理解，主動探索、主動感悟，因此當學生遇到障礙時，教師不要急于講授，應該適當放慢速度，通過“對話”為學生的思維搭橋，誘發學生深度思考，從而讓深度學習真正發生.

（五）創設有效問題，促進深度思考

問題是思維的起點，是發展學生高階思維的加速器.深度學習離不開深度思維，因此在課堂教學中，教師要創設一些能夠觸及學生心靈的、凸顯問題本質的、具有一定深度的問題，以此撬動學生的思維，促進學生深度思考.

例如，已知圓的方程為x2+y2=r2，點M（x0，y0）為圓上一點，求經過點M的切線方程.

在教師的指導下，學生積極思考，得到該切線方程為：x0x+y0y=r2.在此基礎上，為了增強學生的批判意識，教師設計了以下形同質異的變式題.

變式1 已知點M（x0，y0）是圓x2+y2=r2內的一點（點M異于圓心），試判斷直線x0x+y0y=r2與圓的位置關系.

從解題反饋來看，很多學生受原題影響，看到直

這樣有了前面問題的鋪墊，學生擺脫“想當然”的束縛，冷靜思考，通過遷移和轉化順利地解決了問題.

基于此，在實際教學中，教師要適當為學生創設一些“陷阱”，誘導學生犯錯，以此通過經歷析錯、糾錯等過程加深學生對知識的理解，增強學生批判意識，凸顯問題本質，實現深度學習.

總之，深度學習離不開深度教學.在實際教學中，教師應從教學實際出發，創設符合學生認知水平，能夠誘發學生思考，激發學生探究欲的教學活動，以此讓學生主動參與到課堂教學活動中，使學生學習逐漸走向深入，促進學生發展核心素養.當然，深度學習是一個長期的過程，需要學生進行長期堅持不懈的努力，因此教師要正視這個客觀規律，不斷更新教學觀念，優化教學結構，加強“學生”意識，努力構建學習共同體，不斷提高教學質量，切實提升學生數學核心素養.

【參考文獻】

[1]郭興甫.淺談數學教學中構建問題情境的策略[J].課程教材教學研究（中教研究），2004（Z5）：55-56.

[2]王延全.挖掘課本習題資源提升數學課堂效率[J].數學大世界（教師適用），2012（10）：67.

[3]杜金梅.試論高中數學課堂教學深度學習的有效實施[J].新課程（下），2018（11）：7.

[4]張曉祿.高中數學：從“知識教學”走向核心素養培育[J].數學教學通訊，2021（36）：44-45.

[5]洪明磊.促進深度學習的高中數學教學策略研究[J].數學學習與研究，2021（24）：127-128.