探究平面幾何證明思路的思維過程

【作者簡介】張昆，博士，副教授，中學高級教師。主要研究方向為數學教學論、數學史、數學教師教育、數學教育哲學。

【摘 要】本文通過“邊想邊說”與反思相結合的研究，發現在探究平面幾何證明思路時，學生的思維存在三個層次，其中思維的第二層次具有非常高的教學價值；一個班級中的學生存在著不同的認知方式，學生個體一般以自己的優勢認知方式理解情境中的信息，從而賦予信息以意義。因此，在探究平面幾何證明思路時，教師應通過教材分析與學情分析，選擇具體的思維層次的幾何證明題，平衡學生需要的認知方式，做好教學設計及課堂實施活動。

【關鍵詞】探究；思維過程；思維層次；平面幾何；“邊想邊說”；反思

開篇明義，本文要研究學生探究平面幾何證明題時的思維活動過程。那么，什么是數學思維呢？所謂數學思維，指的是在遇到數學情境、學習數學知識或解決數學問題時，學生為了應對其中的困境，他們的認知結構中所發生的心理活動。［1］這就將數學思維界定為一種狹義的個性心理活動，依據這一數學思維內涵，可以將數學思維過程界定為處理數學符號元素及符號元素之間互相作用的心理活動過程。［2］數學符號元素包括數學意象、數學概念和表示具體數學內容的語言（如漢語、英語等）、圖形、圖表等，數學符號元素及其互相作用是學習主體能夠調動、調整、控制甚至臨時自行創造出來的。

為了研究學生探究平面幾何證明思路的思維過程，以下先討論由數學思維及思維過程的內涵所決定的個體數學思維的三個主要層次。

一、學生探究平面幾何的思維層次

為了探究數學思維活動操作的心理過程，首先從對思維及其結構的譬喻展開認知。眾所周知，當人們在一件樂器上彈奏一個音時，在這件樂器可能發出的全部聲音中，只有這唯一的一個樂鍵發出來的那個音是現實的。同樣，當人在感知眼前的事物時，他規定的全部無限可能性就被限制在這唯一的存在方式上。因此，在只有這種沖動發生作用的地方，必然存在著最高程度的限制；人在這種狀態中只不過是一個數量的統一體，是時間的一個實現了的瞬間。［3］

由這個譬喻內容可以認識到，大腦中存在的思維瞬間相當于一件樂器上的一個按鍵，發動思維活動的某些物質性的要素，也會組成一個結構，我們將其簡稱為思維結構。因此，這里要考察探究平面幾何證明思路所需要動用的思維結構。由數學思維與數學思維過程這兩個概念所界定的內涵可以認識到，面對具體的數學問題，學生在應對問題所提供的具體信息時，會啟動思維并維持思維進展，這是大腦作為整體結構所支持的一種產生思維活動的思維結構。這種數學思維結構的構成成分，應該存在從具體逐步到抽象的三個主要層次。

1.第一層次

第一層次，具體數學問題中涉及的引發學生利用知識、方法等輔助思維的材料被立即激活。此時，對于探究某一具體的平面幾何證明思路，學生會審視問題信息的特點、已掌握的平面幾何知識內容（包括幾何概念、公理、定理、性質等）、數理邏輯（外在表現為問題信息中的因果關系，這種因果關系可內化為大腦中的相關對應物，如排序、包含、點數、空間等形式）［4］、所需要的證據（由幾何概念、公理、定理等已掌握的知識提供）、過去探究解題的方法與經驗等，這些都會對學生的探究思路起到啟發性作用，整個思維活動及過程都受到學生個體經驗中的這些要素的有價值的指導。

學生所掌握的平面幾何知識、方法、經驗、符號（或語言）等，為解決具體的平面幾何問題而展開的探究證明活動提供了啟發（如分析法與綜合法啟發證明思路），從而啟動思維，形成思維的定向，即思維活動的導向性軌跡等。這種導向性軌跡對于學生萌生有價值的證明思路具有非常重要的作用，也存在著學生個性數學思維的適應性（配合外在條件信息）的應用價值。因此，這種探究思路過程的思維是一種可觀察、可體悟的明晰的活動過程，思維的第一層次構成探究平面幾何證明思路的基礎性依靠。

2.第二層次

第二層次，相對于某個學生而言，面對平面幾何證明題的問題信息時，在思維的第一層次的某個或某幾個思維環節，利用已掌握與積累起來的知識、方法與經驗等處理數學符號（如幾何圖形，表示圖形的語言）元素及符號元素之間所應該構成的關系時，難以達到具體目的，也就是依據這些元素學生無法形成清晰的思維軌跡。學生對于這道平面幾何證明題所提供的外在信息（數學符號元素之間）只能進行外在現象的偶然搭配，探究有可能構成有意義（也有可能無意義）的輪廓結構。如此，學生處于認識的無目標、無順序之中。

思維的第二層次處于一種中間狀態。思維的第一層次的特點在于，學生能夠在充足的時間內自己探究出至少一條具體的證明思路，即能夠比較順利地從具體證明題的題設條件過渡到題斷結論。思維的第二層次的特點在于，學生在探究證明題的思路時不是一帆風順的，而是在從題設條件到題斷結論的某些環節上需要發掘隱含條件（不能通過僅觀察原問題的信息就能一眼看出的條件），需要在某個環節中架設起橋梁才能形成清晰的思維軌跡。

思維的第二層次應該是需要教師最為關注的地方。這是因為學生在教師精心的教學設計和課堂實施的啟發下，歷經艱難的思考活動，至少從體驗上感受到，經由自己思維力量（主體精神）的發揮，能在疑難環節上架設起證明思路所需要的橋梁。這是教師應該十分關注的地方，因為平面幾何證明題的教育教學價值主要體現在這些疑難環節上：一方面，這些疑難環節是教師培養學生思維能力的優質的教學素材，是學生能切身理解與體會的疑難所在，學習時具有極強的針對性；另一方面，當學生在教師的啟發下真真切切地突破了疑難環節，他們的學習情感就會得到極大的滿足，體會到思維活動的巨大潛力，如此，在面臨新問題時就會更集中注意力，維持思維就會更具持久性，力圖獨立完成探究活動的任務。

3.第三層次

第三層次，有的學生可能沒有完全理解題目提供的條件或結論所代表的具體意義，因此思維活動可能具有漫然性特點，對于問題所提供的條件或結論無法觸及。這種思維可能是從條件或結論的細枝末節中找到一種似是而非的支點，導致結果可能脫離條件或結論的本質信息，遠離題設條件或題斷結論的具體現實情境，更偏向于學生主觀的情感、想象。因此，這種思維無法獲得需要的結果。

即使如此，教師在教學設計及課堂實施中，對于思維的第三層次，也應該本著“取其精華、去其糟粕”的原則。在探究平面幾何證明思路時，教師在啟發學生的思維活動中必須處理好“虛”與“實”之間的關系。教師要認識到，思維的第三層次（思維已經處于比較“虛”的狀態）對于發展學生思維的創造性具有非常重要的作用，因為思維的創造性發揮可以幫助學生萌生重要的觀念。這種比較“虛”的思維活動雖然可能完全不顧及題目所設定的情境事實，但是在某種意義上依然存在思維對于問題信息的現實的適應性，從而引發學生對于題目所設定的現實產生一連串的思維活動，使得探究證明思路取得實際成效，特別是為突破疑難環節時所需要的創造性發揮提供精神“養料”。教師應該認識到教學要幫助學生體驗從“虛”到“實”的思維活動轉化過程。

4.思維三個層次的關系

基于以上分析，教師在教學設計及課堂實施時，需要特別關注第二層次的思維活動：在思維的第一層次中，即使沒有教師的教學啟發作用，學生也能按部就班或早或遲地找出證明的思路；思維的第二層次出現時，學生已經完成了思維的第一層次的探究活動并出現了疑難環節，因此教師需要引導學生突破疑難環節，將這些疑難環節轉化為優質的教學資源，引發學生的創造性思考，進一步發掘問題中的隱含條件。學生的思維能力在第二層次“真刀實槍”的思維活動過程中能更好地發展起來。

突破疑難環節的創造性思考，離不開第三層次思維的支持。當學生在客觀上設定的解題目標與探究解題思路處境中的某些環節之間存在鴻溝，學生經由不斷努力還是難以架設起橋梁時，就體會到過去習得的解題經驗與方法對于目前面臨的新問題無濟于事，這就使得學生的思考活動處于停滯狀態。此時，需要一些離問題情境較遠的自由想法，這些自由的想法中可能會有解決當前疑難問題的有價值的思維成果。思維的第三層次的作用就在于此。

總之，思維的三個層次具有互相作用的關系，因此，教師在教學設計及課堂實施中，應該以思維的第一層次為基礎，以思維的第二層次為教學重點與突破口，以思維的第三層次為創新活動的出發點，在備課時通過各個側面進入教學活動過程，盡可能多地找到解題途徑，仔細分析學生的思維水平與狀態，提高數學課堂教學的有效性。

二、學生實際思維活動過程

“邊想邊說”的研究方法雖然是一個研究學生數學解題思維活動的好方法，但這種方法也存在缺陷。因為從啟動與維持思維活動的本質上看，探究平面幾何證明思路所發起的絕大部分思維活動（特別是創造性想法的出現）是無意識的，所以盡管研究者想要學生說出真實的思考過程，但在某些思維的關鍵節點上往往難以實現。此時，就需要對學生突破疑難環節的成熟的思維活動過程進行反思，試圖從其所經歷的思維體驗中追溯過去實施的思維活動過程。

現舉一例來說明“邊想邊說”與反思相結合的方法，探究學生關于某一道平面幾何證明題思路的思維活動過程。

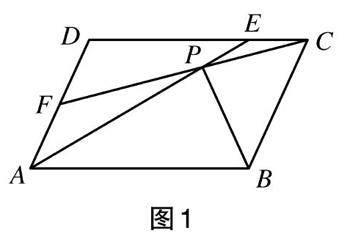
例1 已知：如圖1，在[?ABCD]中，AE=CF，AE與CF相交于點P，連接PB。求證：∠BPA=∠BPC。

師：記AE=CF為條件式①，∠BPA=∠BPC為結論式②，那么，如何探究證明結論式②的證明思路呢？

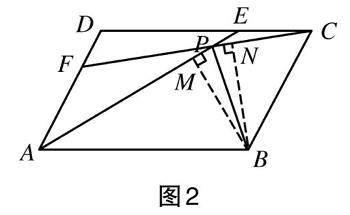
生1：在[?ABCD]這個框架中，條件式①沒有什么特別的，結論式②說明了線段BP是∠APC的平分線。要證明一條射線是一個角的平分線，可想到“到角的兩邊距離相等的點在這個角平分線上”這個定理。于是，過點B分別作BM⊥AE③交AE于點M，作BN⊥FC④交FC于點N（如圖2所示），現在證明BM=BN⑤這個過渡性的中間結論就能達到目的了。我想到證明Rt△BPMRt△BPN，但只能找到兩組對應的條件相等，可惜這兩個條件不能判定兩個三角形全等……（以省略號表示思維的暫時中斷，下同。）

【說明】從例子中學生“邊想邊說”的內容可以看到，學生目前處于思維的第一層次，即從題斷結論出發，將所要證明的結論式②轉化為證明過渡性結論式⑤。但是他遇到了第一個疑難環節，這就需要他發掘題意中的某些隱含條件來突破這個疑難環節，這道題的證明思路才能打通。

師：你想得很不錯了。你開頭就提出了“在[?ABCD]這個框架中”，說明在你的意識中存在希望將條件與結論構成整體性的心理意向。你認為這道題的條件式①是肯定成立的，所需要證明的過渡性結論式⑤也一定成立。那么，①與⑤在[?ABCD]這個框架中可以構成一個有意義的整體嗎？

生2：我感覺不到①與⑤如何才能構成一個有意義的整體……

師：仔細對照圖2，你能猜想出①②③④這些要素如何組成一個有意的輪廓嗎？

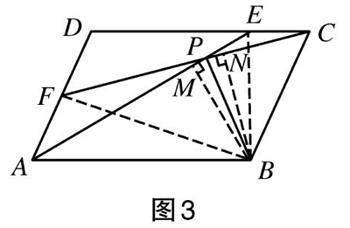
生3：我觀察圖2這個圖形，注意力逐漸集中于[?ABCD]這個框架中的條件BM⊥AE③與條件BN⊥FC④上，發現線段AB、線段AE和垂線段BM這三者之間沒有構成以一種有價值的輪廓（完整圖形的結構——筆者補充）。因此，我想到連接線段BE（如圖3所示），于是知道了線段BM是△AEB底邊AE上的高，因此，AE·BM=2S△BAE，而2S△BAE=[S?ABCD]⑥；同理，連接線段BF，可以得到CF·BN=2S△BCF=[S?ABCD]⑦。由等式⑥與等式⑦，知道等式AE·BM=CF·BN⑧成立，由條件式AE=CF①知過渡結論式BM=BN⑤成立，于是所要證明的結論式∠BPA=∠BPC②成立。

生4：因為①與⑤應該同時成立，現在我想將①與⑤集中起來構成一個整體性條件。集中的途徑是將①與⑤中的左右兩邊的兩條線段分別進行加減乘除運算，可以得到四個相關線段運算的等式，即AE+BM=CF+BN，AE-BM=CF-BN，AE·BM=CF·BN⑧，[AEBM]=[CFBN]。在這四個等式中，通過賦予其意義加以考察，由條件BM⊥AE③與條件BN⊥FC④，發現可以賦予等式⑧這個乘積式以三角形面積表達式的意義，其他三個等式都無法賦予意義。于是，將等式⑧兩邊都乘[12]，知等式[12]AE·BM=[12]CF·BN⑨應該成立。［5］（后續內容與生3類似，不再贅述。）

【說明】生3與生4在探究這道證明題時，使用了不同的思維方式。生3偏向于圖形直觀，由所作輔助線呈現的狀態直接看出可以利用三角形面積公式，而生4則偏向于運用已知條件或證明結論之間的關系所生成的集中條件的觀念，利用運算得到結果。

由“邊想邊說”與反思相結合的研究方法可以發現，在探究平面幾何證明思路時，學生的思維存在著三個層次，其中思維的第二層次具有非常高的教學價值。與此同時，一個班級中的學生存在著不同的認知方式，學生一般以自己的優勢認知方式理解情境中的信息，并賦予信息以意義。因此，在探究平面幾何證明思路時，教師應該通過教材分析與學情分析，選擇具體的思維層次（最為重要的是思維的第二層次）的幾何證明題，平衡學生需要的認知方式，做好教學設計及課堂實施活動。

參考文獻：

［1］張乃達. 數學思維教育學［M］. 南京：江蘇教育出版社，1990：4.

［2］克雷奇，克拉奇菲爾德，利維森，等.? 心理學綱要：上冊［M］. 周先庚，林傳鼎，張述祖，等譯. 北京：文化教育出版社，1980：188.

［3］席勒. 審美教育書簡［M］. 張玉能，譯. 南京：譯林出版社，2012：35.

［4］皮亞杰，英海爾德. 兒童心理學［M］. 吳福元，譯. 北京：商務印書館，1980：7.

［5］張昆，曹一鳴.完善數學教師教學行為的實現途徑［J］. 數學教育學報，2015（1）：33-37.

（責任編輯：潘安）