一種適用于復雜電網下的高精度鎖相環

摘 要：

針對現有并網逆變器在電網電壓諧波復雜的情況下難以精確鎖定電壓頻率和相位的問題，結合傳統鎖相環結構與自適應算法的理論提出一種高精度的鎖相方法。依據對傳統鎖相環在復雜電網下的弊端分析，確定了鎖相環采用傳統低通濾波器、帶通濾波器時的濾波效果與延時的矛盾關系。根據最小均方算法的高自適應特性與快速跟蹤特點，結合鎖相環中坐標變換公式，確定算法的輸入輸出以及權重矩陣，構建基于派克變換的最小均方算法矩陣模型。通過將所需的電壓正序分量設置為不斷更新的權重矩陣來進行高精度的濾波，同時通過引入均方瞬時誤差和自相關估計均值來進行變步長控制，提高濾波更新速度，以適用于復雜程度不確定的電網電壓進行自適應濾波鎖相。對仿真和樣機實驗的結果表明：采用基于派克變換的最小均方算法的改進型雙二階廣義積分鎖相方法，可以在不降低動態響應速度的前提下，提高鎖相環的濾波效果，進而提高并網逆變器在電網畸變嚴重場景下鎖定電壓頻率和相位的跟蹤精度。

關鍵詞：鎖相環；自適應濾波；雙二階廣義積分；最小均方算法；變步長

DOI：10.15938/j.emc.2024.03.005

中圖分類號：TM73

文獻標志碼：A

文章編號：1007-449X（2024）03-0043-13

收稿日期： 2023-02-28

基金項目：國家自然科學基金（51177037）

作者簡介：黃海宏（1973—），男，博士，教授，博士生導師，研究方向為電力電子技術與自動控制；

劉遠朋（1997—），男，碩士研究生，研究方向為電力電子與電氣傳動；

王海欣（1976—），女，碩士，高級工程師，研究方向為DSP應用技術。

通信作者：黃海宏

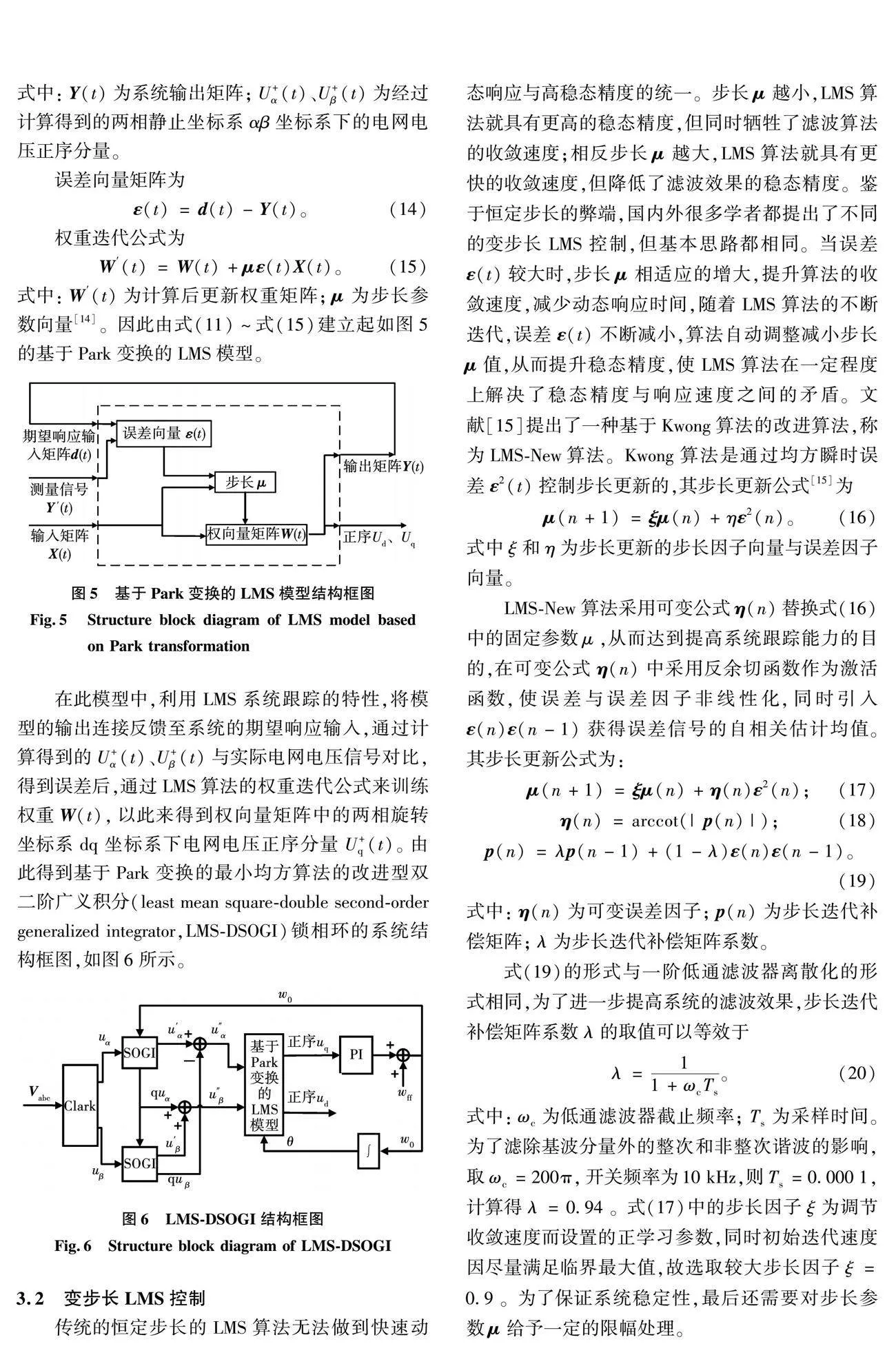
High-precision phase-locked loop suitable for complex power grids

HUANG Haihong， LIU Yuanpeng， WANG Haixin

（School of Electrical Engineering and Automation， Hefei University of Technology， Hefei 230009）

Abstract：

A high-precision phase-locked method was proposed by combining traditional phase-locked loops and adaptive algorithms to address the difficulty of accurately locking the voltage frequency and phase of existing grid connected inverters under complex grid voltage conditions. Based on the analysis of the drawbacks of traditional phase-locked loops， the contradiction between the filtering effect and delay when using traditional filters in phase-locked loops was determined. Based on the adaptive filtering characteristics of the minimum mean square algorithm and the coordinate transformation formula in the phase-locked loop， the input， output， and weight matrix of the algorithm were determined， and a minimum mean square algorithm matrix model based on the Parker transform was constructed. High precision filtering was achieved by setting the required voltage positive sequence component as a continuously updated weight matrix， while variable step size control was implemented by introducing mean square instantaneous error and autocorrelation estimation mean. The experimental results show that using an improved phase-locked method based on the minimum mean square algorithm can improve the filtering effect of the phase-locked loop without reducing the dynamic response speed， thereby improving the phase-locked accuracy of the grid connected inverter under grid distortion.

Keywords：phase locked loops; adaptive filtering; double second-order generalized integrator; least mean square; variable step

0 引 言

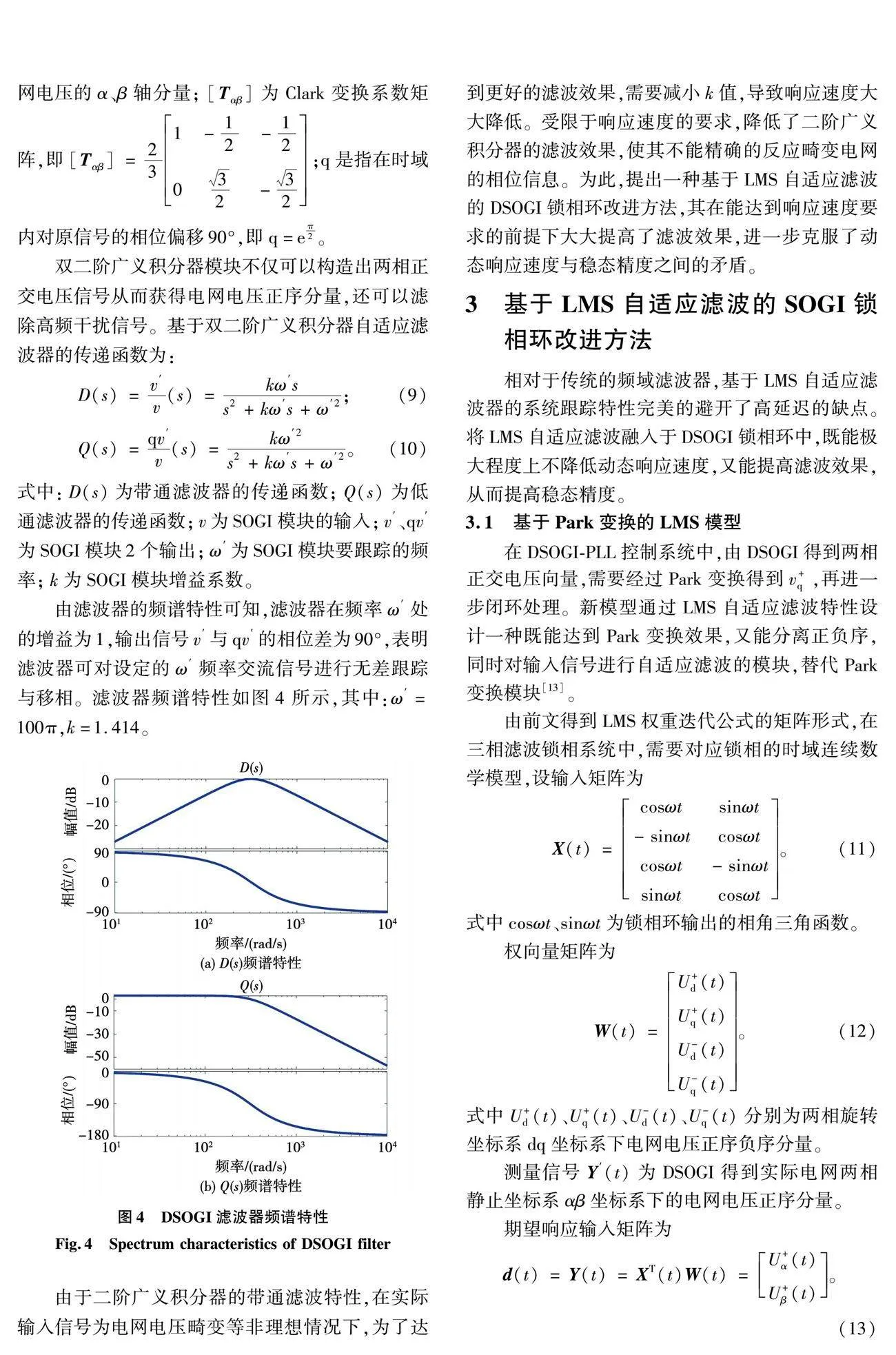
隨著新能源逆變器在電網的大規模接入，使得逆變器視角的電網等效阻抗隨之增加，導致電網電壓諧波含量增多且頻率發生變化，電網運行穩定性受到影響，電能質量下降［1-2］。傳統的基于雙二階廣義積分的軟件鎖相環（double second-order generalized integrator phase locked loops，DSOGI-PLL），是在產生2個用來分離正負序的正交信號的同時，利用基于內模原理的帶通濾波器來對電網畸變電壓進行諧波濾波。但在電網質量下降的情況下，如電網電壓不平衡、大量多次諧波疊加等非理想電網場合時，DSOGI-PLL鎖相難以滿足濾波要求。

目前，關于DSOGI-PLL控制改進方案，已有多篇學術論文進行分析報道，例如：

1）提出三階廣義積分器，通過在雙二階廣義積分器（double second-order generalized integrator，DSOGI）中增添一個積分單元，提高其架構單元的濾波效果。

2）提出一種在DSOGI前置特定次諧波消除模塊改進型鎖相環，通過前置模塊去除電網畸變電壓中畸變程度嚴重的特定次諧波，但系統增加低通濾波器會增加系統延時，降低了動態響應速度；且存在直流量時會產生周期干擾影響鎖相精度［3-4］。

3）提出一種多級并聯二階廣義積分器（multi-level second-order generalized integrator，MSOGI），通過構建多個具有對不同次數諧波濾波能力的SOGI模塊的并聯結構，在提高鎖相環對各次諧波分量的基礎上分離基波正序分量，但其結構太過復雜［5］。

4）提出一種二階廣義積分器的改進結構，構建求差節點消除直流量影響的同時，在求差節點前加入低通濾波器環節濾除高次諧波，在此基礎上加入頻率自適應環節，有很好的頻率跟蹤性能，但引入低通濾波器影響結構鎖相速度，且無法消除低次諧波影響［6-7］。

從前述現有技術的具體實現方式可知，為了減小負序分量的影響、取得較好的穩態精度，其中的環路濾波器的截止頻率必須取得很低，這極大地影響了動態響應的速度。

綜上，在特定場景下現有并網逆變器的鎖相技術難以精確鎖定電壓頻率和相位，故提出把基于派克（Park）變換的最小均方算法（least mean square，LMS）模型內嵌于DSOGI的拓撲結構改進方法，旨在提高并網逆變器在電網畸變嚴重場景下鎖定電壓頻率和相位的跟蹤精度，并通過理論分析、MATLAB仿真和樣機實驗，驗證了該改進方法的可實施性和濾波效果的有效性。

1 LMS自適應濾波原理

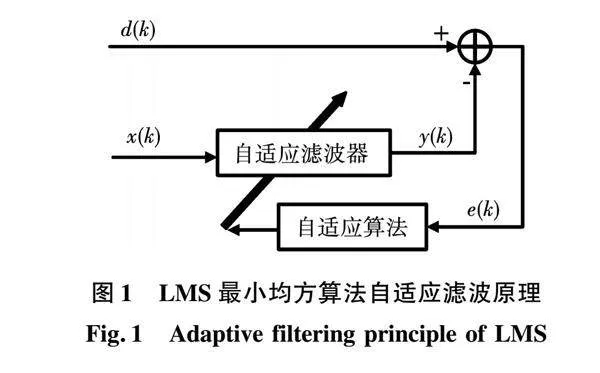
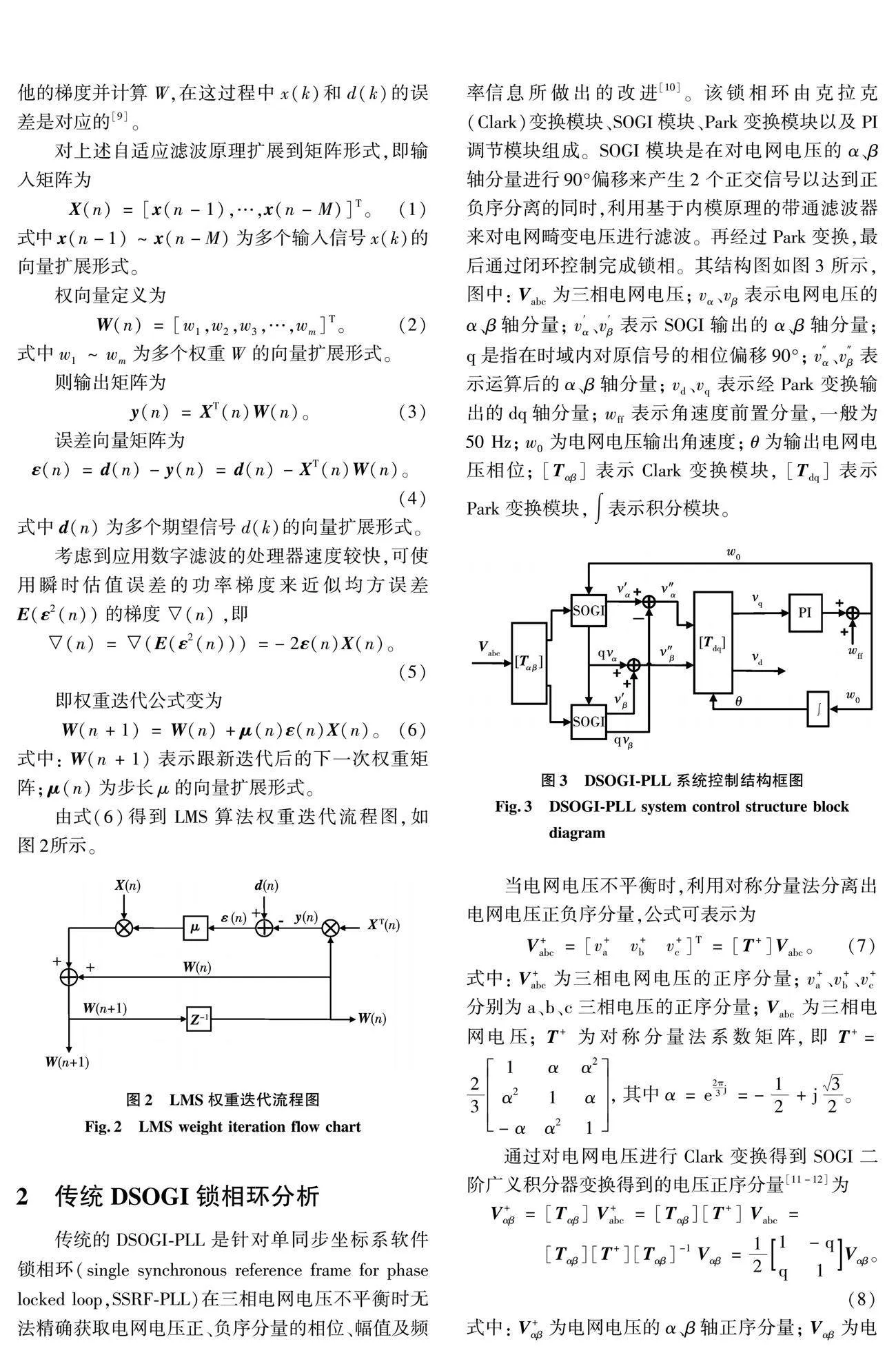
在通常的濾波場合中，從頻域的角度進行濾波，只要給出相應的設計指標就可以設計出滿足要求的濾波器。然而濾波器工作的環境是時變的，這就導致事先已經設計好的濾波器性能下降甚至不能被使用。自適應濾波算法中的LMS算法是基于維納濾波的算法，核心思想是梯度下降，用梯度矢量的估計值來代替其精確值。原理如圖1所示，其中輸入端信號x（k）、期望信號d（k）是自適應濾波器的2個輸入；輸出端信號y（k）、誤差信號e（k）是自適應濾波器的2個輸出［8］。

最小均方自適應濾波器在初始狀態下，濾波器權重系數設置為W（0），通過濾波器內部對輸入端信號x（k）進行相應計算，得到輸出端信號y（k），再將輸出端信號y（k）與濾波器的另外一路輸入信號期望信號d（k）進行比較，得到系統的誤差信號e（k），如果該誤差滿足均方誤差最小的判據，則不更新權重值；如果該誤差不滿足均方誤差最小的判據，則采用最小均方自適應優化算法去調節濾波器權重系數W。在多次的迭代計算后，得到系統的誤差信號e（k）最終將滿足均方誤差最小的判據，且此時權重系數由W（0）更新到W*。其中的權重優化算法為隨機梯度下降，即每進一個新數據x（k）求取他的梯度并計算W，在這過程中x（k）和d（k）的誤差是對應的［9］。

4 仿真與樣機驗證

4.1 系統仿真

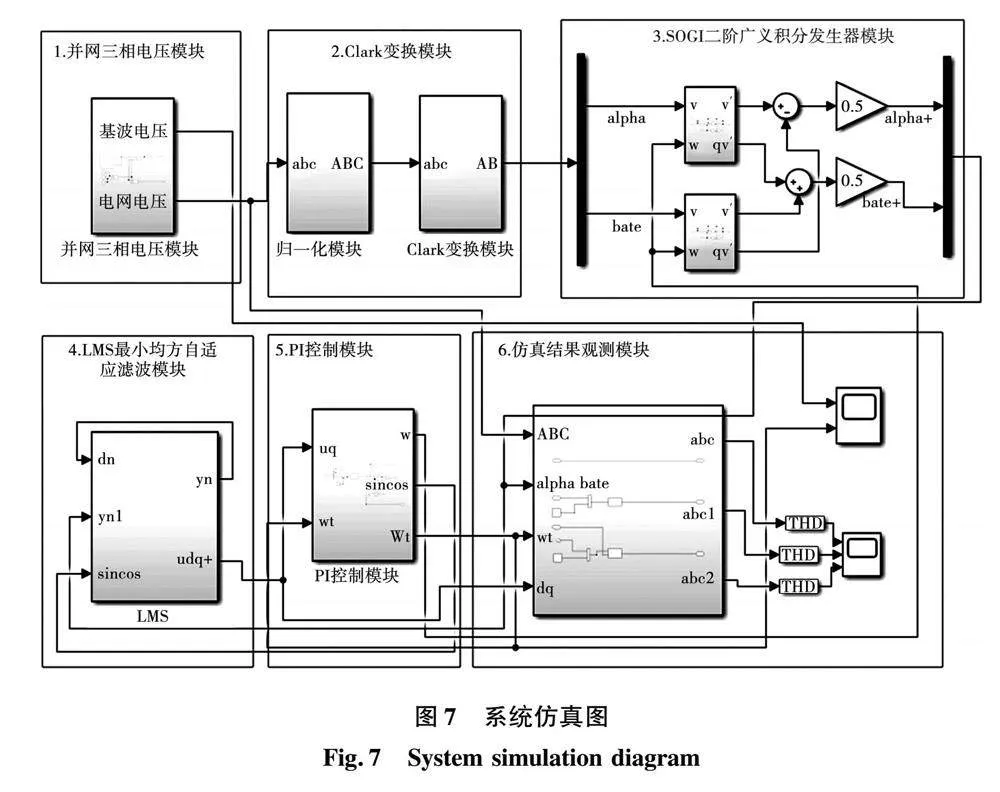
仿真框圖的搭建如圖7所示。其中包括并網三相電壓模塊、Clark變換模塊、SOGI二階廣義積分發生器模塊、LMS最小均方自適應濾波模塊、PI控制模塊、仿真結果觀測模塊。

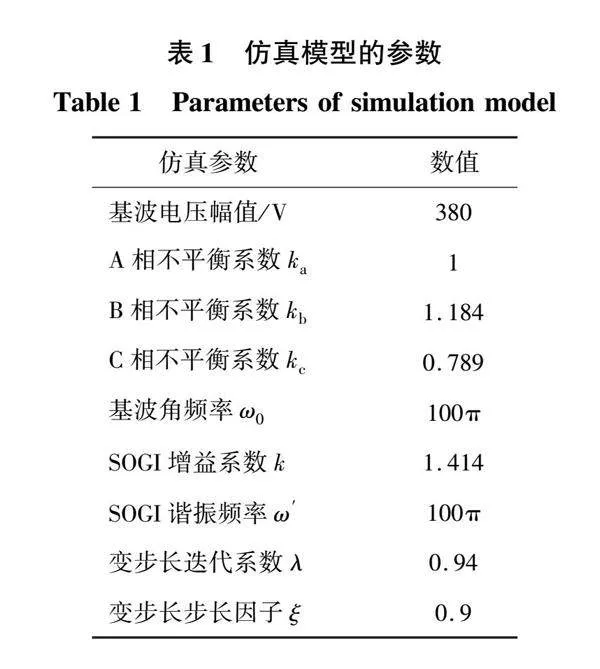
仿真模型的參數如表1所示。

仿真中在0～2 s與4～6 s為正常理想電網電壓階段，三相電壓為平衡的基波電壓UN；在2～4 s突變為含有幅值為基波電壓10%的2、4、5、7、10次諧波的不平衡三相電壓，其中三相不平衡系數如表1所示。分別對并網電壓、SOGI二階廣義積分發生器輸出電壓、LMS最小均方自適應濾波模塊輸出電壓統一變換為三相靜止坐標系abc坐標系下的電壓，再進行總諧波失真率（total harmonic distortion，THD）對比，分析其濾波效果。

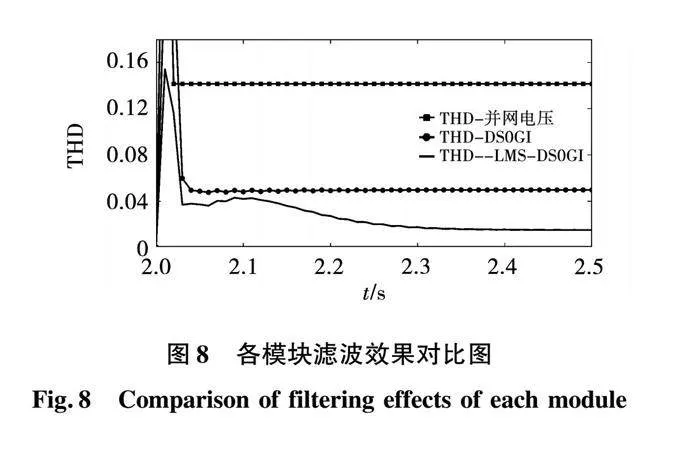
基于LMS自適應濾波的DSOGI系統各模塊濾波效果對比如圖8所示，其中方形實線表示并網電壓的THD，圓形實線表示SOGI二階廣義積分發生器模塊輸出電壓的THD，純實線表示LMS最小均方自適應濾波模塊輸出電壓下波形的THD。在仿真中0～2 s與4～6 s都是正常理想電網電壓階段，三者的THD穩態數值都接近于0；從圖8中可以看出在t=2.0 s后，由于電網電壓處于非理想電網階段，3個模塊濾波后的THD均發生躍變，在t=2.3 s后三者漸漸進入穩定狀態，其穩定狀態的THD值如圖所示，即三者穩態數值分別為并網電壓波形的THD=14.14%，SOGI濾波后電壓波形的THD=4.98%，LMS濾波后電壓波形的THD=1.55%。

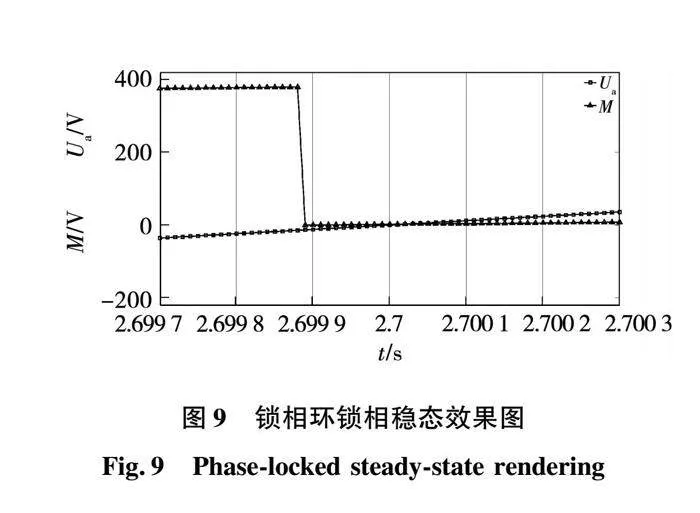
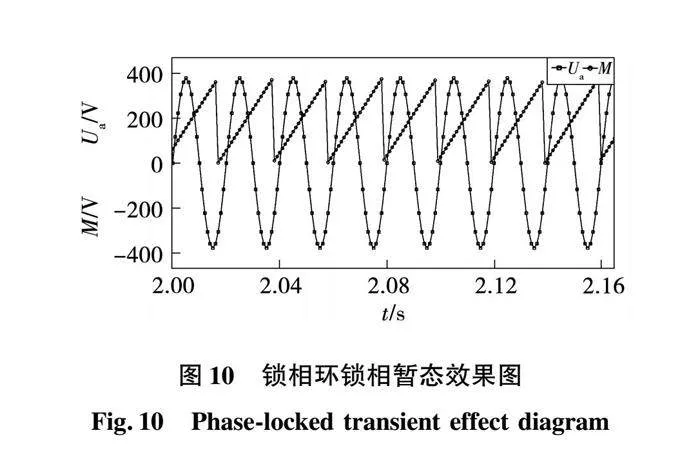
非理想電網下三相電網電壓自適應濾波鎖相環輸出的鎖相穩態效果、暫態效果如圖9與圖10所示。圖中：Ua表示電網基波電壓；M表示鎖相輸出角度，M的值為0～380 V，線性的對應電壓相位從0到2π。其中鎖相穩態效果圖取2～4 s非理想電網階段的2.699 7～2.700 3 s，由圖中的放大圖讀數可以得到鎖相穩態誤差為101.364 μs，約0.50%；鎖相暫態效果圖取2.0～2.165 s，是電網電壓由理想狀態轉向非理想狀態的過度階段，其過度轉折點為t=2 s時間點，即非理想階段的起點，LMS-DSOGI采用變步長設計后，約在t=2.16 s達到鎖相穩態，故其鎖相環的動態響應時間約0.16 s。

由此可見LMS-DSOGI鎖相環的濾波效果在SOGI的基礎上顯著提升，達到了預期目標，鎖相暫態效果在符合動態響應速度條件下，進一步降低了穩態誤差，符合前文理論分析。相較于傳統的DSOGI鎖相環，基于LMS自適應濾波的DSOGI系統在動態性能和穩態性能上都得到了改善。

4.2 樣機驗證

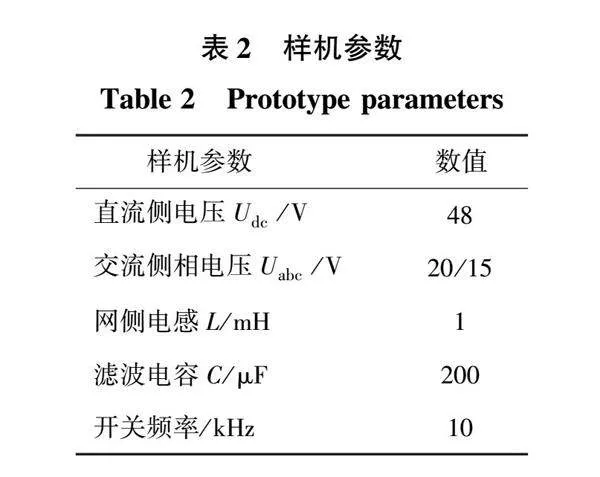
實驗采用低壓三相三線制逆變器樣機，樣機參數如表2所示。

樣機實驗采用TMS28335芯片進行數字控制，在代碼中設定鎖相輸出角度每次到2π時清零，同時在GPIO口產生一個翻轉信號，從而在示波器上展現鎖相的穩態與暫態效果。

電網電壓諧波的產生因素有很多，通常可以分為非線性負荷和逆變負荷這兩類。非線性負荷產生工頻頻率的整數倍諧波，例如三相6脈波整流器產生的5、7次諧波，三相12脈波整流器產生的11、12次諧波。逆變負荷產生逆變頻率2倍的諧波，如2、4、8、10次諧波等。

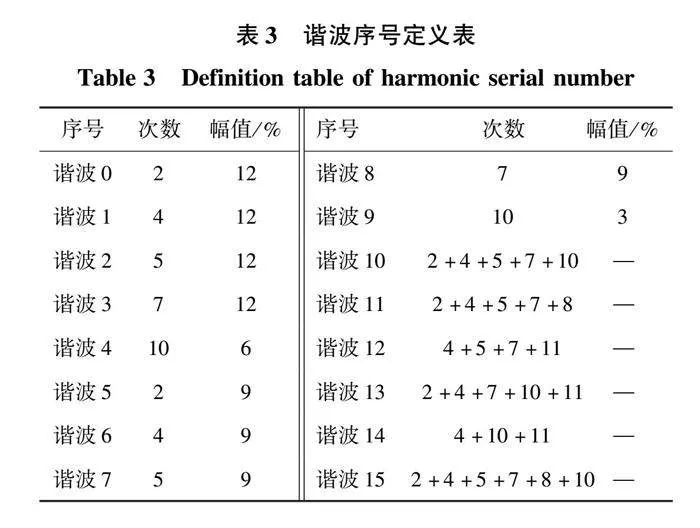
為了模擬電網電壓無規律的時變效果，本次樣機實驗在電網電壓基波中隨機注入上述單次諧波或多次諧波疊加，以便盡可能地模擬不同復雜程度的電網電壓。另外，本次實驗由可編程電源設備替代電網電壓，限于可編程電源設備的能力，因此注入的諧波次數與幅值也受限。注入的諧波如表3所示，其中定義的諧波0～諧波9為單次諧波，幅值為基波電壓的百分比；諧波10～諧波15為多次諧波疊加，其中2、4、5、7、8次諧波的幅值為基波電壓的12%，10、11次諧波的幅值為基波電壓的6%。

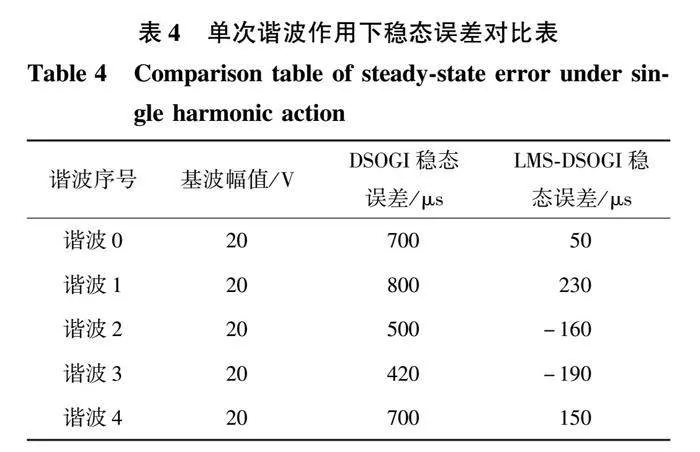
第一組實驗為傳統的DSOGI鎖相環與改進的LMS-DSOGI鎖相環在添加相同次數幅值諧波的畸變電網下的鎖相效果對比。單次諧波與多次諧波疊加作用下的穩態誤差數據如表4、表5所示。

由表4可以看出，傳統的DSOGI鎖相環在實驗設定的單次諧波電網下鎖相平均穩態誤差約為670 μs，即3.35%。且在注入低次諧波時，鎖相環的穩態誤差均很大；相較于傳統的DSOGI鎖相環，改進的LMS-DSOGI鎖相環在復雜畸變電網下的鎖相平均穩態誤差約為150 μs，即0.75%。

由表5可以看出，傳統的DSOGI鎖相環在實驗設定的復雜畸變電網下的鎖相平均穩態誤差約為700 μs，即3.5%。偶爾會出現穩態誤差很大的情況，導致鎖相環很大程度上不能穩定在700 μs的平均穩態誤差。相較于傳統的DSOGI鎖相環，改進的LMS-DSOGI鎖相環在復雜畸變電網下的鎖相穩態誤差約為200 μs，即1.0%。并且在相同的畸變電網作用時，不論其添加的諧波如何，改進的LMS-DSOGI鎖相環都比傳統的DSOGI鎖相環的鎖相穩態誤差要低得多，證明添加了LMS算法的改進型鎖相環能通過自適應濾波來提高從復雜電網畸變電壓中分離基波正負序的精確度，以此提升鎖相的精度。

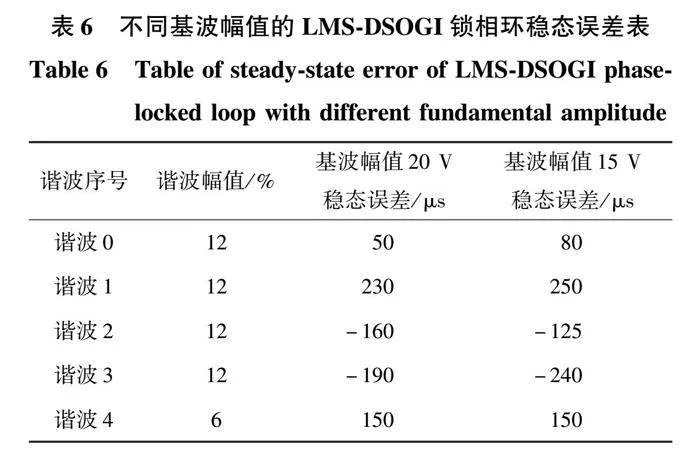
第二組實驗為改進的LMS-DSOGI鎖相環在添加相同次數幅值諧波的畸變電網下，不同基波幅值對鎖相效果的影響，穩態誤差數據如表6所示。

由表6可以看出，改進的LMS-DSOGI鎖相環在基波幅值15 V時的鎖相平均穩態誤差約為169 μs，即0.845%，相比于基波幅值20 V的150 μs（0.75%）平均穩態誤差有稍微的提高。隨著基波電壓增大，鎖相環采樣以及算法運算更為精確，以此降低了穩態誤差，提高鎖相精度。

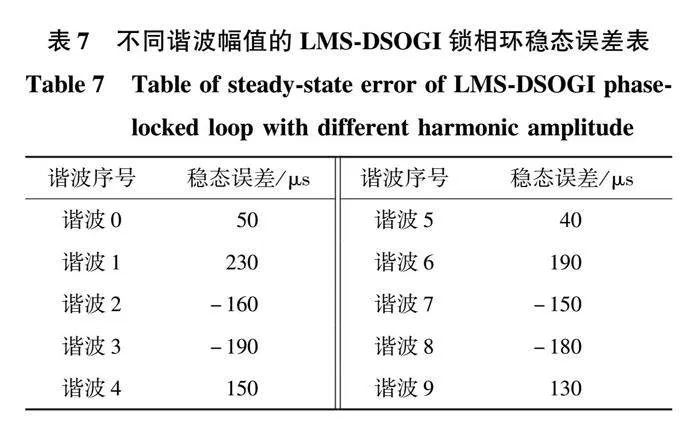
第三組實驗為改進的LMS-DSOGI鎖相環在添加幅值不同、次數相同的諧波畸變電網下的鎖相效果，穩態誤差數據如表7所示。

由表7可以看出，改進的LMS-DSOGI鎖相環在諧波為諧波5到諧波9時的鎖相平均穩態誤差約為138 μs，即0.69%，和諧波幅值更大的諧波0到諧波4作用下的150 μs（0.75%）平均穩態誤差幾乎相同。隨著添加諧波幅值的增大，電壓的畸變程度也越來越大，改進的LMS-DSOGI鎖相環中采用LMS自適應濾波部分同時也會根據所采樣的電壓進行自適應濾波，使鎖相環能夠穩定輸出精確度更高的鎖相角度，大大削弱了電網電壓不停變化的復雜諧波對鎖相精度帶來的負面影響。

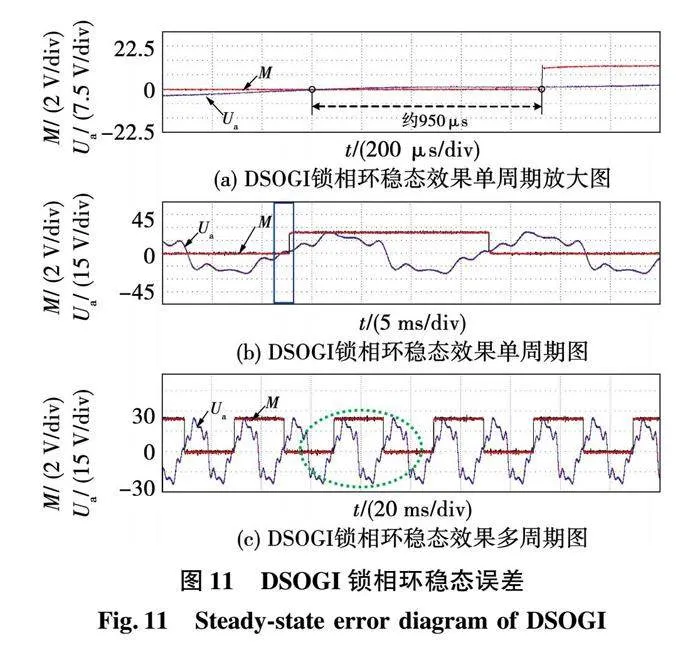
在上述的幾組實驗數據中畸變最嚴重的是在基波電壓上注入了諧波15的一組，即注入幅值為基波幅值12%的2、4、5、7、8次以及幅值為基波幅值6%的10次諧波的畸變電壓。傳統的DSOGI鎖相環在該畸變電壓下的穩態鎖相效果如圖11所示。

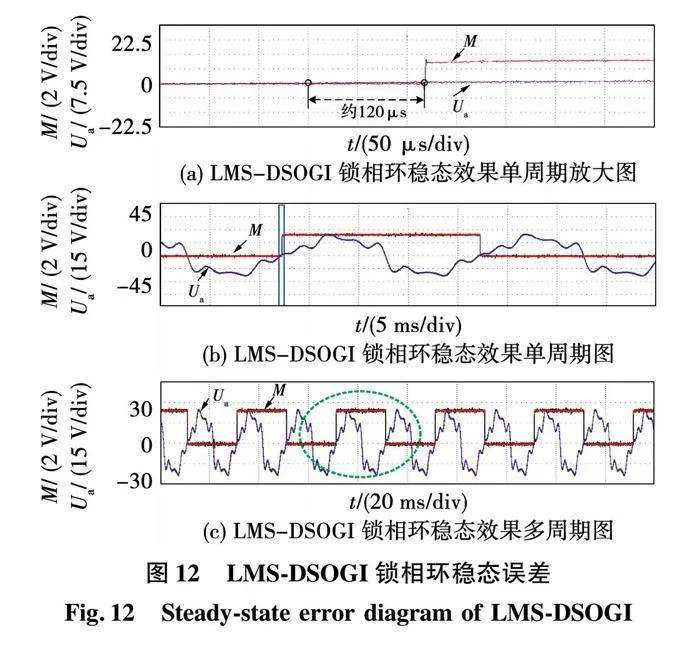
圖11（c）為DSOGI鎖相環多周期穩態效果展示圖；圖11（b）為圖11（c）中的虛線圓圈處一個周期的放大；圖11（a）為圖11（b）中矩形框處的放大展示圖。圖Ua表示電網A相畸變電壓波形；圖11～圖18中的M均表示鎖相效果翻轉波形，鎖相一個周波即翻轉一次。由圖中可以看出，穩態誤差約為950 μs。

改進的LMS-DSOGI鎖相環在該畸變電壓下的穩態鎖相效果如圖12所示，其中圖12（c）為改進的LMS-DSOGI鎖相環多周期穩態效果展示圖；圖12（b）為圖12（c）中的虛線圓圈處一個周期的放大；圖12 （a）為圖12（b）中矩形框處的放大展示圖。圖中的Ua表示電網A相畸變電壓波形。從圖中可以看出，穩態誤差約為120 μs。由此可見在電網電壓同樣復雜的情況下，改進的LMS-DSOGI鎖相環比傳統的DSOGI鎖相環穩態誤差更小，濾波效果更好，鎖相效果更精確。

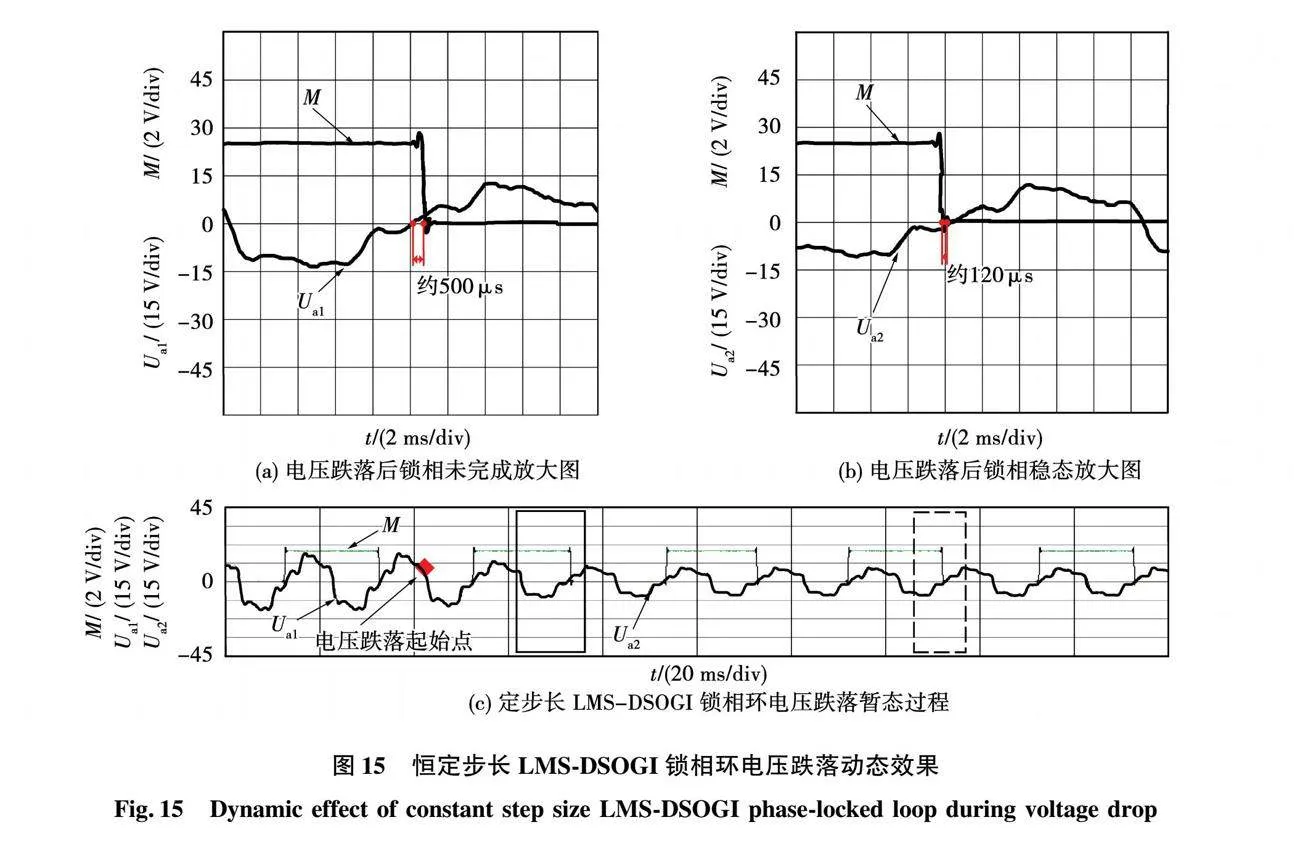
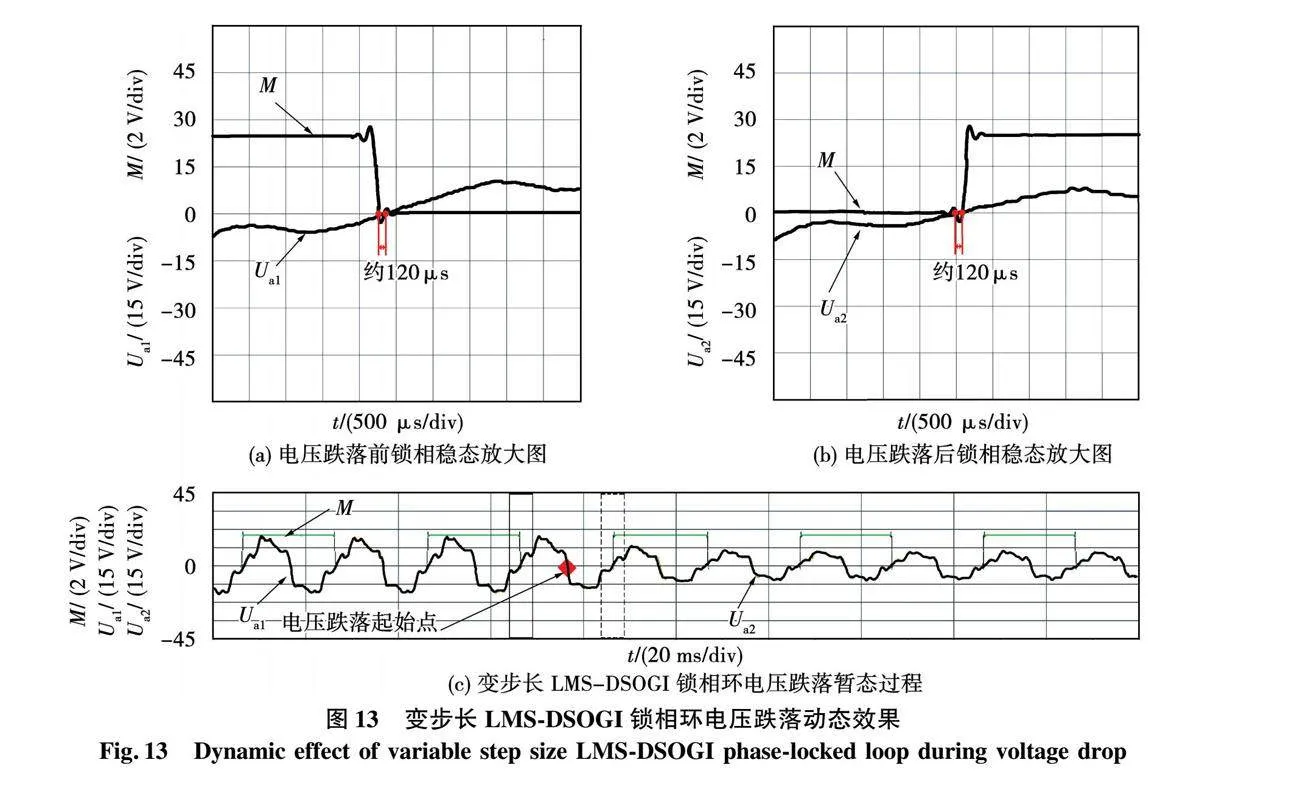
圖13～圖15為變步長LMS-DSOGI、DSOGI以及恒定步長LMS-DSOGI三種不同鎖相環在電壓跌落實驗中的暫態波形圖。

圖13、圖14的圖（a）和圖（b）分別為圖（c）在電壓跌落前（實線矩形框處）和電壓跌落后（虛線矩形框處）的鎖相穩態效果放大圖；圖15（a）為圖15（c）在電壓跌落后鎖相未完成（實線矩形框處）的放大圖，圖15（b）為圖15（c）在電壓跌落后的鎖相穩態（虛線矩形框處）效果放大圖。圖中Ua1和Ua2均為注入了幅值為基波幅值12%的2、4、5、7次以及幅值為基波幅值6%的10次諧波的A相畸變電壓，其中Ua1表示電壓跌落前基波電壓幅值為20 V的畸變電壓；Ua2表示電壓跌落后基波電壓幅值為10 V的畸變電壓。

在圖13中，電壓跌落前后一個周波的鎖相誤差約為120 μs，屬于改進的變步長LMS-DSOGI鎖相環的固有穩態誤差，故可以看作在電壓跌落后的一個周波，即20 ms就完成了鎖相動態過程。同樣在圖14中電壓跌落前后一個周波的鎖相誤差約為450 μs，也屬于傳統DSOGI鎖相環的固有穩態誤差，故也可以看作在電壓跌落后的一個周波，即20 ms就完成了鎖相動態過程。而在圖15中，電壓跌落后的一個周波鎖相誤差約為500 μs，與定步長LMS-DSOGI鎖相環的固有穩態誤差相差比較大，表明暫態過程未結束，直到電壓跌落后的第5個周波，鎖相誤差降為120 μs，才達到了定步長LMS-DSOGI鎖相環的固有穩態誤差要求，即鎖相動態過程需要100 ms。

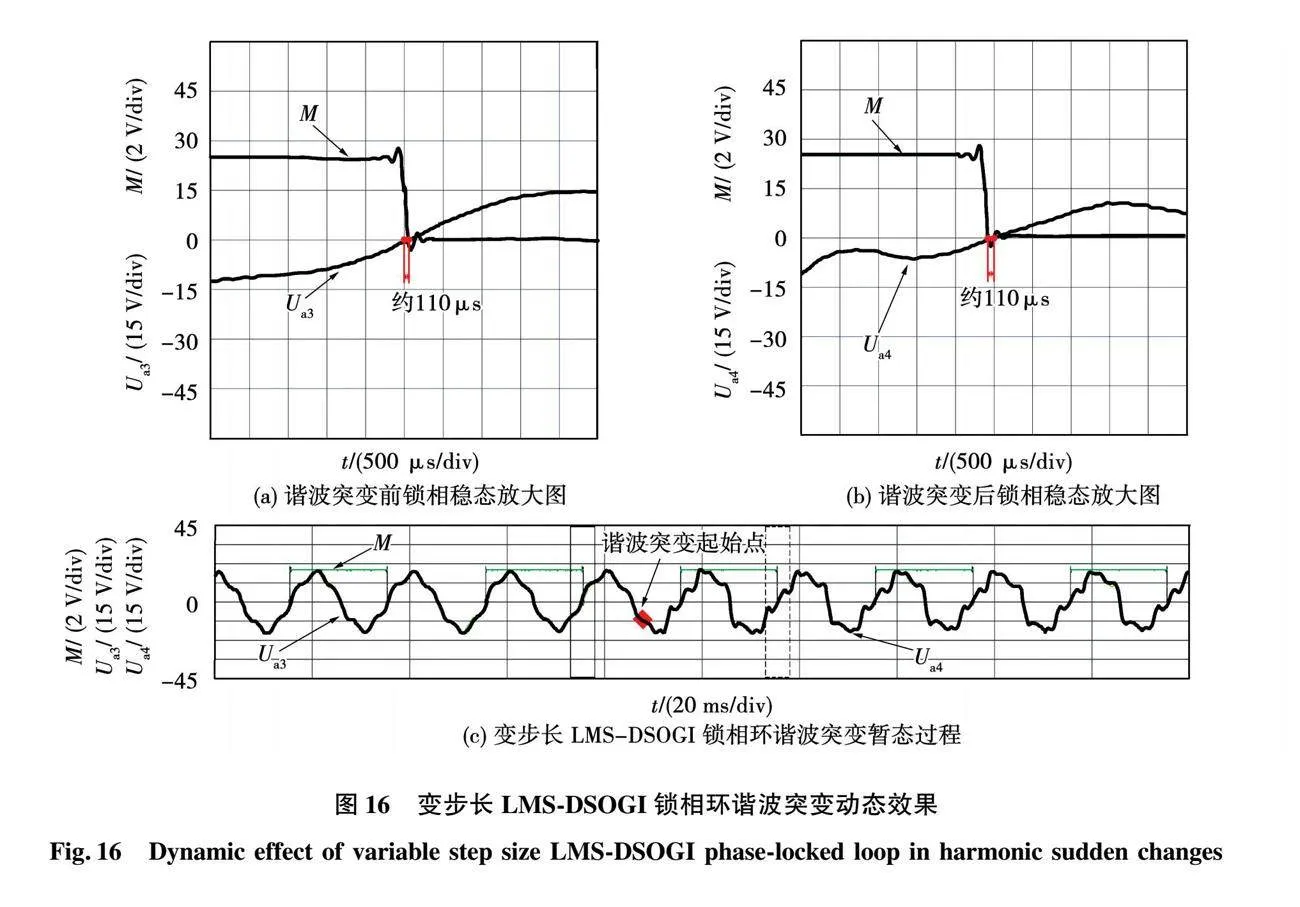
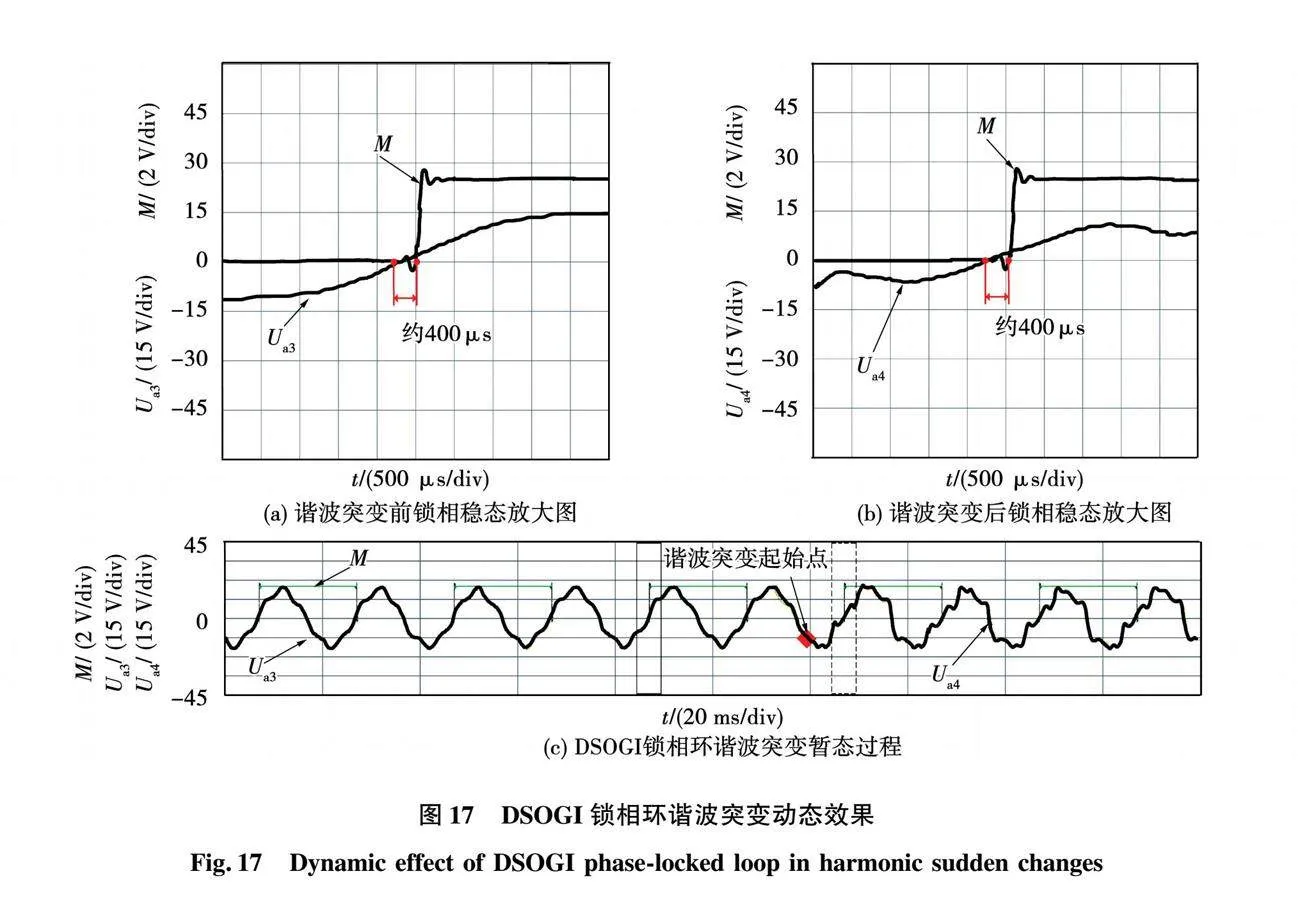
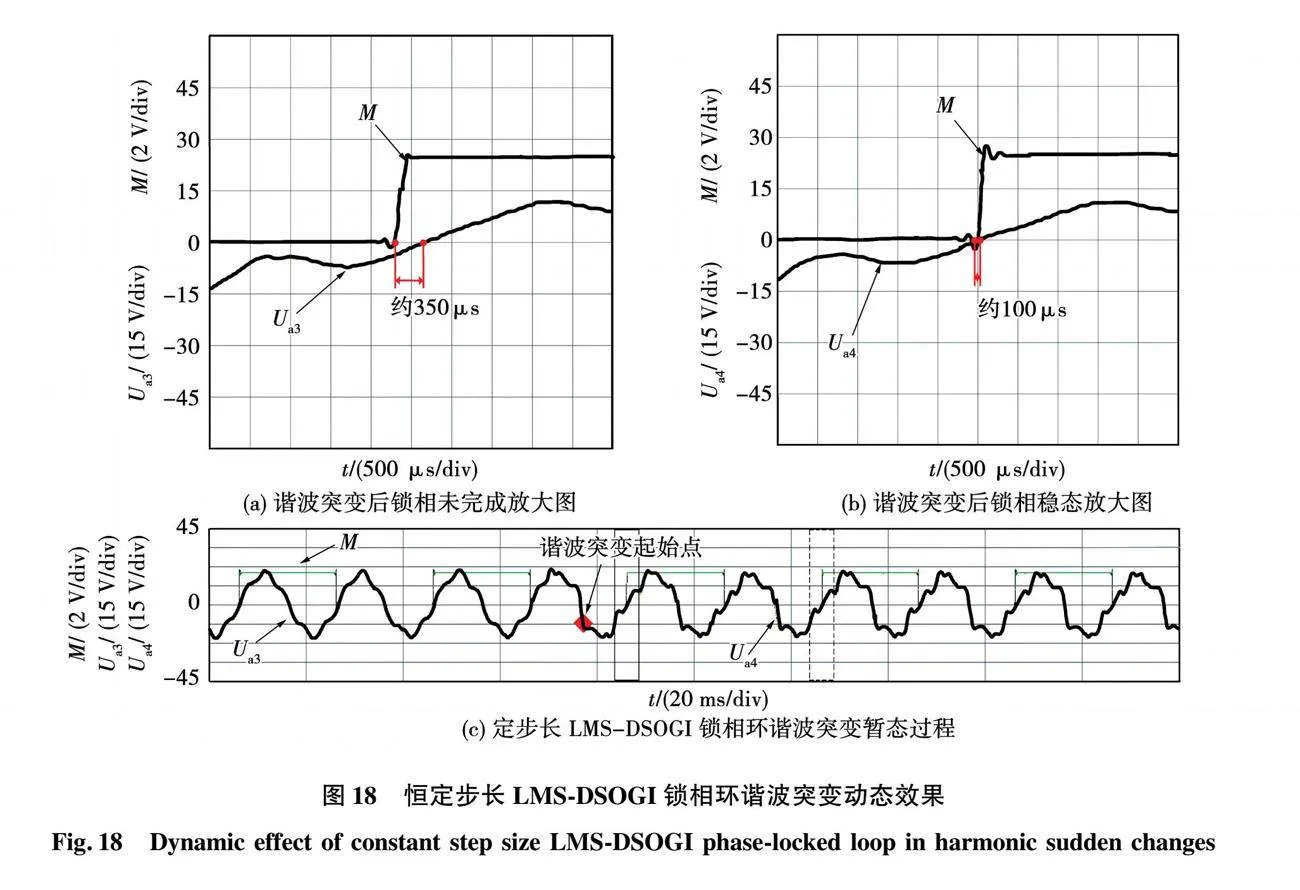
圖16～圖18為上述3種不同鎖相環在諧波突變實驗中的暫態波形圖。圖16、圖17的圖（a）和圖（b）分別為圖（c）在諧波突變前（實線矩形框處）和諧波突變后（虛線矩形框處）的鎖相穩態效果放大圖；圖18（a）為圖18（c）在諧波突變后鎖相未完成（實線矩形框處）的放大圖，圖18（b）為圖18（c）在諧波突變后（虛線矩形框處）的鎖相穩態效果放大圖。圖中Ua3和Ua4均表示基波電壓幅值為20 V的電網A相畸變電壓，其中Ua3注入了幅值為基波幅值12%的5次諧波；Ua4中注入了幅值為基波幅值12%的2、4、5、7次以及幅值為基波幅值6%的10次諧波。

在圖16中，諧波突變前后一個周波的鎖相誤差約為110 μs，屬于改進的變步長LMS-DSOGI鎖相環的固有穩態誤差，故可以看作在諧波突變后的一個周波，即20 ms就完成了鎖相動態過程。同樣在圖17中諧波突變前后一個周波的鎖相誤差約為400 μs，也屬于傳統DSOGI鎖相環的固有穩態誤差，故也可以看作在諧波突變后的一個周波，即20 ms就完成了鎖相動態過程。而在圖18中，諧波突變后的一個周波鎖相誤差約為350 μs，與定步長LMS-DSOGI鎖相環的固有穩態誤差相差比較大，表明暫態過程未結束，鎖相動態過程未完成，直到諧波突變后的第3個周波，鎖相誤差降為100 μs，達到了定步長LMS-DSOGI鎖相環的固有穩態誤差要求，才能視為動態過程結束，即60 ms才完成了鎖相動態過程。

由電壓跌落與諧波突變兩組實驗可以得到結論，定步長LMS-DSOGI鎖相環相比傳統DSOGI鎖相環雖然在鎖相精度上大幅度提高，但大大犧牲了動態響應速度；而變步長LMS-DSOGI鎖相環可在定步長高鎖相精度的基礎上提高動態性能，幾乎能達到傳統DSOGI鎖相環的動態性能。

5 結 論

基于Park變換的LMS模型的改進型DSOGI鎖相環比傳統的DSOGI鎖相環在相同響應速度的前提下具有更小的穩態誤差，內嵌的基于Park變換的LMS模型具有獨特的自適應濾波效果，使鎖相環具有較高的精確度及穩定性。進而提出的變步長LMS控制使動態響應速度大大提升，進一步克服了動態響應速度與穩態精度之間的矛盾。通過理論分析、系統仿真和樣機實驗，證明了改進型DSOGI鎖相環比傳統DSOGI鎖相環具有更好的穩態誤差和動態性能。

參 考 文 獻：

［1］ 黃海宏， 張庭茂， 魏亞坤， 等. 電壓不平衡時單同步坐標系鎖相環的改進算法［J］.電子測量與儀器學報， 2016， 30（6）： 937.

HUANG Haihong， ZHANG Tingmao， WEI Yakun， et al.Improved algorithm for phase-locked loop of single synchronous coordinate system under unbalanced three phase voltage［J］. Journal of Electronic Measurement and Instrument， 2016， 30（6）： 937.

［2］ 阮鵬， 吳趙風， 田剛領， 等. 非理想電網下三相逆變器的鎖相方法研究［J］. 電氣傳動， 2022， 52（2）： 45.

RUAN Peng， WU Zhaofeng， TIAN Gangling， et al. Research on the phase-locking method for three-phase inverters under non-ideal grid conditions［J］. Electric Drive， 2022， 52（2）： 45.

［3］ 涂娟， 湯寧平. 基于改進型DSOGI-PLL的電網電壓同步信號檢測［J］. 中國電機工程學報， 2016， 36（9）： 2350.

TU Juan， TANG Ningping. Synchronizing signal detection for grid voltage based on modified DSOGI-PLL［J］. Proceedings of the CSEE， 2016， 36（9）： 2350.

［4］ 劉啟德， 王海云， 王浩成， 等. 基于濾波器前置的三相軟件鎖相環設計［J］. 電力自動化設備， 2021， 41（7）： 124.

LIU Qide， WANG Haiyun， WANG Haocheng， et al. Design of three-phase software phase locked loop based on prefilter［J］. Electric Power Automation Equipment， 2021， 41（7）： 124.

［5］ RODRGUEZ P， LUNA A， CANDELA I， et al. Multiresonant frequency-locked-loop for grid synchronization of power converters under distorted grid conditons［J］. IEEE Transactions on Industrial Electronics， 2011，58 （1） ：127.

［6］ 黃海宏， 魏陽超， 王海欣， 等. 特定次諧波濾除鎖相在有源電力濾波器中的應用［J］. 電力自動化設備， 2019， 39（12）： 36.

HUANG Haihong， WEI Yangchao， WANG Haixin， et al. Application of specific harmonic filtering phase lock in APF［J］. Electric Power Automation Equipment， 2019， 39（12）： 36.

［7］ 李衛國， 劉宏偉， 劉新宇， 等. 基于改進SOGI-PLL的電壓同步信號檢測技術［J］. 東北電力大學學報， 2021， 41（3）： 93.

LI Weiguo， LIU Hongwei， LIU Xinyu， et al.Voltage synchronization signal detection technology based on improved SOGI-PLL［J］. Journal of Northeast Electric Power University， 2021， 41（3）： 93.

［8］ 馬琴， 裴鑫， 陳卯蒸， 等. 基于自適應濾波的干擾消除方法研究［J］. 天文學報， 2022， 63（3）： 33.

MA Qin， PEI Xin， CHEN Maozheng， et al.A research of RFI mitigation method based on adaptive filter［J］. Acta Astronomica Sinica， 2022， 63（3）： 33.

［9］ 張玉良， 吳偉陵， 田寶玉， 等. 基于自適應步長LMS算法的判決反饋均衡器研究［J］. 電路與系統學報， 2003（3）： 113.

ZHANG Yuliang， WU Weiling， TIAN Baoyu， et al. The study on decision feedback equalizer based on LMS algorithm with adaptive steps［J］. Journal of Circuits and Systems， 2003（3）： 113.

［10］ 劉華吾， 孫永恒， 胡海兵， 等. 諧波畸變電網下的單相同步旋轉坐標系鎖相環［J］. 電力系統自動化， 2016， 40（13）： 93.

LIU Huawu， SUN Yongheng， HU Haibing， et al. Single-phase synchronous reference frame phase-locked loop under harmonic distorted power grid condition［J］. Automation of Electric Power Systems， 2016， 40（13）： 93.

［11］ 周科， 劉伯鴻， 高峰陽， 等. 改進型雙二階廣義積分器鎖相環［J］. 電測與儀表， 2019， 56（17）： 135.

ZHOU Ke， LIU Bohong， GAO Fengyang， et al.Improved dual second-order generalized integrator PLL［J］. Electrical Measurement and Instrumentation， 2019， 56（17）： 135.

［12］ 張竣淇， 康朋， 田昊， 等. 基于二階廣義積分器的LCL型并網逆變器延時補償方法［J］. 電氣傳動， 2021， 51（22）： 15.

ZHANG Junqi， KANG Peng， TIAN Hao， et al. A delay compensation method based on SOGI of LCL-type grid-connected inverter［J］. Electric Drive， 2021， 51（22）： 15.

［13］ 郭文勇， 趙彩宏， 張志豐， 等. 基于EVSS-LMS算法的三相幅相鎖相系統［J］. 電力系統自動化， 2008（11）： 77.

GUO Wenyong， ZHAO Caihong， ZHANG Zhifeng， et al.A novel three-phase magnitude phase-lock loop system based on extended variable step size least mean square algorithm［J］. Automation of Electric Power Systems， 2008（11）： 77.

［14］ 李文江， 安麗， 劉爽. 增強型LMS自適應電網畸變電流檢測算法研究［J］. 電工電能新技術， 2014， 33（9）： 57.

LI Wenjang， AN Li， LIU Shuang. Improved LMS adaptive detection algorithm research in grid distortion current detection［J］. Advanced Technology of Electrical Engineering and Energy， 2014， 33（9）： 57.

［15］ 張展， 冷全超， 王維， 等. 基于反余切函數的變步長LMS諧波檢測算法［J］. 傳感器與微系統， 2022， 41（9）： 144.

ZHANG Zhan， LENG Quanchao， WANG Wei， et al. Variable step size LMS harmonic detection algorithm based on anti-cotangent function［J］. Transducer and Microsystem Technologies， 2022， 41（9）： 144.

（編輯：劉琳琳）