基于特征向量信息支持向量機的RC框架易損性曲線預測

周宇 駱歡

摘要：易損性曲線將結構破壞等級與地震動強度相關聯(lián)，能夠直觀地反映結構破壞的概率，但在建立易損性曲線的過程中需要大量的結構非線性時程分析結果，因而計算效率不高。機器學習方法已被證明能較好地解決這一問題，但當訓練數(shù)據(jù)的規(guī)模較大時，由于訓練過程涉及求解大規(guī)模逆矩陣致使計算效率依然低下。為此，本文提出了一種特征向量信息支持向量機（EILS-SVM）的新方法克服此類方法的不足。在大規(guī)模數(shù)據(jù)集下，EILS-SVM能夠篩選小規(guī)模子樣本建立低秩核矩陣。這使得其訓練過程只需求解小規(guī)模低秩矩陣的逆矩陣，進而極大提高計算效率。為了驗證EILS-SVM的準確性和高效性，基于16500個鋼筋混凝土（RC）框架在地震作用下的破壞數(shù)據(jù)，分別與支持向量機（LS-SVM）、隨機森林、神經網絡、線性判別分析（LDA）、貝葉斯作對比。結果表明，EILS-SVM 能準確預測 RC框架的易損性曲線，其計算效率最高能提升近27倍。

關鍵詞：鋼筋混凝土框架；易損性曲線；特征向量；支持向量機；機器學習

中圖分類號：TU973.2文獻標識碼：A文章編號：1000-0666（2024）03-0359-10

doi：10.20015/j.cnki.ISSN1000-0666.2024.0052

0引言

地震易損性分析用于預測不同地震強度下結構發(fā)生各級破壞的概率，對結構的抗震設計、加固和維修決策具有重要的應用價值（孫柏濤，張桂欣，2012）。易損性曲線描述了結構在給定地震動強度的情況下超過指定極限狀態(tài)的概率，是易損性分析中的關鍵內容。目前，易損性曲線的預測方法有多種（Lallemant et al，2015），如云圖法（于曉輝，呂大剛，2016；Jalayer et al，2017；Mattei，Bedon，2021）、增量動力分析（Incremental Dynamic Analysis，IDA）（呂大剛等，2011；薛成鳳等，2017；路沙沙等，2021；Pujari et al，2013；Vamvatsikos，Cornell，2002）、多條帶法（Multiple Sequence Alignment，MSA）（程詩焱等，2020；Fatimah，Wong，2021；Bradley，2010），等等。然而，這些方法都需要通過大量的非線性時程分析計算結構的地震響應結果，進而判斷結構在地震作用下的破壞狀態(tài)，計算成本高，導致易損性曲線預測的計算效率不高。因此，如何高效準確地預測結構的易損性曲線，進而量化評估結構的抗震性能成為結構工程和地震工程領域研究的熱點與難點問題。

機器學習（Machine Learning，ML）方法因其強大的數(shù)據(jù)擬合能力已被廣泛運用到結構和地震工程領域，彌補了傳統(tǒng)方法的不足。Mitropoulou和Papadrakakis（2011）將人工神經網絡（Artificial Neural Network，ANN）與增量動力分析結合提出了基于人工神經網絡的易損性曲線預測方法。Kiani等（2019）利用多條帶法的結果發(fā)展了一種基于機器學習分類模型的易損性預測新方法，并且比較了隨機森林、支持向量機、貝葉斯等6種分類模型的結構破壞狀態(tài)預測效果。Gentile 和Galasso（2020）利用高斯過程回歸建立了考慮建筑種類屬性的易損性預測模型。研究人員利用支持向量機（Support Vector Machine，SVM）結合時程分析得到的結構響應數(shù)據(jù)開發(fā)了建筑易損性預測模型（李浩瑾等，2013；Mahmoudi，Chouinard，2016；Sainct et al，2020）。以上結果表明，基于機器學習的分析方法既能保證較高的預測性能，又能極大地提高計算效率，這是因為機器學習方法能夠自適應地擬合訓練數(shù)據(jù)形成預測模型，無需執(zhí)行復雜的非線性有限元計算過程。通過建立的預測模型預測結構響應，本質上等同于矩陣與向量的乘積，因此計算效率高。然而，由于機器學習方法在訓練過程時需要求解由訓練樣本所構成的系數(shù)矩陣的逆矩陣，這使得當訓練樣本數(shù)據(jù)的規(guī)模較大時，不僅對計算機的內存需求高，且計算效率低下（James et al，2013）。因此，在大規(guī)模訓練樣本下，機器學習方法就會喪失高效性。

本文將Nystrom近似論（Charless et al，2019）中的特征值與特征向量理論和機器學習方法中的最小二乘支持向量機（Least Squares Support Vector Machine，LS-SVM）（Suykens et al，2000）相結合，提出了特征向量信息支持向量機（Eigenvectors-Informed Support Vector Machines，EILS-SVM）的方法，并從公開數(shù)據(jù)庫（Wang，Luo，2023）提取了4層、6層、8層不同規(guī)格RC框架結構的結構響應數(shù)據(jù)，形成了16 500個樣本數(shù)據(jù)，將EILS-SVM分別與LS-SVM等傳統(tǒng)機器學習模型進行對比。

1EILS-SVM的原理及易損性預測應用

1.1EILS-SVM數(shù)學模型構建

最小二乘支持向量機（LS-SVM）（Suykens，Vandewalle，1999）分類模型是一種較為常用的機器學習算法，其將支持向量機（Support Vector Machine，SVM）（Cervantes et al，2020）中求解二次規(guī)劃問題轉化成了求解線性方程組問題，極大地提高了SVM訓練過程的計算效率。其優(yōu)化問題如下所示：[KH*2D]

min∶Jp（ω，ξ）=[SX（]1[]2[SX）]ωTω+γ[SX（]1[]2[SX）]∑[DD（]N[]k=1[DD）]ξ2k[JY]（1）[KH*1D]

s.t.∶yk［ωTφ（xk）+b］=1-ξk，k=1，…，N[JY]（2）[KH*1D]

式中：ξk∈R是定義誤差變量的向量；γ為正則化參數(shù)；φ（xk）∈Rh是高維輸入向量，其中φ（·）∶Rd→Rh表示從d維到具有h維的高維度Hilbert空間的映射函數(shù)。其原始空間下的預測模型表達式為：

y（x）=sign［ωTφ（x）+b］[JY]（3）

由于高維輸入向量φ（xk）未知，因此由式（1）和（2）構成的優(yōu)化問題無法直接求解。為此，通過引入拉格朗日乘子αk∈R，構造式（1）和（2）的拉格朗日函數(shù)，并在對偶空間里進行求解。拉格朗日函數(shù)表達式為：

L（ω，b，ξk，αk）=Jp（ω，ξk）-∑[DD（]N[]k=1[DD）]αk{yk［ωTφ（xk）+b］+ξk-1}[JY]（4）

引入KTT條件求解方程式（4），可得到如下方程組：[KH*2/3D][JP3]

[JB（［][FK（W][BG（][BHDWG1*2，WK1，WK6*2，WK1，WK6*2W]0[]y1[]…[]yN[BHG2*2]y1[]K（x1x1）+[SX（]1[]λ[SX）][]…[]K（x1xN）[BHG1*2][][][XZ（135#][XZ）][][BHG2*2]yN[]K（xNx1）[]…[]K（xNxN）+[SX（]1[]λ[SX）][BG）W][FK）][JB）］][HJ4mm][JB（［][HL（1]bα1αN[HL）][JB）］]=[JB（［][HL（1]011[HL）][JB）］][JY]（5）[KH*2D]

式中：K（xk，xl）=φT（xk）φ（xl）為核函數(shù)（本文所采用的核函數(shù)為高斯核（RBF）函數(shù)），通過帶入核函數(shù)便可在對偶空間中得到模型參數(shù)α和b，其在對偶空間下的預測模型表達式如下：[KH*2/3]

y（x）=sign［∑[DD（]N[]k=1[DD）]αkykK（x，xk）+b］[JY]（6）[KH*2/3]

至此，通過對偶空間建立的預測模型便可用于預測新樣本數(shù)據(jù)所屬的類別。但是，LS-SVM在求解矩陣方程（5）時，涉及到求解系數(shù)矩陣的逆矩陣，其計算復雜度與訓練樣本的規(guī)模N有關，為O［（N+1）3］。當給定訓練樣本數(shù)據(jù){xk，yk}Nk=1的規(guī)模N較大時，求解這一大規(guī)模矩陣的逆矩陣就會變得極為耗時，造成模型訓練過程的計算效率低下。因此，當訓練樣本的規(guī)模N較大時，在LS-SVM標準框架下通過方程（5），在對偶空間下求解模型參數(shù)進而構建預測模型（6）就會變得尤為低效。而反觀原始空間下預測模型（3），其模型參數(shù)ω的維度與高維輸入向量φ（xk）的維度h有關，計算復雜度為O［（h+1）3］。因此，即使訓練樣本數(shù)據(jù){xk，yk}Nk=1的規(guī)模N較大，若φ（xk）的維度hN，在原空間中建立預測模型將比在對偶空間下建立預測模型更為高效。這是因為，當hN時，在原始空間建立預測模型的計算復雜度要遠遠小于對偶空間，即O［（h+1）3］O［（N+1）3］。為了能在原空間建立預測模型，需要顯示地構建非線性映射函數(shù)φ（·）的數(shù)學模型。然而，通常情況下φ（·）的數(shù)學模型無法顯示。

為了解決這一問題，本文采用Nystrom方法中特征值和特征向量理論（Girolami，2002）近似估計出高維輸入向量φ（xk），[WT]使得可以在原空間建立預測模型（3），進而解決LS-SVM在大樣本訓練數(shù)據(jù)集下預測模型訓練效率低下的問題。首先，將方程（5）中由RBF核函數(shù)構成的核矩陣記為Ω（N，N）∈RN×N，其中Ω（k，l）=K（xk，xl），k，l=1，…，N。根據(jù)Mercer定理（Girolami，2002），可得到如下表達式：[KH*2/3]

K（xk，xl）=∑[DD（]h[]i=1[DD）]λii（xk）i（xl）[JY]（7）[KH*2/3D]

式中：λi和i分別是特征值和相應的特征函數(shù)。這些特征值和特征函數(shù)與如下積分方程相關聯(lián)，其表達式如下：[KH*2/3]

∫K（xk，x）i（x）p（x）dx=λii（xk）[JY]（8）[KH*2/3D]

式中：p（x）表示大規(guī)模訓練樣本輸入變量xk的概率密度函數(shù)。在給定大規(guī)模數(shù)據(jù)集{xk，yk}Nk=1的條件下，假設輸入樣本xk，k=1，…，N之間服從獨立同分布。為了近似估計特征函數(shù)的積分方程，可從大規(guī)模訓練樣本數(shù)據(jù)中隨機抽取m個子樣本{xt，yt}mt=1（mN），用子樣本中的輸入變量xt近似p（x），進而達到稀疏化的目的。基于此，式（8）可通過如下表達式近似：[KH*2/3]

[SX（]1[]m[SX）]∑[DD（]m[]t=1[DD）]K（xt，x）i（xt）≈λii（x）[JY]（9）[KH*2/3]

通過從大樣本訓練數(shù)據(jù)集中選取的m個子樣本{xt，yt}mk=1可建立相應的核矩陣Ω（m，m），并對核矩陣進行特征值分解，可得到如下方程：[KH*2/3]

Ω（m，m）AΦ^U1（m×m）=AΦ^U1（m×m）AΛ^U1（m×m）[JY]（10）[KH*2/3D]

式中：Ω（m，m）∈Rm×m表示近似大規(guī)模核矩陣Ω（N，N）的稀疏化核矩陣；AΦ^U1（m，m）∈Rm×m，表示由Ω（m，m）的特征向量組成的矩陣；AΛ^U1（m×m）=diag（［Aλ^U11，…，Aλ^U1m］）∈Rm×m表示由Ω（m，m）的特征值組成的對角矩陣。

將式（10）中的矩陣進行向量分解，可得到如下表達式：[KH*2/3]

λi=[SX（]1[]m[SX）]Aλ^U1i，A^U1i=[KF（]m[KF）]Φti[JY]（11）[KH*2/3]

將式（11）帶到方程（9）中可得到第i個特征函數(shù)的表達式：[KH*2/3]

φi（x）≈[SX（][KF（]m[KF）][][FK（W1*2。1]Aλ^U1i[FK）][SX）]∑[DD（]m[]t=1[DD）]K（x，xt）AΦ^U1ti[JY]（12）[KH*2/3D]

將式（7）與式（12）結合可以得到φ（xk）中第i個元素與第i個特征函數(shù)之間的關系式：[KH*2/3D]

φi（xk）=[KF（][FK（W1*2/3。1]Aλ^U1i[FK）][KF）]i（xk）=[SX（][KF（]m[KF）][][KF（][FK（W1*2/3。1]Aλ^U1i[FK）][KF）][SX）]∑[DD（]m[]t=1[DD）]AΦ^U1tiK（xt，xk）[JY]（13）[KH*2/3]

根據(jù)式（13）即可求出非線性高維向量的顯性估計Aφ^G1（xk），其中Aφ^G1（xk）=［Aφ^G11（xk），Aφ^G12（xk），…，Aφ^G1m（xk）］。因此，基于估計的高維輸入變量Aφ^G1（xk），可利用最小二乘法直接求解由方程（1）和（2）構成的優(yōu)化問題，進而可求得原空間下預測模型（3）中的模型參數(shù)ω和b。其計算公式為：[KH*2/3]

[JB（［]ωb[JB）］]=（AΦ^U1TeAΦ^U1e+[SX（]Im+1[]γ[SX）]）-1AΦ^U1Tey[JY]（14）[KH*2/3D]

式中：Im+1為（m+1）×（m+1）的單位矩陣；y=［y1，y2，…，yN］T；AΦ^U1e是N×（m+1）特征增廣矩陣，具體形式如下：

AΦ^U1e=[JB（［][HL（4]Aφ^G11（x1）[]…[]Aφ^G1m（x1）[]1[][XZ（135#][XZ）][][]Aφ^G11（xN）[]…[]Aφ^G1m（xN）[]1[HL）][JB）］][JY]（15）

由方程（14）可知，本文所提出的EILS-SVM模型的計算復雜度與高維映射函數(shù)φ（xk）的維度m有關，為O（m3）。因為mN，所以O（m3）O（N3）。因此，從理論上分析，本文提出的EILS-SVM模型能顯著提高計算效率。此外，由于系數(shù)矩陣（AΦ^U1TeAΦ^U1e+[SX（]Im+1[]γ[SX）]）-1的規(guī)模為（m+1）且（m+1）N，因此EILS-SVM也能顯著降低對計算機內存的需求。

1.2EILS-SVM預測模型建立步驟

基于EILS-SVM的結構破壞狀態(tài)預測模型的建立步驟如圖1所示，具體分為以下8個步驟：

步驟1：建立結構響應數(shù)據(jù)庫，獲得不同地震強度和不同地震強度下結構的工程需求參數(shù)（Engineering Demand Parameter，EDP）所組成的樣本集{IMi，EDPi}ni=1。

步驟2：為樣本集{IMi，EDPi}ni=1中的每個樣本點提取對應的結構設計變量和地震動參數(shù)建立樣本信息數(shù)據(jù)庫。

步驟3：基于結構的EDP極限狀態(tài)閾值，將樣本信息數(shù)據(jù)庫中的每個樣本點按照EDP是否超過閾值分為兩類，從而構建大規(guī)模數(shù)據(jù)集{xk，yk }Nk=1。其中xk=［x1，x2，…，xd］為結構的設計變量和地震動參數(shù)組成的向量，yk∈{1，-1}為不同結構破壞狀態(tài)的類別標簽。

步驟4：將數(shù)據(jù)集劃分為訓練集與測試集。其中訓練集中的部分數(shù)據(jù)（支持向量）用來訓練預測模型，測試集的數(shù)據(jù)則用來預測結構破壞狀態(tài)。

步驟5：確定子樣本規(guī)模大小m（mN）。子樣本規(guī)模大小直接影響EILS-SVM的性能，m過小會導致EILS-SVM的預測精度較低，m過大則會增加模型的計算成本，降低計算效率。

步驟6：從訓練集中隨機抽取m個樣本作為支持向量用于訓練EILS-SVM模型。

步驟7：按照本文提出的EILS-SVM理論求解出模型參數(shù)ω和b，建立支持向量機原空間預測模型。

步驟8：將測試集數(shù)據(jù)輸入建立好的原空間預測模型，開展結構在不同地震動強度IMi下的破壞狀態(tài)的預測。

2大規(guī)模RC框架分類數(shù)據(jù)集的創(chuàng)建

本文采用公開數(shù)據(jù)庫（Wang，Luo，2023）中的數(shù)據(jù)集作為EILS-SVM模型的訓練數(shù)據(jù)。該數(shù)據(jù)集包含廣泛分布在我國各大、中、小城市的4層、6層和8層典型RC框架結構，具體數(shù)據(jù)信息可參閱Wang和Luo（2023）的文獻。該數(shù)據(jù)庫中的結構響應數(shù)據(jù)是通過OpenSees（Mazzoni et al，2006）平臺建立上述框架結構的有限元分析模型獲得的。其中，框架梁和柱采用基于力插值函數(shù)的梁柱單元來模擬，截面混凝土采用Concrete02單軸材料模型，約束混凝土采用Mander模型，鋼筋采用Hysteretic單軸材料模型。Hysteretic單軸材料模型不但能夠考慮應力和應變的捏攏效應，還能考慮基于能量的強度退化效應以及基于延性的剛度退化效應（Mazzoni et al，2006）。通過調整Hysteretic模型中控制基于能量的強度退化參數(shù)D，可以準確反映強震作用下由于延性RC框架中框架柱產生較大的側向變形使得縱筋發(fā)生屈曲，進而導致其出現(xiàn)強度退化現(xiàn)象。

在用于訓練的樣本數(shù)據(jù)集{xk，yk}Nk=1中，xk∈Rd為預測模型的輸入變量，該變量由結構的設計參數(shù)以及地震動參數(shù)組成（表1）；yk∈{1，-1}為結構的破壞狀態(tài)組成的輸出變量，當結構破壞狀態(tài)為倒塌時，yk=1，未倒塌時，yk=-1。各輸入變量的參數(shù)分布、輸入變量與輸出變量間的相關系數(shù)均在表1中列出。由表1可知，單一輸入變量與輸出變量之間的相關性不大，說明二變量之間的線性關系不成立，而利用機器學習方法建立二者之間的非線性映射關系更為合理。

由于原始數(shù)據(jù)集中的輸出變量為最大層間位移角（連續(xù)型變量），而非RC框架結構的破壞狀態(tài)（離散型變量），這使得原始數(shù)據(jù)集雖然適用于回歸問題的求解，但是無法直接用于分類問題的求解，也就無法適用于本文的研究。為了解決這一問題，本文根據(jù)《建筑抗震設計規(guī)范》（GB 50011—2010），將最大層間位移角0.02 rad作為判定結構倒塌狀態(tài)的閾值，該規(guī)范將0.02 rad的位移角定義為結構生命安全極限狀態(tài)和塑性極限狀態(tài)的參考點，廣泛用于評估和設計類似的鋼筋混凝土框架結構。考慮到規(guī)范的普遍適用性和在工程實踐中的驗證，本文將原始數(shù)據(jù)按照最大層間位移角是否超過0.02 rad作為分類依據(jù)，以此區(qū)分結構的倒塌和未倒塌狀態(tài)，最終形成16 500組適用于解決分類問題的數(shù)據(jù)集，即{xk，yk }16500k=1。以六層RC框架為例，圖2展示了數(shù)據(jù)集中RC框架結構在不同地震動強度（一階自振周期對應的譜加速度Sa）作用下的倒塌和未倒塌兩類狀態(tài)的分布情況。

3EILS-SVM模型性能分析

3.1子樣本大小對模型性能的影響分析

將數(shù)據(jù)集{xk，yk }16500k=1按7∶3的比例隨機劃分成訓練集與測試集，最終得到11 500個訓練集樣本和4 950個測試集樣本。LS-SVM模型將對全部11 500個訓練樣本進行訓練。分別從訓練集中選取100，200，…，1 200組子樣本代替全部的11 500個訓練樣本進行訓練。圖3a給出了EILS-SVM模型中預測準確率與子樣本規(guī)模大小的關系。由圖3a可知，隨著子樣本規(guī)模的增加，EILS-SVM預測準確率呈上升趨勢，當子樣本規(guī)模達到800時，曲線趨近平緩，當子樣本規(guī)模達到800后，EILS-SVM預測準確率隨著子樣本規(guī)模的增加提升不大。而且，圖3a說明了本文提出的EILS-SVM模型在訓練集和測試集上的準確率高且差異不大，證明了本文采用的21個輸入變量是合理的，可以使模型泛化性能好，且不會出現(xiàn)過擬合問題。由圖3b可知，EILS-SVM的計算時間隨著子樣本規(guī)模的增大而不斷增加。因此，當子樣本規(guī)模為800時，EILS-SVM模型能在保證較高的預測準確率的同時確保較短的計算時間。

3.2EILS-SVM模型與傳統(tǒng)機器學習模型對比

為了評估EILS-SVM模型的預測性能及泛化能力，筆者將其與其它5種傳統(tǒng)的機器學習模型——最小二乘向量機（LS-SVM）、隨機森林、神經網絡、線性判別分析（LDA）和貝葉斯模型進行比較。EILS-SVM模型采用隨機選取的800個子樣本進行訓練，而其它傳統(tǒng)機器學習模型則采用全部11 500個樣本進行訓練，然后將訓練后的不同的機器學習模型分別對測試集數(shù)據(jù)進行預測，以此對比不同機器學習模型的有效性和泛化能力。圖4給出了使用EILS-SVM模型與使用其它5種模型預測得到的建筑物破壞狀態(tài)的混淆矩陣。混淆矩陣是機器學習中用于評價分類精度的一種標準格式，它展示了真實分類結果與預測分類結果的關系。混淆矩陣的對角線上的元素代表了正確預測的樣本數(shù)量，對角線外的元素代表了錯誤分類的樣本數(shù)量。圖中混淆矩陣右下角區(qū)域代表了預測準確率，兩側百分數(shù)區(qū)域分別代表精度與召回率。由圖4和表2可知，EILS-SVM和LS-SVM模型的預測準確率明顯優(yōu)于其它4種機器學習模型。同時，盡管EILS-SVM使用了較少的800個子樣本，其準確率仍與使用全部11 500個樣本進行訓練的LS-SVM相近，且用時僅為LS-SVM的1/27，說明EILS-SVM在處理大規(guī)模數(shù)據(jù)集時的有效性。

3.3基于EILS-SVM模型的易損性曲線預測

為了展示EILS-SVM模型預測易損性曲線的能力，將6層RC框架（基本自振周期T1=1.07s）在不同退化參數(shù)（D=0.1、0.6和1.0）下對應的30條地震動記錄及其調幅后共計900個樣本作為測試集，剩余15 600個樣本作為訓練集，對比EILS-SVM模型和其它有限元方法生成的易損性曲線。

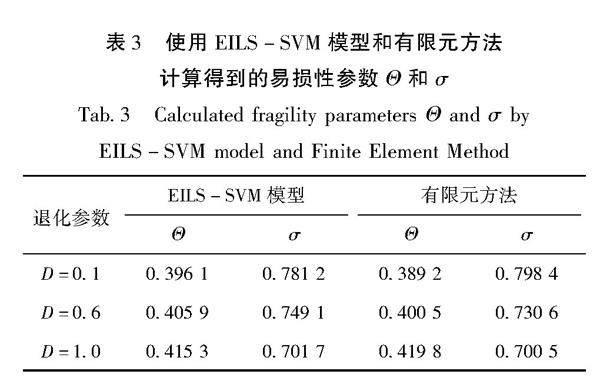
圖5給出了EILS-SVM模型對不同強度退化參數(shù)下6層RC框架破壞狀態(tài)的預測結果的混淆矩陣。從圖中可以看出EILS-SVM模型預測結果的正確率均達到了97%以上。用MSA方法（Baker，2015）分別計算出EILS-SVM模型和有限元方法的易損性參數(shù)θ和σ（表3）。圖6 分別給出了D=0.1、0.6和1.0時，通過EILS-SVM模型和有限元方法得到的易損性曲線。由圖6可看出，用EILS-SVM模型與用有限元方法預測的易損性曲線基本重合，表明EILS-SVM模型能夠準確預測RC框架的易損性曲線。

4結論

本文提出了特征向量信息支持向量機（EILS-SVM）模型，用于解決有限元方法計算結構易損性曲線時效率不高、大規(guī)模訓練樣本下傳統(tǒng)的機器學習訓練過程效率低下這兩個問題，并以RC框架的破壞狀態(tài)和易損性曲線預測為例，與傳統(tǒng)機器學習分類算法進行對比，結論如下：

（1）EILS-SVM模型的預測性能和計算效率與所選樣本子集規(guī)模有關，預測性能會隨著子集規(guī)模的增大而提高，但計算效率則會相應降低。

（2）與LS-SVM模型相比，當子集規(guī)模為800時，EILS-SVM模型的預測性能與基于11 550個大規(guī)模訓練樣本的LS-SVM模型的預測性能相當，且遠優(yōu)于隨機森林、神經網絡、線性判別分析（LDA）和貝葉斯算法。并且EILS-SVM模型的計算時間相較于傳統(tǒng)機器學習模型最高減少了27倍，顯著提高了計算效率。

（3）EILS-SVM模型能夠準確預測RC框架的易損性曲線，預測得到的易損性曲線與有限元方法生成的易損性曲線比較吻合。

參考文獻：

程詩焱，韓建平，于曉輝，等.2020.基于條帶-云圖法的地震動持時對結構地震易損性影響分析［J］.地震工程與工程振動，40（5）：107-117.Cheng S Y，Han J P，Yu X H，et al.2020.Investigation on effect of ground motion duration on seismic fragility of structures based on stripe-cloud approach［J］.Earthquake Engineering and Engineering Dynamics，40（5）：107-117.（in Chinese）

李浩瑾，李俊杰，康飛.2013.基于LSSVM的重力壩地震穩(wěn)定易損性分析［J］.振動與沖擊，32（4）：146-152.Li H J，Li J J，Kang F.2013.Analysis of seismic stability Fragility of gravity dam based on LSSVM［J］.Journal of Vibration and Shock，32（4）：146-152.（in Chinese）

路沙沙，徐紅，張亞楠，等.2021.基于IDA方法的加固震損RC框架結構地震易損性分析［J］.地震研究，44（4）：673-681.Lu S S，Xu H，Zhang Y N，et al.2021.Seismic fragility analysis of reinforced RC frame structure with seismic damage based on incremental dynamic analysis［J］.Journal of Seismological Research，44（4）：673-681.（in Chinese）

呂大剛，于曉輝，陳志恒.2011.鋼筋混凝土框架結構側向倒塌地震易損性分析［J］.哈爾濱工業(yè)大學學報，43（6）：1-5.Lyu D G，Yu X H，Cheng Z H.2011.Lateral seismic collapse fragility analysis of RC frame structures［J］.Journal of Harbin Institute of Technology，43（6）：1-5.（in Chinese）

孫柏濤，張桂欣.2012.汶川8.0級地震中各類建筑結構地震易損性統(tǒng)計分析［J］.土木工程學報，45（5）：26-30.Sun B T，Zhang G X.2012.Statistical analysis of seismic vulnerability of various building structures in Wenchuan M8.0 earthquake［J］.China Civil Engineering Journal，45（5）：26-30.（in Chinese）

薛成鳳，劉來君，武芳文.2017.大跨度混凝土梁斜拉橋橫向地震作用易損性分析［J］.地震研究，40（1）：65-69.Xue C F，Liu L J，Wu F W.2017.Fragility analysis of long-span concrete cable-stayed bridge under lateral seismic loads［J］.Journal of Seismological Research，40（1）：65-69.（in Chinese）

于曉輝，呂大剛.2016.基于云圖-條帶法的概率地震需求分析與地震易損性分析［J］.工程力學，33（6）：68-76.Yu X H，Lyu D G.2016.Probabilistic seismic demand analysis and seismic fragility analysis based on a cloud-stripe method［j］.Engineering Mechanics，33（6）：68-76.（in Chinese）

GB 50011—2010.建筑抗震設計規(guī)范［S］.GB 50011—2010.Seismic design of buildings［S］.（in Chinese）

Baker J W.2015.Efficient analytical fragility function fitting using dynamic structural analysis［J］.Earthquake Spectra，31（1）：579-599.

Bradley B A.2010.A generalized conditional intensity measure approach and holistic ground-motion selection［J］.Earthquake Engineering & Structural Dynamics，39（12）：1321-1342.

Cervantes J，Garcia-Lamont F，Rodríguez-Mazahua L，et al.2020.A comprehensive survey on support vector machine classification：Applications，challenges and trends［J］.Neurocomputing，408：189-215.

Charless F，Serge B，F(xiàn)an C，et al.2019.Spectral grouping using the Nystrom method［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，26（2）：214-225.

Fatimah S，Wong J.2021.Sensitivity of the fragility curve on type of analysis methods，applied ground motions and their selection techniques［J］.International Journal of Steel Structures，21（4）：1292-1304.

Gentile R，Galasso C.2020.Gaussian process regression for seismic fragility assessment of building portfolios［J］.Structural Safety，87：101980.

Girolami M.2002.Mercer kernel-based clustering in feature space［J］.IEEE Transactions on Neural Networks，13（3）：780-784.

Jalayer F，Ebrahimian H，Miano A，et al.2017.Analytical fragility assessment using unscaled ground motion records［J］.Earthquake Engineering & Structural Dynamics，46（15）：2639-2663.

James G，Witten D，Hastie T，et al.2013.An introduction to statistical learning：with applications in R［M］.Berlin：Springer Group.

Kiani J，Camp C，Pezeshk S.2019.On the application of machine learning techniques to derive seismic fragility curves［J］.Computers & Structures，218：108-122.

Lallemant D，Kiremidjian A，Burton H.2015.Statistical procedures for developing earthquake damage fragility curves［J］.Earthquake Engineering & Structural Dynamics，44（9）：1373-1389.

Mahmoudi S N，Chouinard L.2016.Seismic fragility assessment of highway bridges using support vector machines［J］.Bulletin of Earthquake Engineering，14（6）：1571-1587.

Mattei S，Bedon C.2021.Analytical Fragility Curves for Seismic Design of Glass Systems Based on Cloud Analysis［J］.Symmetry，13（8）：1541.

Mazzoni S，Mckenna F，Scott M H，et al.2006.Open system for earthquake engineering simulation user command language manual［M/OL］.University of California，Berkeley.（2023-07-19）［2023-08-20］.http：//opensees.berkeley.edu.

Mitropoulou C C，Papadrakakis M.2011.Developing fragility curves based on neural network IDA predictions［J］.Engineering Structures，33（12）：3409-3421.

Pujari N N，Mandal T K，Ghosh S，et al.2013.Optimization of IDA-based fragility curves［C］//safety，reliability，risk and life-cycle performance of structures and infrastructures，proceedings of the 11th international conference on structural safety and reliability，New York，USA：16-20.

Sainct R，F(xiàn)eau C，Martinez J M，et al.2020.Efficient methodology for seismic fragility curves estimation by active learning on Support Vector Machines［J］.Structural Safety，86：101972.

Suykens J A K，Lukas L，Vandewalle J.2000.Sparse approximation using least squares support vector machines［C］// IEEE，2000 IEEE international symposium on circuits and systems（ISCAS），2：757-760.

Suykens J A K，Vandewalle J.1999.Least squares support vector machine classifiers［J］.Neural processing letters，9（3）：293-300.

Vamvatsikos D，Cornell C A.2002.Incremental dynamic analysis［J］.earthquake engineering and structural dynamics，31（3）：491-514.

Wang W K，Luo H.2023.A dataset of reinforced concrete frame response under ground motions based on OpenSees simulations［DB/OL］.Harvard Dataverse.（2023-10-10）［2023-10-15］.https：//doi.org/10.7910/DVN/HDBJ0E.

Eigenvectors-informed Support Vector Machines for Fragility Curve Predictions of RC Frames

ZHOU Yu1，2，LUO Huan1，2

（1.Hubei Geological Disaster Prevention and Control Engineering Technology Research Center，Yichang 443002，Hubei，China）

（2.College of Civil Engineering &Architecture，China Three Gorges University，Yichang 443002，Hubei，China）

Abstract

Fragility curves establish a correlation between structural damage levels and seismic intensity，offering an intuitive depiction of the probability of structural failure.?However，the generation of these curves necessitates a substantial amount of structural nonlinear timehistory analysis results，thereby rendering the computational process inefficient.?Machine learning techniques have been proven to effectively address this issue，yet their efficacy diminishes with the increase in the scale of training data due to the computational demands of solving largescale inverse matrices during the training phase.?In response，this paper proposes a novel methodology，the Eigenvector Informationsupported Support Vector Machine（EILSSVM），which surmounts the limitations associated with these techniques.?By employing a selective subsample to construct a lowrank kernel matrix in the context of largescale datasets，the EILSSVM method requires only the inversion of smallscale，lowrank matrices，significantly enhancing computational efficiency.?To validate the accuracy and efficiency of the EILSSVM，it is benchmarked against conventional models such as the Least Squares Support Vector Machine（LSSVM），Random Forest，Neural Networks，Linear Discriminant Analysis （LDA），and Bayesian methods，using a dataset comprised of 16500 instances of damage in Reinforced Concrete（RC）frames subjected to seismic activities.?The results indicate that the EILSSVM is capable of accurately predicting the fragility curves of RC frames，with a computational efficiency improvement of up to 27 times compared to existing methodologies.

Keywords：RC frame structures；fragility curves；eigenvectors；support vector machines；machine learning

*收稿日期：2023-09-19.

基金項目：湖北省自然科學基金面上項目（2022CFB294）；國家自然科學基金青年科學項目（52208485）.

第一作者簡介：周宇（1997-），碩士研究生在讀，主要從事結構抗震與機器學習交叉研究.E-mail：891363206@qq.com.

通信作者簡介：駱歡（1988-），博士，副教授，主要從事結構抗震與機器學習交叉研究.E-mail：hluo@ctgu.edu.cn.

周宇，駱歡.2024.基于特征向量信息支持向量機的RC框架易損性曲線預測［J］.地震研究，47（3）：359-368，doi：10.20015/j.cnki.ISSN1000-0666.2024.0052.

Zhou Y，Luo H.2024.Eigenvectors-informed support vector machines for fragility curve predictions of RC frames［J］.Journal of Seismological Research，47（3）：359-368，doi：10.20015/j.cnki.ISSN1000-0666.2024.0052.