重視問題引領 構建創生課堂 發展核心素養
——以人教A版必修一“冪函數”教學設計為例*

楊 恒 (江蘇省江陰市華士高級中學 214421)

董榮森 (江蘇省懷仁中學 214196)

1 問題提出

鄭毓信教授在文[1]中提出數學教學中的三個關鍵之一是數學教學中的問題引領,并指出這一主張的原因:

第一,對于“引領”的高度重視可以被看成是由數學學習的本質所直接決定的,后者即是指學生數學水平的提高主要依賴后天的系統學習,也即主要是一個文化繼承的過程,教師在此所發揮的正是文化傳承者的作用,應當對于學生的數學學習發揮重要的引領作用．

第二,對于問題引領的強調集中地體現了“雙主體”這一基本的教學思想,即在充分發揮教師在教學過程中的主導作用的同時,我們也應很好地落實學生在學習活動中的主體地位．

第三,我們關于數學教育主要目標的分析則清楚地表明了問題引領的方向:我們應當通過設問、追問等手段促進學生更深入地思考,從而達到更大的認識深度,并能逐步學會想得更清楚、更全面、更合理、更深刻．

數學教學中應當特別重視一些方面:一是核心問題的提煉與加工;二是通過問題串的設計包括及時的調整引導學生深入地進行思考;三是努力提升學生提出問題的能力[1]．

2 教學設想

數學創生課堂是創設、生長的課堂．通過創設真實的情境,調動學生已有知識與經驗發現問題,充分激發學生啟動思維、積極思考、提出問題,生長新知識與經驗．

數學創生課堂是創新、生成的課堂．通過自主探索、合作研究等多種學習方式分析問題,關注知識的變式與生成,在不斷的創新中生成新的事物、新的概念,生成有意義的知識體系．

數學創生課堂是創造、生命的課堂．通過創造性的數學課堂教學活動解決問題,教師在課堂上“教中創”,引導學生在課堂里“創中學”,在富有創造的活動中培育富有活力的精彩生命．

本節課以問題為線索,對教材中的“冪函數”進行解構、重構和建構,通過問題引領,構建創生課堂,培養學生的創新思維和實踐能力,發展學生的數學核心素養．

3 教學流程

3.1 問題驅動:創設情境,提出問題

(1)如果張紅以1元/kg的價格購買了某種蔬菜wkg,那么她需要支付p=w元,這里p是w的函數;

(2)如果正方形的邊長為a,那么正方形的面積S=a2,這里S是a的函數;

(3)如果立方體的邊長為b,那么立方體的體積V=b3,這里V是b的函數;

問題1如果我們用x表示自變量,y表示函數值,以上函數可以分別表示成什么?

設計意圖通過對自變量和函數值的轉化,化不熟悉為熟悉,可以讓學生更專注于尋找5個函數之間的區別和聯系．

問題2觀察(1)～(5)中的函數解析式,從解析式的結構特征看,它們有什么共同特征?

追問 從函數的角度上看,底數與指數有什么共同特征?從項的角度上看,還能發現有什么共同特征?

設計意圖引導學生從解析式的結構特征去思考,發現這5個解析式的共同點．創設貼近學生生活實際的真實情境,讓學生置身情境啟動思維,從而發現問題．

3.2 主體活動:構建新知,形成概念

·冪函數的定義

設計意圖在初中學習的基礎上,不難得出冪函數的定義以及冪函數的特點．

問題4下列函數中是冪函數的有．(填序號)

設計意圖不僅要會判斷函數是不是冪函數,還要會根據條件求冪函數的解析式．設置貼近學生認知水平的數學背景,讓學生自探、自悟、自理、自明,并提出問題．通過冪函數概念的學習,提升學生的數學抽象核心素養．

3.3 合作互動:繪制圖象,研究性質

硫酸銅溶液在濃縮結晶槽內完成蒸發、冷卻結晶之后，邊攪拌邊用氣動雙隔膜泵抽取至真空帶式過濾機進料口；硫酸銅晶體在帶式過濾機上過濾、洗滌、吸干［1］，然后通過埋刮板給料運輸機輸送至流化床受料斗，進入干燥包裝工序。實驗數據表明過濾后的硫酸銅含水率在5%～10%，與原過濾器含水5%～9%基本一致，可滿足后段工序流化床干燥設備的工藝要求。

·冪函數的圖象與性質

設計意圖相對原教材,冪函數的內容和要求有較大的調整.本節課設計緊緊圍繞5個函數,從結構特征抽象出冪函數概念,從圖形特征尋找區別和共性．本環節中,在羅列5個函數性質的基礎上,教師鼓勵學生對冪函數的性質進行猜想,鍛煉學生的思維,發展學生的學科素養,讓學生感受研究一類函數的一般方法．同時,這也是一個討論點,先讓學生討論2～3分鐘,然后讓學生回答,教師點評并小結．遵循學生認知規律引導點撥,讓學生交流質疑、合作構建．通過冪函數圖象與性質的學習,提升學生的直觀想象素養．

3.4 智慧靈動:深化理解,提升素養

·定量刻畫冪函數的性質

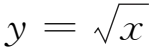
3.5 反思觸動:總結知識,提煉方法

問題9回憶本節課的內容,請你回答以下幾個問題:什么樣的函數是冪函數?你能簡單說一說本節課所學的5個冪函數的性質嗎?在本節課中,你經歷了怎樣的學習過程?涉及哪些數學思想方法?還有哪些疑惑或問題?

設計意圖通過梳理本節課的內容,讓學生更加明確冪函數的定義和常見的5個冪函數的性質．貼近學生個性、素養差異設計問題,歸納總結反思過程,生成問題．

4 教學反思

章建躍博士指出:把“冪函數”安排在第三章《函數的概念與性質》第3.3節,主要是借助對這一類函數的研究,使學生理解研究一類函數的內容、基本思路和方法,圍繞函數概念這個核心,從相互聯系的觀點出發,利用函數與數、代數式、方程、不等式等之間的聯系,通過類比、歸納和概括,引導學生從不同角度理解函數概念[2]．

4.1 問題引領,落實核心概念教學

本節課的核心問題是:什么是冪函數(定義、表示)?冪函數有什么特點(圖象與性質)?通過第一組“問題串”(問題1～4),對第一個核心問題進行提煉與加工．通過第二組“問題串”(問題5～8),對第二個核心問題進行提煉與加工．同時,及時地調整設問,引導學生進行深入思考,并努力提升學生提出問題的能力．

4.2 創設問題,促進學生思維生長

4.3 自主構建,關注知識生成創新

4.4 合作交流,創造彰顯生命活力

“創生”一詞出自魯迅先生的《集外集拾遺》,意思是創造產生,生而成長．這便也是“數學創生課堂”的初衷與情懷!