學好“一次函數”的必備攻略

領 "銜 "人：姜鴻雁（江蘇省特級教師）

組稿團隊：江蘇省無錫市初中數學名師工作室

同學們，你知道嗎，函數被德國著名數學家克萊茵稱為數學的“靈魂”，可見它的地位和價值至關重要。學完“一次函數”之后，有的同學感到些許迷糊，甚至覺得有點難。那我們就一起來看看學好一次函數的幾條必備“攻略”吧。

攻略一：明晰概念，經歷數學抽象，認識數學模型

函數研究的是一個變化過程中兩個變量x、y之間的關系，當變量x取一個值，變量y有唯一值與它對應。函數是從“常量數學”到“變量數學”的跨越，必然進入另一番天地。函數是一個“龐大的家族”，我們從最基本、最簡單的一次函數開始學習，它的定義是：形如y=kx+b（k、b是常數，k≠0），y是x的一次函數。它就在我們的生活中，比如：

（1）一輛汽車的油箱中現有汽油5L，加油槍平均加油量為6L/min，那么油箱中的油量y（L）與時間x（min）之間的函數表達式為y=6x+5；

（2）某水庫的水位在5h內持續上漲，初始水位高度為6m，水位以每小時0.3m的速度上升，則該水庫的水位高度y（m）與時間x（h）之間的函數表達式為y=0.3x+6；

（3）某登山隊大本營所在地的氣溫為30℃，海拔每升高1km，氣溫下降6℃，登山隊員所在位置的氣溫y（℃）與海拔x（km）之間的函數表達式為y=-6x+30。

透過現象看本質，這些實際問題反映的等量關系都是：新值=均勻變化部分+初始值，因此可以抽象出y=kx+b（k≠0）這個數學模型來描述共性。

攻略二：研究圖像，體會數形結合，培養幾何直觀

一次函數的圖像是一條直線，以此表達“均勻變化”的特質，其圖像位置由k和b決定。我們可以用“控制變量法”來理解。

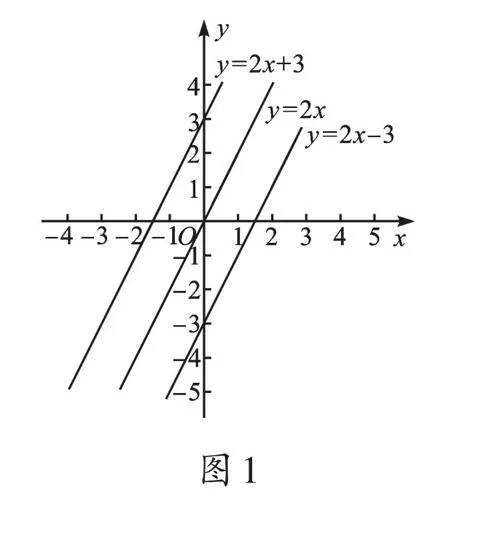
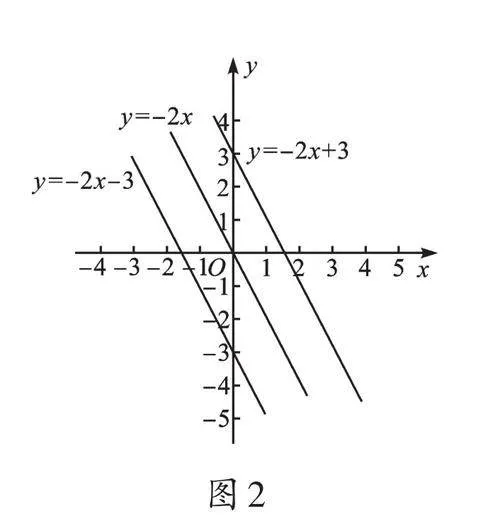
設k=2（如圖1），隨著b的變化，圖像的位置發生變化，但相互平行；當k=-2時（如圖2），也是如此。對比圖1、圖2可知，k值影響圖像走勢：當k＞0時，y隨x的增大而增大（上升），必過第一、三象限；當k＜0時，y隨x的增大而減小（下降），必過第二、四象限。

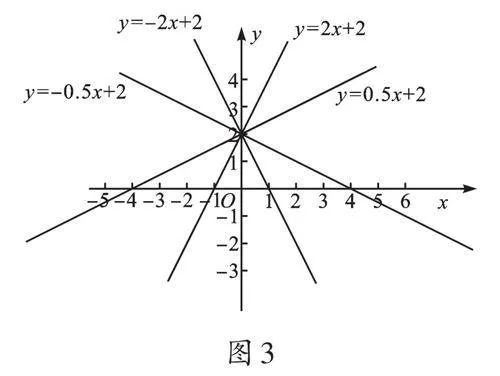
再設b=2（如圖3），隨著k的變化，圖像與y軸的公共點始終為（0，2）。

可見，k、b的取值與圖像的位置建立了聯系。例如，若一次函數y=kx+k+1的圖像不經過第三象限，求k的取值范圍。這里要注意，“不經過第三象限”指經過第一、二、四象限或經過第二、四象限和原點。此類問題都只需畫出草圖，以形助數，故此題答案為-1≤k＜0。

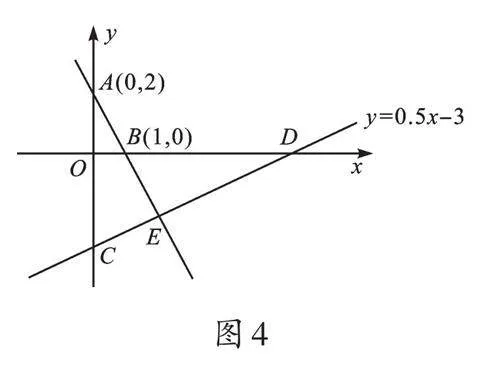
借助數形結合，我們還可以進一步研究如下問題。如圖4，觀察圖像的信息，可求直線AB的函數表達式和點C、D坐標，聯立兩個表達式還可以求出點E坐標；利用圖像法能求出不等式-2x+2＞0.5x-3的解集；還可求出△BED的面積……

通過研究一次函數圖像，我們可以深入理解它的性質，深度剖析它與方程、不等式之間的關系，培養幾何直觀的能力。

攻略三：回歸生活，體驗建模過程，實現問題解決

函數源自生活，回歸生活。在實際生活中，一次函數一直發揮著它的應用價值。

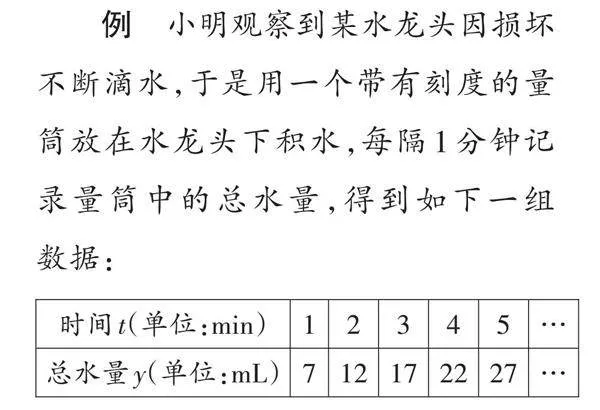
例 小明觀察到某水龍頭因損壞不斷滴水，于是用一個帶有刻度的量筒放在水龍頭下積水，每隔1分鐘記錄量筒中的總水量，得到如下一組數據：

（1）開始計時時，量筒中有水嗎？

（2）20分鐘時，量筒中的水量是多少mL？

（3）一個人一天大約飲用1500mL水，估算這個水龍頭一個月（按30天計）的漏水量可供一人飲用多少天。

觀察表格發現，前后一分鐘都相差5毫升水，具有“均勻變化”特質，故建立一次函數模型：y=kt+b（也可以把一組組值作為點的坐標，在平面直角坐標系中描出，觀察函數圖像），用待定系數法求出表達式y=5t+2；令t=0，y=2（mL）；令t=20，y=102（mL）；1個月的總滴水量：30×24×60×5=216000（mL），再得天數：216000÷1500=144（天）。真是不算不知道，一點一滴皆重要！

同學們，以上“攻略”沿著“概念、圖像與性質、實際應用”的路徑展開，這也是學習函數的一般路徑，為日后學習其他類型的函數積累經驗。一次函數僅僅打開了函數的大門，里面有非常廣闊的天地任我們馳騁，讓我們一起慢慢細品這一“數學之魂”吧！

（作者單位：江蘇省宜興外國語學校）