平面直角坐標(biāo)系的前世今生
平面直角坐標(biāo)系是初中階段的一個重要工具,它既聯(lián)通了“數(shù)”與“形”,也為后面學(xué)習(xí)函數(shù)奠定了基礎(chǔ)。這個工具是怎么產(chǎn)生的呢?讓我們一起坐上時光機(jī)去探尋吧!
早在我國西晉時期,裴秀主編的《禹貢地域圖》中就提出了繪制地圖的思想,包括比例尺、方向和距離。可見我國古人已經(jīng)學(xué)會用量來定位。
用數(shù)來表示量和用簡潔的有序數(shù)對來表示位置的想法最早出現(xiàn)在古希臘和阿拉伯。阿波羅尼奧斯等數(shù)學(xué)家認(rèn)為平面內(nèi)的點可以用有序數(shù)對進(jìn)行一一對應(yīng);法國數(shù)學(xué)家奧雷姆研究運動問題時用水平直線表示時間,直線上的點代表時刻,用垂直于此點的線段長度代表速度。這里直線相當(dāng)于橫軸,時間和速度的實質(zhì)就是橫縱坐標(biāo)。
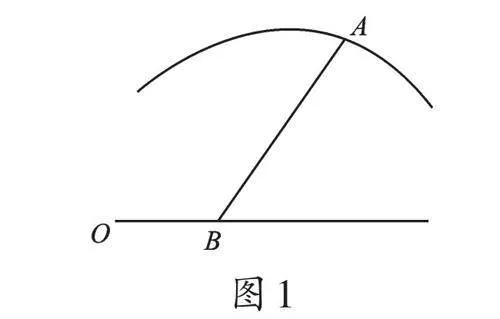
直到法國數(shù)學(xué)家笛卡爾和費馬登場,他們推動了解析幾何的發(fā)展。笛卡爾在研究帕波斯問題時以一條直線作為基線,又選擇一條線段,這條線段從基線出發(fā),與基線形成了定角,這就是歷史上第一個坐標(biāo)系。費馬任取曲線上一點,連接基線上一點,此時用點O到點B、點A到點B的距離表示點A的位置(如圖1所示)。
英國數(shù)學(xué)家沃利斯在笛卡爾的基礎(chǔ)上進(jìn)行改進(jìn),首次引入負(fù)的橫縱坐標(biāo)。后來,隨著牛頓、伯努利、萊布尼茨等數(shù)學(xué)家的進(jìn)一步完善,平面直角坐標(biāo)系等概念被提出,并將坐標(biāo)系推廣至三維空間乃至超級空間。
平面直角坐標(biāo)系的建立是數(shù)學(xué)發(fā)展過程中的一次轉(zhuǎn)折,讓代數(shù)和幾何不再是兩條永不相交的平行線,構(gòu)建了點與有序數(shù)對的對應(yīng)關(guān)系。這為解決生活問題提供了方法,比如電影院座位分布、GPS定位系統(tǒng)、監(jiān)測臺風(fēng)實時路徑等。隨著我們學(xué)習(xí)的深入,坐標(biāo)系的應(yīng)用也會更加廣泛。
(作者單位:江蘇省南京市鐘英中學(xué))

