由坐標確定位置的一點思考

學習了平面直角坐標系這一章內容后，我覺得平面直角坐標系中圖形位置的變化與點的坐標變化之間的關系很有趣，但又有些困惑。于是，我對平面直角坐標系中兩點的位置變化進行了一些探究和思考。

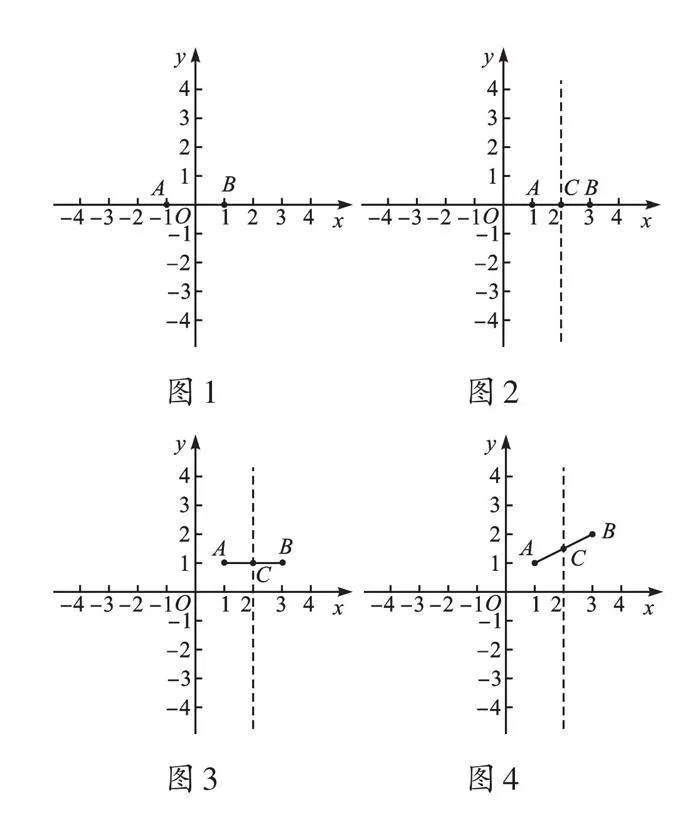
如圖1，點A（-1，0）、B（1，0）關于y軸對稱，線段AB被y軸垂直平分，那么點O就是線段AB的中點。現將線段AB沿x軸向右平移2個單位（如圖2），則平移后的A、B兩點的坐標分別為A（1，0）、B（3，0），對稱軸也隨之向右平移2個單位，線段AB的中點為C（2，0）。繼續將線段AB沿y軸向上平移1個單位（如圖3），平移后的A、B兩點的坐標分別為A（1，1）、B（3，1），此時對稱軸沒有變化，線段AB的中點為C（2，1）。此時，我發現一個有趣的現象，三個圖形中線段AB中點的坐標和A、B兩點的坐標有共同的規律：線段AB中點的橫坐標是A、B橫坐標之和的一半，縱坐標和A、B縱坐標相等。

接下來我改變了點B的位置，在圖3的基礎上將點B向上平移一個單位，此時點B的坐標為（3，2），點A的位置不變（如圖4）。這時候我發現，線段AB的中點C仍然在圖3中線段AB的對稱軸上，所以橫坐標沒有變化，仍是點A、B橫坐標之和的一半；但縱坐標發生了變化，從圖中的位置看，大于點A的縱坐標，且小于點B的縱坐標。如何求出點C的縱坐標呢？我陷入了沉思。

在認真閱讀了教材中關于點的坐標的概念后，我了解到要求點C的縱坐標，就是要求出點C到x軸的距離。但苦思冥想后，我還是不知道該如何求解，于是請教了老師。老師提示我要抓住“點C是AB中點”這一關鍵條件，巧用三角形全等的知識解決這個問題。

在老師的指導下，我順利構造了如圖5的一對全等三角形：△ACE與△BCD，其中∠AEC=∠BDC=90°。于是就得到了CE=CD=[12]，進而求得CH=CE+EH=[12]+1=[32]，即點C到x軸的距離為[32]，最后得到點C的坐標為（2，[32]）。這時我發現點C的縱坐標也是點A、B縱坐標之和的一半。

于是我作了如下猜想：對于平面直角坐標系中任意兩點A（x1，y1）、B（x2，y2），當C（x，y）是線段AB中點時，則有x=[x1+x22]，y=[y1+y22]。我把自己的猜想和老師進行了交流，老師肯定了我的猜想，并鼓勵我和同學們一起作更一般化的探索。在和同學們一起討論交流后，我們進行了一般化的推理，推理過程如下：

如圖6，過點C作x軸的垂線MN，分別過點A、B作直線MN的垂線，垂足分別為點E、D，則∠AEC=∠BDC=90°。

又∵∠ACE=∠BCD，AC=BC，

所以△ACE≌△BCD。

所以AE=BD，CE=CD，

即x-x1=x2-x，y-y1=y2-y。

所以x=[x1+x22]，y=[y1+y22]。

教師點評：

小作者在探究平面直角坐標系中點的位置變化與其坐標數量變化之間的關系時，發現并自主探索得到了中點坐標公式，巧用本學期剛學過的三角形全等的知識給出了推理和論證，在探索過程中加深了對數形結合這一重要數學思想方法的理解。這種基于對數學的興趣和好奇而進行的探索之旅，體現了小作者樂學善學，善于發現問題、解決問題的良好思維品質。

（指導教師：方秀林）