考慮機場、航空公司與空管需求的機場群離場航班時刻優化

張兆寧, 劉澤鏵

(中國民航大學空中交通管理學院, 天津 300300)

隨著需求的提高,中國航班量不斷增加。2019年,中國運輸航線完成運行架次986.8 萬架次,相較于2015年的729.4 萬架次提升約35.3%。隨著航空運輸的逐步恢復,流量將會不斷增加。

機場群是指在一定區域范圍內,以一個或多個大型機場為核心,各機場與區域間其他城市通過基于航空需求的地面運輸聯系而形成的空間集群。機場群不僅是區域內多個機場的簡單集合,更是差異化與協同發展為主要特征的多機場體系。目前,國內已初步形成京津冀、長三角、珠三角、成渝四大機場群。

隨著航班量的增加以及機場群間各機場航班起落的相互影響,機場群內樞紐機場高峰時段時隙資源十分緊張,如遇到天氣等突發狀況,會導致樞紐機場航班出現大量延誤。航班的延誤現象主要是由于航班時刻設置不合理,因此,需要對機場群航班時刻進行優化,以防止大量延誤現象的發生。

在對于航班時刻優化方面的研究,國內外學者有了不少研究成果。

國外學者Benlic[1]設計了啟發式算法以分配機場航班時刻,并通過反復迭代得到了優化后的航班時刻分配;Pellegrini 等[2]提出機場航班時刻分配同步優化的模型,可以對歐洲內機場的航班時刻進行分配。

國內學者盧婷婷等[3]以對目的地機場產生的影響與航班運行延誤作為目標建立優化模型,以武漢天河機場作為案例進行優化;左杰俊等[4]針對航班實時調度問題,以航班調整量與航班運行延誤為目標建立優化模型,并以成都雙流國際機場為例進行分析;楊琳等[5]以航班總延誤時間最短為目標,以機場容量、區域管制扇區容量、航班時刻調整量為約束條件,建立優化模型,并以上海浦東國際機場為例進行優化;柯雨辰等[6]以跑道、機位以及走廊口構成的系統為對象,以最小化航班時刻偏移化為目標函數建立模型,利用MATLAB內部的線性整數規劃工具箱intlinprog進行求解,以冬春浦東機場為例進行優化;陳彬等[7]為解決航班時刻優化時不同目標之間相互影響的問題,提出了基于零和博弈的航班時刻優化模型,將航班總延誤和總調整量轉化為一個整體,并使用螢火蟲算法進行求解;劉田野等[8]提出從飛機輪擋時間的相關事件具有隨機性的角度對航班時刻進行優化,首次使用泰爾指數作為公平性目標函數,使用粒子群算法進行求解,以杭州蕭山國際機場為例進行分析。

隨著研究的深入,近些年來許多學者開始轉向對多機場與機場群的航班時刻優化進行研究。

國外學者Clarke等[9]建立了機場群各機場之間關系的方式,進一步確認了機場群內各機場之間的影響因素,認為航路當中的間隔以及機場的時間調度是緩解終端區延誤狀況的最主要因素;Rahmalia等[10]將時刻和機組人員的成本進行了匹配,運用了蝙蝠算法對航班時刻進行了優化;Flores[11]通過研究機場群內樞紐機場的相關問題,通過構建與機型有關的相關模型發現樞紐機場航班擁擠主要是因為使用過多航班采用較小機型;Yoo等[12]通過對紐約機場群的兩種運行狀況進行了仿真分析,證實了紐約機場群的一體化需求管理所帶來的一定效益;Zografos等[13]以航班時刻不可接受的調整量以及總調整量作為優化目標,建立雙目標規劃模型,使結果更容易被航空公司所接受;Liu等[14]以地面周轉時間、航班連接性、總延誤時間作為目標,將遺傳算法與多目標優化方法結合進行求解。

國內學者陳梵驛等[15]以機場群總體效益最大化為優化目標,并將決策樹C4.5算法應用于優化問題之中。王倩[16]列舉了世界級機場群的概念與相關定義,針對機場群的大面積延誤問題,以航班總調整量為目標函數建立了機場群航班時刻優化及動態排隊雙層規劃模型,并使用改良的粒子群算法對珠三角機場群進行驗證;劉佳等[17]以總費用最小為目標,建立了優化模型,并設計了啟發式算法對航班時刻進行優化;王興隆等[18]建立了機場群離港航班時刻穩定性評估指標對航班時刻進行穩定性評估,以總延誤成本為目標建立優化模型,使用粒子群算法對京津冀機場群進行了評估;李昂等[19]以系統整體準點率最大化為優化目標,采用迭代尋優算法,最終通過對比發現優化后航班時刻沖突水平與延誤水平均有一定程度降低;朱承元等[20]為降低珠三角地區的航班延誤,提出以延誤分層模型為優化目標進行空域機場仿真模型進行建模,同時和有約束限制的并行擾動隨機近似優化算法相結合,對珠三角機場群的航班時刻進行仿真研究優化;王倩等[21]在滿足延誤水平基礎上,基于航空公司公平性設計了航班時刻表的優化模型,并使用布谷鳥搜索算法進行航班時刻表優化;王興隆等[22]以延誤總成本與延誤總時間為目標,建立終端區多機場的協同放行模型,采用改進的多目標粒子群算法對所見模型進行求解;翟文鵬等[23]提出程序交叉容量約束對航班時刻進行優化,以航班時刻總調整量以及各航空公司調整量作為目標,并運用模擬退火算法進行求解;林雍雅[24]從戰略和戰術層面對機場群航班時刻進行研究,以航班時刻調整量及調整次數為目標函數建立戰略層航班時刻優化模型,以延誤時間成本為目標函數建立戰術層航班時刻優化模型;薛依晨[25]在考慮航線穩定性的基礎上,以總延誤成本為目標,建立了機場群航班時刻優化模型;陳彬[26]以航班總延誤及調整量、疏解航班貼合度、機場收益作為目標函數建立多機場航班時刻模型,對多機場間的博弈進行仿真分析,考慮機場準點率、航空公司市場占用率、機場功能定位作為目標函數;水笑雨等[27]從考慮機場公平性的角度入手,以航班時刻偏移量和機場群中機場公平性為目標,建立機場群航班時刻優化模型,以大灣區機場群為例進行分析;林思奇[28]對區域多機場系統航班時刻優化展開研究,從航空運輸企業和旅客角度出發,對航班時刻展開研究;向征等[29]針對多機場終端區空域資源緊張的問題,以總調整時間最小化為目標提出基于管制移交間隔優化的離港航班時刻模型,采用遺傳算法進行求解,使用北京終端區下轄的北京大興機場、北京首都機場與天津濱海機場為例進行實例認證。

綜上文獻,可以看出學者對于航班時刻優化的規劃模型目標大多數集中于延誤時間、延誤成本、航班調整量、系統準點率等方面,規劃模型求解尋優方法多采用遺傳算法、粒子群算法、蟻群算法、模擬退火算法等。

由于機場群內航班時刻的設定主要由機場、航空公司與空管3方所決定。此前對于機場群航班時刻的研究多數集中于機場、航空公司、空管的其中一個或兩個角度,考慮角度不夠全面,并沒有從機場、航空公司、空管3個方面同時進行考慮。現以機場、航空公司與空管3個方面為主要方向,以航班總延誤時間、航空公司總延誤方差、航班總調整量為目標,建立機場群航班時刻的優化模型,并使用權重線性遞減的粒子群算法對模式進行求解。為驗證模型的有效性,以京津冀機場群為例,將建立的模型運用權重線性遞減的粒子群算法進行運算,對機場群航班時刻進行優化,以促進機場、航司、空管三方之間的平衡。

1 模型建立

機場群內航班時刻的設定主要由機場、航空公司與空管三方所決定,因此考慮機場、航空公司、空管三方之間的平衡來建立模型。

從機場、航空公司、空管3個角度設立目標函數。從機場角度出發,實現航班總延誤最小比較重要,設立航班總延誤時間為優化目標;對于航空公司,各航空公司之間的公平性較為重要,設立航班時刻調整總方差為優化目標;對于空管,需要降低管制員的工作負荷,設立管制員調整航班總次數作為目標。

根據機場群實際運行情況,考慮主要的約束條件,給出模型約束條件如下。

由于每個航班僅可選擇一個時段離場,設立航班唯一性約束;參照機場群內設立航班時刻的主要制約因素,設立機場及機場群容量作為容量約束條件;航班無法提前起飛,僅能按時或延誤起飛,且航班延誤時間不得超過最大延誤時間,設定航班時刻調整量約束。

1.1 問題描述

假設如下條件。

(1)機場群內各機場起飛航班與降落航班不相互影響。

(2)機場航班時刻以5 min作為最小的時間單位。

(3)調整前后航班及航班總量與出發機場不變,僅調整離場時刻。

1.2 變量設置

(2)xs:航空公司s離港航班總數。

(3)tf:航班f的預計時刻。

(4)tfs:航班f的實際時刻。

(5)tmax:最大延誤時間。

(6)mi:i機場單位時間的最大容量。

(7)m:機場群單位時間的最大容量。

(8)Cf:航班總調整次數。

(9)X:離場航班集合。

(10)F:航班集合。

(11)Fs:航空公司s的航班集合。

(12)A:機場群內部機場集合。

(13)S:航空公司集合。

(14)T:進港與離港航班時刻集合。

1.3 目標函數

(1)機場角度。設立總延誤時間最小作為目標函數。

(1)

(2)航空公司角度。設立各航空公司航班時刻調整總方差最小化作為目標函數。

(2)

(3)空管角度。設立管制員調整航班次數的最小化作為目標函數。

minZ3=Cf

(3)

1.4 約束條件

(1)航班唯一性約束。

(4)

(2)機場容量約束。

(5)

(3)機場群容量約束。

(6)

(4)航班時刻調整量約束。

0≤tfs-tf≤tmax

(7)

2 模型求解算法設計

在對機場群時刻優化過程中,通常使用蟻群算法、遺傳算法、粒子群算法等算法對優化模型進行求解。粒子群算法具有群體智能、內在并行性、迭代格式簡單等優點,同時可以快速收斂到最優解的所在區域。

由于機場群每日航班架次多,涉及數據量較大,對航班時刻進行尋優具有一定的難度。粒子群算法較為簡單,同時收斂快速,比較適合用于求解所研究的優化問題。因此選用粒子群優化算法作為求解優化問題的算法。

傳統的粒子群算法存在早熟性,容易陷入局部最優的狀況,進而導致尋優結果的誤差較大。考慮到粒子群算法的早熟性,進一步對算法進行改進,采用權重線性遞減的粒子群優化算法對模型進行求解。

由于需要通過加權求和將多目標函數轉化為單目標函數進行求解,在設計適應度函數時使用變異系數法對目標函數進行去量綱化。

2.1 權重線性遞減的粒子群優化算法

粒子群算法(particle swarm optimization,PSO)是一種通過模仿鳥類捕食運動而誕生的算法。其將鳥類的飛行空間比作搜索的目標空間,將每只鳥比作在空間運動的無質量體積的粒子,以代表當前問題的一個解。每個粒子分別包含位置與速度兩個因素,其中位置代表粒子當前所處的方位,速度代表粒子移動的距離與方向。通過粒子不斷更新自身的最優位置,找到穩定的最優解。

傳統的粒子群算法在計算函數的過程中常常出現早熟現象,容易陷入局部最優,導致系統收斂性較弱,因此需要對粒子群算法進行改進。由于較大的權重利于粒子跳出局部最小點,利于全局搜索,而較小的權重則利于對當前的搜索區域進行精確的搜索。因此針對PSO算法前期易早熟、后期易波動的特點,采用權重線性遞減的PSO算法。該算法進一步提高了迭代尋優的能力。

根據迭代次數的變化,慣性權重不斷由最大值ωmax減少至ωmin,慣性權重的變化公式為

(8)

式(8)中:M為當前迭代次數;Mmax為最大迭代次數。

2.2 算法參數設計

根據涉及的航班時刻優化問題,設計算法所涉及的相關參數。

2.2.1 粒子設計

針對航空時刻優化問題,定義每個粒子的位置表示代表所排序的一組時刻集合,每個粒子的維度等于航班數目。其中每個粒子中的每個向量包含離場時間tn、機場群內的起飛機場an、所屬航司sn。

2.2.2 速度更新

粒子群的速度更新公式為

(9)

式(9)中:rand為0～1的隨機數;gbest為當前粒子的個體最優位置,即當前最佳時刻安排;zbest為當前種群的全局最優位置;c1、c2為學習因子。

2.2.3 適應度函數

在每次迭代過程中,需要對此次迭代的狀況進行評價,適應度函數便是評價此次迭代是否最優的函數。

采用加權求和法將多目標函數轉化成單目標函數,設定適應度函數。經過分析,最終適應度函數設計為

fitness=α1Z1+α2Z2+α3Z3+Ma

(10)

模型綜合考慮3個方向,3個目標函數之間并無優劣之分,各指標重要性相等,但由于各目標函數度量指標不同,需要對各函數進行去量綱化,使得不同單位之間的目標函數可以進行加權求和。根據歷史航班數據,使用變異系數法進行標準化處理。

變異系數法是根據統計學方法計算得出系統指標變化程度的方法,是一種客觀賦權的方法。變異系數法作為適應度函數權重參數αj的參考,具體步驟如下。

步驟1計算各目標函數均值和標準差。

(11)

(12)

步驟2計算變異系數。

(13)

步驟3計算權重。

(14)

式中:mj為目標j樣本數據的均值;sj為目標j樣本數據的標準差;vj為變異系數。

2.3 算法步驟

運用權重線性遞減的粒子群優化算法求解機場群離場航班時刻優化模型的具體步驟如下。

步驟1讀取初始航班時刻數據,作為初始解,并根據設置粒子群數量生成其余解。其中每組航班時刻代表一個粒子的位置。

步驟2根據初始解計算初始適應度函數,將其作為當前最優適應度函數。

步驟3計算權重(隨著迭代次數線性遞減),生成速度,并進行速度及位置更新,計算適應度函數。

步驟4判斷當前粒子位置是否符合約束條件,若符合,則進入下一步。

步驟5若當前適應度函數優于最優適應度函數,則更新最優位置及最優適應度函數。若迭代未完成,返回步驟3繼續迭代。

步驟6迭代次數完成,輸出最優適應度函數以及最優時刻。

該算法流程圖如圖1所示。

圖1 算法流程圖Fig.1 Flow chart of algorithm

3 實例分析

京津冀機場群包含北京首都國際機場、北京大興國際機場、天津濱海國際機場、石家莊正定國際機場共4個機場,是中國目前四大機場群之一,2019年總起降航班874 216 架次,日均起降航班2395 架次。以京津冀機場群內部4座機場作為實例,運用機場群離港航班時刻優化模型對機場群內各機場航班時刻進行優化。

3.1 樣本選取

3.1.1 信息獲取

獲取2023年4月11日的京津冀機場群4 個機場07:00—14:00時段的共561個離場航班數據,其中北京首都國際機場離場航班共224個,北京大興國際機場離場航班共209個,天津濱海國際機場離場航班共86個,石家莊正定國際機場離場航班共42個。獲取數據包含航班號、航班預計離場時刻、航班實際離場時刻、執行航司、起飛機場。

獲取原始航班數據(部分)如表1所示。

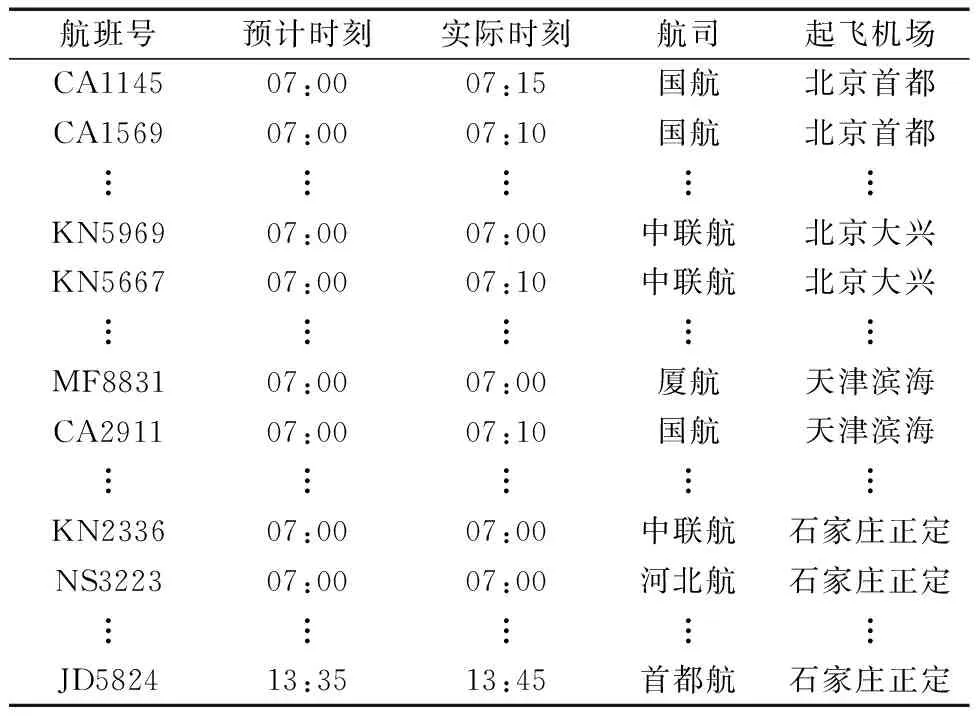
表1 2023年4月11日京津冀機場群離場航班數據Table 1 Data of departure flights of the Beijing-Tianjin-Hebei airport group on April 11, 2023

3.1.2 容量設置

參考民航局所公布的國內機場高峰小時容量數據,定義各機場最大容量如表2所示。

表2 機場容量設置表Table 2 Airport capacity setting table

3.1.3 算法參數設置

(1)權重。對于權重線性遞減的粒子群算法,早期設置較大的權重可以利于全局搜索,后期設置較小的權重利于局部搜索,加快收斂。設置最大權重ωmax= 0.9,最小權重ωmin= 0.4。

(2)種群大小。若種群大小設置太大,則收斂速度較慢;若種群大小設置太小,則容易陷入局部最優。根據多次實驗,設置種群大小N=100。

(3)迭代次數。若迭代次數設置過大,則優化結果體現不明顯,若迭代次數設置過小,則數據不夠精確,無法確定是否已經收斂到最優。根據多次實驗,發現適應度函數多數在200～400 次收斂至最優,設置最大迭代次數M=500。

(4)適應度函數權重參數。選取天津濱海國際機場2023年3月離場航班數據作為參考。通過變異系數法對目標函數進行標準化處理。最終得到適應度函數的權重參數αj如表3所示。

表3 函數權重參數設置Table 3 Object function weight

3.2 結果分析

通過使用MATLAB軟件對模型進行仿真,最終得到適應度曲線變化如圖2所示。

圖2 仿真收斂情況Fig.2 Simulation convergence situation

從圖2中可以看出,隨著迭代次數的增加,適應度函數值逐漸減少,在迭代約160 次左右趨于穩定,達到最優,由原來的739.607 減少至 377.985,有了較大幅度的變化。

各目標函數隨著迭代次數的變化分別如圖3、圖4、圖5所示。

圖3 總延誤時間收斂情況Fig.3 Convergence of total delay time

圖4 航司方差收斂情況Fig.4 Convergence of airline variance

圖5 管制員調整量收斂情況Fig.5 Convergence of controllers adjusting amount

分別從總延誤時間、航司方差及管制員調整量3個目標函數來看,各目標函數均在160次左右收斂至最小值,達到最優。時段內航班的總延誤時間由最初的77 580 min減少至46 260 min;各航司的航班調整方差由最初的447.076減少至63.141;管制員的總調整量由467次減少至253次。3個目標均得到了較好的優化。

優化前后航班時刻分布如圖6和圖7所示,部分離場航班優化前后時刻表4所示。

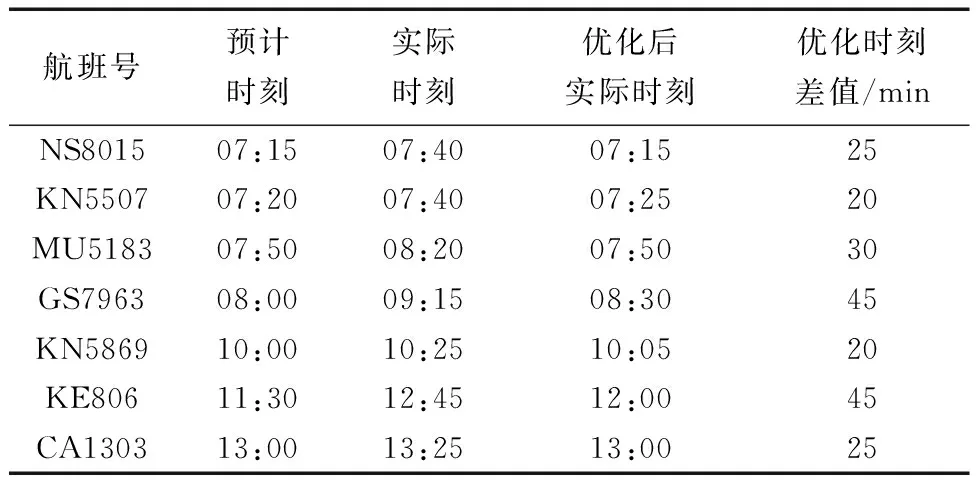
表4 部分離場航班優化前后時刻Table 4 Part of departure flight time before and after optimization

圖7 優化后航班時間分布Fig.7 Optimized flight time distribution

圖6 優化前航班時間分布Fig.6 Optimization of flight schedule distribution before optimization

從原始航班時刻分布與優化后航班時刻分布對比來看,原始航班時刻分布波動較大,出現個別較大高峰值,各機場分布不均衡,由于機場群內各機場高峰期均為08:00左右,容易互相沖突導致航班延誤;優化后航班時刻更加平穩,單時段最大航班量有了一定的減少,尤其是航班量較大的北京首都國際機場和北京大興國際機場,各機場整體時刻分布相較于原始航班時刻分布更加均衡。從離場航班優化前后時刻可以看出,優化對于延誤時間較長的航班有著較好的效果,對于延誤時間較短的航班也有一定程度的優化,整體優化效果明顯。

4 結論

研究了機場群的航班時刻優化問題,創新地從機場、航空公司、空管3個角度出發進行考慮,提出以機場群總延誤時間、航空公司航班時刻調整總方差、管制員總調整量為目標的機場群航班時刻優化模型。選用了慣性權重遞減的粒子群優化算法對該模型進行尋優。以京津冀機場群的4座機場作為研究對象,通過MATLAB進行模型仿真,最終通過結果表明以上3種目標均得到一定程度的優化,航班時刻分布更加均勻,管制員工作負荷降低,機場、航空公司、空管三方之間的公平性得到了提升,證明了該模型的有效性,為機場群航班時刻優化領域的研究做出了貢獻。