借助度量結(jié)構(gòu) 促進遷移式學習
——“長方體和正方體的體積”單元教學設計與實踐

北京第一師范學校附屬小學 高向輝

北京市房山區(qū)教師進修學校 張 艷

北京第一師范學校附屬小學 刁善玉思佳

指導教師：北京教育科學研究院 劉延革

新課標在課程實施中提出，要注重教學內(nèi)容結(jié)構(gòu)化。把握知識間的關(guān)聯(lián)，建構(gòu)有支撐意義的知識結(jié)構(gòu)，能幫助學生學會用整體的、聯(lián)系的、發(fā)展的眼光看問題，促進遷移式學習，更好發(fā)展數(shù)學核心素養(yǎng)。

體積是小學階段最后一次幾何度量的學習。在此之前，學生已經(jīng)學習了長度、面積、角度，經(jīng)歷了共性化的認識路徑，積累了學習經(jīng)驗，初步形成幾何度量的認知結(jié)構(gòu)。因此，可以引導學生借助已有的度量學習經(jīng)驗與認知結(jié)構(gòu)，運用遷移學習體積，并在學習過程中進一步豐富完善度量的認知結(jié)構(gòu)，以促進學生形成更廣泛的遷移，培養(yǎng)核心素養(yǎng)。下面具體闡述單元整體設計和實施的思考。

一、單元的學習主題及具體觀念

（一）聚焦課標變化，明確度量學習的方向

“長方體和正方體的體積”屬于圖形與幾何領域中“圖形的認識與測量”這一主題。新課標將圖形認識與測量合并為一個主題，更關(guān)注二者之間的聯(lián)系。對于立體圖形的學習，新課標要求教師引導學生通過對立體圖形的測量，從度量的角度認識立體圖形的特征，進一步發(fā)展空間觀念。有關(guān)體積的學習內(nèi)容，新課標提出：要通過實例了解體積的意義，知道體積的度量單位，能進行單位之間的換算，體驗不規(guī)則物體體積的測量方法，探索并掌握長方體、正方體的體積計算公式，能用這些公式解決簡單的實際問題。從中可以看出，新課標是從認識“度量屬性”、確定“度量單位”、探索“度量方法”、解決“實際問題”的角度明確了學習內(nèi)容，提出了具體要求，同時這也是學生認識體積要經(jīng)歷的學習過程。這樣的學習過程與長度、面積、角度的學習具有一致性，素養(yǎng)表現(xiàn)是量感和推理意識。

（二）分析教材設計，梳理度量學習的結(jié)構(gòu)

“長方體和正方體”這個單元是學生第一次深入研究立體圖形，是從二維平面圖形到三維立體圖形的一次跨越。學生通過展開與折疊、視圖與還原、切割與堆積多角度進行二維與三維的轉(zhuǎn)化，認識了長方體、正方體的特征。但如何從量化的角度認識三維空間呢？這就需要引入新的度量屬性—體積。

對比人教版、北京版和北師大版小學數(shù)學教材，三個版本教材在編排時都引導學生經(jīng)歷“認識度量屬性體積—確定體積單位—單位累加度量體積—探索體積與圖形要素關(guān)系獲得公式—選擇合適方法解決生活問題”的過程，這樣的研究過程與學習長度、面積、角度相同，體現(xiàn)了認知結(jié)構(gòu)的一致性。

北京版和北師大版小學數(shù)學教材在編排中更突顯溝通長度、面積、體積之間的聯(lián)系，引導學生借助已有經(jīng)驗和認知結(jié)構(gòu)，運用遷移學習體積度量，豐富對度量內(nèi)涵的認識，在聯(lián)系與對比中進一步完善度量的認知結(jié)構(gòu)。這樣的學習過程符合學生的認知，也體現(xiàn)了知識的進階。

綜上分析發(fā)現(xiàn)，體積與長度、面積、角度都在圍繞度量的本質(zhì)展開教學，它們之間呈現(xiàn)出來的知識結(jié)構(gòu)和思維方法具有一致性。所以，教學時可以運用類比遷移，引導學生借助已有的學習經(jīng)驗和方法自主探究，使學生體會到度量的認知結(jié)構(gòu)是可遷移的，能應用到新的度量學習中。在這個過程中，發(fā)展量感、推理意識、空間觀念，以及解決實際問題能力和創(chuàng)新意識。因此，北京研究團隊確定了本單元的學習主題和具體概念。

（三）單元具體概念及學習主題

學習主題：借助結(jié)構(gòu)，促進遷移。單元具體概念如下：

具體概念一：體積刻畫物體所占空間的大小，度量的基本方法是體積單位的累加。通過尋找長方體、正體積與要素之間的關(guān)系，獲得體積公式。

具體概念二：解決體積問題選取的度量方法和度量單位源于實際生活的需要。

具體概念三：在上述過程中，發(fā)展學生量感、推理意識、空間觀念，以及解決問題的能力及創(chuàng)新意識。

以上的單元具體概念明確了度量對象、度量過程和素養(yǎng)目標。本單元要在單元具體概念引領下，基于學生已有的認知結(jié)構(gòu)來展開教學。

二、學情分析

所謂認知結(jié)構(gòu)，就是學生頭腦中的知識結(jié)構(gòu)。學生掌握新知識的過程，即是他們逐步完善認知結(jié)構(gòu)的過程。根據(jù)教材中度量領域的學習路徑分析，得知學生在中、低年級學習長度、面積、角度的時候，早已進行了結(jié)構(gòu)化的學習。為了突顯學生的主體地位，強調(diào)知識的理解與遷移，“體積”相關(guān)內(nèi)容的學情分析將分別從認知結(jié)構(gòu)的清晰性、辨析性、穩(wěn)定性三方面進行分析。（如圖1）

圖2 學生調(diào)研作品

通過梳理學生提到的度量屬性，大體分為生活中常見的量(質(zhì)量、溫度）、幾何的量（長度、角度、面積、體積、容積），還有一些不太熟悉的導出的量（速度、密度、濃度）。其中大部分學生都提到過“體積”這一詞。

隨后，教師以訪談的方式追問學生：“哪些是我們已經(jīng)能夠測量出來的呢？怎樣測量？請你舉例說一說。”學生說：“時間我們可以用鐘表來測量，比如一節(jié)課40 分鐘。”有的學生說：“測量溫度可以用溫度計，比如室溫是25 攝氏度。”還有的學生說：“人的質(zhì)量可以用稱來測量，我的質(zhì)量是40 千克。”有的學生說：“我用尺子可以測量出一本數(shù)學書的厚度是0.5 厘米。要求它的面積可以先測出長和寬，將長和寬然后相乘就可以得到。”

對“這些度量方法之間有沒有相同的地方？”這個問題，30 名學生，累計收集了46 次共同點。這些相同點的占比如圖3：

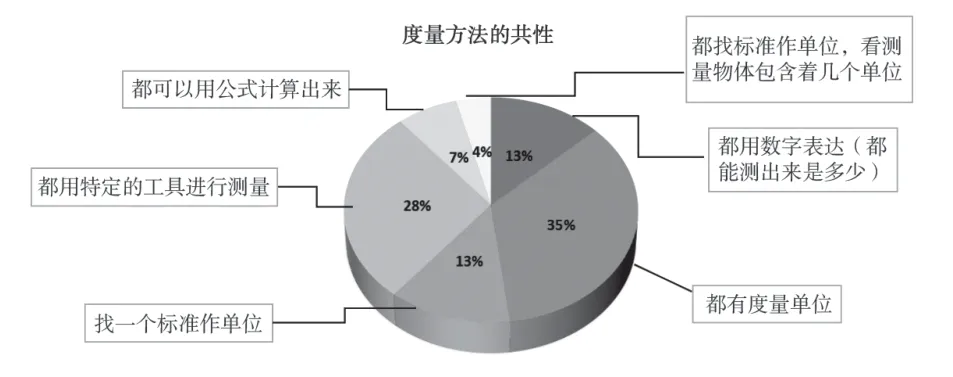
圖3 學生調(diào)研數(shù)據(jù)分布

調(diào)研學生：五年級30 名學生。

調(diào)研目的1：了解度量領域?qū)W習中，學生的原有認知。

題目1：生活中經(jīng)常遇到“測量”活動。比如，測量出一個蘋果的質(zhì)量約200 克；某學生的身高140 厘米；一間屋子的占地面積40 平方米；等等。你知道生活中還能測量些什么呢？

學生作答如圖2：

基于這樣的數(shù)據(jù)，教師發(fā)現(xiàn)學生提煉的共同點都是通過最直觀地觀察得到的表象特征，缺乏對度量方法本質(zhì)和共性之間關(guān)聯(lián)（即為什么會有這些共性）的深層次理解。由此，教師得到調(diào)研結(jié)果：一方面，學生有著豐富的度量經(jīng)驗，了解常見屬性的度量單位和度量工具，會簡單應用工具測出相應的數(shù)值。另一方面，在學生的認知結(jié)構(gòu)中，度量知識是碎片化的，沒有形成清晰的度量性概念的認知結(jié)構(gòu)。因此，在后續(xù)的教學中，我們應把“體積”單元的教學內(nèi)容嵌入更大的“度量”視角，經(jīng)歷類比、推理的思考過程，加深對度量本質(zhì)的理解，幫助學生構(gòu)建度量性概念的學習路徑。

調(diào)研目的2：了解易混概念學生是否產(chǎn)生認知沖突。

題目2：同學們聽說過體積嗎？什么是物體的體積？

97%的學生都聽說過“體積”這個概念。對于“什么是物體的體積？”這個問題，調(diào)研數(shù)據(jù)分布如圖4：

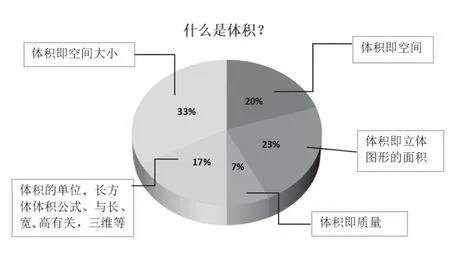
圖4 學生調(diào)研數(shù)據(jù)分布

基于這樣的數(shù)據(jù)分布，教師發(fā)現(xiàn)有20%的人認為體積就是空間，即沒有把體積歸為是用“數(shù)”去表達的量。還有部分學生對體積的理解，受到面積和質(zhì)量屬性的干擾。尤其是受到面積干擾，就像學生在接觸一維概念長度和二維概念面積時發(fā)生混淆，二維概念和三維概念之間，也發(fā)生了混淆。17%的同學沒有直接回答什么是體積，但模糊地描述了與體積相關(guān)的知識。當然，還有33%的學生說出了體積的含義。面對這樣的結(jié)果，教師后續(xù)設計體積的學習活動時，一是要關(guān)注體積概念的本質(zhì)，因為體積是可測屬性，要突顯體積是用數(shù)量去刻畫立體圖形的大小的；二是要關(guān)注學生質(zhì)量和面積屬性的干擾，在適當?shù)臅r候，設計容易產(chǎn)生認知沖突的活動內(nèi)容，引導學生在辨析中突破認知障礙，從而理解體積的概念。

調(diào)研目的3：了解學生是否具備自主遷移的學習能力。

在學生理解體積的概念后，教師想要進一步了解學生在以往度量知識的學習中，是否有一定的知識遷移意識與能力，因此設計如下題目。

題目3：結(jié)合長度、面積、角度的學習經(jīng)驗，你們覺得應該從哪些方面來研究體積？對每個方面的內(nèi)容有哪些猜想？

對于第一小問，學生能夠想到可以從體積單位、單位進率、體積計算公式、體積在生活中的應用四個方面進行研究。調(diào)研數(shù)據(jù)統(tǒng)計顯示（如圖5），大部分學生都能提出2 ～3 個方面，被提到最多的方面就是體積單位和體積計算公式。這表明多數(shù)學生能夠遷移長度、面積的知識結(jié)構(gòu)，進行體積單位、進率及體積公式和應用等方面學習規(guī)劃，但是思考不夠全面，需要在后面的學習活動中，繼續(xù)補充完善。同時，從學生的猜想中可以看出，多數(shù)學生猜想正確，具有一定的推理意識。

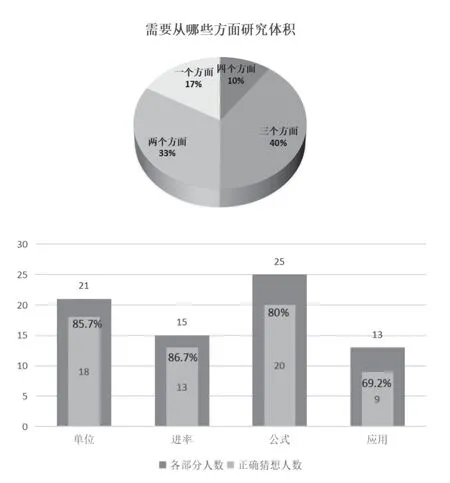
圖5 學生調(diào)研數(shù)據(jù)分布

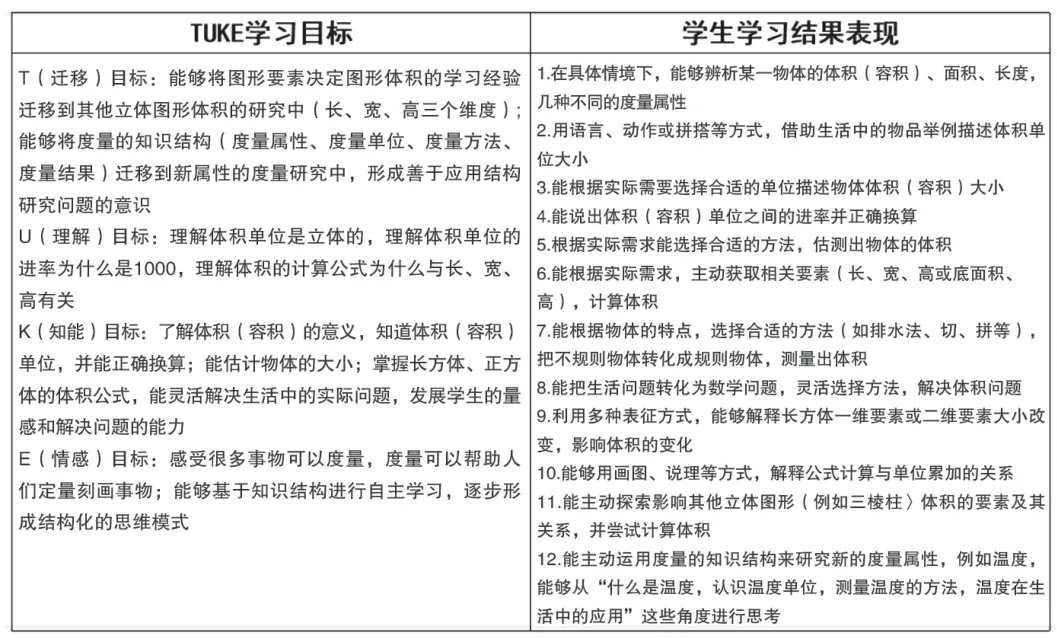
圖6 單元學習目標及結(jié)果表現(xiàn)

綜上分析，學生具備一定知識遷移的能力。在已有的研究中也曾指出，學生進入體積測量學習之前積累了大量的度量經(jīng)驗，無論是度量對象、度量方法，還是解決問題，都可以進行遷移式學習。因此，教師應充分借助學生已有的關(guān)于度量學習的認知結(jié)構(gòu)，引導學生自主規(guī)劃“體積”內(nèi)容的探究與推理。

三、單元學習目標及結(jié)果表現(xiàn)

基于以上分析，我們確定了以下單元學習目標及結(jié)果表現(xiàn)。在結(jié)果表現(xiàn)中，第1 ～8 條對應知能目標，第9 ～10 條對應理解目標，第11 ～12 條對應遷移目標。

四、學生思考的關(guān)鍵問題及學習任務序列

（一）學生思考的關(guān)鍵問題

由單元具體觀念衍生出的關(guān)鍵問題是學習任務的核心，是學生理解、感悟并形成單元具體概念的依托。確立關(guān)鍵問題，可以引導學生開展深度思考和合作交流，是“達到理解意義和自主遷移目標的關(guān)鍵”。基于“體積”單元具體概念，我們設計了本單元需要學生深入思考的三個關(guān)鍵問題。（如圖7）

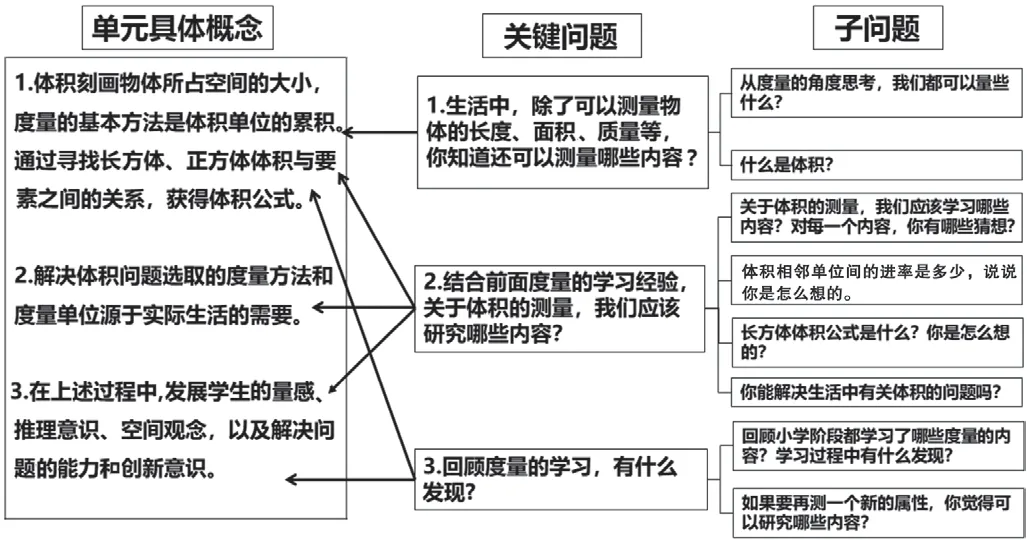
圖7 單元具體概念與關(guān)鍵問題

關(guān)鍵問題1 指向單元具體概念1。度量刻畫的是事物屬性的“大小”，其中體會被測事物的屬性對于學生是重要的，有時候還是困難的。這個關(guān)鍵問題重點就是思考度量屬性，下面對應著兩個子問題。子問題1，使學生關(guān)注一個度量對象具有不同的度量屬性。子問題2，從不同的度量屬性中聚焦三維空間的度量，認識體積。關(guān)鍵問題引領學生將體積概念的學習放置到度量領域的知識體系中，從更大的度量視角來認識體積，有助于學生建立度量性概念的知識結(jié)構(gòu)。

關(guān)鍵問題2 指向單元具體概念1，2，3。這個關(guān)鍵問題旨在借助已有度量認知結(jié)構(gòu)，促進學生運用遷移進行學習。首先遷移在長度、面積、角度學習中獲得的知識結(jié)構(gòu)，引導學生自主規(guī)劃體積的學習內(nèi)容。然后在規(guī)劃下展開結(jié)構(gòu)化的學習，聯(lián)系已有的度量學習經(jīng)驗分別研究體積單位，體積的基本度量方法，圖形要素與體積大小的關(guān)系，以及如何選擇合適的度量方法和單位解決實際問題。在規(guī)劃與研究的過程中，使學生不斷自我完善度量的認知結(jié)構(gòu)，發(fā)展學生的量感、推理意識、空間觀念，以及解決問題的能力及創(chuàng)新意識。因此在這個關(guān)鍵問題下對應著四個子問題，分別聚集如何規(guī)劃體積學習內(nèi)容；體積單位的研究；體積公式的猜想驗證；解決生活中的體積問題。

關(guān)鍵問題3 指向單元具體概念1 和3。在完成小學階段最后一次幾何度量學習后，在關(guān)鍵問題3 的引領下，通過兩個子問題，引導學生溝通不同屬性度量之間的聯(lián)系，豐富度量的認知體系，完善度量的認知結(jié)構(gòu)，并能將結(jié)構(gòu)自主遷移到新屬性的度量研究中，形成善于應用結(jié)構(gòu)研究問題的意識，發(fā)展學生的量感和推理意識。

在單元具體概念引領下，基于三個關(guān)鍵問題，研究團隊設計了學習任務序列。

（二）基于關(guān)鍵問題的學習任務設計框架

本單元共14 個學習任務，分6 課時進行教學（如圖8）。學習任務的設計體現(xiàn)度量的全過程，注重借助已有的度量認知結(jié)構(gòu)，促進學生在遷移中學習。（如圖9）

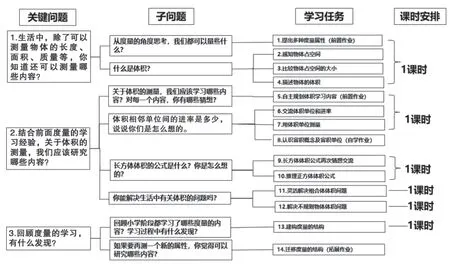
圖8 學習任務序列及課時安排

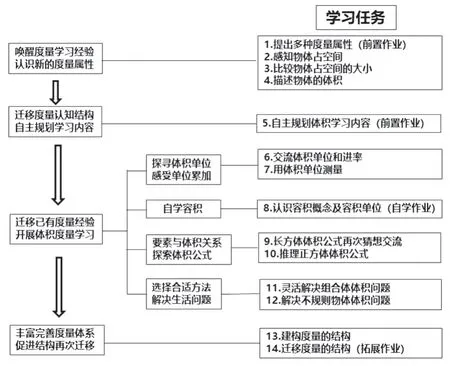
圖9 度量大概念引領下的學習任務序列

學習任務1 ～4 突出度量屬性，創(chuàng)設有關(guān)冰激凌的生活情境，提出多種度量屬性，在多種度量屬性中聚焦三維空間度量，在度量活動中感受立體圖形的三維屬性特點，認識到體積的大小是可量化的。學習任務5 規(guī)劃學習內(nèi)容，借助已有的度量認知結(jié)構(gòu)自主規(guī)劃，以利于展開結(jié)構(gòu)化的學習。學習任務6 ～7 關(guān)注度量單位，遷移長度單位和面積單位的學習經(jīng)驗，根據(jù)度量屬性先猜想，再統(tǒng)一體積單位的形狀、大小與進率，并能靈活選擇單位度量，再一次感受單位累加的基本度量方法。學習任務8 自學容積和容積單位。學習任務9 ～10 優(yōu)化度量方法，類比遷移長方形面積公式的學習經(jīng)驗，研究立體圖形的要素與體積的關(guān)系，獲得長方體、正方體體積公式。學習任務11 ～12 解決生活問題，根據(jù)實際需要，選擇合適的度量方法解決問題。學習任務13 ～14 回顧梳理反思，溝通不同度量屬性間的聯(lián)系，豐富度量體系，完善度量的認知結(jié)構(gòu)，并能遷移到新屬性的度量研究中，形成結(jié)構(gòu)化學習的意識。

（三）設計特色說明

1.在多屬性測量中，激活度量經(jīng)驗

無論是幾何領域中的長度、面積、體積等概念，還是生活中常見的量，比如溫度、時間、質(zhì)量等，都具有用“數(shù)”去刻畫大小的本質(zhì)。因此“體積”單元的設計起點并沒有從研究體積概念直接入手，而是先將“體積”這一概念嵌入更大的度量知識體系中，體會度量的一致性。教學時創(chuàng)設冰激凌的情境，引導學生借助熟悉的“量”，如可以測量冰激凌的質(zhì)量、冰激凌杯子的表面積、冰激凌的溫度等，喚醒度量經(jīng)驗，為后續(xù)自主研究體積或其他屬性相關(guān)內(nèi)容做好鋪墊。

2.在自主規(guī)劃中，遷移度量結(jié)構(gòu)

基于課前的學情調(diào)研， 可以發(fā)現(xiàn)多數(shù)學生能夠遷移長度和面積研究的內(nèi)容，自主規(guī)劃出研究體積需要從哪些方面入手。課堂中通過學生之間的交流、補充和啟發(fā)，學生意識到無論長度、面積、還是體積，都需要研究他們各自的單位、進率、計算公式以及靈活解決問題等方面的內(nèi)容。這樣的自主規(guī)劃，不僅實現(xiàn)了對體積這一數(shù)學概念與相關(guān)知識的理解，也引導學生進一步關(guān)注一維（長度）、二維（面積）、三維（體積）之間的聯(lián)系，完善幾何領域的度量認知。

3.在梳理反思中，豐富度量體系

怎樣將幾何領域的度量結(jié)構(gòu)拓展到更大的一般性度量結(jié)構(gòu)中？和本單元的起始學習任務形成呼應，從一般性度量經(jīng)驗中走進體積的學習，最終還要回到對一般性度量的認識與反思。學生用喜歡的方式整理所有度量學習的發(fā)現(xiàn)與再認識。在這些度量內(nèi)容中，既要梳理長度、角度、面積、體積四次幾何度量學習與發(fā)現(xiàn)，還要尋找小學階段其他常見的量之間的聯(lián)系，從而豐富度量體系，形成結(jié)構(gòu)化思考問題的一般方式，實現(xiàn)真正意義上的自主遷移。