某埋頭彈機槍撥彈杠桿動力學分析及優化

劉 強, 周克棟, 李東昊, 陸 野, 赫 雷, 任海鉞

(1.南京理工大學 機械工程學院, 南京 210094; 2.國營第二九六廠, 重慶 400050)

某埋頭彈機槍采用了彈膛與槍管分離的擺膛機構,用以發射塑料彈殼的埋頭彈。為了實現該槍的發射功能,將該槍后坐過程中的機構動作依次安排為開鎖、擺膛、抽動推彈桿、輸彈,其中輸彈動作是本槍械后坐過程中的最后一個機構動作,前面三個機構動作在完成過程中消耗的自動機行程均很長,且四個機構動作必須依次完成,相互之間不能有交疊部分。考慮到全槍總長有限,故該槍在完成輸彈過程中,主動件槍機框的行程很短,如不對輸彈機構進行優化設計,則輸彈機構難以平穩運行。因此,本文對撥彈杠桿曲線槽理論輪廓線進行優化設計,并對輸彈機構的動力學特性進行分析。

對于傳統機槍輸彈機構的設計及動力學分析,前人已經做了很多研究及優化,王瑞林等[1]出于對某機槍人機功效的考慮,為了降低槍械首發裝填的阻力,優化了某機槍輸彈機構的大杠桿曲線;靳天佑等[2]以輸彈機構在輸彈過程中消耗自動機的動能為目標函數,求出了撥彈杠桿的最優解;姜奧等[3]通過優化輸彈機構的傳速比,減少了撥彈滑板的加速度;李洪強等[4]詳細研究了輸彈過程中輸彈阻力的變化規律;李世康等[5]選用5次函數曲線優化了高射速轉管炮的凸輪曲線,但他僅用到了五次函數曲線的平滑性,并未從機構力學特性入手,優化5次函數曲線。本槍所面臨的主要矛盾與前面所述文獻不同,需要在更短行程內完成輸彈動作,傳動件相互撞擊接觸力更大,工況更為惡劣。

1 輸彈機構結構特點

本槍采用了凸輪杠桿的撥彈方式,輸彈機構如圖1所示。

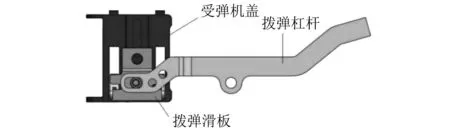
圖1 輸彈機構Fig.1 Feed transfer mechanism

本槍械所采用的輸彈機構即傳統的單程輸彈機構,在槍機框后坐時,由槍機框上的導柱帶動撥彈杠桿回轉,撥彈杠桿帶動撥彈滑板平動完成輸彈動作。

在研究過程中,發現本槍械撥彈杠桿中實際起到撥彈作用的曲線槽部分很短,這是埋頭彈槍撥彈行程過于靠近槍機框后坐結束所致。現將同口徑88式5.8 mm通用機槍《自動循環圖》[6]中的撥彈行程圖部分與本文所述某埋頭彈機槍對比,對比圖如圖2所示。

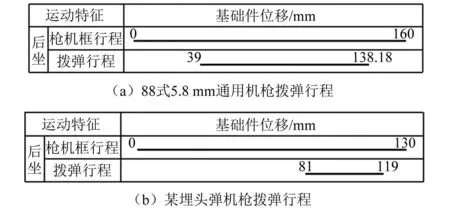
圖2 撥彈行程對比Fig 2 Comparison of cartridge transferring travel

由圖2對比可以看到,88式5.8 mm通用機槍槍機框后坐總行程160 mm,槍機框后坐位移到達39 mm時,即開始帶動撥彈機構進行撥彈,整個撥彈行程達99.18 mm;而本文所述某埋頭彈機槍槍機框后坐總行程130 mm,直到槍機框后坐位移到達81 mm時才開始撥彈,整個撥彈行程僅有38 mm。由于某埋頭彈機槍的撥彈行程短,撥彈杠桿曲線部平均斜率大,故工況相較于88式5.8 mm通用機槍更為惡劣。

在最初采用直線段作為某埋頭彈機槍撥彈杠桿曲線槽理論輪廓線(下文簡稱“理論輪廓線”)時,造成槍機框導柱進入杠桿曲線槽時對輸彈機構的沖擊很大。這種沖擊會造成三個不利影響:①槍機框導柱進入撥彈杠桿曲線槽的過程中,槍機框速度會急劇下降,造成槍機框后坐能量不足;②槍機框導柱對撥彈杠桿的沖擊引起連鎖反應,使得輸彈機構其他相關零部件之間也產生沖擊,造成輸彈機構中較薄弱的零件過早達到使用壽命或直接被損壞;③槍機框導柱瞬間沖擊撥彈杠桿,使得撥彈杠桿帶動撥彈滑板瞬間移動,撥彈滑板上鉸接的撥彈齒瞬間撥動輸彈機座上的塑料彈殼埋頭彈,可能造成彈殼外表面被撞傷,產生安全隱患。因此,輸彈機構工作平穩,降低槍機框導柱進入撥彈曲線槽時對輸彈機構的沖擊,是優化理論輪廓線的關鍵所在。

2 優化目標的確定

在機槍實際發射過程中,需要扣合輸彈機蓋,此時受彈機座上還有彈鏈,彈鏈完全遮擋了撥彈齒、撥彈滑板等結構,因此無法用高速攝影設備記錄輸彈機構的運動曲線。但高速攝影可以拍攝槍機框的運動過程,從而得到槍機框的運動曲線。因此,關于輸彈機構中撥彈杠桿、撥彈滑板的運動必須依靠試驗、仿真相結合的方式得到,即將試驗得到的槍機框速度曲線與仿真得到的槍機框速度曲線相互對比,當仿真結果在可接受的誤差范圍內時,可認為仿真獲得了真實情況,此時,在試驗中難以測得的數據可以從仿真結果中間接獲得。

將本文所研究的埋頭彈機槍夾持在固定槍架上,并進行射擊試驗,用高速攝影設備拍攝槍機框運動過程,提取出槍機框后坐速度—時間曲線,然后將該試驗所得曲線與仿真得到的速度—時間曲線進行對比,對比如圖3所示。

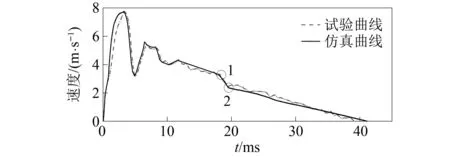
圖3 槍機框速度實測、仿真對照Fig.3 Actual measurement and simulationcomparison of bolt carrier speed

圖3中,實測速度—時間曲線與仿真速度—時間曲線的關鍵值對比如表1所示。

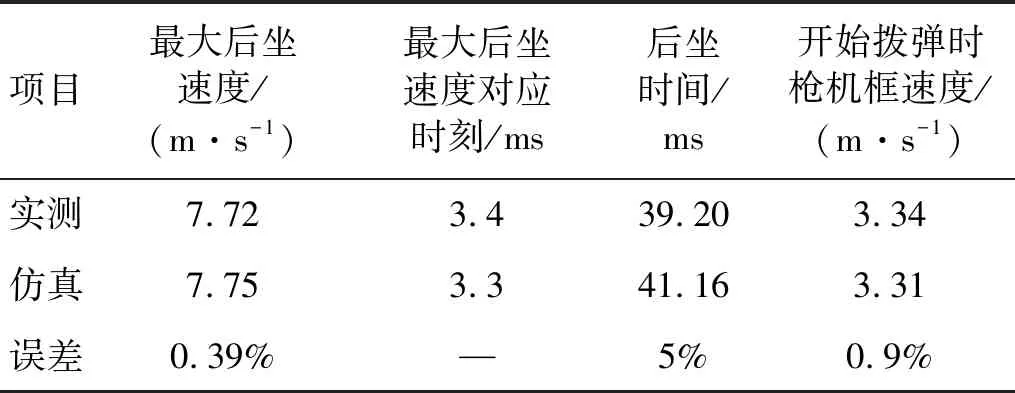
表1 槍機框速度—時間實測、仿真關鍵值對照

由表1可以看出,槍機框速度—時間曲線關鍵值的實測值與仿真值的誤差≤5%,可以認為埋頭彈機槍仿真結果較為真實地反映了槍機框實際運動的特點,因此可以將仿真得到的輸彈過程中的關鍵數據提取出來,用于分析本埋頭彈機槍輸彈機構的動力學特性。圖3中:槍機框速度到達點1時,槍機框導柱開始進入撥彈杠桿曲線槽;點1到點2的過程即槍機框導柱與撥彈杠桿曲線槽起始段相互撞擊的過程。可見,在這個過程中,槍機框速度有所損失,損失為0.94 m/s。

因仿真較為準確地描述了槍機框的運動規律,可由仿真結果提取出槍機框導柱與撥彈杠桿曲線槽之間的相互作用力及撥彈杠桿的角速度—時間曲線、該作用力及槍機框速度—時間曲線。曲線如圖4、圖5所示。

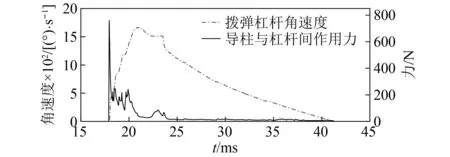
圖4 撥彈杠桿角速度及導柱與撥彈杠桿間作用力Fig.4 The angular speed of the belt feed lever and the force between the guide post and the belt feed lever

圖5 槍機框速度及導柱與撥彈杠桿間作用力Fig.5 The speed of bolt carrier and the force between the guide post and the belt feed lever

由圖4、圖5可以看出,槍機框導柱在進入撥彈杠桿曲線槽的一瞬間,與撥彈杠桿間作用力很大,為757 N,而后,在整個撥彈過程中,導柱與撥彈杠桿之間的相互作用力并不大,最高僅為200 N左右,這是由于槍機框導柱進入撥彈杠桿曲線段時,傳速比突變引起的,因此,必須優化設計撥彈杠桿,使得槍機框導柱進入撥彈杠桿曲線時,傳速比變化連續,且降低槍機框導柱對撥彈杠桿的沖擊力。

本文對撥彈杠桿曲線槽的理論輪廓線進行優化,選取撥彈過程中導柱對撥彈杠桿的最大沖擊力最小為目標函數,通過算法優化,尋求目標函數最小時對應的曲線槽理論輪廓線。

3 撥彈杠桿優化設計過程

3.1 優化參數的確定

基于槍械結構的約束,以及撥彈滑板運動行程的約束,理論輪廓線的起始坐標與終點坐標均已確定,優化的目的在于優化理論輪廓線的形狀。由機械原理可知,凸輪理論輪廓線的形狀決定從動件的運動規律,從動件常見的運動規律有:等速運動、等加速等減速運動、簡諧運動、正弦加速運動、多項式運動規律等。根據以上運動規律,理論輪廓線形狀的選取有多種方式,而多項式運動規律通用性較強,可以適應較多的運動特性。因此,本文采用五次函數曲線作為理論輪廓線的形式,五次函數曲線槽迫使運動件加速度連續,理論上不存在沖擊[7],五次函數曲線的表達式為

(1)

式中:x1,y1為理論輪廓線上點的坐標;坐標原點O1在理論輪廓線的起始點,如圖6所示。

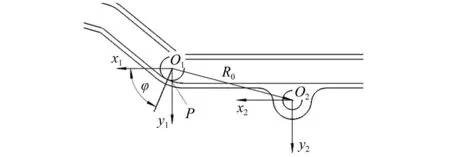
圖6 撥彈系統坐標系Fig.6 The coordinate system of the cartridge feeding system

因坐標原點在理論輪廓線的起始點,即理論輪廓線過(0,0)點,故式(1)中a0=0;又因為導柱進入撥彈杠桿曲線槽時,需要消除剛、柔性沖擊,因此曲線在x1=0時,式(1)的一、二階導數均為0,即,a2=a1=0。至此,待確定參數為a3～a5的值,因為輸彈機構的結構參數已知,即五次函數曲線的終點坐標(p,q)已知,在曲線上再取兩個點(p/3,y11),(2p/3,y12),y11與y12均為未知數,若知道y11、y12的值,就可由曲線終點坐標及所取兩個點的坐標求解a3～a5的值,進而求出五次函數曲線的具體形式。

3.2 優化中的基本假設

本文對撥彈杠桿的優化將基于機構的動力學特性進行,為了建立相對準確的動力學模型,做出如下假設:

①槍機框導柱撥動撥彈杠桿的過程中,導柱與撥彈杠桿間的撞擊普遍存在,本文將理論輪廓線離散為點集,并取兩者間的撞擊次數為曲線的離散點數,事實上,本文將撥彈杠桿曲線槽實際輪廓線離散為321個點,并對每個點上,槍機框導柱是否對撥彈杠桿造成沖擊進行了判別,因此,這種處理方式較為準確地模擬了槍機框導柱與撥彈杠桿之間相互撞擊的情況;

②撞擊是瞬間完成的,在導柱對撥彈杠桿的撞擊過程中,不考慮撥彈阻力及其他阻力對撞擊的影響,所有阻力消耗的能量均在運動方程中考慮;

③撞擊模型為純彈性模型,不考慮撞擊中的能量損失,撞擊后,對撞物體可以瞬間恢復形變。

3.3 輸彈機構接觸分析

為了描述撥彈杠桿曲線槽實際輪廓線的形狀,現建立坐標系(見圖6)。

由圖6可知,從槍機框上的導柱進入撥彈杠桿開始分析,在導柱截面圓心位置,即理論輪廓線起點O1位置建立定坐標系O1x1y1,x1軸指向為槍機框后坐方向。

在撥彈杠桿回轉中心O2建立定坐標系O2x2y2,x2軸方向與x1軸平行。

在撥彈杠桿回轉中心建立隨動坐標系Ocxcyc,該隨動坐標系與撥彈杠桿固連,在t=0時刻,Ocxcyc與O2x2y2重合。

假設導柱與撥彈杠桿的接觸點為P,O1P與x1軸的夾角為φ,則P點在坐標系O1x1y1中的矢徑為

R1=(s+r0cosφ,r0sinφ)T

(2)

式中:s為導柱位移,即槍機框位移;r0為導柱外圓半徑。

假設O1到O2的距離矢量為R0=(-a,b),則P點在定坐標系O2x2y2中的矢徑R2為

R2=R1-R0=(s+a+r0cosφ,r0sinφ-b)T

(3)

假設在t時刻,撥彈杠桿回轉角度為τ,則在動坐標系Ocxcyc中,P點的矢徑Rc為

Rc=ER2

(4)

式中,E為坐標變換矩陣,有

(5)

由以上諸式可以得到Rc的具體矩陣,矩陣中τ與s均為時間t的函數,知道τ和s的表達式,就可以知道撥彈杠桿曲線槽理論輪廓線的函數表達式。

由上述方法求出的曲線方程,為該類曲線的曲線族方程,要進一步確定曲線的具體形式,就需要確定φ與曲線形狀的關系,即需要滿足接觸方程。由于導柱外圓與曲線槽曲線均光滑,根據微分幾何包絡理論,它們之間的接觸方程為

R12·n1=0

(6)

式中,V12為凸輪輪廓曲線與導柱輪廓曲線之間的相對滑移速度,n1為導柱輪廓曲線在接觸點的單位法向量,關于式(6)的詳細計算過程,參見參考文獻[7],由式(6)得

(7)

(8)

式中:v為槍機框后坐的平移速度;ω為撥彈杠桿擺動的角速度;s為槍機框位移;k為傳速比,可以看出,具體到曲線上某點時,φ只與結構尺寸、槍機框位移及傳速比有關,而傳速比由理論輪廓線方程決定。

3.4 輸彈機構運動分析

輸彈過程中,除了槍機框、撥彈杠桿在運動,一起參與運動的還有撥彈滑板、彈鏈等零部件,為了研究撥彈滑板的運動,現對撥彈杠桿的尺寸標記如圖7所示。

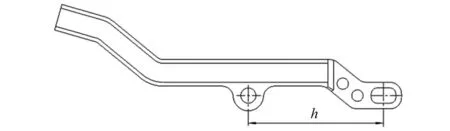
圖7 撥彈杠桿尺寸標記Fig.7 Dimension marking of belt feed lever

在本槍械中,撥彈滑板只能做一個方向的平移運動,假設撥彈滑板的平移速度為vH,則有

vH=ωhcosτ=kvhcosτ=rv

(9)

式中:ω為撥彈杠桿擺動角速度;k為傳速比;v為槍機框后坐速度;τ為撥彈杠桿擺過的角度,r=khcosτ。

在槍機框帶動撥彈機構運動的過程中,符合能量守恒定律,根據能量守恒定律,可以列出槍機框及撥彈桿桿的運動方程為

(10)

式中:MA為槍機框質量;MB為從動件(包括撥彈滑板、撥彈齒、彈鏈)的質量;JB為撥彈杠桿的轉動慣量;vA為槍機框位移為x時的速度;vA0為供彈階段開始時槍機框的運動速度;PA為作用到槍機框上的火藥燃氣的壓力;FA和FB為作用到槍機框和從動件上的阻力;ηp為傳動效率;k0為供彈階段開始時的傳速比,k0=0;

ηp取常數0.8;FA為復進簧簧力,由復進簧參數求得;FB為撥彈阻力,從仿真結果讀取。如若知道撥彈杠桿曲線段理論輪廓線的方程,即可知道槍機框導柱運動到曲線槽任意位置時的傳速比,進而可由式求出槍機框在任意位置時的速度vA。

3.5 法向接觸碰撞力模型

本文中采用Hertz接觸理論計算導柱與撥彈杠桿相互碰撞時產生的碰撞力,該模型認為接觸力是壓入深度的非線性函數,且碰撞后參與部件可以彈性恢復,不存在能量損失,接觸力表達式為[8]

Fn=Kδn

(11)

式中:δ為兩個接觸剛體之間的相對壓入量;K為接觸剛度系數;n為力指數,由接觸剛體的材料和接觸區域的幾何特性決定,對于金屬接觸,n值取1.5。剛度K的計算式為[9]

(12)

式中:Ri與Rj分別為導柱的半徑和導柱與撥彈杠桿接觸點的曲率半徑;σi、σj與導柱、撥彈杠桿的材料參數有關,其計算式為

(13)

式中,vl,El分別為材料的泊松比和彈性模量。

假設導柱每次與撥彈杠桿撞擊以后,撥彈杠桿回轉一個角度Δτ,即在曲線槽實際輪廓線第i點,導柱與撥彈杠桿撞擊之前,撥彈杠桿的回轉角度為τi-1,撞擊之后為τi,有

Δτ=τi-τi-1

(14)

同理,在第i點發生撞擊之前,槍機框后坐的速度為vAi-1,撥彈杠桿回轉的角速度為ωi-1,撥彈杠桿上與導柱接觸點的速度為vBi-1;發生撞擊之后,槍機框后坐的速度為vAi,撥彈杠桿回轉的角速度為ωi,撥彈杠桿上與導柱接觸點的速度為vBi。槍機框導柱與撥彈杠桿之間的撞擊就是槍機框為撥彈杠桿傳速的過程。撞擊前,撥彈杠桿在接觸點Pi的速度方向如圖8所示。

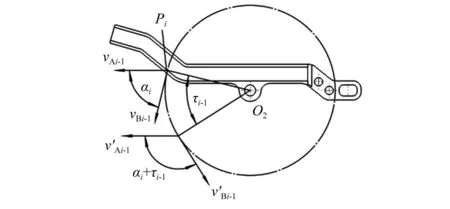
圖8 撥彈杠桿與導柱接觸點速度方向Fig.8 Speed direction of the contact point between the belt feed lever and the guide post

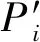
如圖9所示,在Pi點,導柱與撥彈杠桿接觸力的方向為O0Pi方向(見圖6),在t=0時,O0與O1重合,O0為導柱圓心,O0Pi與槍機框后坐方向的夾角為φi,那么,撥彈杠桿上Pi點速度方向與O0Pi的夾角為αi+τi-1-φi,由Pi與O2的坐標求出O2Pi的長度為li,則此時導柱速度vAi-1與撥彈杠桿上Pi點的速度vBi-1在O0Pi方向的投影、分別為

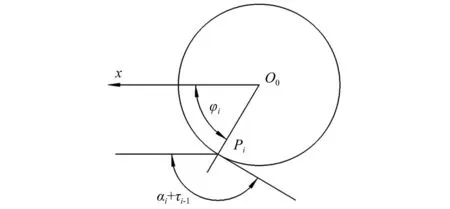
圖9 接觸點速度方向與接觸力方向夾角示意圖Fig.9 Schematic diagram of the angle between the speed direction of the contact point and the direction of the contact force

(15)

兩者的差值即在Qi點的O1Qi方向,導柱相對于撥彈杠桿的速度

(16)

式中,若Δv>0,則為導柱撞擊撥彈杠桿,撞擊力由式(17)及式(11)計算;參見式(11),由能量守恒即可求出導柱與撥彈杠桿間的最大穿透深度μ

(17)

將求得的最大穿透深度μ代回式,則可以求出兩者間的最大穿透力Fnm,即為所求撞擊力。

式(16)中,若Δv<0,則為撥彈杠桿撞擊導柱,撞擊面不在所求面上,又因為撥彈杠桿質量遠小于槍機框質量,撥彈杠桿對導柱的撞擊力可以忽略不計,因此直接取Fnm=0,事實上,輸彈機構在輸彈過程中受到的阻礙更多,阻力大,質量小,因此,撥彈杠桿每次被導柱撞擊后,撞擊增加的速度很快就會降下來,一般不會出現Δv<0的情況。

3.6 優化過程

本文采用遺傳算法[10]對所求的撥彈桿曲線槽理論輪廓線進行優化,其具體優化過程為:如2.1節所述,首先由遺傳算法的賦值程序為y11、y12賦值,求出第一代五次函數曲線方程,并將該曲線離散為321個點。當槍機框導柱圓心處于第i點時,理論輪廓線與導柱圓心重合點Qi的坐標為(xi,yi),Qi到撥彈杠桿回轉中心O2的距離為ji,但此時需要按照前一個重合點Qi-1求解出撞擊前撥彈杠桿的回轉角度τi-1,Qi-1到撥彈杠桿回轉中心O2的距離為ji-1,τi-1如圖10所示。

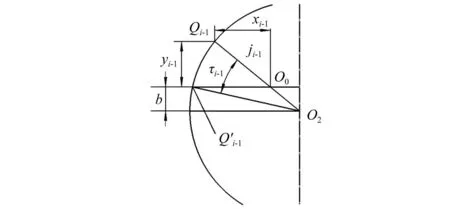
圖10 撥彈杠桿回轉角度示意圖Fig.10 Schematic diagram of rotation angle of belt feed lever

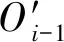
(18)

式中,b值為3.3節中所述b值。取導柱在第i-1(i≥3)點時,導柱與撥彈杠桿間的傳速比為ki-1,有

(19)

將式(19)代入運動方程式(10),可以求出導柱在第i-1點完成傳速后的后坐速度vAi-1及撥彈杠桿的回轉角速度ωi-1,然后由2.5節中的方法,先求出理論輪廓線在i點的曲率半徑,進而求出導柱與撥彈杠桿在i點的撞擊力FNi,因為曲線被離散為321個點,除第一個點(第一個點傳速比為0,回轉角為0,默認無沖擊)外,可以求出320個撞擊力FNi(第二個點的沖擊載荷由槍機框導柱進入曲線槽時的速度單獨求出),取其中最大的一個撞擊力值FNmax為一次計算的返回值,用遺傳算法不斷迭代,即不斷更換五次函數曲線的方程,求FNmax的最小值,直至算法收斂,此時FNmax所對應的五次函數曲線即為所求的最優曲線。

4 優化結果

將優化后的結果與優化前的結果相比較,有撥彈杠桿曲線槽理論輪廓線的對比如圖11所示。

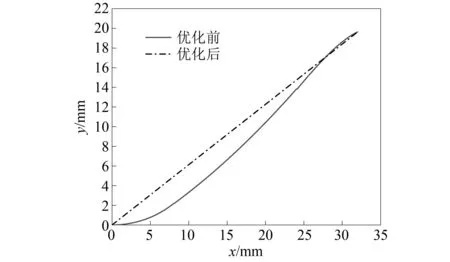
圖11 優化前后撥彈杠桿理論廓線展開線對比圖Fig.11 Comparison of the theoretical profile of the belt feed lever before and after optimization

從圖11可以看出,撥彈杠桿曲線槽起始段明顯較為平緩,理論輪廓線斜率從0開始逐漸增大,使得槍機框導柱進入撥彈杠桿曲線槽時,理論上沒有沖擊。

按照圖11所得的優化后理論輪廓線重新進行動力學仿真,得到槍機框速度-時間及導柱、撥彈杠桿間沖擊力的曲線如圖12所示。

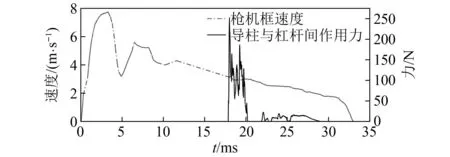
圖12 優化后,槍機框速度及導柱與撥彈杠桿間作用力Fig.12 The speed of bolt carrier and the force between the guide post and the belt feed lever after optimization

按照圖11所示理論輪廓線重新加工撥彈杠桿,并做射擊試驗,將兩次試驗得到的槍機框速度圖線進行對比,對比圖線如圖13所示。

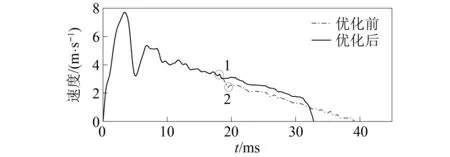
圖13 撥彈杠桿曲線槽優化前后槍機框速度對比圖Fig.13 Comparison diagram of the bolt carrier speed before and after the optimization of the curve slot of the belt feed lever

結合圖13、圖14及前文中的圖3,在理論輪廓線優化前,槍機框導柱進入撥彈杠桿曲線槽時,速度從點1下降到點2,速度損失為0.94 m/s;優化后,該過程中,速度從點1下降到點3,速度損失為0.28 m/s。優化后的速度損失為優化前的29.79%。

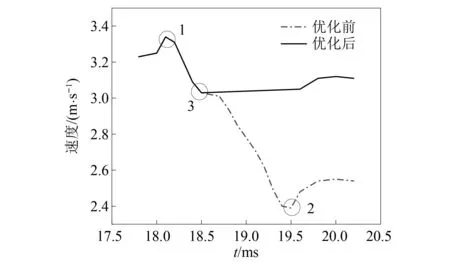
圖14 圖13局部放大圖Fig.14 Partial enlarged view of figure 13

將修改后的撥彈杠桿重新代入仿真計算,得到優化前后,槍機框導柱進入撥彈杠桿曲線槽時,導柱對撥彈杠桿的沖擊對比,如圖15所示。

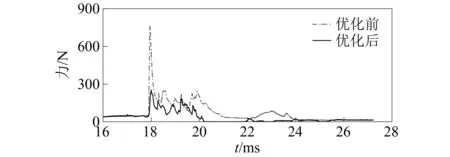
圖15 優化前后導導柱對撥彈杠桿沖擊力對比Fig.15 Comparison of the impact force of the guide post on the belt feed lever before and after optimization

優化后,最大沖擊力由優化前的757 N降低到了252 N,導柱進入撥彈杠桿曲線的沖擊力約等于原來的1/3,可見,用控制碰撞力的方法,達到了優化的目的。

5 結 論

本文針對槍機框導柱進入撥彈杠桿曲線槽時沖擊大,槍機框速度下降嚴重進行了研究分析,并對撥彈杠桿曲線槽的理論輪廓線進行了優化設計,利用槍械射擊試驗驗證了優化結果的可信性及有效性,得出以下主要結論:

(1)通過建立動力學模型,可以較為準確地模擬槍械實際后坐過程,從而從仿真結果中提取出試驗難以測量得到的數據。

(2)采用五次函數曲線作為撥彈杠桿曲線槽理論輪廓線的曲線形狀有利于降低導柱進入彈膛螺旋槽時的沖擊。

(3)通過將理論輪廓線離散為點集的形式,可以通過Hertz接觸理論計算出導柱在每個點上撥彈杠桿曲線槽之間的撞擊力,從而檢索出導柱與曲線槽相互作用過程中的最大撞擊力。

(4)通過遺傳算法優化撥彈杠桿曲線槽理論輪廓線的具體形狀,使導柱與曲線槽之間的最大撞擊力最小,即得到本文所需要的最優曲線。按照最優曲線形狀重新加工撥彈杠桿槽,并做試驗,得出導柱在與撥彈杠桿曲線槽相互作用的整個過程中,槍機框速度損耗由優化前的0.91 m/s降低到優化后的0.28 m/s。并由仿真分析得出,優化后,導柱與撥彈桿桿曲線槽之間的最大沖擊力降低為優化前的1/3,達到了優化目的。