調(diào)制光學(xué)參量放大器對雙機械振子量子糾纏與壓縮的影響

杜宏杰，郭金良

（天津師范大學(xué)物理與材料科學(xué)學(xué)院，天津 300387）

腔光力系統(tǒng)[1]是研究量子力學(xué)特性由介觀尺度到宏觀尺度的一種方法，其主要研究對象是機械振子與光腔間可控的輻射壓力相互作用.近年來，憑借潛在的應(yīng)用價值和前沿的研究成果，腔光力系統(tǒng)成為應(yīng)用工程科學(xué)和基礎(chǔ)研究科學(xué)的有力平臺.此外，量子糾纏作為量子物理學(xué)的基石，在量子理論基礎(chǔ)和量子信息處理等潛在應(yīng)用中具有重要的作用[2].宏觀糾纏不僅可以幫助科研人員闡明宏觀自由度由經(jīng)典世界到量子體系的轉(zhuǎn)變[3-5]，而且在連續(xù)變量系統(tǒng)中也是重要的資源[6-7].因此，制備宏觀糾纏具有重要的意義.目前，已有研究在各種光學(xué)機械裝置中提出許多方案來產(chǎn)生量子糾纏，如通過光（微波）場與一個可動鏡間的直接輻射-壓力耦合產(chǎn)生光（微波）-機械糾纏[8]，但該光-機械糾纏容易被系統(tǒng)的熱噪聲破壞.Mari 和Eisert[9-10]通過將周期性調(diào)制驅(qū)動場引入經(jīng)典光機系統(tǒng)極大地增強了光機糾纏，但受限于系統(tǒng)的穩(wěn)定性，糾纏強度仍無法超過1 ebits 的穩(wěn)態(tài)糾纏極限.此外，還有一種宏觀糾纏是2 個機械振子間的機械-機械糾纏，由于早期基于直接輻射-壓力相互作用方案制備所得機械-機械糾纏較脆弱[11-12]，研究人員在光機系統(tǒng)中應(yīng)用了如直接機械耦合、壓縮真空光輸入、單光子強耦合或周期調(diào)制泵浦等技術(shù)，但糾纏的增強量并不顯著.近年來，研究人員提出許多使2 個力學(xué)振子產(chǎn)生糾纏的方案，如利用糾纏交換[13]、使用壓縮光驅(qū)動雙腔[14]以及注入一對糾纏光束到獨立的2 個光學(xué)腔[15].Joshi 等[16]利用光纖對2 個不同的Fabry-Perot 腔進行耦合，但所得力學(xué)糾纏很小且受限于很低的熱溫度.Chen 等[17]利用周期性調(diào)制驅(qū)動，使由2 個力學(xué)模組成的光學(xué)腔壓縮復(fù)合模產(chǎn)生了較強的力學(xué)糾纏.實現(xiàn)宏觀振子的壓縮對精密測量的科學(xué)研究非常重要.近年來，研究人員通過各種非線性方案實現(xiàn)了機械振子的穩(wěn)態(tài)壓縮，如機械振子固有的非線性[18]以及系統(tǒng)中內(nèi)在的非線性耦合[19]或非線性介質(zhì)[20]等.Lu 等[21]利用非線性機械振子在腔光力系統(tǒng)中成功引入機械非線性，將系統(tǒng)動力學(xué)線性化，構(gòu)造有效哈密頓量制備機械壓縮.此外，熱庫方案通過不同頻率的2 個激光場驅(qū)動系統(tǒng)將哈密頓量線性化設(shè)計為非對稱的Rabi 型相互作用，實現(xiàn)了機械振子的穩(wěn)態(tài)強壓縮[22].

非線性介質(zhì)與光機系統(tǒng)的組合效應(yīng)使得強壓縮的制備變得容易，并取得了實質(zhì)性進展，如二階非線性簡并光學(xué)參量放大器（OPA）在產(chǎn)生壓縮光方面效果良好[23].實驗表明，放置在腔內(nèi)部的OPA 可以極大地增強機械冷卻，產(chǎn)生強的機械壓縮，并將單光子的光機耦合強度提升到強耦合狀態(tài)，提高檢測光機位置的精度[24-27].Hu 等[28]通過調(diào)制OPA 增強機械糾纏，并將周期調(diào)制腔驅(qū)動和OPA 的參數(shù)驅(qū)動聯(lián)合，在腔光機系統(tǒng)中實現(xiàn)了雙重機械壓縮[29]，但有關(guān)2 個機械振子間宏觀機械-機械糾纏的研究相對較少.

基于這種聯(lián)合驅(qū)動效應(yīng)的良好效果，本研究主要討論了在施加OPA 的腔光力系統(tǒng)中，OPA 對雙機械振子量子糾纏和壓縮的影響.通過對系統(tǒng)相關(guān)參數(shù)的討論以及求解系統(tǒng)穩(wěn)態(tài)的動力學(xué)演化，分析調(diào)制OPA對力學(xué)糾纏和壓縮的影響.

1 模型與哈密頓量

圖1 為由2 個機械振子和簡并的光學(xué)參量放大器（OPA）組成的復(fù)合腔光力系統(tǒng).

圖1 腔光力系統(tǒng)示意圖Fig.1 Schematic diagram of the cavity photomechanical system

圖1 系統(tǒng)中，2 個機械振子通過輻射壓力同時與1 個光腔耦合.機械振子的質(zhì)量為m，頻率為ωm，耗散為γm，頻率為ωc、衰減率為κ 的光腔被頻率為ωl、強度為E 的激光場驅(qū)動.此外，置于光腔中的OPA 被頻率為2ωp的泵浦激光驅(qū)動，其產(chǎn)生的參量增益為Λeiθ，該增益由泵浦激光的強度和相位共同決定.以驅(qū)動激光頻率ωl為旋轉(zhuǎn)框架，系統(tǒng)哈密頓量可以寫為（hˉ=1）

式（1）中：△0=ωc-ωl和Ω =2ωp-2ωl分別為光腔和簡并光子相對于驅(qū)動激光的失諧量；a 和a?為腔模的產(chǎn)生和湮滅算符；qj和pj分別為2 個振子的坐標(biāo)和動量算符，滿足對易關(guān)系[qj，pj]=ihˉ；g 為由輻射壓力引起的光腔和機械振子間的單光子光力耦合強度.

考慮到系統(tǒng)的耗散和漲落，式（1）中復(fù)合光力系統(tǒng)的動力學(xué)可用一組朗之萬方程（QLEs）描述，δO/δt=i[H，O]+N-Hdiss，其中N 為量子噪聲算符，Hdiss描述系統(tǒng)的耗散，O=pj，qj，a 為表征系統(tǒng)的算符，

式（2）中：ain（t）為平均值為0 的腔場輸入噪聲算符，滿足關(guān)聯(lián)函數(shù)〈〉= δ（t - t′）[19]；ξj（t）為作用于機械振子的熱噪聲算符；在高品質(zhì)機械振子極限下Q≡ωm/γm>>1，滿足馬爾可夫近似，即〈ξj（t）ξj（t′）+ξj（t′）ξj（t）〉/2 = γm（2nm+ 1）δ（t - t′）[30]，且nm=[exp（hˉωm/kBT）-1]-1表示機械振子的平均熱激發(fā)數(shù)；kB為玻爾茲曼常數(shù)；T 為環(huán)境的溫度.

當(dāng)腔場受到強激光驅(qū)動時，對朗之萬方程組（式（2））采用標(biāo)準(zhǔn)的線性化技術(shù)進行處理，將每個海森堡算符重寫為其穩(wěn)態(tài)平均值與微小漲落的和，即O=〈O（t）〉+δO，并通過對腔場進行強激光驅(qū)動使腔內(nèi)光子數(shù)〈a（t）〉滿足〈a（t）〉1.式（2）中，δp1、δp2和δa 為圍繞著穩(wěn)態(tài)平均值的小波動算子，在這種強激光驅(qū)動的情況下，可以安全地忽略非線性項.因此，式（2）可以通過忽略波動中高于一階項的項被線性化.關(guān)于經(jīng)典平均值〈O（t）〉的詳細討論在下面章節(jié)中，同時量子漲落部分δO 的線性化朗之萬方程可以表示為

式（3）中：△1（t）=△0-g〈q1（t）〉-g〈q2（t）〉為由機械運動產(chǎn)生的腔場的有效失諧；式（3）中已經(jīng)忽略掉非線性項[31]，因此系統(tǒng)的有效哈密頓量可以表示為

2 系統(tǒng)的經(jīng)典動力學(xué)及其解析解計算

量子漲落部分（式（3））的演化與經(jīng)典動力學(xué)〈O（t）〉有關(guān)，為研究系統(tǒng)的動力學(xué)演化，首先要求解經(jīng)典平均值.本文中相同頻率的2 個機械振子同時與1 個腔場耦合，因此認為其經(jīng)典動力學(xué)是相同的，即〈q1（t）〉=〈q2（t）〉=〈q（t）〉，〈p1（t）〉=〈p2（t）〉=〈p（t）〉，經(jīng)典平均值的演化可以通過以下非線性微分方程描述

雖然精確求解式（5）中的平均值非常困難，但如果系統(tǒng)遠離光力非穩(wěn)態(tài)和多穩(wěn)態(tài)時，可以用微擾的方式來處理光力耦合[8].在弱光力耦合強度為g 和頻率失諧為Ω 的條件下，將近似解析解展開為雙重冪級數(shù)的形式[32-33]，即

將式（6）代入式（5）可得與時間無關(guān)的系數(shù)On，j（O=p，q，a，j ＝0）

當(dāng)j≥0 時，

圖2 為腔模平均值〈a（t）〉實部和虛部的時間演化關(guān)系及相空間軌跡圖，圖2（a）為通過數(shù)值解（藍色實線）和解析解（紅色虛線）所得腔模平均值〈a（t）〉的實部和虛部隨時間的演化圖像，其中時間單位τ ＝2π/Ω，所選系統(tǒng)參數(shù)為（單位為ωm）κ ＝0.1，Δ0＝1.06，g ＝4×10-6，γm＝10-6，E ＝1.4×104，nm＝0，Λ ＝0.3κ，θ ＝0，Ω ＝2，截斷式（8）到|n|≤1 和j≤8.由圖2（a）可知，在長時極限下，〈a（t）〉的演化周期與調(diào)制周期τ ＝2π/Ω 相同，且解析結(jié)果（紅色虛線）與數(shù)值模擬結(jié)果（藍色實線）非常吻合，說明用微擾的方法求解解析解是可行的.圖2（b）為〈a（t）〉的相空間演化軌跡，其中紅線和藍線分別表示近似解析解和數(shù)值解.數(shù)值解給出的軌跡（藍線）在數(shù)百個調(diào)制周期后收斂為與分析結(jié)果（紅線）一致的極限環(huán).

圖2 腔模平均值〈a（t）〉實部和虛部的時間演化關(guān)系及相空間軌跡圖Fig.2 Time-evolution relations and phase-space trajectories of the real and imaginary parts of the mean value〈a（t）〉of a cavity mould

圖3 為機械模在不同時間間隔內(nèi)的相空間演化軌跡，藍色實線和紅色虛線分別為數(shù)值模擬結(jié)果和解析結(jié)果，所選參數(shù)與圖2 相同.

圖3 不同時間間隔力學(xué)模的經(jīng)典平均值〈q（t）〉和〈p（t）〉的相空間演化軌跡Fig.3 Phase space evolution trajectories of the classical mean〈q（t）〉and〈p（t）〉for the mechanical modes for different time intervals

由圖3 可知，由于γm=κ，經(jīng)典平均〈q（t）〉和〈p（t）〉在相空間中的演化需要260τ～280τ 才能演化到解析結(jié)果所預(yù)測的極限圓.

圖4 為系統(tǒng)達到穩(wěn)定時腔模平均值的模在時間間隔為895τ～900τ 內(nèi)的動力學(xué)演化關(guān)系，所選參數(shù)與圖2 相同.

圖4 系統(tǒng)達到穩(wěn)定時腔模平均值的動力學(xué)演化關(guān)系圖Fig.4 Kinetic evolution of the cavity mode average value when the system reaches stability

圖4 中，〈a（t）〉的解析解（虛線）與數(shù)值解（實線）擬合較好，進一步驗證了微擾近似解析解的準(zhǔn)確性.

3 力學(xué)糾纏與壓縮度量

為在數(shù)值上驗證第2 節(jié)中系統(tǒng)經(jīng)典動力學(xué)的定性討論，本研究通過負對數(shù)值來度量力學(xué)糾纏.首先，引入腔模的振幅和相位漲落算符δX=（δa+δa）?/和δY = （iδa - δa?）/及其相應(yīng)的噪聲算符δXin=則式（3）可以表示為u˙（t）=M（t）u（t）+n（t），其中u（t）T=（δq1，δp1，δq2，δp2，δX，δY），矩陣

式（9）中：n（t）T= [0，ξ（1t），ξ（2t），δXi（nt），δYin（t）]，R1=-κ+2Λcos（Ωt-θ），R2=△-2Λsin（Ωtθ），R3=△-2Λsin（Ωt-θ），R4=-κ-2Λcos（Ωt-θ），G（Xt）和G（Yt）分別為有效耦合G（t）=g〈a（t）〉的實部和虛部.為了確保系統(tǒng)的穩(wěn)定性，Routh-Hurwitz準(zhǔn)則要求M（t）本征值的實部在任何時候都必須小于0[10].后文中所選參數(shù)均已驗證滿足穩(wěn)定性條件，系統(tǒng)最終會趨于一個穩(wěn)定的高斯態(tài).6 × 6 協(xié)方差矩陣V（t）可以描述這個高斯型系統(tǒng)的特性，矩陣元Vi，j=〈ui（t）uj（t）+uj（t）ui（t）〉/2.結(jié)合式（9）有

式（10）中：D=diag[0，-γm（2nm+1），0，-γm（2nm+1），κ，κ]為噪聲關(guān)聯(lián)矩陣.V˙（t）可以描述整個系統(tǒng)的動力學(xué)演化，同時通過數(shù)值模擬可以直接求解式（10）.系統(tǒng)經(jīng)過一段時間的演化后，經(jīng)典動力學(xué)具有一個穩(wěn)定的周期時，可用負對數(shù)值EN度量雙模高斯態(tài)中的兩體糾纏.提取協(xié)方差矩陣V（t）的前四行和前四列，即可組成有關(guān)2 個力學(xué)模式的協(xié)方差矩陣

式（11）中：A、B 和C 分別為2×2 的子矩陣，負對數(shù)值

式（12）中

式（13）中：Σ（V）=detA+detB-2detC，如EN>0，即η<1/2，說明2 個力學(xué)振子間存在糾纏.

協(xié)方差矩陣V（t）的第1 個對角矩陣元V11（t）=〈δq（t）2〉和第2 個對角矩陣元V22（t）=〈δp（t）2〉分別表示力學(xué)振子的位移和動量漲落的方差.系統(tǒng)達到穩(wěn)定時，如滿足〈δq（t）2〉<1/2 或〈δp（t）2〉>1/2，則對應(yīng)的坐標(biāo)或動量分量被壓縮.力學(xué)壓縮的強度可用dB 為單位來度量，對應(yīng)的計算方式為-log10[〈δO（t）2〉/〈δO（t）2〉vac]（O=p 或q）和〈δq（t）2〉vac=〈δp（t）2〉vac=1/2 分別表示力學(xué)模真空態(tài)的位移和動量方差.

4 結(jié)果與討論

4.1 機械糾纏

通過對負對數(shù)值EN進行數(shù)值模擬，分析OPA 對機械糾纏的影響.首先，給出OPA 的相位對機械糾纏EN的影響.圖5 為不同相位時，EN隨時間t 的變化圖像.圖5 中，E ＝6×104，其他參數(shù)與圖2 相同.由圖5可以看出，系統(tǒng)經(jīng)過一段時間的演化后，機械糾纏與經(jīng)典動力學(xué)一樣最終以周期τ 隨時間變化.因此，下文只考慮相位θ ＝0 的情況.

圖5 力學(xué)糾纏EN 在不同的參量相位下隨時間t 的演化關(guān)系Fig.5 Evolution of mechanical entanglement EN with time t for different parametric phases

由于機械糾纏的演化具有周期性，可以通過一個周期內(nèi)EN的最大值來量化機械糾纏的大小[34].即

圖6 為機械糾纏的最大值EN，max隨OPA 失諧量Ω/ωm的變化關(guān)系，圖6 中最佳失諧Ωopt/ωm＝2.008，其他參數(shù)與圖5 相同.

圖6 最大機械糾纏EN，max 隨OPA 失諧量Ω/ωm 的變化關(guān)系Fig.6 Variation of maximum mechanical entanglement EN，max with OPA detuning Ω/ωm

由圖6 可以看出，存在最優(yōu)的調(diào)制頻率Ωopt/ωm＝2.008 使EN，max最大，且由于光力耦合對光腔有效失諧△（t）的輕微修正，最優(yōu)調(diào)制頻率Ωopt接近但略大于2ωm，這正是前文討論中選取Ω ＝2ωm的原因.

為研究有限熱溫度和OPA 對機械糾纏的影響，圖7 為不同熱聲子數(shù)條件下以及OPA 的增益Λ 在有限溫度下機械糾纏隨時間的演化關(guān)系圖，圖7 中參數(shù)與圖5 相同.圖7（a）為不同熱聲子數(shù)nm＝0（藍色）和nm＝0.2（紅色）條件下機械糾纏隨時間的演化.圖7（b）為OPA 的增益Λ ＝0（藍色）和Λ ＝0.3κ（紅色）對有限溫度下機械糾纏演化的影響.

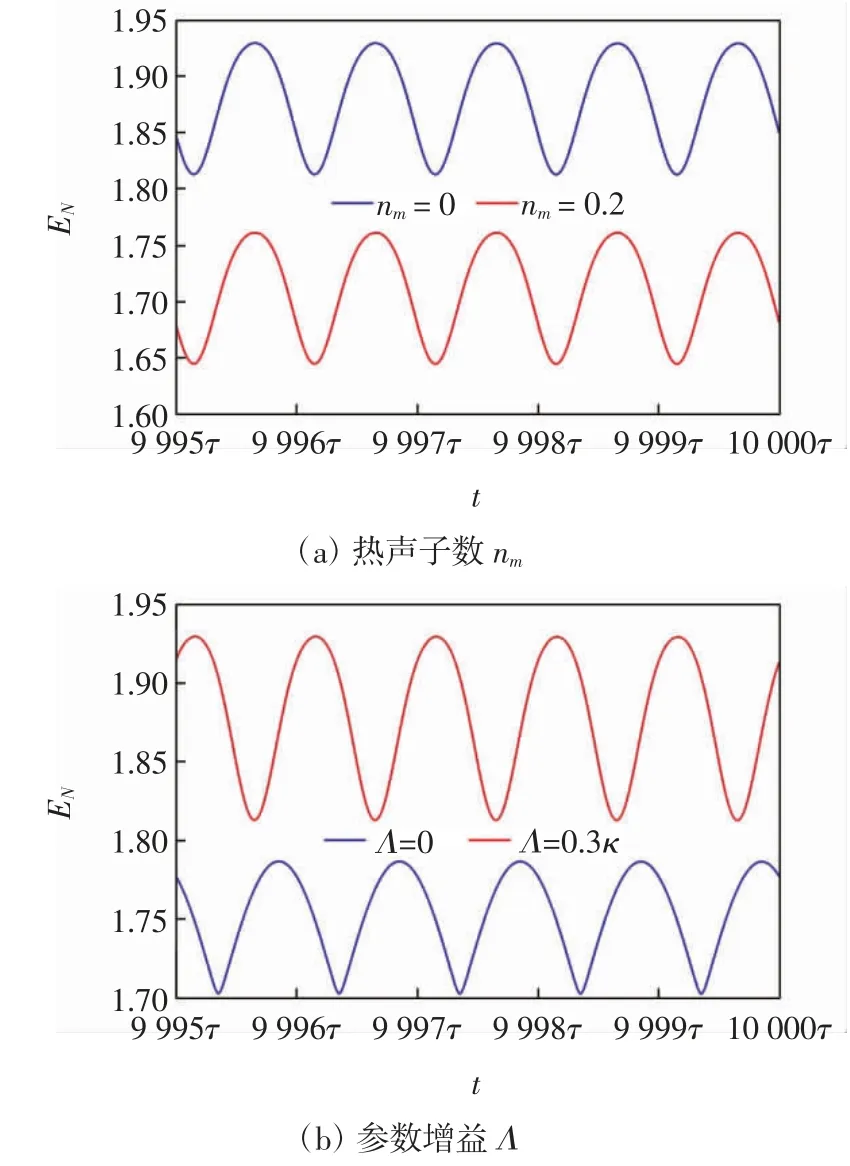
圖7 系統(tǒng)達到穩(wěn)定時機械糾纏EN 隨時間的演化關(guān)系Fig.7 Evolution of mechanical entanglement EN with time as the system reaches stability

由圖7（a）可以看出，隨著熱聲子數(shù)的增加，環(huán)境溫度的升高抑制了系統(tǒng)的量子效應(yīng)，導(dǎo)致系統(tǒng)機械糾纏的值降低.由圖7（b）可以看出，與Λ ＝0 的情況相比較，隨著Λ 的增大，機械糾纏被增強，這表明在OPA 的輔助下機械糾纏可以在一個相對較大的熱聲子數(shù)條件下存在，即機械糾纏對熱噪聲具有很強的魯棒性.

4.2 壓縮效應(yīng)

最后，通過計算動量漲落的方差〈δp2〉研究調(diào)制OPA 對機械壓縮的影響.根據(jù)海森堡測不準(zhǔn)原理，當(dāng)〈δp2〉<1/2 時，機械振子的動量獲得壓縮.圖8 為OPA的增益Λ 取不同值時，〈δp2〉隨時間的變化，圖8 中其他參數(shù)與圖5 相同.

圖8 力學(xué)漲落的方差〈δp2〉隨時間的變化關(guān)系Fig.8 Variance of the force rise and fall〈δp2〉versus time

由圖8 可知，相比于Λ=0 的情況，隨著Λ 的增大，機械振子的動量壓縮被周期性加強.當(dāng)Λ=0.8κ 時，〈δp2〉最小值達到7.12 dB（對應(yīng)的動量方差〈δp2〉min=0.097 41），遠大于一般的機械壓縮，可以認為是強壓縮[35-37]，這說明機械壓縮可以在調(diào)制OPA 的輔助下增強.

圖9 為熱聲子數(shù)nm對機械壓縮的影響，圖9 中其他參數(shù)與圖5 相同.

圖9 力學(xué)漲落的方差〈δp2〉隨時間的變化關(guān)系Fig.9 Varianceofthemechanicalriseandfall〈δp2〉versustime

由圖9 可以看出，〈δp2〉的最小值隨熱聲子數(shù)nm的增加略有增加，即使nm增大到500，仍可實現(xiàn)機械壓縮，因此系統(tǒng)產(chǎn)生的機械壓縮對環(huán)境溫度具有很強的魯棒性.

以上討論的機械壓縮是在邊帶可分辨的條件下，即ωm?κ.而標(biāo)準(zhǔn)的腔光力系統(tǒng)很難在實驗中獲得高品質(zhì)的腔，并滿足可分辨邊帶條件，因此討論在邊帶不可分辨條件（κ>ωm）下是否可以實現(xiàn)機械壓縮非常必要.

圖10 給出邊帶不可分辨條件（κ>ωm）下，力學(xué)漲落的方差〈δp2〉隨時間的變化關(guān)系，圖10 中其他參數(shù)與圖5 相同.

圖10 邊帶不可分辨條件（κ>ωm）下力學(xué)漲落的方差〈δp2〉隨時間的變化關(guān)系Fig.10 Variance of mechanical rise and fall〈δp2〉versus time under indistinguishable conditions（κ>ωm）in the sidebands

由圖10 可以看出，機械壓縮的程度隨著腔耗散率κ 的增加明顯減弱，但仍可以在邊帶不可分辨條件（κ>ωm）下實現(xiàn)機械壓縮.因此，在調(diào)制OPA 的輔助下，對于耗散較大（κ>ωm）的光力系統(tǒng)也可以實現(xiàn)機械壓縮.

5 結(jié)論

本文研究了與同一光腔耦合的2 個機械振子間的量子糾纏和機械壓縮.通過數(shù)值和解析求解經(jīng)典平均值的運動方程，分析了系統(tǒng)動力學(xué)的演化.計算結(jié)果表明，調(diào)制光學(xué)參量放大器對雙機械振子腔光力系統(tǒng)中的量子糾纏和機械壓縮效應(yīng)的影響均有良好的效果：

（1）對系統(tǒng)施加調(diào)制OPA，通過調(diào)節(jié)OPA 相對于驅(qū)動激光的失諧量可以增強2 個機械振子間的糾纏.

（2）在調(diào)制OPA 的輔助下，機械振子間的糾纏對系統(tǒng)的熱噪聲表現(xiàn)出很強的魯棒性.

（3）在邊帶可分辨條件下，通過調(diào)制OPA 的作用可以實現(xiàn)較強的機械壓縮，且對于邊帶不可分辨的情況，利用調(diào)制OPA 也可產(chǎn)生機械壓縮.因此調(diào)制OPA對于系統(tǒng)實現(xiàn)機械壓縮具有關(guān)鍵的作用.