混合半徑高斯濾波算法在去除GRACE條帶誤差中的應用

付 林 趙東明 付林威

1 信息工程大學地理空間信息學院,鄭州市科學大道62號,450001

重力場是地球的基本物理場,通過確定地球重力場及其變化可以反映出地球內部質量分布以及地表物質遷移情況[1]。GRACE(gravity recovery and climate experiment)重力衛星為監測大尺度地球重力場變化、恢復地球重力場提供支持,它的出現解決了人們無法持續有效觀測地球重力場這一難題,為地球科學研究作出重要貢獻[2]。

由于GRACE采用南、北雙星跟蹤飛行模式,導致其觀測信息也是呈南北條形分布, GRACE獲得的地球時變重力場信息會出現嚴重的南北條帶誤差,這在很大程度上掩蓋了真實重力信號[3]。目前,國內外學者處理條帶誤差的主要手段分為兩大類:一是通過降低含有噪聲的高階項權重來降低噪聲,比如高斯濾波等,該類方法雖然可以較好地濾除噪聲,但由于是通過降低高階權重實現的,不可避免地會損失掉一些真實高頻信號,而且隨著濾波半徑的增大,信號損失會更嚴重;二是通過濾除重力場球諧系數奇偶項之間的相關性而達到濾除噪聲的目的[4],如去相關濾波[5]等,此類方法對濾波造成的信號損失較小,但對于低緯度地區的濾波效果較差,仍會存在條帶誤差。因此,為實現最大程度地保留真實信號并且擁有較好的濾波效果,人們通常采用去相關與高斯濾波相結合的組合濾波方法。同時,在GRACE運行期間存在部分月份數據缺失,對此常用三次樣條插值法對短期缺失數據進行填補。而對于GRACE與GRACE-FO兩代衛星之間11個月的數據空白,莫紹興等[6]提出利用貝葉斯卷積神經網絡提取時變重力場信號有效特征,從而對缺失數據進行預測;也有專家提出利用奇異譜分析法[7]恢復兩代衛星間的缺失值,均取得較好效果。

1 濾波處理方法

利用GRACE時變重力場反演地球表面質量變化,在大尺度范圍內,我們通常近似認為地表質量變化所引起的時變重力場變化實際就是地面水質量的變化。因而通過地表質量變化模型再除以水的密度便可以得到陸地等效水高,進而計算陸地水儲量變化[8]:

(1)

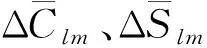
1.1 Gaussian濾波方法

Wahr等[8]提出一種基于平滑函數的高斯濾波方法,并推導了一組高斯平滑濾波系數,應用于GRACE數據處理中。高斯濾波削弱條帶誤差的主要原理就是通過降低球諧系數高階項的權重,將高階項中存在的條帶誤差信號濾除掉。其高斯平滑核函數定義為:

(2)

式中,α為球面兩點夾角,r為濾波半徑。給出高斯濾波的遞推系數:

(3)

Chambers等[9]研究發現,當以上高斯濾波算法在球諧系數高于50階時存在不確定性,因此提出高斯濾波改進算法。改進算法的平滑函數如下:

(4)

1.2 去相關濾波

Swenson和Wahr[10]研究發現,GRACE條帶誤差存在的一個重要原因就是其時變重力場球諧系數奇偶項之間存在明顯的相關性,因此國內外專家學者提出利用多項式擬合來去除相關性的去相關濾波方法,其基本原理就是對球諧系數項的奇、偶數階分別進行滑動固定窗口的多項式擬合,擬合值認為是存在的相關誤差,將原始球諧系數減去擬合值即為去相關濾波后的球諧系數。

Chen等[11]根據上述基本思想進行改進,提出PnMl方法。該方法原理主要為:對系數的前l階位系數不作處理,對大于等于l階的位系數用n階多項式進行奇偶項擬合并扣除相關值。

不同品種的茼蒿葉片中葉綠素a、b含量、總葉綠素含量及SPAD值都不相同，對SPAD值及葉綠素含量間的相互關系進行統計分析，發現SPAD值與葉綠素含量均呈顯著正相關性，與水稻、小麥、草莓、園林樹木、烤煙、無花果等的研究結果相似[12-14]。而“小葉茼蒿”的4種數學模型的相關系數均達到0.6以上，葉綠素a含量與SPAD值的最優函數模型是指數方程，葉綠素b與SPAD值的最優函數模型是對數函數，而總葉綠素含量與SPAD值的最優函數模型則是線性方程。“大葉茼蒿”的4種數學模型的相關系數普遍較低，由此可推斷“大葉茼蒿”的SPAD值與葉綠素含量相關性較差。

同時研究發現,GRACE時變重力場模型的球諧系數精度與階次數密切相關,低階次系數間的相關誤差小,但球諧系數的標準差隨著階數和次數的增大而增大。Duan等[12]在Swenson等[10]提出的滑動固定窗口多項式擬合去相關濾波的基礎上,建立滑動可變窗口多項式擬合去相關濾波方法。

1.3 組合濾波方法

隨著高斯濾波半徑的增大,對條帶誤差的濾除效果越好,但由于高斯平滑濾波是通過降低高階項的權重系數來壓制噪聲,因此會不可避免地濾除掉高階項真實信號。去相關濾波也可在一定程度上去除條帶誤差,但在中緯度地區仍存在噪聲信息。因而,為在濾除條帶噪聲的同時盡量保留真實信號,國內外學者發現組合濾波方法,即去相關濾波與高斯濾波相結合的方法可以最大程度地壓制噪聲并保留真實信號[4]。

1.4 信噪比估計

目前對各種濾波效果的評估國內外尚未有統一標準,通常采用的是通過分析濾波前后誤差的RMS(root-mean-square)以及陸地與海洋信噪比(signal-to-noise ratio,SNR)方法。經研究,GRACE測量誤差在陸地與海洋上大致處于同一水平,而陸地質量變化信號強于海洋,因此Chen等[11]根據此原理構建出一套基于陸地海洋信噪比最大為準則的濾波器,其信噪比公式為:

(5)

式中,MASSland為陸地質量變化,MASSocean為海洋質量變化,Err為GRACE測量誤差。

2 實驗分析

2.1 數據預處理

本文采用得克薩斯空間研究中心(Center for Space Research, CSR)的GRACE RL06月重力場模型,模型截斷階數為60,選取2004-01～2010-12數據作為研究對象,該范圍內GRACE衛星運行正常,數據質量較好,且不存在數據空白月份。

由于GRACE衛星對代表地心運動的一階項不敏感,導致一階項缺失,這里采用Swenson等[10]計算的一階項進行補充。受GRACE衛星運行軌道因素影響,其解算的C20項存在較大不確定性,利用衛星激光測距(SLR)獲取的C20項對其進行替換。為體現出重力場時變信息,這里選取所有月份球諧系數平均值作為背景重力場,將每月的球諧系數減去該背景重力場,得到各月時變重力場球諧系數。

2.2 高斯濾波信噪比分析

郭飛宵等[3]指出,時變重力場模型低于20階的項主要反映地幔以下的重力場信號,20～30階項體現信號與噪聲混合信息,而高于30階項則包含更多的噪聲信息。由表1可見,高斯濾波半徑為0 km(即對條帶誤差不進行處理)時,隨著階數的不斷增大,信噪比不斷變小,在球諧系數大于30階時信噪比減小較快,至60階時降低為1.252。這也證實高階項以噪聲為主,對真實信號掩蓋嚴重,造成信噪比急劇減小。隨著高斯濾波方法的加入,GRACE球諧系數中的噪聲誤差被減弱,信噪比有較明顯提升,從不同階下的信噪比情況也可以看出,當高斯濾波半徑為400 km時,其信噪比在各階均處于最優水平,因此在僅用高斯濾波去除條帶誤差時,常選取400 km半徑的高斯濾波作為最優濾波半徑。

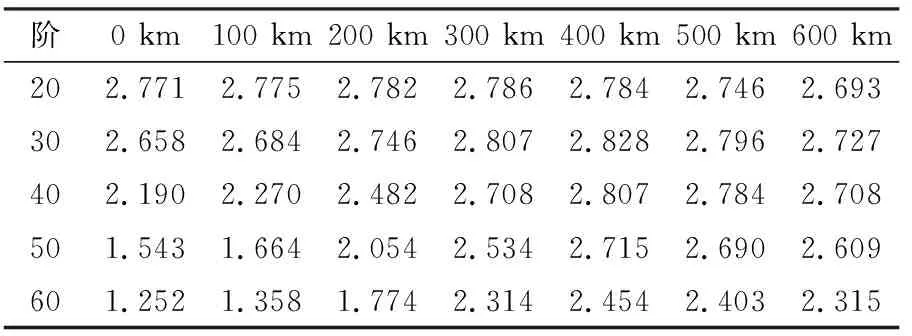
表1 各階數下不同濾波半徑的高斯濾波信噪比

2.3 組合濾波信噪比分析

研究發現,GRACE球諧系數奇偶項之間具有相關性,因此認為GRACE球諧系數誤差中存在相關性誤差。為有效去除GRACE存在的誤差,目前常采用組合濾波的方法,即去相關濾波+高斯濾波方法,可以最大程度地減弱條帶誤差項。這里選取Duan等[12]提出的去相關濾波與高斯濾波結合的組合濾波方法,不同階數以及高斯濾波半徑下的信噪比如表2所示。可以看出,在不進行高斯濾波的情況下,經去相關濾波后的時變重力場信噪比有明顯提升,這也印證了相關性誤差確實存在于時變重力場球諧系數中。同時,分析去相關濾波后不同半徑下的高斯濾波信噪比也可以看出,由于去相關濾波減弱了相關性誤差,因此在300 km高斯濾波半徑下其信噪比在各階下均處于最優水平。

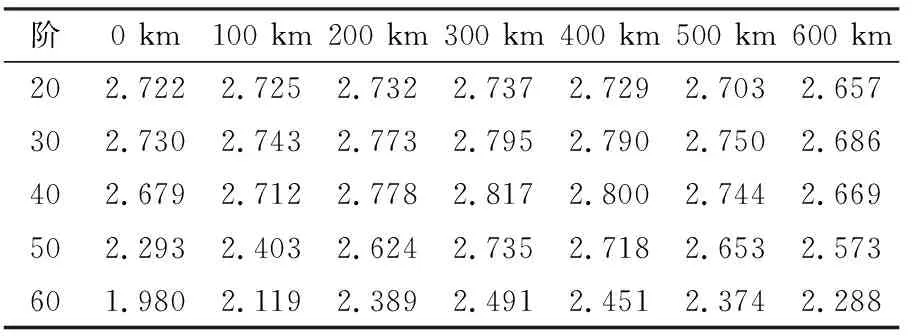
表2 各階數下不同濾波半徑的組合濾波信噪比

2.4 混合半徑高斯濾波算法

不同半徑下的高斯濾波權重系數如圖1所示,可以看出,隨著濾波半徑的增大,高階項的權重系數下降得越來越快。雖然壓制了高階項噪聲,但由于權重系數下降過快,也會導致信號損失過多,尤其在含誤差較少的低階項部分,由于濾波半徑增大,權重系數減小較快會導致真實低頻信號損失。

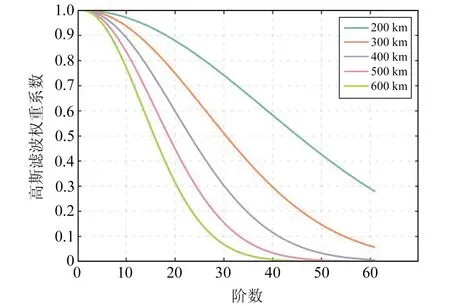
圖1 不同濾波半徑高斯權重系數Fig.1 Gaussian weight coefficients with different filtering radius

分析表1可知,當球諧系數階數較低(如20階)時,里面所包含的噪聲信息較少,不同高斯濾波半徑與原始球諧系數相比信噪比變化較小,且隨著濾波半徑的增大,權重系數下降快,會造成真實信號較快損失。為應對這種情況,本文提出一種混合半徑的高斯濾波方法,即通過調整球諧系數不同階次項的高斯權重系數進行分段高斯濾波,實現在盡可能濾除高頻誤差的同時盡量多地保留低頻信息。

首先確定階數L、濾波半徑R和分段步數S,則可以將階數和高斯濾波半徑按下式劃分:

(6)

式中,r0為原始濾波半徑按步長劃分的濾波半徑段長,l0為給定球諧階數按步長劃分后每段階數大小,ri、li分別為第i段對應的高斯濾波半徑以及所取的部分階數。

根據式(4)給出的不同階數半徑下的改進高斯濾波權重系數Wl,可計算出每段高斯濾波半徑對應的濾波半徑下高斯權重系數:

(7)

提取不同階數范圍的高斯權重系數并進行重組,便可得到拼接后的高斯濾波權重系數。由于不同階數對應濾波系數不同,為保證高斯濾波的平穩性,還要對組合拼接的濾波系數進行移動平均平滑處理,最終得到改進的高斯濾波權重系數:

(8)

根據表1及表2可得出結論,只進行高斯濾波情況下,400 km高斯濾波的信噪比最優,進行組合濾波時,Duan等[12]與300 km半徑高斯濾波信噪比最優。混合半徑高斯濾波方法的目的就是在相同濾波半徑下盡可能保留信號、提升信噪比。利用式(8)改進的高斯濾波方法進行信噪比分析(表3),可以看出,當僅用一步進行分段高斯濾波時,分段高斯濾波即為經典高斯濾波;在僅進行混合半徑高斯濾波的情況下,400 km濾波半徑分兩步進行濾波信噪比最大;在進行組合濾波時,分3步進行的300 km混合半徑高斯濾波信噪比最大。

表3 混合半徑高斯濾波信噪比

為進一步驗證該方法能否更好地保留真實信號,本文對不同濾波半徑的傳統高斯濾波、傳統組合濾波以及混合半徑高斯濾波、去相關濾波[12]與混合半徑高斯濾波的改進組合濾波方法的信噪比進行對比,結果如圖2所示。可以看出,混合半徑高斯濾波方法在不同濾波半徑下信噪比均處于較優水平。此外,隨著傳統高斯濾波半徑的增大,因濾波造成的信號損失也越嚴重,而利用本文的混合半徑高斯濾波方法對信號保留效果較好。

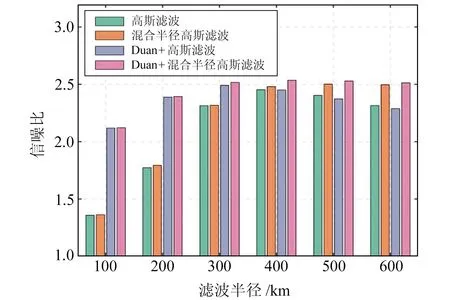
圖2 不同濾波方法信噪比Fig.2 SNR of different filtering methods

圖3展示了利用GRACE反演全球陸地水儲量變化的效果,可以看出,不進行濾波或只進行去相關濾波都無法完全提取真實的等效水高信號,而經過經典高斯濾波、經典組合濾波以及混合半徑高斯濾波、Duan等[12]與混合半徑高斯濾波的改進組合濾波均對條帶噪聲有明顯壓制作用,真實等效水高信號已經顯現。

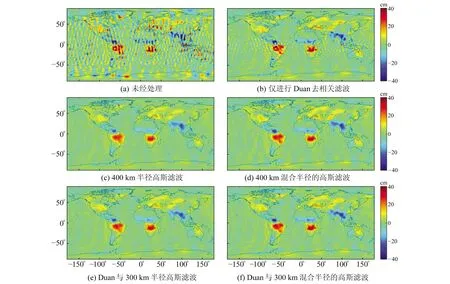
圖3 全球陸地水儲量變化Fig.3 Changes in global land water reserves

同時,對比分析圖3中高斯濾波(c)和混合半徑高斯濾波(d)、組合濾波(e)和Duan等[12]與混合半徑高斯濾波的改進組合濾波(f)兩組全球陸地水儲量變化中水儲量信號變化較劇烈的亞馬遜流域、剛果盆地地區的等效水高信號可以看出,經典高斯濾波方法對信號平滑效果更強,尤其在剛果盆地地區最為明顯,而對信號過度平滑則會造成區域信號泄漏。相比之下,混合半徑高斯濾波在保證去條帶誤差的同時還能較好地減弱信號泄漏,提高區域反演結果的準確性,這也再次印證改進高斯濾波能更好地保留水儲量變化信號的判斷,證明改進高斯濾波具有可行性。

3 結 語

本文對GRACE時變重力場條帶誤差的處理方法進行分析,著重討論時變重力場球諧系數不同階數下不同半徑的高斯濾波以及組合濾波的信噪比情況。結果表明,在低于20階時,球諧系數具有較高信噪比,因此不同半徑高斯濾波效果近似;當球諧系數大于30階時信噪比較低,因此需要用濾波手段提高信噪比。

通過不同高斯濾波半徑下的經典高斯濾波以及組合濾波信噪比的分析可以發現,僅進行高斯濾波時,400 km半徑高斯濾波信噪比最優,在各階下處于最好水平;在進行Duan等[12]去相關濾波和高斯濾波組合濾波時,由于消除了球諧系數的相關性誤差,因此在進行300 km半徑高斯濾波時,球諧系數各階下信噪比處于最好水平。

對得到的最優高斯濾波半徑進行改進,結果表明,僅進行經典高斯濾波時,分兩步進行的400 km混合半徑的高斯濾波信噪比較經典高斯濾波更優;進行組合濾波時,Duan等[12]與分3步進行的300 km混合半徑高斯濾波信噪比更優。對全球陸地水儲量變化較為劇烈的亞馬遜流域、剛果盆地地區信號分析可以看出,混合半徑高斯濾波能更好地保留真實信號,減弱因高斯平滑造成的區域信號泄漏。