優化數學認知結構 提升一輪復習效率
——以“函數零點”復習課為例

福建省浦城縣第二中學 (353400) 黃慧美

一輪復習是高考復習教學的關鍵一環.在此階段,學生依然是課堂的主體,然大多復習課堂卻以教師為主導,延續著“師講生聽”的教學模式,課堂容量大、頻率快,容易出現學生“懂而不會”的尷尬局面.實際上,一輪復習要重視通性通法的提煉,讓解題方法和解題策略更具系統性和方向性,使復習更高效,解題更流暢.本文筆者以“函數零點”復習為例,以典型問題為切入點,引導學生在鞏固基礎知識的同時,掌握解題通法,構建數學思想方法體系,進而優化認知結構,提升復習效率.

一、教學實錄

1.明確方向,激發欲望

A.(0,1) B.(1,2) C.(2,4) D.(4,+∞)

在復習階段,不能將目光定位在解題上,而是要透過題目了解考試動向,分析核心考點,進而進一步鞏固“雙基”,掃清解題障礙.

師:題中涉及到什么概念?

生齊聲答:函數的零點.

師:函數零點的概念大家還記得嗎?

生1:使函數f(x)=0成立的實數x叫函數y=f(x)的零點.

師:很好,那么想一想例1該如何求解呢?

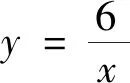
生3:生2的解法沒有問題,解題時既要畫圖又要代值,我覺得這個問題可以換個思路來解,可以考慮應用零點存在的定理來解答.

師:說說你的解題思路.

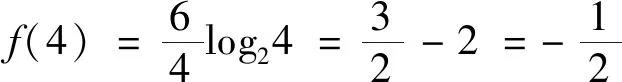
師:很好,通過代數法和幾何法都順利地得到了答案.生2是從定義的角度去考慮,首先將函數零點問題轉化為方程的根,然本題方程難以直接求解,為此又繼續轉化,將其轉化為函數的交點問題,最后利用數形結合的思路精準地求得了答案,這是解決此類問題的一個常……