Python在曲線平移可視化中的應用研究
張朋 賈棟梁 咸慶軍 崔偉華 曾長女

DOI:10.19850/j.cnki.2096-4706.2024.02.039
收稿日期:2023-05-08
基金項目:河南工業大學本科教育教學改革研究與實踐項目(2023GJYJTM16);河南省新工科研究與實踐項目(2020JGLX039);河南省高等教育學會高等教育研究項目(2021SXHLX145);河南省高等教育教學改革研究與實踐重點項目(2021SJGLX144)
摘? 要:平移運動是理論力學的一項重要內容,曲線平移是平移運動中的難點內容,其抽象枯燥。采用圖形和動畫等可視化教學手段,可以化抽象為具體,從而降低理解難度。編制曲線平移動畫程序,提供了深入理解曲線平移的另一種方式,可以提升學習效果,也提供了一個編程實踐的機會。該文詳細介紹了利用Python制作曲線平移動畫程序,加深了學生對利用Python繪制圖形和制作動畫的理解,豐富了學生的信息技術知識,也加深了學生對平移運動的理解,進一步增強了學生對理論力學課程的興趣和信心。
關鍵詞:理論力學;曲線平移;可視化
中圖分類號:TP39;G434 文獻標識碼:A 文章編號:2096-4706(2024)02-0182-05
Research on the Application of Python in Curve Translation Visualization
ZHANG Peng, JIA Dongliang, XIAN Qingjun, CUI Weihua, ZENG Zhangnyu
(College of Civil Engineering, Henan University of Technology, Zhengzhou? 450001, China)
Abstract: Translation motion is an important content of theoretical mechanics. Curve translation is a difficult content in translation motion, which is abstract and boring. The use of visual teaching tools such as graphic and animation can reduce the difficulty of understanding by turning the abstract into the concrete. Developing curve translation animation program provides an alternative way of gaining insight into curve translation, can improve learning effect, and also provide an opportunity for programming practice. The curve translation animation creating program using Python is introduced in detail in this paper, which deepens students' understanding of drawing graphics and creating animations using Python, enriches their knowledge of information technology, deepens their understanding of translation motion, and further enhances their interest and confidence in the theoretical mechanics course.
Keywords: theoretical mechanics; curve translation; visualization
0? 引? 言
理論力學是土木工程、機械工程等專業的專業基礎課程[1],是必須掌握的理論課。理論力學包含三大部分:靜力學、運動學和動力學。運動學只從幾何角度研究物體的運動,其是機構運動分析的基礎,并且是動力學部分的基礎,因此非常重要。剛體的平移運動是運動學中的基礎內容,是運動學后續重難點內容(點的合成運動、剛體的平面運動)的基礎,因此平移運動是理論力學課程的一項重要內容。平移運動包括直線平移和曲線平移,直線平移較簡單,曲線平移是平移運動中的難點內容。然而教材只是通過簡單的理論推導與敘述來介紹此部分內容,比較抽象枯燥。若采用傳統教學手段,學生此部分內容的學習效果則不太理想。隨著信息技術的快速發展,教育工作者采用圖形動畫等可視化教學手段,將抽象概括的知識以視覺表征的方式呈現給學生,化抽象為具體、變靜態為動態,從而降低知識的理解難度,加深學生的理解,最終提升學習效果[2,3]。提升學生的計算機應用能力和編程水平也是當代教育的一項重要內容,但多數學生的編程只是囿于計算機編程課和計算機等級考試[4],缺乏解決實際問題的編程鍛煉。編制一個制作曲線平移動畫的程序,則提供了一個編程實踐的機會,并且可以深入理解和掌握曲線平移。
不少學者采用MATLAB、Maple等國外商業軟件進行了運動學教學研究[5-9],然而這些商業軟件往往價格昂貴,多數單位及個人難以負擔,且其中某些軟件已經禁止我國部分高校和單位使用。開源免費的Python則不存在這些問題,而且Python提供了非常完善的基礎代碼庫,從而使得Python既適用于傳統的Web開發、PC軟件開發等,也適用于當下熱門的機器學習、大數據分析等,因而Python成為現在最熱門的編程語言之一。已有學者利用Python進行了理論力學相關的教學研究[10],但還不多見,尤其在運動學方面。本文將圍繞曲線平移這一知識點,系統地介紹如何利用Python編制曲線平移動畫程序。
1? Python基礎知識
Python是一種解釋型、面向對象、動態數據類型的高級程序設計語言,其與其他語言有許多相似之處,但也存在一些差異。Python提供了眾多的基礎代碼庫,可以使用Matplotlib繪制圖形和制作動畫。
1.1? Python基本語法
Python最具特色的就是用縮進來寫模塊,縮進的空白數量是可變的,但是所有代碼塊語句必須包含相同的縮進空白數量。Python中的標識符(作為變量、函數、類、模塊以及其他對象的名稱)由字母、數字、下劃線組成,區分大小寫,一般以字母開頭。
Python有五個標準的數據類型:Numbers(數字)、String(字符串)、List(列表)、Tuple(元組)、Dictionary(字典)。其中,Python的列表是用方括號([])標注,逗號分隔的一組值。列表是Python中使用最頻繁的數據類型,可以完成大多數集合類的數據結構實現。它支持字符、數字、字符串甚至可以包含列表(即嵌套)。使用“append()”方法向列表添加項。
Python常使用for循環。Python的for語句迭代列表或字符串等任意序列,元素的迭代順序與在序列中出現的順序一致。內置“range()”函數常用于遍歷數字序列,該函數可以生成算術級數,生成的序列不包含給定的終止數值。
1.2? Matplotlib
Matplotlib是一款用于數據可視化的Python庫,支持跨平臺運行,能夠輕松地實現各種圖形的繪制。Pyplot是Matplotlib的子庫,提供了和MATLAB類似的繪圖API,能方便地繪制2D圖表,使用前需要使用“import matplotlib.pyplot as plt”引入。Animation是Matplotlib的另一子庫,可以繪制復雜動畫并能生成gif動畫文件,使用前需要使用“import matplotlib.animation as animation”引入。Matplotlib生成的圖形主要由包括:Figure(整個圖形畫布)和Axes(繪圖區域)。示例代碼如下:
fig =plt.Figure(dpi=100)
plt.gcf().set_size_inches(20, 10)
fig.tight_layout()
ax = fig.add_subplot(1,1,1)
此段代碼在創建了一個寬為20、高為10的Matplotlib空白圖形,之后可以在繪圖區域繪制圖形。
Pyplot使用“plot()”函數繪制點和線,其具有可選格式的字符串參數,用來指定線型、標記顏色、樣式以及大小。使用“text()”函數向繪圖區域添加文本。Matplotlib可以根據自變量與因變量的取值范圍,自動設置x軸與y軸的數值大小,也可以使用“set_xlim()”和“set_ylim()”對x、y軸的數值范圍進行設置。
運動學中的桿件可以使用“plot()”函數繪制兩條不同寬度不同顏色的線條組合來表示,鉸連接可以使用“plot()”函數繪制兩個不同大小不同顏色的點組合來表示。
Animation使用“FuncAnimation(fig, func, frames, init_func, interval)”函數制作動畫,fig為繪制動畫的畫布名稱;func為繪制每幀動畫的函數,其第一個參數為幀序號;frames為動畫幀序號組成的列表,其值會傳遞給func函數;init_func為繪制動畫前的初始化函數;interval為幀之間的間隔時間,單位為毫秒。使用“save(filename)”函數將繪制的動畫保存為gif動圖或視頻。
2? 曲線平移基本理論
如果在剛體內任取一直線段,在運動過程中這條直線段始終與它的最初位置平行,這種運動稱為平行移動(平移運動[11]),簡稱平移[1]。當剛體平行移動時,其上各點的運動相同,軌跡形狀相同;在每一瞬時,各點的速度相同,加速度也相同。
平移包括直線平移和曲線平移[1,11]:平移剛體上的點做直線運動,則為直線平移;平移剛體上的點做曲線運動,則為曲線平移。曲線平移具有平移運動的上述特點。文獻[1]中例7-9和習題7-18中的鉸接四邊形機構(機械工程中稱為平行四邊形機構[12])的水平桿作曲線平移。
本文新建一平行四邊形機構,其包括曲柄OC、曲柄O1C1和水平連桿CC1,OC=O1C1=r,CC1=OO1=L,連桿CC1做曲線平移,曲柄OC以勻角速度ω轉動,初時刻時曲柄OC與水平線間的夾角為φ0。以O為坐標原點,則點O1坐標為(L,0)。
點C的運動方程為:
點C1的運動方程為:
3? 曲線平移可視化的Python實現
本節將詳細介紹利用Python編制曲線平移可視化程序。
3.1? 平行四邊形機構數據計算與存儲
賦予變量具體數值,計算第i幀對應的時刻t,根據關鍵點的運動方程,計算此時平行四邊形機構中各關鍵點的坐標,分別存儲在變量“x_C”“y_C”“x_C1”“y_C1”中,Python代碼如下:
t=i*0.02
L,r =560,200
w=1
phi0=math.pi/4
x_O,y_O=0,0
x_O1=L
y_O1=0
phi=w*t+phi0
x_C=r*math.cos(phi)
y_C=r*math.sin(phi)
x_C1=x_C+L
y_C1=y_C
3.2? 平行四邊形機構繪制
繪制開始時需先清除繪圖區域并進行尺寸等設置。Python代碼如下:
ax.cla()
ax.axis('equal')
ax.set_xlim(-210,800)
ax.set_ylim(-255,255)
ax.axis('off')
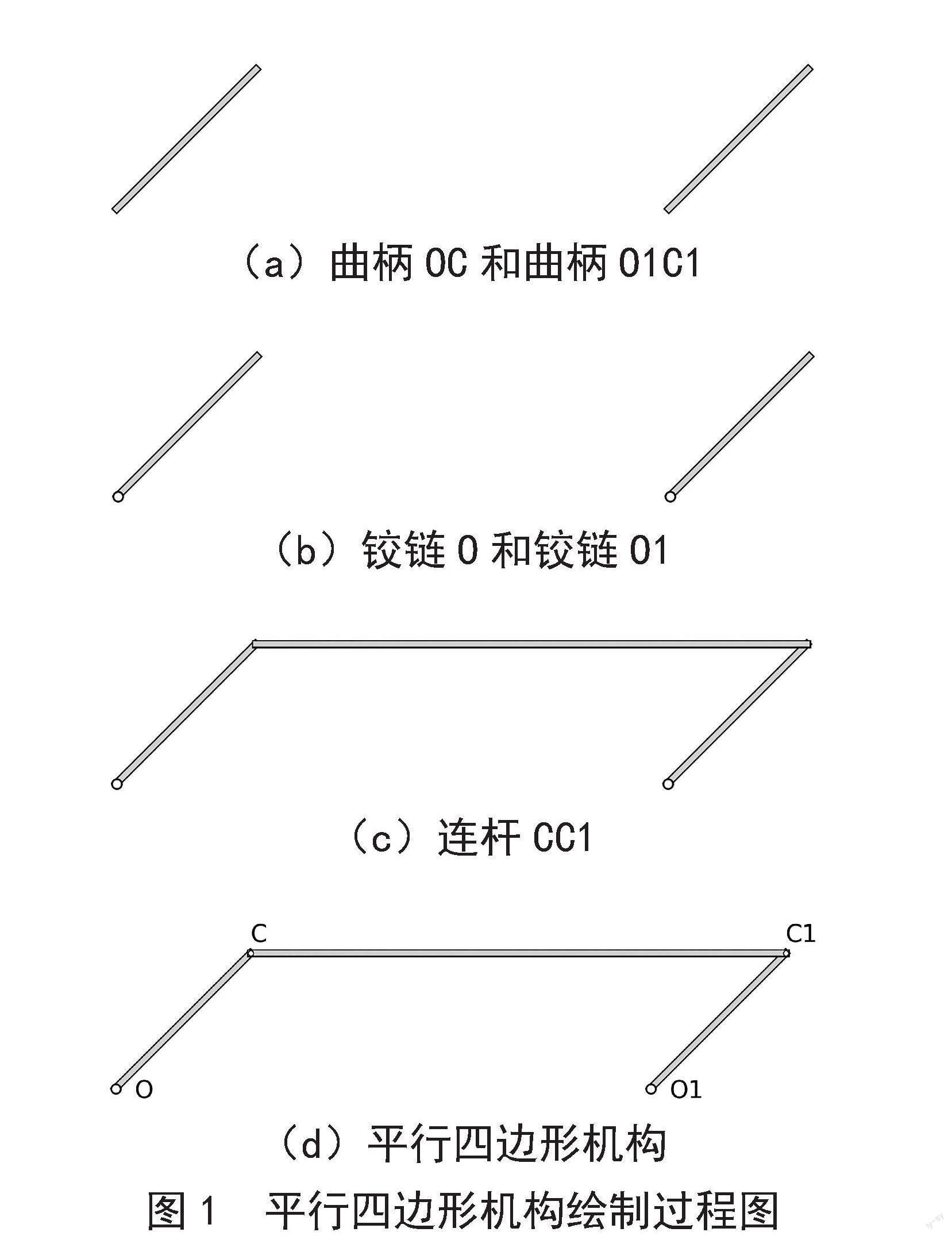
根據關鍵點O、C、O1、C1的坐標,依次繪制曲柄OC、曲柄O1C1,初時刻時繪制結果如圖1(a)所示。Python代碼如下:
ax.plot([x_O,x_C],[y_O,y_C],linewidth =9.0,color='k')
ax.plot([x_O,x_C],[y_O,y_C],linewidth =6.0,color=
'#e3ded8')
ax.plot([x_O1,x_C1],[y_O1,y_C1],linewidth =9.0,
color='k')
ax.plot([x_O1,x_C1],[y_O1,y_C1],linewidth =6.0,
color='#e3ded8')
根據關鍵點O、O1的坐標,依次繪制鉸鏈O和鉸鏈O1,初時刻時繪制結果如圖1(b)所示。Python代碼如下:
ax.plot(x_O,y_O,markersize=12,c='k',marker='o')
ax.plot(x_O,y_O,markersize=8,c='w',marker='o')
ax.plot(x_O1,y_O1,markersize=12,c='k',marker='o')
ax.plot(x_O1,y_O1,markersize=8,c='w',marker='o')
根據關鍵點C、C1的坐標,繪制連桿CC1,初時刻時繪制結果如圖1(c)所示。Python代碼如下:
ax.plot([x_C,x_C1],[y_C,y_C1],linewidth =9.0,color='k')
ax.plot([x_C,x_C1],[y_C,y_C1],linewidth =6.0,
color='#e3ded8')
根據關鍵點C、C1的坐標,依次繪制鉸鏈C和鉸鏈C1。根據各關鍵點坐標,使用“text”函數在關鍵點旁標注對應字母,具體代碼不再贅述。初時刻時繪制結果如圖1(d)所示,動畫過程可關閉字母顯示。繪制鉸鏈C、C1的代碼如下:
ax.plot(x_C,y_C,markersize=12*0.5,c='k',marker='o')
ax.plot(x_C,y_C,markersize=8*0.5,c='w',marker='o')
ax.plot(x_C1,y_C1,markersize=12*0.5,c='k',marker
='o')
ax.plot(x_C1,y_C1,markersize=8*0.5,c='w',marker
='o')
(a)曲柄OC和曲柄O1C1
(b)鉸鏈O和鉸鏈O1
(c)連桿CC1
(d)平行四邊形機構
圖1? 平行四邊形機構繪制過程圖
3.3? 曲線平移可視化
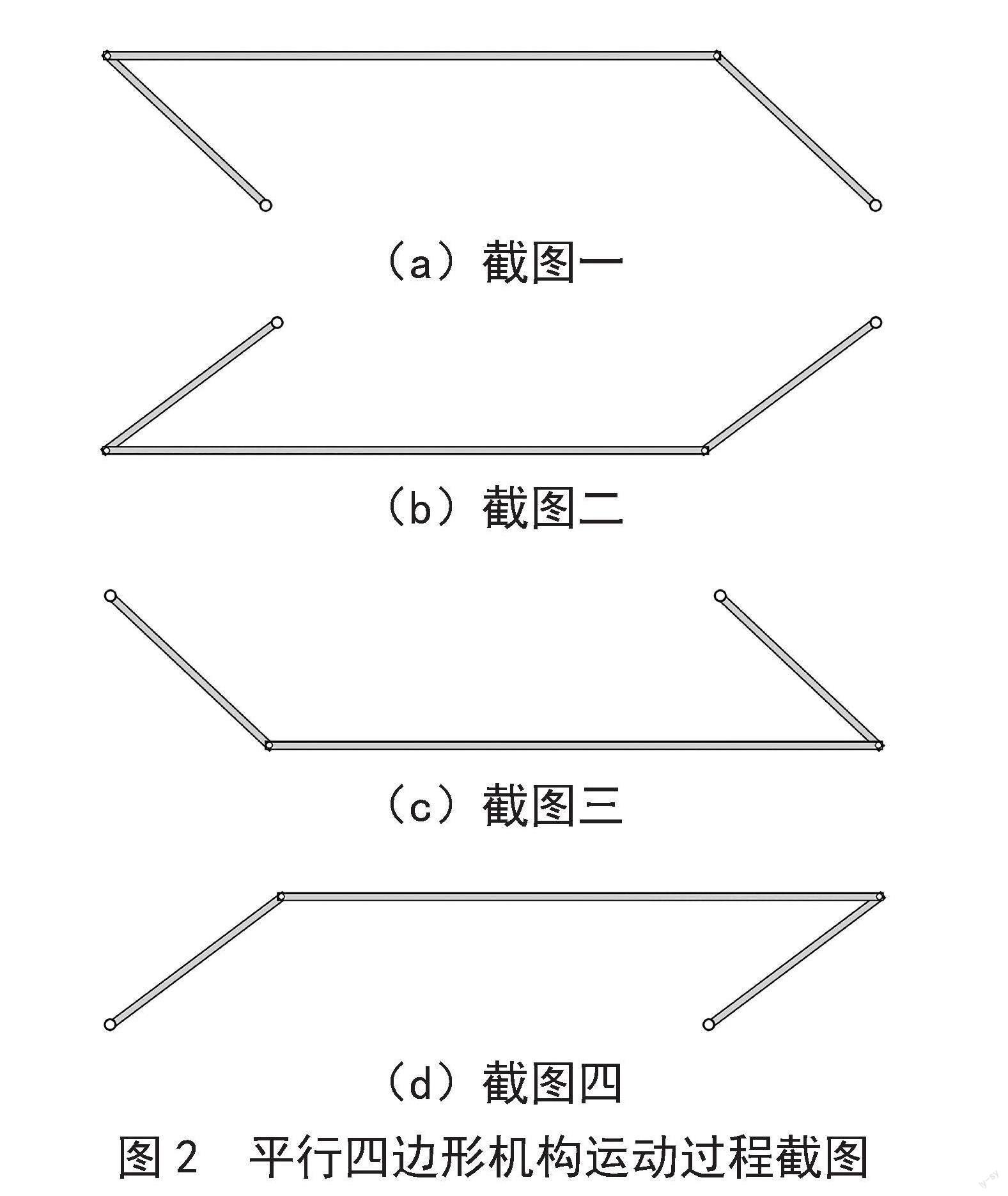
循環調用平行四邊形機構數據計算及繪制代碼,得到一系列動畫幀,最終可得到其運動動畫,也得到了做曲線平移的連桿的運動動畫。平行四邊形機構運動過程截圖如圖2所示(本文gif動畫已轉視頻上傳至B站https://space.bilibili.com/396001643)。Python代碼如下:
ani = animation.FuncAnimation(fig, update, range(310), init_func=init, interval=30)
ani.save('PY-donghua.gif', writer='imagemagick')
在平行四邊形機構運動過程中,連桿一直處于水平狀態,即其始終平行于初始位置,圖2展示了平移運動的此特點。
3.4? 曲線平移動點軌跡可視化
在連桿上任取兩動點M、N,坐標分別存儲在變量“x_M”“y_M”“x_N”“y_N”中,并存儲每一幀動點M、N和點C坐標于二維列表數組“xy_M_all”“xy_N_all”“xy_C_all”中,并在每一幀繪制所有歷史點,即得各點軌跡。曲線平移動點軌跡截圖如圖3所示,從左至右依次為點C、M、N的軌跡。Python代碼如下:
x_M=x_C+L/5*2
y_M=y_C
x_N=x_C+L/5*4
y_N=y_C
xy_C_all.append([x_C,y_C])
xy_M_all.append([x_M,y_M])
xy_N_all.append([x_N,y_N])
ax.plot(x_C,y_C,markersize=12*0.5,c='k',marker='o')
ax.plot(x_M,y_M,markersize=12*0.5,c='b',marker='o')
ax.plot(x_N,y_N,markersize=12*0.5,c='r',marker='o')
for ii in range(0,i,1*5):
ax.plot(xy_C_all[ii][0],xy_C_all[ii][1],markersize=12*0.5,c='k',marker='o')
ax.plot(xy_M_all[ii][0],xy_M_all[ii][1],markersize=12*0.5,c='b',marker='o')
ax.plot(xy_N_all[ii][0],xy_N_all[ii][1],markersize=12*0.5,c='r',marker='o')
從圖3可見,此做曲線平移的連桿上任意兩點的軌跡形狀相同,且為曲線(此例中為圓),且任一時刻,各動點都運動到軌跡的同一位置,從而說明平移運動的另一個特點——在每一瞬時,做平移運動的剛體上各點的速度相同,加速度也相同。
4? 結? 論
本研究將基于Python的可視化技術應用在曲線平移的教學中,使抽象的曲線平移知識具體化直觀化,降低了學習難度,從而提升了學習效果。詳細介紹了利用Python制作曲線平移動畫,既加深了學生對曲線平移的理解,也使學生初步掌握了繪制圖形及制作動畫等Python編程知識。將編程內容引入理論力學課程,使傳統理論課程與現代信息技術交叉融合,豐富了學生的信息技術知識,也進一步增強了學生對所學課程的興趣和信心。
參考文獻:
[1] 哈爾濱工業大學理論力學教研室.理論力學(Ⅰ):第8版 [M].北京:高等教育出版社,2016.
[2] 劉健智,程婷.GeoGebra軟件在物理可視化教學中的應用 [J].物理教師,2021,42(6):70-73.
[3] 陳林.基于GeoGebra的高中物理習題可視化教學研究 [D].蘇州:蘇州大學,2021.
[4] 許楊劍,阮洪勢,沈倩倩,等.材料力學教學中的編程實踐——應力狀態分析 [J].力學與實踐,2018,40(4):446-450.
[5] 李琳.平底頂桿凸輪機構的MATLAB動畫編程 [J].力學與實踐,2005(5):74-76.
[6] 闞文彬,李彤,葉純杰.MATLAB在運動學中的應用 [J].力學與實踐,2010,32(3):118-120.
[7] 田葉,高振海,宋海珍.Maple在剛體平面運動教學中的應用 [J].南陽師范學院學報,2011,10(9):88-90.
[8] 敖文剛,李勤,王歆.基于Matlab的理論力學計算機輔助教學 [J].力學與實踐,2013,35(1):83-86.
[9] 高云峰.Matlab求解理論力學問題系列(二) 典型機構的運動分析 [J].力學與實踐,2021,43(3):414-419.
[10] 郭子灃.理論力學動力學作業在線平臺的建立及其應用研究 [D].南昌:南昌大學,2020.
[11] 洪嘉振,劉鑄永,楊長俊.理論力學:第5版 [M].北京:高等教育出版社,2023.
[12] 孫桓,葛文杰.機械原理:第9版 [M].北京:高等教育出版社,2021.
作者簡介:張朋(1986—),男,漢族,河南南陽人,博士,講師,研究方向:計算力學。

