2023年全國(guó)乙卷圓錐曲線解法探討與推廣

賀鳳梅 李昌成

(1.鞏留縣高級(jí)中學(xué),新疆 伊犁 835400;2.烏魯木齊市第八中學(xué),新疆 烏魯木齊 830002)

直線與圓錐曲線的綜合題一直是高考命題的熱點(diǎn),也是學(xué)生學(xué)習(xí)的難點(diǎn),大部分學(xué)生對(duì)這部分知識(shí)的學(xué)習(xí)有畏懼心理.在學(xué)習(xí)過(guò)程中,他們僅停留在記憶相關(guān)概念、結(jié)論,或者模仿教材和教師的解題思路,并沒(méi)有真正理解概念、結(jié)論的意義,也沒(méi)有總結(jié)圓錐曲線中各種題型的內(nèi)在關(guān)聯(lián),或僅僅流于形式,因此考試時(shí)往往只能得一部分基礎(chǔ)分[1].據(jù)此,以此次高考試題中圓錐曲線的解答為契機(jī),談?wù)勛约旱目捶?以期拋磚引玉.

1 題目呈現(xiàn)

(1)求C的方程;

(2)過(guò)點(diǎn)(-2,3)的直線交C于P,Q兩點(diǎn),直線AP,AQ與y軸的交點(diǎn)分別為M,N,證明:線段MN的中點(diǎn)為定點(diǎn).

2 總體分析

此題是2023年全國(guó)乙卷的解答題第20題,屬于壓軸題.這道圓錐曲線題的第(1)問(wèn)實(shí)屬常規(guī)的送分題,而第(2)問(wèn)落腳點(diǎn)雖然是定點(diǎn)問(wèn)題,但與平時(shí)訓(xùn)練時(shí)見(jiàn)到的題的問(wèn)法還是有差異.考后筆者了解了一下,在考場(chǎng)上不少考生只是設(shè)出直線PQ方程的點(diǎn)斜式,與橢圓方程聯(lián)立,但由于計(jì)算復(fù)雜,沒(méi)有學(xué)會(huì)合理轉(zhuǎn)化,止步于此了.

其實(shí),直線與圓錐曲線的綜合問(wèn)題,主要是以位置關(guān)系為載體,所以根據(jù)題意設(shè)直線方程,與圓錐曲線進(jìn)行聯(lián)立,借助根與系數(shù)的關(guān)系進(jìn)行轉(zhuǎn)化求解;同時(shí)將問(wèn)題進(jìn)行分步拆解,需要設(shè)未知量時(shí)果斷設(shè)未知量以及必要的方程,最終設(shè)而不求,成功突破.筆者通過(guò)思考、解答與總結(jié),嘗試?yán)迩鍐?wèn)題的本質(zhì),現(xiàn)分享于此,以饗讀者.

3 試題解答

以下著重探討第(2)問(wèn).

視角1常規(guī)轉(zhuǎn)化.

解法1 (直線的斜截式方程聯(lián)合求解)

如圖1,易知直線PQ的斜率存在,設(shè)其方程為y=kx+m,過(guò)點(diǎn)(-2,3),所以m=2k+3.

①

圖1 解法1示意圖

設(shè)P(x1,y1),Q(x2,y2),

消y,整理得

(4k2+9)x2+8kmx+4m2-36=0,

△=64k2m2-4(4k2+9)(4m2-36)>0,

即m2<4k2+9.

由根與系數(shù)的關(guān)系,得

②

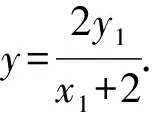
y1=kx1+m,y2=kx2+m.

③

聯(lián)合③整理,得

將②代入,繼續(xù)化簡(jiǎn)整理得

由①可得m-2k=3.

所以線段MN中點(diǎn)為定點(diǎn)(0,3)[2].

解法2 (直線的點(diǎn)斜式方程聯(lián)合求解)

設(shè)直線PQ方程為y-3=k(x+2),

即y=kx+(2k+3).

(4k2+9)x2+8k(2k+3)x+4(2k+3)2-36=0.

④

不妨設(shè)直線AM為y=k1(x+2),令x=0,則y=2k1,所以點(diǎn)M(0,2k1).

同理N(0,2k2).

故線段中點(diǎn)坐標(biāo)為N(0,k1+k2).

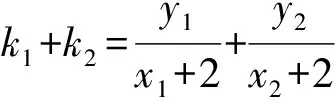
將④代入整理,得

所以線段MN中點(diǎn)為定點(diǎn)(0,3).

評(píng)注以上兩種解法大同小異,解法1設(shè)直線PQ的斜截式方程,將點(diǎn)(-2,3)代入,明確數(shù)量關(guān)系m=2k+3;同時(shí)與橢圓方程進(jìn)行聯(lián)立,設(shè)點(diǎn)的坐標(biāo),根據(jù)韋達(dá)定理得出兩根之和與兩根之積待用.接著進(jìn)行下一步轉(zhuǎn)化,結(jié)合條件設(shè)法將點(diǎn)M的坐標(biāo)表示出來(lái),再利用同一法表示點(diǎn)N的坐標(biāo),進(jìn)而表示出MN中點(diǎn)的坐標(biāo).此時(shí),隨著問(wèn)題的分步求解,發(fā)現(xiàn)本質(zhì)上就是求兩直線AP與AQ的斜率之和為定值.分式進(jìn)行通分,非對(duì)稱性轉(zhuǎn)化為對(duì)稱性,代入韋達(dá)定理的式子化簡(jiǎn)等都屬于常規(guī)操作.因此,解決問(wèn)題的關(guān)鍵還是在于我們拿到試題后進(jìn)行思考、分析、整合,將未知轉(zhuǎn)化為已知,將陌生轉(zhuǎn)化為熟悉,這也是當(dāng)前新課改后國(guó)家選拔人才的要求.解法2只是設(shè)直線方程不同,求解路徑稍有不同,進(jìn)行部分分離變量后,式子更簡(jiǎn)單明了,這也需要通過(guò)一定的訓(xùn)練才能達(dá)到熟能生巧,靈活變通,不再贅述.

視角2齊次化轉(zhuǎn)化.

解法3(平移齊次化求解)

將圖象整體向右平移兩個(gè)單位,則點(diǎn)(-2,3)平移至(0,3),點(diǎn)A(-2,0)平移至(0,0).

相應(yīng)直線PQ的方程可設(shè)為

y=kx+3,

將平移后的橢圓化簡(jiǎn)整理,得

4y2+9x2-36x=0.

齊次化,得

進(jìn)一步整理得

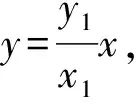
從而平移后線段MN中點(diǎn)坐標(biāo)為(2,3).

故線段MN中點(diǎn)為定點(diǎn)(0,3),得證[3].

解法4(配湊齊次化求解)

將4y2+9x2-36=0進(jìn)行配湊得

4y2+9(x+2)2-36(x+2)=0.

與直線y=k(x+2)+3聯(lián)立并整理,得

4y2+(9k+12)(x+2)2-12y(x+2)=0.

故線段MN中點(diǎn)為定點(diǎn)(0,3),得證.

評(píng)注解法3是將點(diǎn)A平移至坐標(biāo)原點(diǎn),其余點(diǎn)與直線、橢圓均移至相應(yīng)的位置,通過(guò)齊次化轉(zhuǎn)化,大大減少了運(yùn)算量.不過(guò)此法建議給學(xué)習(xí)程度好、學(xué)有余力的同學(xué)嘗試,一定要講清原理,平移前與平移后的關(guān)系,再輔以適當(dāng)?shù)木毩?xí)加以鞏固,這樣才能收到成效.解法4則是通過(guò)構(gòu)造法整體處理,同樣需要老師給學(xué)生講清原理,感興趣的同仁不妨一試!

視角3 向量法.

解法5(設(shè)線求點(diǎn)及向量共線求解)

設(shè)直線AM:y=m(x+2),AN:y=n(x+2),則M(0,2m),N(0,2n),線段MN中點(diǎn)坐標(biāo)為(0,m+n),即證m+n為定值.

設(shè)P(x1,y1),Q(x2,y2),

(4m2+9)x2+16m2x+16m2-36=0.

易得12m-4m2-9=12n-4n2-9.

又m≠n,所以m+n=3.

故線段MN中點(diǎn)為定點(diǎn)(0,3),得證.

視角4曲線系.

解法6 (借助曲線系巧妙消元代點(diǎn)求解)

結(jié)合解法5,經(jīng)過(guò)三點(diǎn)的二次曲線為

[y-m(x+2)][y-n(x+2)]=0.

即y2-(m+n)(x+2)y+mn(x+2)2=0.

消去y2,得

顯然x≠-2,所以

即PQ的直線方程過(guò)點(diǎn)(-2,3),

代入整理并求解得m+n=3.

故線段MN中點(diǎn)為定點(diǎn)(0,3),得證.

評(píng)注曲線系在課本上有涉及,只是平時(shí)使用較少,所以大家并不熟悉,從以上解答來(lái)看,若能理解、掌握并應(yīng)用到解題中去,確實(shí)有不一樣的效果,大家可以根據(jù)需要選擇!

4 嘗試推廣

此題的出題背景本質(zhì)上就是極點(diǎn)極線,可以推廣得到以下兩個(gè)結(jié)論.

以上是焦點(diǎn)在y軸上的橢圓的一般結(jié)論,對(duì)于焦點(diǎn)在x軸上的橢圓的一般結(jié)論,大家可以參照得出,不再贅述.

5 試題鏈接

(1)求E的方程;

簡(jiǎn)析該題中的同一法求解是本次真題中所用到的方法,包括直線過(guò)定點(diǎn)問(wèn)題.只是設(shè)置的問(wèn)題情境不盡相同.因此,在平時(shí)的學(xué)習(xí)及高考復(fù)習(xí)備考中,我們一定要關(guān)注和積累一些通性通法,所謂萬(wàn)變不離其宗,很多試題均可以追本溯源,不管在知識(shí)上還是方法上,都有異曲同工之妙!

簡(jiǎn)析該題是比較典型的已知斜率之和為定值,證明直線過(guò)定點(diǎn)問(wèn)題,可以利用文中的常規(guī)方法求解,也可以利用平移齊次化或構(gòu)造齊次化求解.相信大家只要學(xué)會(huì)整合與反思,一定能有收獲!

6 結(jié)束語(yǔ)

高中圓錐曲線的試題對(duì)學(xué)生思維能力及計(jì)算能力的要求都很高,教師在教學(xué)時(shí)要把握好重、難點(diǎn),循序漸進(jìn),保證學(xué)生在夯實(shí)基礎(chǔ)的前提下,逐步提高難度.教學(xué)過(guò)程中,建議結(jié)合學(xué)生的學(xué)情來(lái)規(guī)劃教學(xué)的進(jìn)度和難易程度,耐心細(xì)致地解答學(xué)生提出的問(wèn)題及計(jì)算中的盲點(diǎn)及卡點(diǎn).同時(shí)還需要有意識(shí)地培養(yǎng)學(xué)生的數(shù)形結(jié)合的能力,從而穩(wěn)步提高圓錐曲線的教學(xué)效率.

命題專家指出,根據(jù)《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017年版)》的要求,今年高考數(shù)學(xué)全國(guó)卷全面考查考生的數(shù)學(xué)核心素養(yǎng),充分體現(xiàn)基礎(chǔ)性、應(yīng)用性以及創(chuàng)新性的考查要求,突出理性思維,發(fā)揮數(shù)學(xué)學(xué)科在人才選拔中的重要作用.在全面推行素質(zhì)教育的今天,新一輪國(guó)家教育課程改革之際,對(duì)新教材、學(xué)生新的學(xué)習(xí)方式的研究與探討顯得尤為重要.只有充分發(fā)揮青年一代的數(shù)學(xué)素養(yǎng),才能提高全民素質(zhì),造就新一代的高質(zhì)量新型人才!