以“問題提出”促進(jìn)小學(xué)數(shù)學(xué)課堂“教、學(xué)、評”一致性

李林

在小學(xué)數(shù)學(xué)教育中，“教、學(xué)、評”一致性一直是教師和學(xué)生關(guān)注的重點。然而，傳統(tǒng)的教學(xué)方式往往以知識的傳授為主，缺乏對學(xué)生思維能力和問題解決能力的培養(yǎng)。在“教”的階段利用“問題提出”可以為學(xué)生做指引；在“學(xué)”的階段利用“問題提出”可以作為學(xué)生學(xué)習(xí)的目標(biāo)；在“評”的階段利用“問題提出”可以檢測學(xué)生的學(xué)習(xí)水平。因此，教師研究“問題提出”在小學(xué)數(shù)學(xué)“教、學(xué)、評”一致性方面具有重要的意義，能夠?qū)崿F(xiàn)學(xué)生數(shù)學(xué)學(xué)習(xí)的良性循環(huán)。

一、“問題提出”促進(jìn)“教、學(xué)、評”一致性的理論基礎(chǔ)

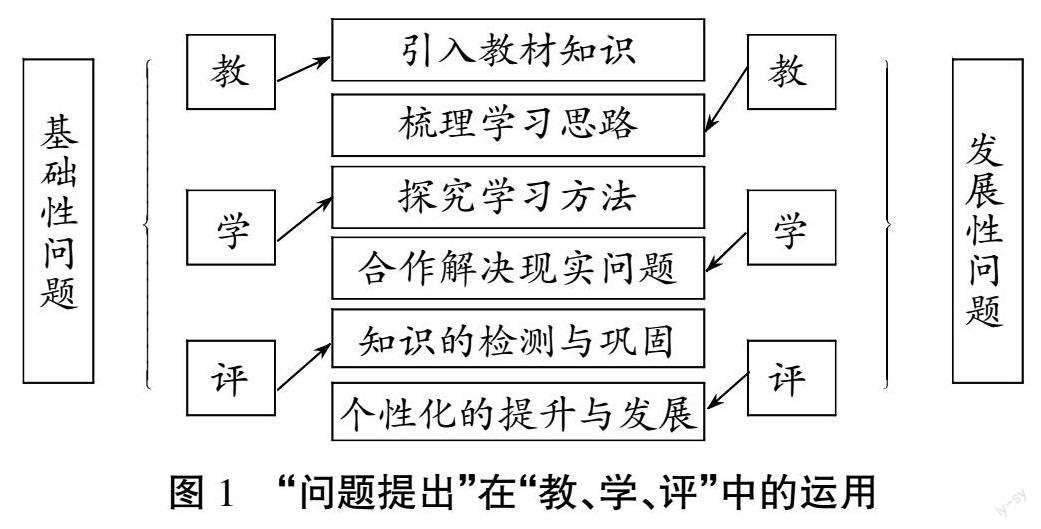
“教、學(xué)、評”三個環(huán)節(jié)相互依存，相互補充。“教”的環(huán)節(jié)主要目的為引入教材知識，讓學(xué)生在學(xué)習(xí)教材知識時具備正確的思維和思路；“學(xué)”的環(huán)節(jié)則是學(xué)生對學(xué)習(xí)方法的拓展，在解決問題時能夠觸類旁通、舉一反三；“評”的環(huán)節(jié)則是對學(xué)生知識掌握程度的一種檢測或者對已掌握的知識的一種鞏固。為了使“教、學(xué)、評”三個階段更加完善和豐富，教師在利用“問題提出”時需設(shè)計基礎(chǔ)性問題和發(fā)展性問題。基礎(chǔ)性問題和發(fā)展性問題在“問題提出”中的體現(xiàn)如圖1所示。

所謂基礎(chǔ)性問題，就是以理解并掌握知識和技能為根本目的，指導(dǎo)學(xué)生在問題情境的基礎(chǔ)上聯(lián)系已有知識經(jīng)驗所提出的有關(guān)教學(xué)內(nèi)容的問題，目標(biāo)較為單一，指向亦較清晰，不同學(xué)生均能提出與自己水平相符的問題并共同建構(gòu)有效問題序列，以此作為學(xué)習(xí)素材來指明探究方向和推動學(xué)生全員參與；發(fā)展性問題指以思維和能力培養(yǎng)為高層次目標(biāo)，以開放性問題為主，訓(xùn)練學(xué)生的發(fā)散性思維，為學(xué)習(xí)提供更多資源。發(fā)展性問題目標(biāo)呈現(xiàn)多元性，學(xué)生所提問題有多種可能性，需綜合應(yīng)用多種知識和技能。發(fā)展性問題也可成為學(xué)生學(xué)習(xí)水平和思維的一種體現(xiàn)。“問題提出”作為一種教學(xué)手段、學(xué)習(xí)目標(biāo)及評價工具，它與教學(xué)、學(xué)習(xí)、評價等活動息息相關(guān)。精心設(shè)計、有效實施和正確把握提問的教學(xué)活動能夠在教學(xué)中尋找“教、學(xué)、評”之間的融通點，并推動教學(xué)一體化和螺旋式地向上發(fā)展。

二、“問題提出”在“教、學(xué)、評”一致性教學(xué)中的實踐

（一）“問題提出”在“教”環(huán)節(jié)中的應(yīng)用

1.基礎(chǔ)性問題引入教材知識

在探究“雞兔同籠”問題之前，教師需要為學(xué)生創(chuàng)建學(xué)習(xí)“雞兔同籠”的環(huán)境，引入“雞兔同籠”的知識。

師：大家知道1只雞2條腿，1只兔子4條腿，如果將2只雞和3只兔子放進(jìn)一個籠子里面，那么總共有多少條腿呢？

生：2只雞總共有2×2=4條腿，3只兔子總共有3×4=12條腿，因此總共有16條腿。

師：很好，反過來說，已知總共有16條腿，5個頭，可知雞有2只，兔子有3只。那么如果說有28條腿，8個頭，雞兔各有多少呢？

生：28條腿比16條腿多了28-16=12條腿，并且8-5=3個頭，恰好一只兔子四條腿，因此多了3只兔子，即兔子6只，雞2只。

師：很好！如果是35個頭和94條腿呢？今天我們要講解一個非常有趣的問題！相傳在一個神秘的農(nóng)場，農(nóng)場主人出門時發(fā)現(xiàn)了一只大籠子，里面有很多只雞和兔子。他好奇地數(shù)了一下，總共有35個頭和94只腿。農(nóng)場主想知道這個籠子里究竟有多少只雞和兔子，但雞和兔子混在一起，根本無法數(shù)清。同學(xué)們，你們知道籠子里面分別有多少只雞和多少只兔子嗎？

生：……

師：我們可以假設(shè)一下，如果有35只兔子會有多少條腿？

生：如果是35只兔子，那么1只兔子4條腿，35×4=140，而總共只有94條腿，說明是不對的。

師：如果35只雞呢？

生：如果35只雞，那么1只雞2條腿，35×2=70，與94條腿不符，也是不對的。

師：嗯，很好。大家知道嗎？在我國古代數(shù)學(xué)著作《孫子算經(jīng)》中也記錄了這一問題，那么古人是怎么解決這一問題的呢？

這樣引入案例，既能激發(fā)學(xué)生的學(xué)習(xí)興趣，又能鍛煉學(xué)生的思維能力。在引入之后，教師可以繼續(xù)展開課堂教學(xué)，進(jìn)一步引導(dǎo)學(xué)生學(xué)習(xí)相關(guān)的數(shù)學(xué)知識。

2.發(fā)展性問題梳理學(xué)習(xí)思路

在學(xué)生了解“雞兔同籠”這一問題的概念之后，教師可以繼續(xù)提出發(fā)展性問題，向?qū)W生講解“雞兔同籠”問題的解決策略。

師：通過上述計算可以發(fā)現(xiàn)，雞和兔的數(shù)量都不是35只，那么我們可以思考一下，假設(shè)兔子是34只，雞是1只，總共有多少條腿？

生：34×4+1×2=138，仍然不是94條腿。

師：那么如果兔子是33只，雞是2只呢？

生：33×4+2×2=136，也是不正確的。

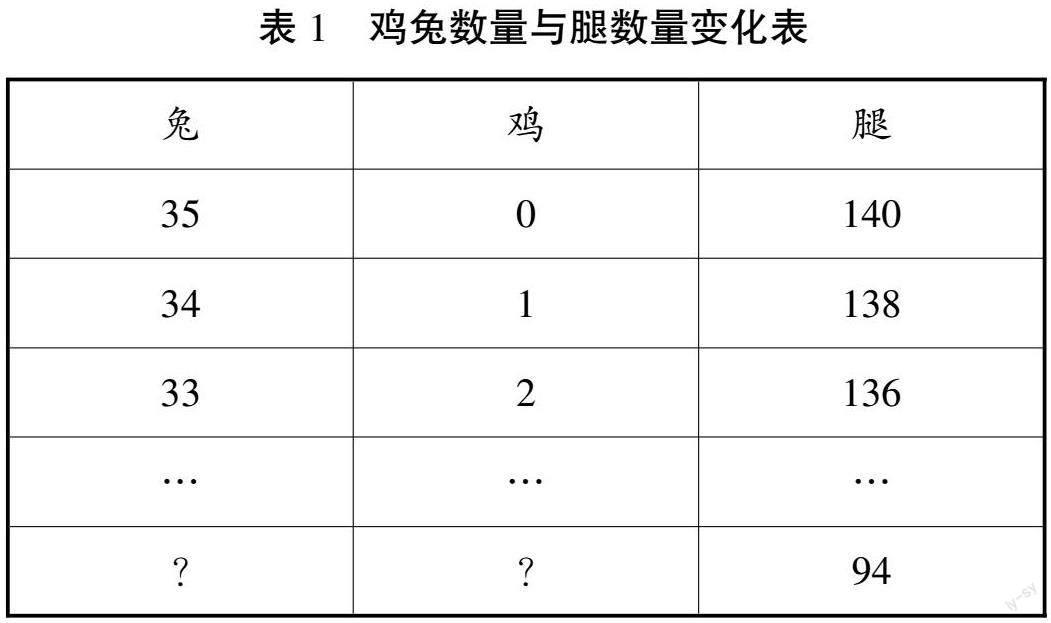
師：同學(xué)們，通過上述數(shù)據(jù)你有沒有發(fā)現(xiàn)規(guī)律呢？當(dāng)兔子是35只，雞0只的時候，腿是140條；當(dāng)兔子是34只，雞1只的時候腿是138條；當(dāng)兔子33只，雞2只的時候，腿136。如下表1所示。

生：通過上表我發(fā)現(xiàn)，當(dāng)兔子數(shù)量減少1只的時候，腿的總條數(shù)就會減少2條。因此，當(dāng)腿的總條數(shù)為94時，腿的總條數(shù)減少了140-94=46，兔子的數(shù)量減少了46÷2=23，兔子的總數(shù)為35-23=12只。因此，當(dāng)兔子數(shù)量為12只，雞的數(shù)量為23只時，符合題目要求。

通過上述發(fā)展性問題的引導(dǎo)，學(xué)生逐漸掌握了解決“雞兔同籠”問題的方法。通過這樣的思考過程，教師引導(dǎo)學(xué)生通過觀察、推理和簡單的數(shù)學(xué)運算來解決“雞兔同籠”問題。這樣的方法注重培養(yǎng)小學(xué)生的觀察力、邏輯思維和問題解決能力，符合小學(xué)生的認(rèn)知水平。

（二）“問題提出”在“學(xué)”這一環(huán)節(jié)中的應(yīng)用

如果說“教”的環(huán)節(jié)注重對學(xué)生的課堂引入和學(xué)習(xí)方法的引導(dǎo)，那么“學(xué)”的環(huán)節(jié)則是學(xué)生深刻掌握這一學(xué)習(xí)方法的關(guān)鍵。在“教”的環(huán)節(jié)中學(xué)生基本掌握了“雞兔同籠”問題的解決思路，可以通過列表格的方式來計算雞和兔的數(shù)量，但需要在“學(xué)”的環(huán)節(jié)進(jìn)行拓展。另外，現(xiàn)實中的問題往往是復(fù)雜多變的，因此，學(xué)生需要從基礎(chǔ)性問題中認(rèn)識到問題的本質(zhì)。

在學(xué)生掌握“雞兔同籠”這一問題的解決方法之后，教師可以引導(dǎo)學(xué)生進(jìn)一步思考：有沒有更加快捷的解決方法？

師：在上面我們用列表格的方式解決了“雞兔同籠”的問題，大家認(rèn)真觀察一下上述表格，思考一下有沒有解決問題的捷徑。

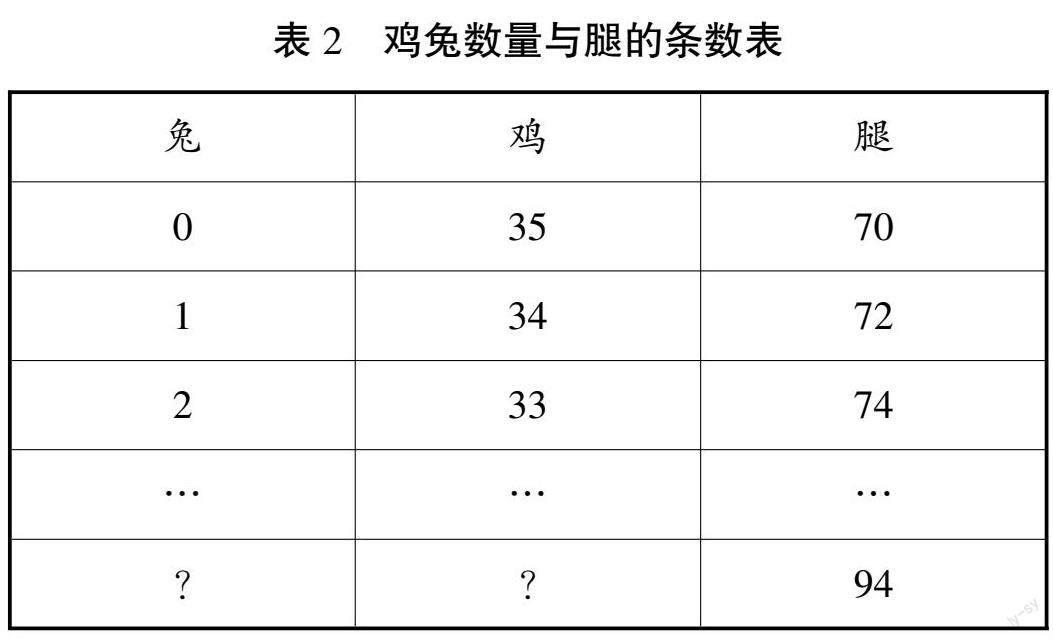
生：上述表格是由兔子的數(shù)量開始計算的，我們還可以從雞的數(shù)量進(jìn)行推理，也可以得到最終數(shù)量。（見表2）根據(jù)表2可以發(fā)現(xiàn)，雞的數(shù)量每減少1只，腿的條數(shù)就增加2條，我們可以通過這一規(guī)律來計算雞的數(shù)量，進(jìn)而計算兔的數(shù)量。

師：嗯，很好。這兩種方法較為相似，但是70到94的距離，相較于140到94距離更近，如果通過列表的方式進(jìn)行計算就會更快得出答案。那么問題來了，我們?nèi)绾卧趦H知道雞兔總數(shù)和腿的條數(shù)的情況下，判斷哪一種方式更快呢？

生：先假設(shè)籠子里面只有一種動物，雞或兔，然后算出只有一種動物時腿的條數(shù)，然后對比哪一個數(shù)字距離已知腿的數(shù)量最近，從而判斷哪一種方式更加便捷。

師：如果不用列表的方式，還有其他方法計算雞和兔的數(shù)量嗎？

生：老師，因為雞有2條腿，兔子有4條腿，兔子腿的數(shù)量為雞的2倍，根據(jù)已知的條件，即2雞+4兔=94；雞+兔=35，也可以計算出雞和兔的數(shù)量。

通過問題引導(dǎo)可以激發(fā)學(xué)生的敏銳觀察力，學(xué)生可以由表1推導(dǎo)出表2，從而得出解決問題更快的方法。另外，教師通過問題的指引，可以讓學(xué)生跳出列表格的方法，將雞和兔虛擬為未知數(shù)，從而通過列式子的方式解決問題。

（三）“問題提出”在“評”環(huán)節(jié)的運用

1.利用問題對學(xué)生的知識進(jìn)行檢測和鞏固

教師通過簡單的口頭提問，讓學(xué)生計算雞和兔子的總數(shù)或腿的總數(shù)，從而鍛煉學(xué)生的口算能力和思維能力。

師：如果有36只雞和兔子在一個籠子里，它們的總腿數(shù)是100條，請問雞和兔子各有多少只？

通過這樣的問題，教師可以評估學(xué)生能否正確應(yīng)用加法、乘法等來解決問題。教師還可以進(jìn)一步對“雞兔同籠”問題進(jìn)行演變，增加難度，檢驗學(xué)生的應(yīng)變能力。

師：假設(shè)大輪胎為15 kg，小輪胎為5 kg，總重量為225 kg，如何計算大小輪胎的個數(shù)？

通過以上的問題提問方式，教師不僅能夠檢測學(xué)生對“雞兔同籠”問題的理解和運用能力，還可以鞏固學(xué)生對算術(shù)運算的掌握程度。同時，這樣的問題能促進(jìn)學(xué)生的邏輯思考和問題解決能力的提升。

2.個性化的提升與發(fā)展

根據(jù)學(xué)生性格、興趣等因素，創(chuàng)設(shè)多樣化的問題情境，設(shè)計不同情境的“雞兔同籠”問題，如農(nóng)場、動物園、寵物店等，以激發(fā)學(xué)生的興趣和好奇心。教師創(chuàng)設(shè)多樣化的問題情境，激發(fā)學(xué)生的學(xué)習(xí)興趣，并提高學(xué)生在不同情境下的思考和解決問題能力，鼓勵學(xué)生尋求多種解題方法，如圖形推理、邏輯推理、模式識別等。

師：你能用圖形或圖表表示雞和兔子的數(shù)量嗎？

師：你能發(fā)現(xiàn)不同雞和兔子數(shù)量之間的規(guī)律嗎？

師：你能想到其他類似的數(shù)學(xué)問題嗎？如果除了雞和兔子，還有其他動物，問題會發(fā)生什么變化？

除了基本的“雞兔同籠”問題，教師還可以提供一些更具挑戰(zhàn)性的拓展問題，如增加動物數(shù)量、腿的類型變化等。這樣的問題可以給予學(xué)有余力的學(xué)生更大的學(xué)習(xí)空間，促進(jìn)他們深入思考，提升其拓展運用知識的能力。通過以上的個性化問題評價方式，教師能夠針對學(xué)生的興趣和能力差異，激發(fā)學(xué)生的學(xué)習(xí)動力，提高其學(xué)習(xí)效果。

三、結(jié)論

通過對小學(xué)數(shù)學(xué)課堂中“問題提出”的研究和實踐，發(fā)現(xiàn)“問題提出”能夠有效促進(jìn)小學(xué)數(shù)學(xué)“教、學(xué)、評”的一致性。“問題提出”可以激發(fā)學(xué)生的思維能力，培養(yǎng)學(xué)生解決問題的能力，提高學(xué)生的學(xué)習(xí)興趣和學(xué)習(xí)動力。同時，“問題提出”也使教師更加注重對學(xué)生理解和應(yīng)用能力的培養(yǎng)，從而提高教學(xué)效果。在具體的課堂教學(xué)中，教師還應(yīng)該結(jié)合信息技術(shù)為學(xué)生呈現(xiàn)豐富的視聽效果，以提升學(xué)生的課堂專注力。

（作者單位：迭部縣多兒鄉(xiāng)中心小學(xué)）

編輯：陳鮮艷