高中數(shù)學(xué)自制教具的創(chuàng)新實(shí)踐及策略分析

孫家和 朱金鳳

摘? 要：以人教A版《普通高中教科書·數(shù)學(xué)》的教學(xué)實(shí)踐為基礎(chǔ)，類比圓規(guī)和圓第二規(guī)教具的發(fā)明過程，從圓錐曲線軌跡的實(shí)驗(yàn)原理抽象出數(shù)學(xué)模型，啟發(fā)學(xué)生制作拋物線規(guī)、圓錐曲線規(guī). 總結(jié)自制教具的原理和一般方法，為學(xué)生設(shè)計(jì)其他數(shù)學(xué)教具提供參考，從而培養(yǎng)學(xué)生的創(chuàng)新意識(shí)和實(shí)踐能力，發(fā)展學(xué)生的數(shù)學(xué)抽象和數(shù)學(xué)建模等素養(yǎng).

關(guān)鍵詞：教具；圓規(guī)；拋物線規(guī)；圓錐曲線規(guī)

中圖分類號(hào)：G633.65???? 文獻(xiàn)標(biāo)識(shí)碼：A???? 文章編號(hào)：1673-8284（2024）01-0023-04

引用格式：孫家和，朱金鳳. 高中數(shù)學(xué)自制教具的創(chuàng)新實(shí)踐及策略分析［J］. 中國數(shù)學(xué)教育（高中版），

2024（1）：23-26.

基金項(xiàng)目：2022年度安徽省社會(huì)科學(xué)創(chuàng)新發(fā)展研究課題——中華優(yōu)秀傳統(tǒng)文化融入高中數(shù)學(xué)教學(xué)的實(shí)踐研究（2022CX191）；

安徽省教育科學(xué)研究項(xiàng)目——基于新課標(biāo)的數(shù)學(xué)建模能力評(píng)價(jià)的實(shí)踐研究（JK18008）.

作者簡介：孫家和（1978— ），男，高級(jí)教師，主要從事中學(xué)數(shù)學(xué)教育教學(xué)研究；

朱金鳳（1991— ），女，一級(jí)教師，主要從事高中數(shù)學(xué)教育教學(xué)研究.

圓規(guī)是一種數(shù)學(xué)作圖工具，最早出現(xiàn)在我國的夏朝，《史記·夏本紀(jì)》中就記載了大禹治水“左準(zhǔn)繩，右規(guī)矩”. 在公元前15世紀(jì)的甲骨文中，已有“矩”“規(guī)”二字，當(dāng)時(shí)稱為“規(guī)”，即圓規(guī). 人類借助圓的定義發(fā)明了圓規(guī). 圓錐曲線還包括橢圓、拋物線和雙曲線，有圓規(guī)，能否有拋物線規(guī)、橢圓規(guī)、雙曲線規(guī)，甚至是統(tǒng)一的圓錐曲線規(guī)呢？

一、追根溯源——圓第二規(guī)

圓的定義有很多種，其中最常見的是“平面內(nèi)到定點(diǎn)的距離等于定長的點(diǎn)的軌跡”，不妨稱為“第一定義”.“第一定義”可以理解為模型“平面內(nèi)，一條線段繞著它的一個(gè)端點(diǎn)旋轉(zhuǎn)一周，它的另一個(gè)端點(diǎn)所形成的軌跡叫做圓”. 由圓的定義建立模型，發(fā)明了圓規(guī)，使用圓規(guī)時(shí)可以先確定圓規(guī)針尖的位置，即先確定圓心，再調(diào)節(jié)圓規(guī)兩腳之間的距離，即確定半徑，另一只腳繞著針尖旋轉(zhuǎn)一周，即可作出圓. 可以看出，圓規(guī)作圖的原理中有兩個(gè)核心要素，即圓心與半徑.

根據(jù)對圓的性質(zhì)的探究，給出了圓的一種衍生定義——“平面內(nèi)到兩定點(diǎn)張角為90°的點(diǎn)的軌跡叫做圓”. 類比圓規(guī)的發(fā)明過程，是否可以根據(jù)圓的衍生定義建立模型，發(fā)明其他畫圓的教具呢？

通過分析，建立如圖1所示的模型. 圓的衍生定義中的兩個(gè)定點(diǎn)可以看作圖1中的圓的直徑的端點(diǎn)A和端點(diǎn)B，當(dāng)點(diǎn)C與點(diǎn)A，B不重合時(shí)，只要保證∠ACB的大小始終為直角，點(diǎn)C所形成的軌跡即為圓. 要將此模型轉(zhuǎn)化為實(shí)物，選定兩個(gè)定點(diǎn)并不難實(shí)現(xiàn)，需要重點(diǎn)解決的問題是始終保證∠ACB為直角. 如圖2，筆者查閱文獻(xiàn)，結(jié)合生活經(jīng)驗(yàn)，在直桿AD與BE之間固定直角架C，直角架C可以保證在滑動(dòng)直桿AD與BE時(shí)，∠ACB始終為直角，且直角架C上安裝有畫筆，可以實(shí)現(xiàn)畫圓功能. 因此，可以借助圓的衍生定義建立模型設(shè)計(jì)畫圓裝置，筆者將其稱為圓第二規(guī).

圓的第一定義來源于人們對生活模型的歸納總結(jié)，即數(shù)學(xué)來源于生活. 人們又以圓的第一定義原理為模型，創(chuàng)造發(fā)明了圓規(guī)教具，即數(shù)學(xué)是對現(xiàn)實(shí)生活的抽象. 進(jìn)一步對圓的性質(zhì)進(jìn)行研究，衍生出圓的其他定義，再借助圓的衍生定義建立模型，設(shè)計(jì)圓第二規(guī)，實(shí)現(xiàn)再發(fā)明、再創(chuàng)造，提高了學(xué)生發(fā)現(xiàn)問題、提出問題、分析問題和解決問題的能力，培養(yǎng)了數(shù)學(xué)建模和數(shù)學(xué)抽象素養(yǎng). 具體探究過程如圖3所示.

二、類比創(chuàng)造——拋物線規(guī)

圓是圓錐曲線中比較簡單的一類曲線，類比圓規(guī)與圓第二規(guī)教具的建模與創(chuàng)造過程，是否可以嘗試引導(dǎo)學(xué)生研究其他曲線規(guī)呢？

如圖4，人教A版《普通高中教科書·數(shù)學(xué)》選擇性必修第一冊（以下統(tǒng)稱“教材”）中利用信息技術(shù)探究拋物線的軌跡，得到拋物線的定義是：平面內(nèi)與一定點(diǎn)和一定直線（定直線不經(jīng)過定點(diǎn)）的距離相等的點(diǎn)的軌跡. 教師借助GeoGebra軟件進(jìn)行動(dòng)畫演示（如圖5），讓學(xué)生直觀感悟軌跡的生成過程. 同樣可以發(fā)現(xiàn)，拋物線軌跡的生成離不開兩個(gè)非常重要的因素：一個(gè)定點(diǎn)與一條定直線. 類比畫圓，引導(dǎo)學(xué)生根據(jù)拋物線的定義設(shè)計(jì)一個(gè)可以畫拋物線的作圖裝置. 裝置設(shè)計(jì)的關(guān)鍵是確定一個(gè)定點(diǎn)與一條定直線，技術(shù)難點(diǎn)是在點(diǎn)M的運(yùn)動(dòng)過程中，始終保證[MF=MH]（如圖4）.

師生共同討論后，給出兩種設(shè)計(jì)方案，如圖6和圖7所示. 兩種方案的原理相同，區(qū)別是使用的材料不同. 設(shè)計(jì)的方案是否具有可行性呢？通過CAD軟件優(yōu)化得到最終平面設(shè)計(jì)圖方案，如圖8（a）所示；再通過機(jī)械軟件SolidWorks2012進(jìn)行實(shí)驗(yàn)?zāi)M，如圖8（b）所示. 發(fā)現(xiàn)該裝置可行性較高，操作性較好. 這是一種多功能拋物線作圖裝置，筆者將其稱為“拋物線規(guī)”.

對于圖7，畫橢圓的流程是：把②從①拆下；在繪圖線上繪制平面直角坐標(biāo)系；調(diào)整③中木條的長度；將②⑤固定在橢圓焦點(diǎn)的位置；將筆插入④中，開始繪圖. 對于圖8，通過按鈕10和按鈕11調(diào)節(jié)小型電動(dòng)伸縮桿7和電動(dòng)伸縮桿8的長度，確定其長度，然后將筆放入空心鉸接鏈9，畫出相應(yīng)的曲線.

上述教具的開發(fā)，先從軌跡生成的原理出發(fā)建立模型，確定教具結(jié)構(gòu)方案，根據(jù)結(jié)構(gòu)特征選定材料，再借助機(jī)械軟件SolidWorks2012進(jìn)行信息技術(shù)實(shí)驗(yàn)?zāi)M，最后完成教具的設(shè)計(jì)與發(fā)明，具體探究過程如圖9所示.

三、歸納拓展——圓錐曲線規(guī)

借助一個(gè)定點(diǎn)與一條定線段或定直線可以畫圓和拋物線，能否作出其他圓錐曲線呢？與拋物線的定義類似，教材中也呈現(xiàn)了橢圓和雙曲線的其他定義.

教材第113頁例6：動(dòng)點(diǎn)[Mx，y]與定點(diǎn)[F4，0]的距離和M到定直線[l：x=254]的距離的比是常數(shù)[45]，求動(dòng)點(diǎn)M的軌跡.

如圖10，易求得動(dòng)點(diǎn)M的軌跡是橢圓[x225+y29=1].

教材第125頁例5：動(dòng)點(diǎn)[Mx，y]與定點(diǎn)[F4，0]的距離和它到定直線[l：x=94]的距離的比是常數(shù)[43]，求動(dòng)點(diǎn)M的軌跡.

如圖11，易求得動(dòng)點(diǎn)M的軌跡是雙曲線[x29-y27=1].

以上兩道例題，題干中均出現(xiàn)關(guān)鍵元素定點(diǎn)和定直線，本質(zhì)上給出了橢圓與雙曲線的另外一種定義，不妨稱為“第二定義”. 利用GeoGebra軟件從形的角度進(jìn)行直觀操作（如圖12和圖13），可以驗(yàn)證利用一個(gè)定點(diǎn)和一條定直線確實(shí)可以作出橢圓和雙曲線的圖象.

同樣是借助一個(gè)定點(diǎn)和一條定直線，為何作出的曲線有的是拋物線，有的是橢圓，有的是雙曲線呢？再將三個(gè)實(shí)驗(yàn)進(jìn)行深入的對比分析.

通過GeoGebra軟件動(dòng)畫演示與觀察，不難發(fā)現(xiàn)圖中[MF]和[MH]比值存在差異，借助GeoGebra軟件度量技術(shù)，驗(yàn)證和總結(jié)出如下規(guī)律：當(dāng)[MFMH=1]時(shí)，點(diǎn)M形成的軌跡是拋物線；當(dāng)[01]時(shí)，點(diǎn)M形成的軌跡是雙曲線.

在上述實(shí)驗(yàn)結(jié)果的基礎(chǔ)上進(jìn)一步思考：類比拋物線和圓的作圖工具，能否發(fā)明一種可以畫橢圓和雙曲線的作圖工具呢？不難想到，可以利用[MFMH]的比值來控制，發(fā)明一種集拋物線、橢圓、雙曲線功能于一體的作圖教具.

借助GeoGebra軟件與信息技術(shù)實(shí)驗(yàn)?zāi)M，經(jīng)過反復(fù)模擬與動(dòng)手操作驗(yàn)證，可以對拋物線作圖裝置（圖8）進(jìn)行改裝，從而得到一種多功能圓錐曲線作圖裝置，如圖14所示.

<＼＼10.1.5.160＼g＼中數(shù)高中2024年飛翔＼中數(shù)高中2024年第1期＼圖片13.jpg>[圖14? SolidWorks2012三維立體修改圖]

改裝方法為：將桿a和桿b改為電動(dòng)伸縮桿，通過改變電動(dòng)伸縮桿a，b的長度控制[ab]的值，從而可以作出拋物線、橢圓、雙曲線和圓的圖象.

筆者將這種多功能圓錐曲線作圖裝置命名為“圓錐曲線規(guī)”.

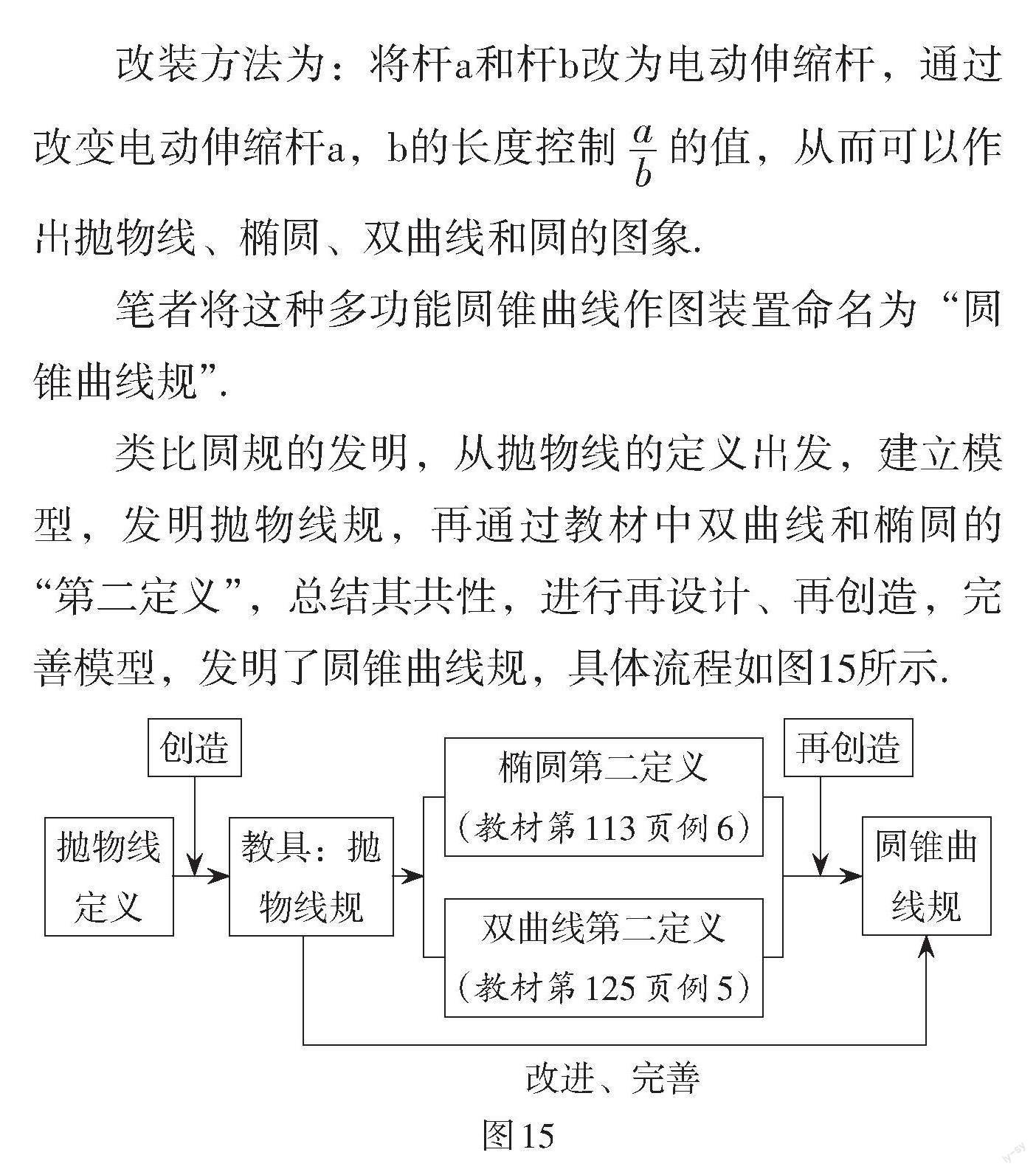
類比圓規(guī)的發(fā)明，從拋物線的定義出發(fā)，建立模型，發(fā)明拋物線規(guī)，再通過教材中雙曲線和橢圓的“第二定義”，總結(jié)其共性，進(jìn)行再設(shè)計(jì)、再創(chuàng)造，完善模型，發(fā)明了圓錐曲線規(guī)，具體流程如圖15所示.

在圓錐曲線內(nèi)容的教學(xué)中，筆者利用圓錐曲線的不同定義，引導(dǎo)學(xué)生抓住其本質(zhì)，抽象出不同的數(shù)學(xué)模型，給出不同的教具設(shè)計(jì)方案，進(jìn)行教具創(chuàng)新實(shí)驗(yàn)，培養(yǎng)了學(xué)生的創(chuàng)新思維和實(shí)踐能力，促進(jìn)了學(xué)生對知識(shí)的深入理解，提高了學(xué)生的數(shù)學(xué)建模和數(shù)學(xué)抽象等素養(yǎng). 同時(shí)，模型的抽象與實(shí)物化，讓學(xué)生掌握了教具設(shè)計(jì)和制作的一般方法，為以后設(shè)計(jì)其他數(shù)學(xué)教具提供了參考，培養(yǎng)了學(xué)生的科學(xué)精神.

參考文獻(xiàn)：

［1］李兆新. 讓“自制教具”重回高中數(shù)學(xué)課堂［J］. 數(shù)學(xué)教學(xué)通訊，2020（36）：81，86.

［2］趙爽. 一種圓錐曲線展示裝置：2019211690-

34.8［P］. 2020-05-19.

［3］孫新波. 發(fā)揮自制教具在高中數(shù)學(xué)新課程實(shí)施中的作用［J］. 中國教育技術(shù)裝備，2014（5）：126-127.

［4］朱婷婷，朱潤，孫家和，等. 一種高中數(shù)學(xué)多功能拋物線作圖裝置：202120398291.X［P］. 2022-02-18.

［5］王少楠. 一種圓錐曲線規(guī)及其使用方法：202110617307.6［P］. 2021-07-30.