條條大路通羅馬，“佳徑”只怕有心人

劉宣妍

在小區里生活，我們就不可避免要到小區的公交站、垃圾站、菜市場、小賣部等地點完成一系列的生活行為。如果路線規劃不當，容易走“冤枉路”和“回頭路”。節假日期間，我運用學習的平面幾何知識，以我所生活的小區為例，探索了小區日常生活中的“最佳路徑”，下面與小伙伴們共享。

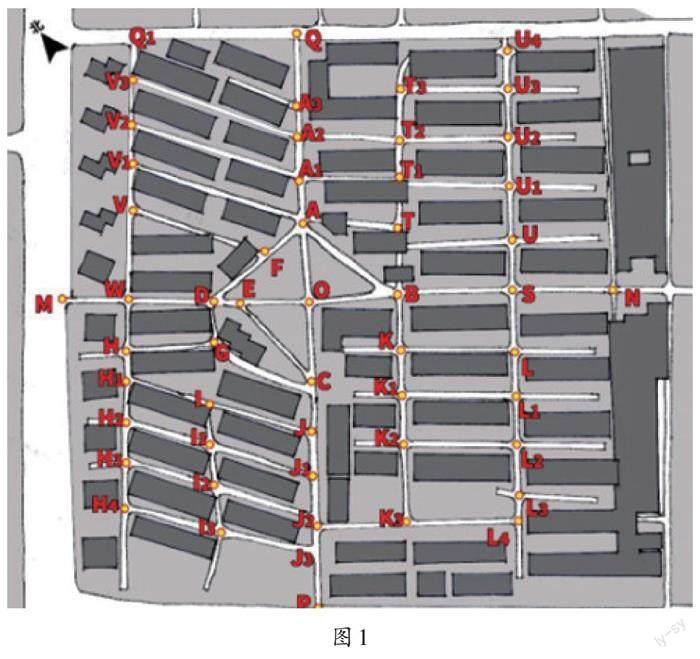
如圖1所示，小區內部道路網可以等價看作若干條線段相連而成，每條道路以及交匯點分別用英文字母表示。若現在需要從小區的M、Q1這兩個入口出發，完成取快遞（到達A點）、買水果（到達F點）、買面包（到達B點）等一系列行為，最終回到家中（到達K點），該如何選擇路程比較短的路徑呢？我試著列出一些路徑進行比較，盡量不包含折返和逆向路徑。

1.從M點出發，我列的路徑如下：

（1）MW→WV→VF→FA→AB→BK；

（2）MW→WV1→V1A→AF→FD→DB

→BK；

（3）MW→WV2→V2A1→A1A→AF→FD→DB→BK；

（4）MW→WV3→V3A2→A2A→AF→FD→DB→BK；

（5）MW→WD→DF→FA→AB→BK；

（6）MW→WH→HG→GD→DF→FA

→AB→BK；

（7）MW→WH1→H1I→IJ→JC→CG→GD→DF→FA→AB→BK；

（8）MW→WH2→H2I1→I1J1→J1C→CG→GD→DF→FA→AB→BK；

（9）MW→WH3→H3I2→I2J2→J2C→CG→GD→DF→FA→AB→BK；

（10）MW→WH4→H4I3→I3J3→J3C→

CG→GD→DF→FA→AB→BK。

2.從Q1點出發，我列的路徑如下：

（11）Q1W→WD→DF→FA→AB→BK；

（12）Q1V→VF→FA→AB→BK；

（13）Q1V3→V3A2→A2A→AF→FD→

DB→BK；

（14）Q1V2→V2A1→A1A→AF→FD→

DB→BK；

（15）Q1V1→V1A→AF→FD→DB→BK。

隨后，我利用所學的幾何知識對我所列的這些路徑進行篩選。可以明顯看出，（2）（3）（4）較（1）復雜，且長于（1），可以舍棄。同理，（7）（8）（9）（10）也可以舍棄。又由“兩點之間線段最短”，可知WH+HG+GD＞WD，則（6）舍棄。可以明顯看出，（13）（14）（15）較（12）復雜，且長于（12），可以舍棄；又由“兩點之間線段最短”，可知VW+WD+DF＞VF，則（11）舍棄。

通過比較，我現在得到（1）（5）（12）三條路徑較為合理，我就這些路徑又進行討論。

從M點出發，不難發現，以W點為圓心，WD為半徑，向VW畫弧，可知，VW＞WD。同理，以F點為圓心，DF為半徑，向VF畫弧，可知，VF＞DF，則（1）長于（5），舍棄（1）。

從Q1點出發，也不難發現，以DF為半徑，F點為圓心，向VF畫弧，交VF于點D1，則DF=D1F＜VF。如何比較MD與Q1V的長呢？我利用圓規截取MD線段的長，以該長為半徑，以V點為圓心，向Q1V作弧，弧與Q1V的交點在線段Q1V上，則Q1V＞MD，則路徑（12）長于路徑（5），舍棄（12）。

綜上所述，路徑（5）是“最佳路徑”。

那么，我的這一道路規劃是否合理呢？通過測距軟件進行測距驗證，我發現路徑（5）為272m，路徑（12）為324m，與篩選結果一致。感興趣的小伙伴還可以多列幾條路徑，利用幾何知識進行對比，或者從Q、P、N出發，找找“最佳”路徑哦！

正所謂“留心處處皆學問”，我通過對小區路徑的測算和驗證，發現平面幾何知識的應用能夠為日常生產生活提供更多便利，讓我更加深刻地體會到數學的魅力。這也不免令我感嘆，條條大路通羅馬，“佳徑”只怕有心人。

教師點評

這篇文章中，小作者從日常生活入手，結合平面幾何基本知識，探索居民小區里面的“最佳”路徑，靈活運用數學知識解決實際問題，體現了“數學有用，數學好玩”。希望同學們今后善于用數學的眼光觀察生活，在“做中學”，在“學中做”，實現學以致用，能用數學思維解決生活中的實際問題。

（指導教師：張衛明）