非常規油氣井用套管抗擠毀性能有限元分析*

汪 強，晁利寧，白天嬌，焦 煒，苑清英，楊曉龍，郭 鵬

（1.中油國家石油天然氣管材工程技術研究中心有限公司，西安 710018；2.中國石油寶雞石油鋼管有限責任公司，陜西 寶雞 721008；3.中石油煤層氣有限責任公司 北京物資分公司，北京 102206）

0 前 言

隨著我國石油勘探水平的不斷提高，深井、超深井、熱采井以及高溫高壓氣井的數量逐年增加，地層環境愈來愈復雜，對套管的性能提出了更高的要求。在頁巖氣、致密氣等非常規油氣井開采中，套管的抗外擠性能已成為管柱設計最重要的依據[1-3]。引起套管擠扁、縮徑、錯段、損壞的原因是復雜的，但根本原因是在地層應力作用下套管所受外部載荷超過了套管的抗外壓載荷強度[4]。

通常影響套管抗擠性能的因素主要包括幾何精度、屈服強度、狗腿度等。國內外針對套管抗擠毀強度問題開展了大量的有限元分析[5-8]，但在分析過程中，通常假定鋼級一定且屈服強度均一[9]，未充分考慮屈服強度在管體周向的不均勻對套管抗擠毀強度的影響，且在眾多變化因素中未得出影響抗擠毀強度的主要因素及次要因素。

本研究在國內外有限元分析研究的基礎上，在規格和鋼級確定的條件下，充分考慮套管本體和井下受力情況，針對幾何尺寸缺欠、屈服強度變化等因素，建立有限元模型，并基于弧長法進行套管抗擠毀性能分析，研究均勻外壓作用下，外徑橢圓度、壁厚不均度、屈服強度不均勻分布等因素對套管抗擠毀性能的影響規律。

1 分析方法及模型建立

1.1 數值分析計算

API SPEC 5C3 標準[10]規定，無軸向載荷和內壓作用下，管體最小抗擠毀強度由材料最小屈服應力fymn和管體橫截面幾何尺寸確定。可分為屈服強度擠毀壓力PYp、塑性擠毀壓力Pp、過渡擠毀壓力PT和塑彈性擠毀壓力PE。

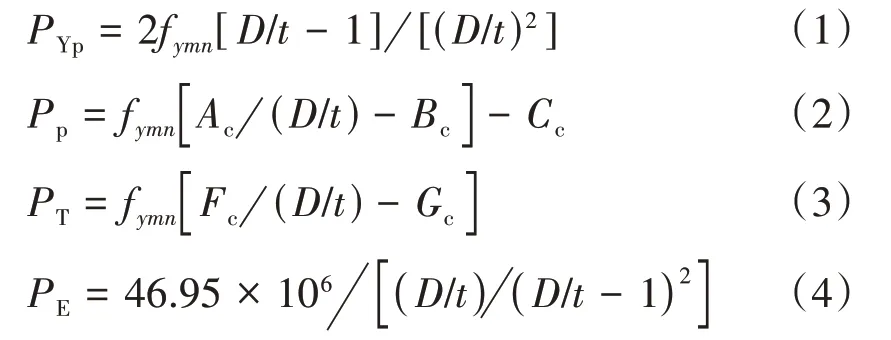
式中：Ac、Bc、Cc、Fc、Gc——計算管體擠毀壓力的經驗系數；

D——管體直徑，mm；

t——管體壁厚，mm。

最小屈服強度擠毀壓力公式（1）適用范圍為（D/t）≤（D/t）yp，最小塑性擠毀壓力公式（2）適用范圍為（D/t)yp≤（D/t）≤（D/t)pt，過渡擠毀壓力公式（3）適用范圍為（D/t）yp≤（D/t）≤（D/t）te，彈性擠毀壓力公式（4）適用范圍為（D/t）te≤（D/t）。以P110 鋼級Φ139.7 mm×10.54 mm 套管為例，D/t=13.25，依照API SPEC 5C3 標準相關規定，確定采用公式（2） 進行套管抗擠毀強度計算，此時Ac取值3.181，Bc取值0.081 9，Cc取值2 852。

1.2 產品條件及因素分析

針對API套管，開展套管抗擠毀性能分析。為確保套管具有優異的抗擠毀性能，通常需對套管的橢圓度、壁厚不均度進行控制。API SPEC 5CT—2018 標準規定了套管的外徑、壁厚及屈服強度范圍，但未對管材的橢圓度和壁厚不均度范圍進行明確規定[11]。本研究在標準要求的基礎上，結合P110 鋼級Φ139.7 mm×10.54 mm套管實際情況，確定了幾何尺寸范圍和力學性能。在有限元計算過程中，屈服強度在API SPEC 5CT—2018 標準要求范圍內間隔取值。幾何尺寸要求見表1，力學性能參數見表2。

表1 P110鋼級Φ139.7 mm×10.54 mm套管幾何尺寸

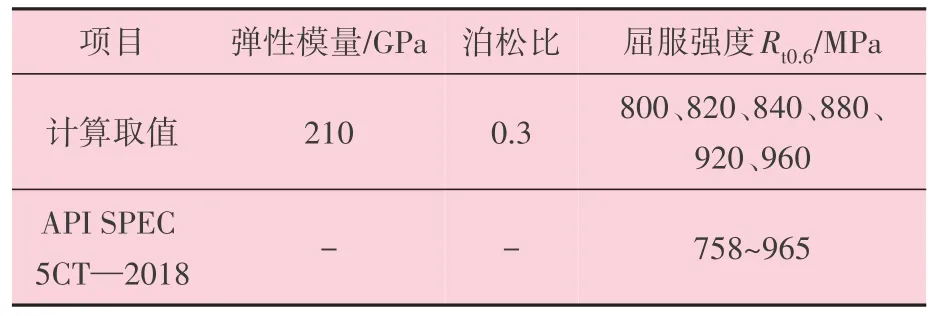
表2 P110鋼級材料性能參數

1.3 有限元分析方法及基本假設

針對表1和表2中的外徑橢圓度、壁厚不均度和屈服強度3個變量因素，進行P110鋼級套管抗擠毀非線性有限元屈曲模擬分析。通過引入弧長因子ΔL，將載荷因子λ和位移增量{ΔU}相聯系，彌補了Newton-Raphson 方法極值點發散的缺點，可以精確求解屈曲載荷[12]。以此分析在API標準要求范圍內，橢圓度、壁厚不均度和屈服強度不均勻分布3個因素對套管抗擠毀強度的影響情況。

1.4 建立模型

根據以上分析條件，假設套管所受外壓沿周向分布均勻，不考慮套管殘余應力影響。建立外徑橢圓度、壁厚不均度和屈服強度變化的二維有限元分析模型。通過轉換公式將試驗所得工程應力-應變曲線轉換為材料的真實應力-應變曲線，相鄰屈服強度對應的材料參數等比例放大/縮小。采用二維平面彈塑性非線性模型進行套管抗擠毀性能分析，利用4節點單元進行網格剖分。建立的有限元幾何模型及網格如圖1所示，網格單元數4 400個。

根據對創業中主要困難的調查，54家樣本科技型創業企業中，有75.93%的企業將融資難、融資貴列在首位，占比最高；同時有超過一半的企業認為政策支持不完善和創新創業能力不足影響企業發展。基于上述現狀與問題分析，要進一步發揮眾籌對科技創業的支持作用，還需強化政策支持，完善風險防控和監管措施，構建長效機制，形成協同效應，打通政策落地“最后一公里”。

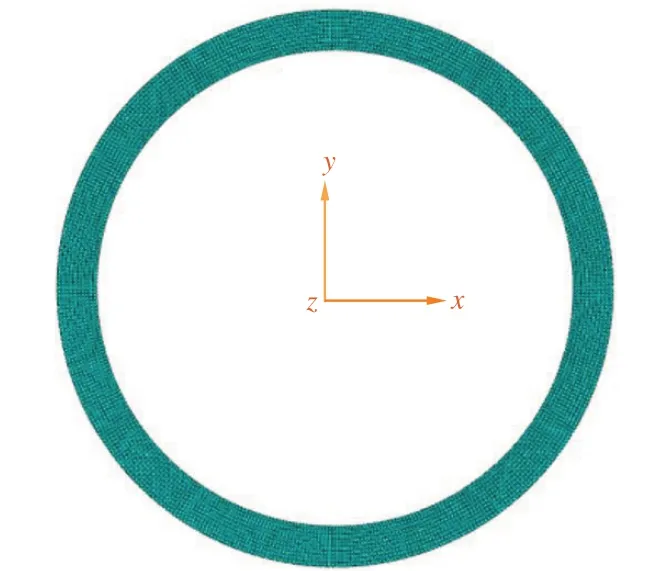
圖1 有限元幾何模型及網格

在設定約束時，將平面沿坐標軸劃分為四個象限，在每個象限邊界處設置約束，確保套管不平移的前提下能夠在外壓作用下沿徑向發生彈性及塑性變形。在管體外徑上施加外壓載荷，載荷線性增加，直至管體發生外壓擠毀。邊界條件及載荷施加情況如圖2所示。

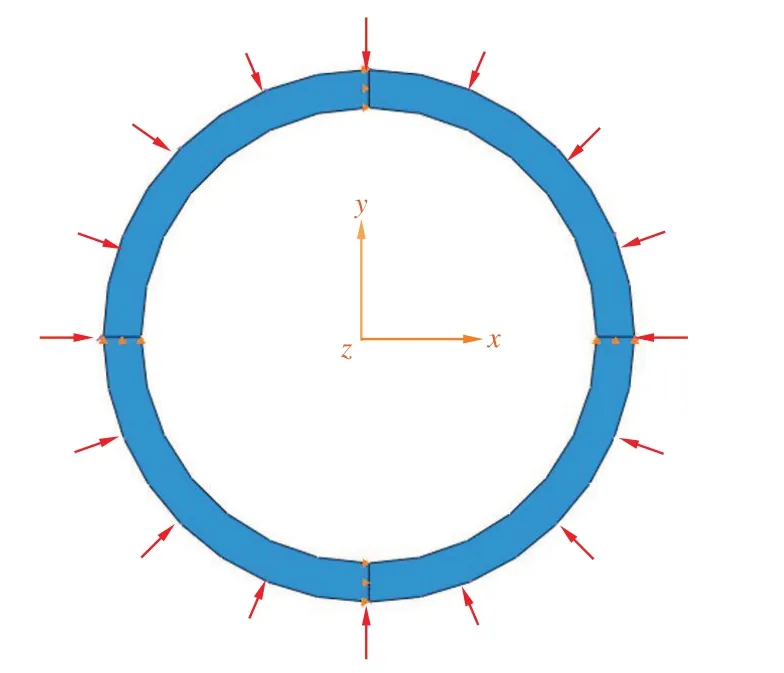
圖2 邊界條件及載荷施加

2 計算結果及分析

套管幾何缺欠主要包括橢圓度和壁厚不均度兩個方面，橢圓度及壁厚不均度又分別由最大外徑、最小外徑、最大壁厚、最小壁厚引起，因而其組合形式多樣，考慮極限情況，通常有8種組合形式，其中壁厚偏差與橢圓外形大徑方向一致時，大外徑+小壁厚組合的抗外壓擠毀強度相對最差，用于抗擠毀性能分析最為穩妥。故在多因素分析過程中，假設幾何缺欠組合形式為壁厚偏差與橢圓外形大徑方向一致，即為大外徑+小壁厚組合[13]。組合形式如圖3所示。

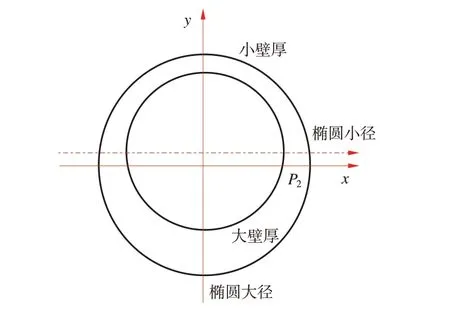
圖3 壁厚偏差與橢圓外徑組合示意圖

2.1 幾何尺寸對抗外壓擠毀強度的影響分析

2.1.1 管體外徑橢圓度對抗外壓擠毀強度的影響

針對橢圓度變化進行套管抗外壓擠毀強度有限元模擬，假設屈服強度沿周向均勻分布。橢圓度依次為0.2%、0.4%、0.6%、0.8%，壁厚不均度設定為2%。橢圓度0.4%時模擬獲得的套管抗擠毀應力云圖如圖4所示，從圖4可以看出，在外壓作用初始階段，套管應力就出現不均勻分布。套管橢圓大徑方向上，套管內側應力高于外側；橢圓小徑方向上，套管外側應力高于內側。外壓作用至擠毀狀態時，套管沿橢圓小徑方向被壓扁。最終，套管完全擠毀，套管內側貼合。模擬過程中，套管承受外壓初期壓力逐漸升高，到達峰值后，迅速降低。三個階段分別對應圖4中的三種應力狀態，峰值壓力即為模擬得到的套管抗擠毀強度。

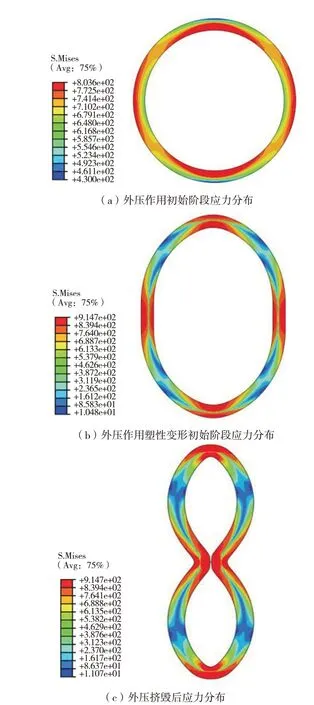
圖4 壁厚不均度2%、橢圓度0.4%套管抗擠毀應力云圖

模擬獲得的套管抗擠毀強度與橢圓度變化關系如圖5所示。從圖5可以得出，隨著橢圓度的增大，套管抗外壓擠毀強度模擬結果逐漸降低。與理論計算結果對比發現，橢圓度較小時的模擬結果遠高于理論計算結果，隨著橢圓度的增大，模擬結果與理論計算結果差值逐漸減小。

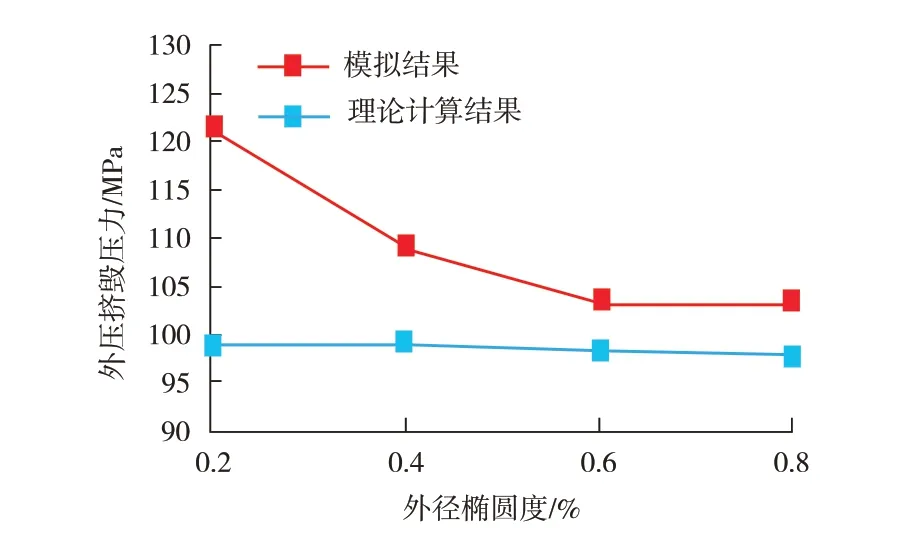
圖5 橢圓度變化時模擬結果與理論計算結果對比

2.1.2 管體壁厚不均度對抗外壓擠毀強度的影響

在模擬分析壁厚不均度變化對套管外壓擠毀強度的影響時，假設屈服強度沿周向均勻分布且套管橢圓度為0.4%。最小壁厚不變，通過最大壁厚增加調整壁厚不均度，壁厚不均度分別為2%、4%、6%、8%。模擬獲得的壁厚不均度變化與套管抗擠毀強度的關系如圖6所示。從圖6可以得出，隨著壁厚不均度的增加，套管的抗外壓擠毀值模擬結果逐漸增大，且均高于理論計算結果。

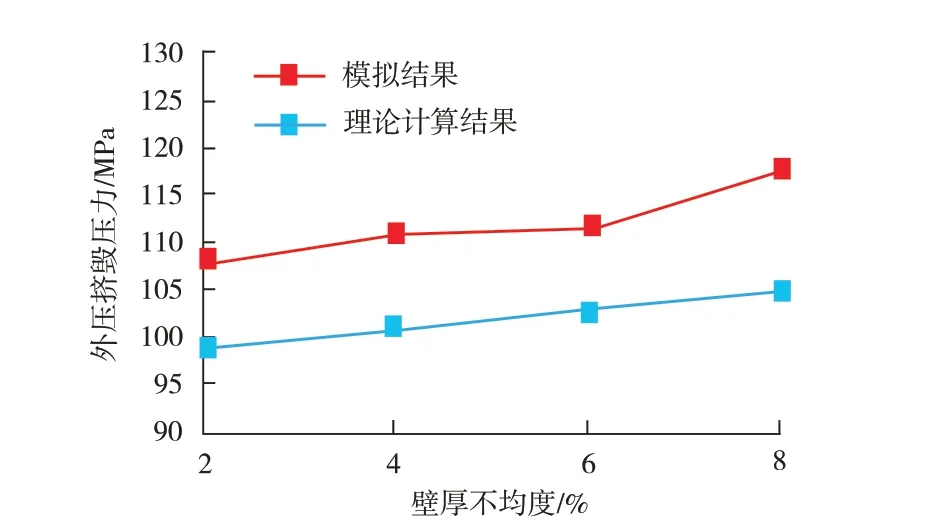
圖6 壁厚不均度變化時外壓擠毀的模擬結果與理論計算結果對比

2.2 屈服強度變化對抗外壓擠毀性能影響分析

2.2.1 屈服強度均勻整體變化

按照API SPEC 5CT 標準，當鋼級一定時套管的屈服強度并不是固定值，而是在一個區間內。為此，研究分析鋼級一定時，屈服強度變化對套管的外壓抗擠毀性能的影響規律。屈服強度分別取800 MPa、820 MPa、840 MPa、880 MPa、920 MPa 和960 MPa，橢圓度為0.4%，壁厚不均度為2%，模擬及理論計算結果如圖7 所示。從圖7可以得出，隨著屈服強度的升高，外壓擠毀模擬結果和理論計算結果均不斷升高，且模擬結果始終高于理論計算結果，但二者間的差值逐漸減小。

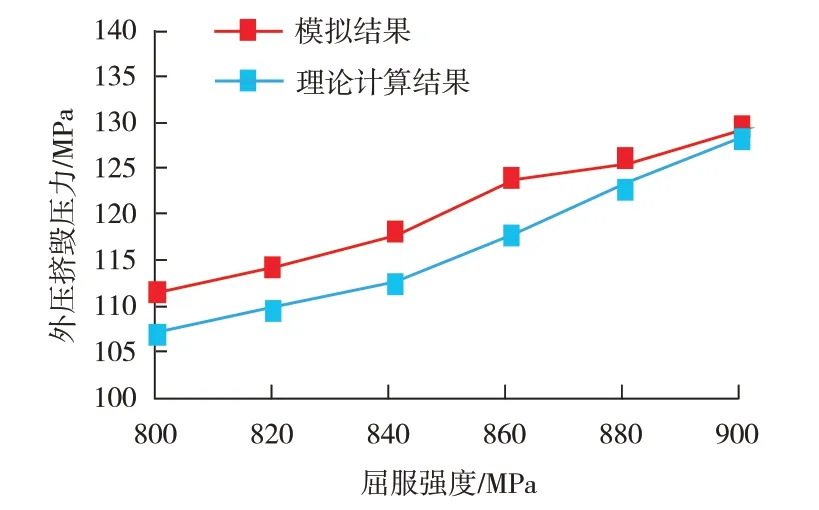
圖7 屈服強度均勻變化時的外壓擠毀模擬及理論計算結果對比

2.2.2 屈服強度分布變化

以上外壓擠毀模擬分析時，均假設管體的屈服強度沿管體周向均勻分布，而實物管體的屈服強度通常沿管體周向是有差異的。為進一步分析屈服強度沿管體周向的不均勻變化對管體外壓擠毀性能的影響規律，將管體沿周向劃分為四個象限，每個象限分別賦予不同的屈服強度，建模時設定橢圓度0.4%、壁厚不均度2%，屈服強度分布見表3（屈服強度分布方案按均勻性優劣依次為：方案4>方案3>方案2>方案1>方案5），四個象限的平均屈服強度相同，建模象限劃分如圖8 所示。

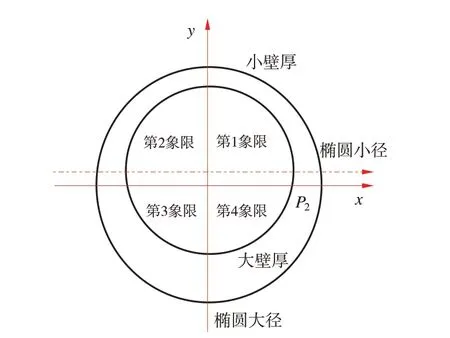
圖8 沿圓周方向四個象限劃分情況

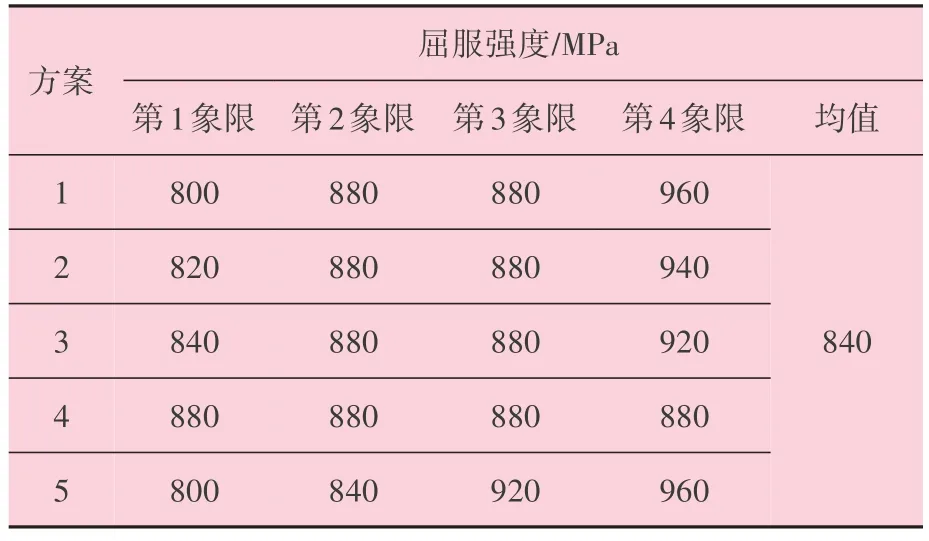
表3 沿圓周方向四個象限屈服強度分布情況

模擬獲得的屈服強度沿周向變化時的外壓擠毀分析結果如圖9 所示，結合表3 分析發現，當平均屈服強度一定時，屈服強度沿管體周向分布越均勻（方案4），套管的抗外壓擠毀強度越高；屈服強度越分散（方案5），抗外壓擠毀強度越低。

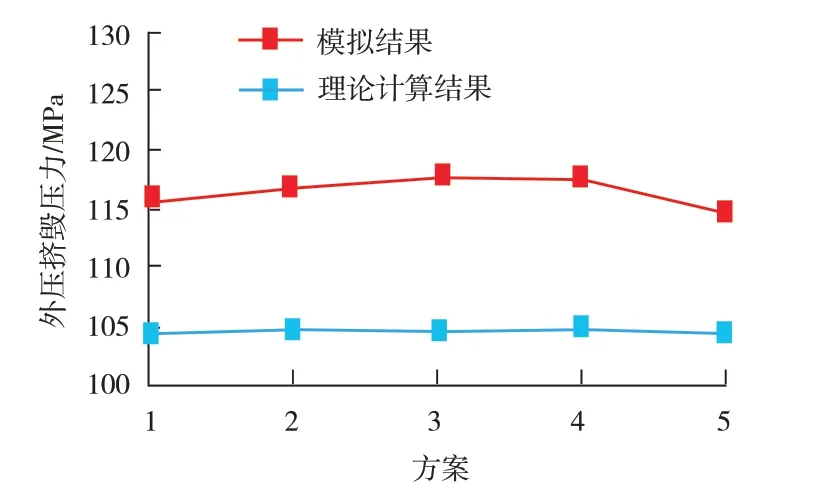
圖9 屈服強度分布變化時的外壓擠毀分析結果

3 實物外壓試驗與有限元分析結果對比

為了驗證模擬分析得出的幾何尺寸缺欠參數對套管外壓擠毀結果影響規律的有效性，對P110 鋼級Φ139.7 mm×10.54 mm 套管進行抗外壓擠毀實物試驗驗證。經測量，該套管實物缺欠幾何尺寸見表4。在此基礎上，試驗檢測了套管實物的屈服強度。檢測屈服強度時，將管體沿橫截面化分為四個象限[14]，在每個象限內取一組拉伸試樣進行試驗，確定每個象限的屈服強度和抗拉強度，屈服強度檢測結果見表5。取樣后，剩余管樣進行外壓擠毀試驗。外壓擠毀試驗方法按照SY/T 6238.1《油井管全尺寸試驗方法 套管擠毀試驗》執行，試樣長度為3.8 m，超過8 倍的外徑長度[15]，試驗過程中以不超過35 MPa/min 的加壓速度升壓，直至套管壓潰。套管實物擠毀試驗曲線如圖10 所示，通過實物試驗得出的套管抗外壓擠毀強度為116.7 MPa，外壓擠毀形貌如圖11所示。

圖10 套管外壓擠毀試驗曲線

圖11 套管外壓擠毀后實物形貌

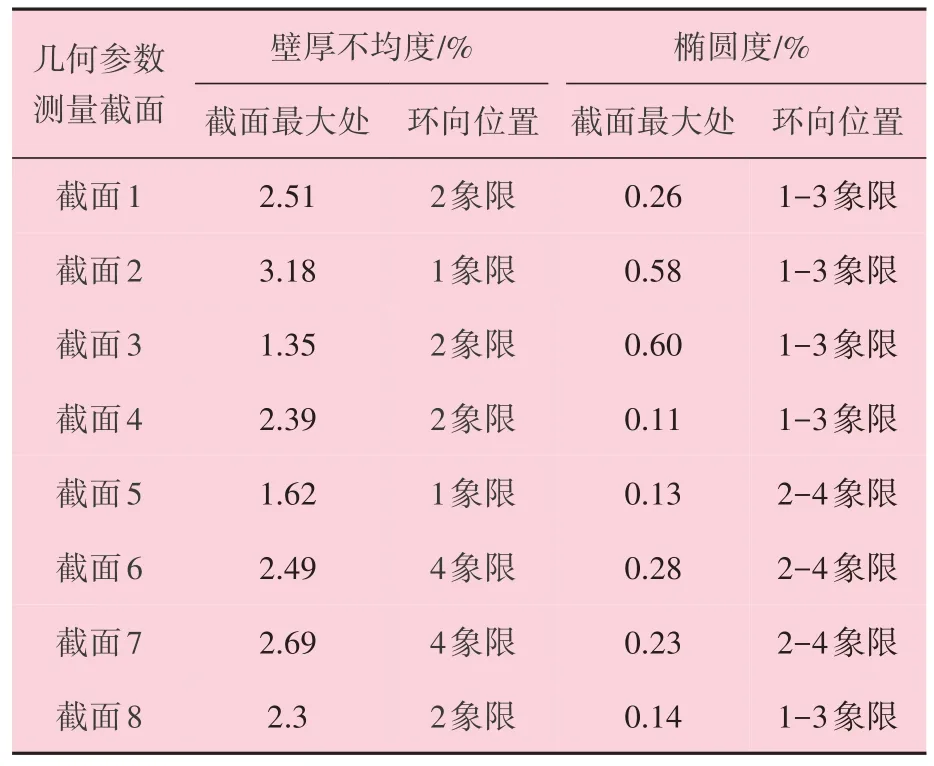
表4 套管外壓擠毀實物試驗缺欠幾何尺寸

表5 套管實物沿圓周方向屈服強度（Rt0.6） MPa

根據模擬得到的幾何尺寸缺欠影響結果可知，橢圓度比壁厚不均度對套管抗擠毀性能影響更大。截面3 位置實測壁厚不均度1.35%是樣管中最小的，對應的橢圓度0.6%是樣管中最大的。截面3 位置先出現變形失效，外壓擠毀強度最小，是最薄弱截面。因此，根據截面3 實測的幾何尺寸參數進行套管抗外壓擠毀性能建模和理論計算，模擬結果得出套管實物擠毀壓力為116.3 MPa，理論計算得出的實物抗外壓擠毀結果為111.6 MPa。

將有限元分析得出的管體抗外壓擠毀強度值與實際試驗套管抗外壓擠毀強度值進行對比，發現通過劃分象限獲取的屈服強度和實測幾何尺寸建模方式模擬得出的外壓擠毀結果與實物試驗結果十分接近，并優于API 理論公式計算的結果，可以更加精確地預測套管實物的外壓擠毀強度。

4 結 論

（1）在尺寸公差要求范圍內，當套管管體幾何形狀存在橢圓度和壁厚不均度缺欠時，橢圓度對套管外壓擠毀性能的影響大于壁厚不均度的影響。

（2）在套管橢圓度和壁厚不均度一定的情況下，隨著屈服強度的均勻升高，外壓擠毀模擬結果和理論計算結果均不斷升高，且模擬得出的外壓擠毀結果始終高于理論計算結果，但二者間的差值逐漸減小。另外，平均屈服強度一定時，管體屈服強度沿周向分布越均勻，套管的抗擠毀性能越好，但均不超過屈服強度均勻時的外壓擠毀結果。

（3）根據模擬得出的幾何尺寸缺欠對套管外壓擠毀試驗結果的影響規律，實測套管橫截面的橢圓度、壁厚不均度兩種幾何尺寸缺欠，找出套管實物最薄弱截面。通過分象限實測屈服強度和實測幾何尺寸相結合的建模方式，可以更加精確地預測套管實物的外壓擠毀強度，通過開展驗證試驗，對比理論分析的數值模擬結果與試驗測試結果，進一步驗證了數值建模方法的合理性。