西北江徑流量變化對感潮河口咸潮上溯的影響

梁靖習, 徐龑文*, 張蔚, 周榮香

(1. 河海大學水災害防御全國重點實驗室, 南京 210024; 2. 河海大學港口海岸與近海工程學院, 南京 210024; 3. 湖南省交通規劃勘察設計院有限公司, 長沙 410000)

河口承擔著連接河流與海洋的作用,沿海地區的農業、工業及生活用水均來自于河口[1-4]。然而,咸潮的上溯會污染水質,致使水體無法滿足人們的生產生活需要。因此,河口地區的咸潮上溯問題受到了學者們的密切關注[5-9]。咸潮的上溯距離是河口生態環境的關鍵指標,考慮到復雜多變的地理條件與水文因素,咸潮的上溯距離在各種情況下不盡相同。近年來,學者們嘗試利用求解半經驗模型的方法來預測咸潮上溯的距離[10-13]。Brockway等[14]在簡化條件下解析求解了鹽度對流擴散方程,得出Incomati河口處咸潮上溯的最遠距離,考慮到該河口的部分特征可以用指數函數描繪,他們修改了Savenije[9]和Prandle[15]所提出的結論并提出了全新的公式,這些半經驗公式基于參數縮放與現場觀測,具有較為廣泛的實用性,并且只需要輸入較少的數據,形式簡潔,操作方便。以往這些半經驗公式多應用于水動力條件相對簡單的河口(如Hudson河口和Arvand河口[16])。然而在水動力條件較為復雜的河口(如中國珠江流域磨刀門河口),目前未做解析分析的相關探究。磨刀門河口的咸情需要進一步的研究。21世紀以來,由于河道疏浚、人工挖沙以及氣候條件等原因,咸潮災害頻繁發生,區域供水形勢十分嚴峻。為應對咸潮上溯問題,生產實踐總結了“偷、引、蓄、截、擋、壓”等技術方法[17-18]。因此,河口咸水界(即咸潮上溯距離)的準確預測可為取水口優化布置提供重要技術支撐。在解析對流擴散方程的基礎上,結合數值模擬法,分析磨刀門咸潮上溯隨上游徑流變化規律,提出咸潮上溯距離與徑流響應模型,通過半經驗模型的比較研究,探討不同模型在磨刀門咸潮上溯距離預測中的異同特點,確定磨刀門咸潮上溯的最優預測模型,以期降低磨刀門咸潮上溯距離預測的成本并提高預測精度。

1 數學模型

1.1 模型簡介

模型采用隱式有限差分法,水動力模塊基本方程采用圣維南方程組,鹽度模塊采用對流擴散方程[19]。模型的上游邊界采用2001 年枯季石嘴(潭江)、高要(西江)、石角(北江)、老鴨崗(廣州上游)和博羅(東江)的實測流量數據,外海邊界設置在珠江口外南海-30 m等深線附近,下邊界潮汐使用 TPXO8(TOPEX/POSEIDON)全球大洋潮汐模式得到的潮時間序列。根據統計資料,模型在從陸地到外海的開邊界鹽度值為20‰～33‰。計算網格考慮選擇矩形網格和三角形網格相結合,在順直平滑的河道中使用矩形網格,在外海為了更貼合岸線則采用三角形網格。在本模型里,給定了全河網區一個全局曼寧值0.025。曼寧系數從口門至上游逐漸增大,北江干流(石角-三水)為0.026～0.045,西江河道(高要-百頃頭)為0.020～0.028,磨刀門水道(百頃頭-燈籠山)為0.016～0.022,伶仃洋內部平均為0.016。

1.2 模型驗證

在驗證過程中,為了定量評估驗證精度與合理性引入了統計指標SS(skill score)。SS指標表達式如式(1)所示。模型驗證包括水位、流量與鹽度的驗證,采用2001 年2 月7 日—16 日的實際潮位、流量與鹽度數據,數據間隔時間為1 h。圖1、圖2 與圖3 所示為模型水位、流量與鹽度的驗證圖。

圖1 潮位驗證圖Fig.1 Validation of tidal level process

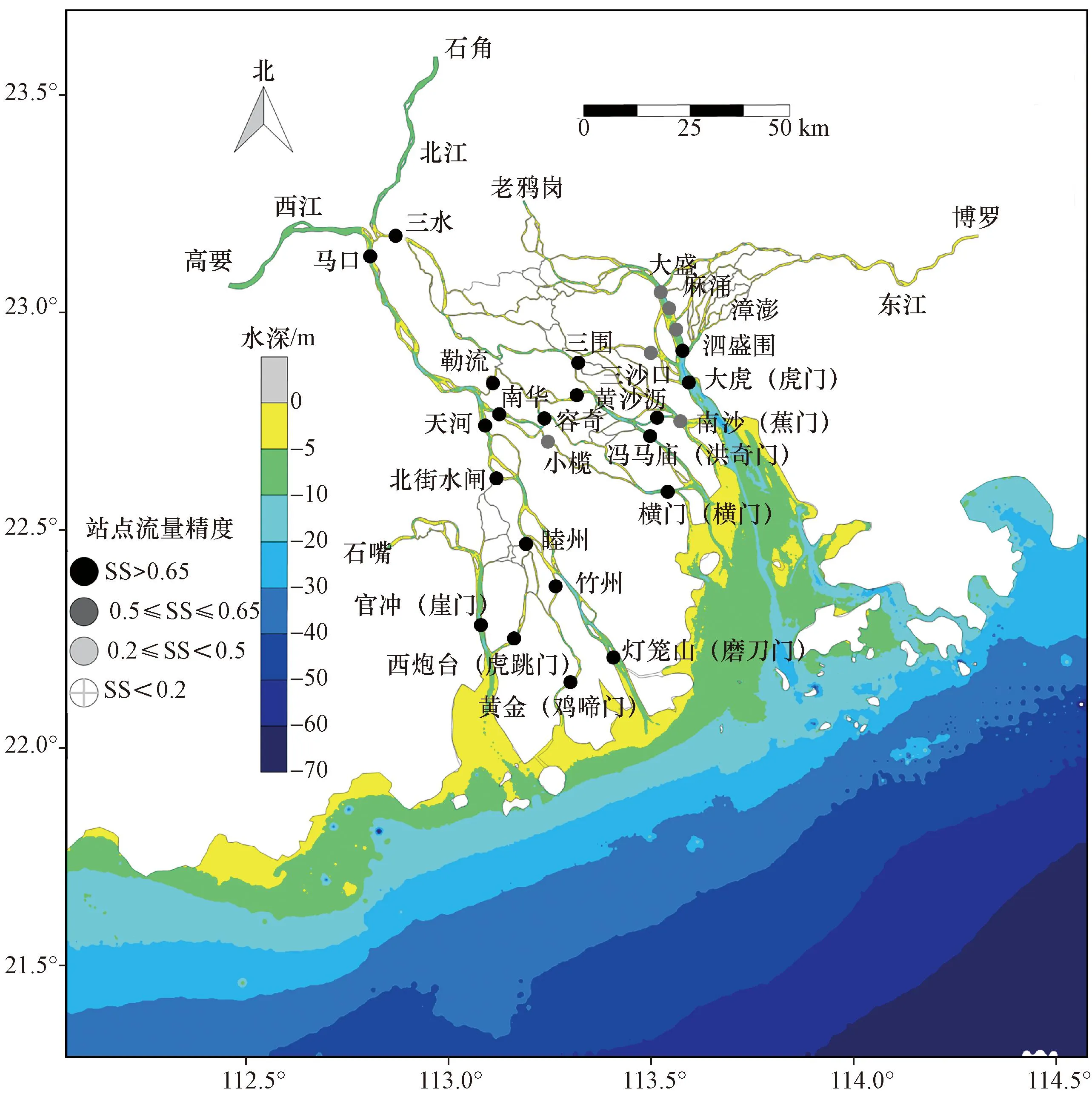
圖2 流量驗證圖Fig.2 Validation of discharge

(1)

式(1)中:SS為模型精度檢驗指標;Xmol,i為模型計算值;Xobs,i為實測數值;Xobs為實測值的平均值。判斷標準為:SS<0.20 時為不合格;0.20≤SS<0.50 時為合格;0.50≤SS≤0.65 時為良好;SS>0.65 時為優秀。

由圖1～圖3可知,大部分站點水位、流量SS值均大于0.65,水位和流量的驗證結果較好。除東四口門部分上游站點(如容奇、大盛和三圍)鹽度SS為0.5～0.65 外,其余大部分站點鹽度驗證結果良好。總體而言,本模型能較好地反映鹽度的整體分布,可信度較高。

2 上溯距離對徑流響應的理論公式

2.1 理論關系推導

一般來說,咸潮上溯過程是河流淡水與海中咸水進行水體交換的過程,河流中的淡水趨向于將鹽分帶出河口,降低水體的鹽度,海水趨向于將鹽分向上游輸送。當河口處于穩定狀態時,二者相互平衡,此時河口鹽度平衡過程可用鹽度對流擴散方程表示為

(2)

式(2)中:A為河口斷面面積;x為站點距離口門的距離;S為鹽度;Q為流量;Dx為鹽度縱向對流擴散系數;t為時間。當河口鹽度處于平衡狀態時,不考慮時間效應,則式(2)可忽略時間項,兩邊積分得到穩態函數

(3)

縱向擴散系數Dx涵括了河口咸潮上溯的不同動力機制,是模型中最重要的參數之一。基于重力環流解析模型,Fischer[20]和Monismith等[21]指出,假設密度驅動擴散橫向作用主導,可得鹽度擴散系數的解析表達為

(4)

式(4)中:α′為比例常數;β′為鹽度膨脹率;H為水深;υt為動量渦流擴散系數,將式(4)代入式(3)得

(5)

式(5)中:W為河口寬度,斷面面積A為河口寬度W與河口水深H的乘積。因此,基于式(5),根據咸潮上溯距離空間尺度,確定咸潮上溯距離與徑流的關系可表示為

(6)

式(6)中:L為咸潮上溯距離。從式(6)中可以看出,對于理想河口,咸潮上溯距離與上游徑流量呈現冪律函數關系,其冪指數理論值為-1/3。然而,根據大量實測河口數據分析表明,該冪指數與河口流量密切相關,其值在0～-1之間變化。Maccready[22]研究表明,對于小流量河口,即潮控河口,其咸潮上溯對徑流的依賴性較弱,流量越小,冪指數取值越接近于0;對于大流量河口,即徑控河口,其咸潮上溯對徑流的依賴性較強,流量越大,冪指數取值越接近于-1。因此,河口咸潮上溯距離和徑流響應的理論關系函數表達式可寫為

L=αQβ

(7)

式(7)中:α為河口特征影響系數,與河口形態特征及動力特征有關;β為徑流響應系數,與河口上游徑流強弱相關。響應模型的兩個控制系數可通過實際河口的徑、潮動力及鹽度數據確定。

2.2 半經驗模型公式

本文中選取了幾種較為常用的半經驗模型,結合珠江口實測數據,構建磨刀門咸潮上溯距離的快速預測模型。這些半經驗模型基于物理實驗及現場觀測方法構建,對實測數據的依懶性較弱,只需少量河口水文及地形數據即可開展咸潮上溯研究,因此,在世界范圍內已有較為廣泛的應用[7-10]。

Rigter[11]利用水槽模型實驗,得到咸潮上溯距離的經驗關系為

(8)

(9)

(10)

(11)

式中:LLWS為落憩咸潮上溯距離;h0為潮平均水深;f為達西系數;Fd為密度弗勞德數;R為河道橫斷面的水力半徑;F為弗勞德數;ρ為水體密度;v0為潮汐流速振幅;Δρ為鹽淡水的密度差;N為坎特·克里默斯數,其計算公式為

(12)

式(12)中:Q為徑流量;T為潮周期;Pt為潮通量;A0為口門的斷面面積;u0為口門處的徑流流速;E0為潮程,定義為一個水質點落潮過程或漲潮過程中所運動的距離。

Fischer[12]分析了Rigter[11]收集的數據,重新調整了其中各項系數的指數,提出了公式

(13)

Van 等[13]提出了一個和Rigter[11]類似的公式,即

(14)

Savenije[9]在早期工作的基礎上,利用現場觀測的方法,提出了對于非恒定水深河口咸潮上溯距離預測公式,即

(15)

(16)

式中:LHWS為漲憩時刻咸潮上溯距離;a為河口的斷面收斂長度;D0為口門處的擴散系數;K為Van den Burgh系數。

3 咸潮與徑流的響應特征

根據多年枯季實測流量的統計分析結果,模型取用高要、石角、博羅站多年枯季平均流量的0.5、0.75、1.0、1.25、1.5、1.75、2.0、2.25倍流量作為模型上邊界,進行敏感性實驗(表1)。外海開邊界潮汐潮位為使用TPXO8全球大洋潮汐模式得到的潮位時間序列,取用2001年2月7日16:00—2月24日8:00共400 h潮位過程。模型計算結果如圖4所示,在不同的流量動力組合下,咸界均呈現S形分布特征。珠江三角洲咸潮上溯范圍隨流量的變化而發生顯著變化,且存在一定的空間差異性,咸界在西四口門的變化幅度較大,而東四口門的變化范圍較小。隨著上游徑流的增加,磨刀門水道的咸潮上溯距離明顯減小。當流量達到約5 000 m3/s時,咸潮退至平崗泵站以及南鎮水廠以下。

表1 敏感性實驗上游各站點流量Table 1 Discharges at each station in sensitivity experiment

圖4 不同徑流條件下珠江河口鹽度為0.5‰的咸界Fig.4 Salinity line of 0.5‰ under different discharge conditions

基于河口咸潮上溯距離和徑流的響應關系函數[式(7)],結合數值模擬結果,通過最小二乘法進行擬合率定,可確定磨刀門河口特征影響系數和徑流響應系數。如圖5所示,磨刀門河口特征影響系數為23 332,其徑流響應系數為-0.85,因而,磨刀門咸潮上溯與徑流響應關系為

圖5 咸潮上溯距離與徑流響應關系Fig.5 Relationship between river discharge and salt intrusion length

L=23 332Q-0.85

(17)

式(17)中:L為磨刀門咸潮上溯距離,即口門至0.5‰鹽度值所到處的距離;Q為上游(高要站和石角站)流量值。如圖5所示,對于磨刀門河口來說,咸潮的上溯距離隨著流量的減小而增加,且遵循指數函數關系,隨著上游流量的增加,咸潮的上溯距離逐漸趨于穩定。本研究收集了2007、2009、2010、2012、2013年[23]6組實測水文、鹽度數據(表2),以及Gong等[24]發表的咸潮上溯數值計算數據,對該咸潮與徑流響應模型(L-Q)[式(17)]準確性進行驗證,結果如圖6所示。采用均方根誤差(root mean squared error,RMSE)定量評價響應模型值和實測值之間的差異,RMSE的表達式為

表2 實測水文數據Table 2 Measured hydrological data

圖6 咸潮與徑流響應模型驗證結果Fig.6 Validation of relationship between river discharge and salt intrusion length

(18)

式(18)中:n為總數據數;pi為徑流-咸潮響應模型的計算咸潮上溯值;oi為實測咸潮上溯值。如表2第4列結果所示,基于實測數據比較分析的RMSE值較小,表明該咸潮與徑流響應模型可較好地反演咸潮上溯與徑流的動力關系。

4 半經驗模型適用程度

本文將五種不同的半經驗模型公式應用于磨刀門咸潮上溯距離快速預測研究中,通過比較分析,確定不同方法在磨刀門的適用性。表3展示了模型公式中各項物理量參數在磨刀門的取值。將表3中的參數值代入至上述各半經驗模型公式中,即可應用模型確定變化流量下磨刀門咸潮上溯距離的預測值,不同模型計算值如表4所示。

表3 磨刀門河道各項系數取值Table 3 Values of various coefficients in Modaomen estuary

表4 不同水文條件下咸潮的上溯距離Table 4 Salt intrusion length under different hydrological conditions

如圖7所示,咸潮的上溯距離隨著徑流量的增大而減小。相較實測數據對徑流變化的響應敏感性,Rigter模型和Van模型出現顯著的高估,而Fischer模型則出現顯著的低估,此規律主要受經驗模型中的徑流響應系數(即徑流量Q的冪值)的影響。該系數在Rigter模型和V. Os模型中為-1,在L-Q

圖7 不同半經驗模型咸潮上溯距離預測結果Fig.7 Salt intrusion length of different semi-empirical models

模型中為-0.85,在Ficsher模型中為-0.25,表明冪值越趨近-1,咸潮上溯對徑流量變化的響應越敏感。這一結論與Gong[24]的研究發現相一致。

如圖7所示,Rigter模型、Fisher模型和V. Os模型結果與實測數據比較,誤差較大。這三種半經驗模型公式是基于水槽物理模型實驗確定,未考慮較大尺度河口實際的地形和水動力特征,因此在復雜河口應用時可能會產生較大的偏差。由圖7可知,Savenjie模型和L-Q模型應用在磨刀門均表現得較為出色,Xu等[25]指出是因為兩種模型完善了實驗室模型未考慮天然河口特征的不足。其中,Savenjie模型基于對鹽度流擴散方程推導,提出更符合實際的假設條件,例如,與其他半經驗模型基于河口橫截面恒定不變的假設不同,Savenjie模型中的河口斷面依據河口特征假設為沿程指數變化。而磨刀門L-Q模型則是通過咸潮與徑流響應理論關系,結合磨刀門咸潮上溯實測響應變化規律構建,因此L-Q模型涵蓋的實測河口因素亦較為全面。兩種模型的應用各有優勢,Savenjie模型通過數學推導能夠反映參數之間的物理關系,更適用于河口咸潮上溯機理的分析;而L-Q模型的應用構建只需確定兩個參數,計算效率較高,更適用于河口咸潮上溯距離與壓咸流量快速預測等場景。

綜上,半經驗模型可通過簡單數學公式直接將輸出量(咸潮上溯距離)與控制參數(流量等)相聯系,且在實際應用過程中不需大量的實測數據支撐即可獲取較好的預測結果。因此,將半經驗模型應用于磨刀門咸潮上溯距離計算時,能以較低的時間和金錢成本獲取較高精度預測結果。

5 結論

河口咸潮上溯數學模型需要大量的實測水文和地形數據構建,而利用求解半經驗模型進行咸潮上溯距離計算所需的時間成本和數據成本較低,因而更為直接、便捷。從一維鹽度對流擴散方程出發,結合數值模擬與數學解析方法,構建了磨刀門河口咸潮上溯與徑流響應模型(L-Q模型),并與其他不同半經驗模型的適用特征進行比較分析,結果表明:

(1) 在不同的流量動力組合下,咸界呈現S形分布特征。咸潮上溯距離L與上游徑流量Q在理論上呈現冪指函數關系:L-αQβ,α的取值與河口形態特征及河口動力特征有關,β的取值與河口上流徑流強弱有關,β越趨近-1,咸潮上溯距離對徑流量的變化響應越敏感。

(2) Riger模型、Fisher模型與V. Os模型基于水槽實驗結果構建,在沖積型河口磨刀門的適用性較差。Savenije模型和L-Q模型在磨刀門咸潮上溯距離預測中的應用效果較好,這是由于兩種模型均較好地考慮了實際河口地形和動力特征的影響。

(3) 利用半經驗模型預測磨刀門咸潮的上溯距離是可行的,半經驗公式需要的時間成本與金錢成本較低,并且需要的實測數據量較小。通過比較分析五種半經驗模型公式的應用特征,可知磨刀門咸潮與徑流(L-Q)響應模型使用簡單便捷,計算精度較高,在磨刀門地區適用性較強。