干擾情形下重復性項目快速修復策略模型與算法

王浩, 張立輝, 周琳, 郭欣雨

(華北電力大學經濟與管理學院, 北京 102206)

重復性項目是指所有活動在各個單位之間重復進行的項目,典型的重復性項目包括高層建筑、高速公路和跨海大橋的建設等。很多關于重復性項目調度的研究假設活動持續時間和材料供應是預先知道的并且不會改變[1-5]。然而,Viles 等[6]指出重復性項目是在動態環境中進行的復雜項目,通常會因為極端天氣環境、不利地質條件、政策變化等干擾事件的影響導致項目成本增加,工期延長,甚至導致基準調度計劃不可行。例如:中國的港珠澳大橋項目和美國的波士頓隧道項目均因為復雜的地質條件、惡劣的天氣和資金缺口等干擾事件影響導致工期的延誤和成本的超支。由于重復性項目是建筑行業項目中相當重要的一部分[7],因此有必要研究不確定環境中的重復性項目調度問題。

近年來,為了解決不確定環境下的項目調度問題,學者們提出了三種調度方法,分別為隨機性調度方法、模糊性調度方法和魯棒性調度方法。魯棒性是指調度計劃維持有效性,抵抗干擾事件的能力[8]。與隨機性調度方法和模糊性調度方法相比,魯棒性調度方法對于干擾事件采取了根本性的處理策略,因此該方法成為了解決不確定環境下項目調度問題最具潛力的方法[9]。魯棒性調度方法按照應對干擾事件的處理方法不同又可細分為前攝性調度和反應性調度[9-10]。

前攝性調度是在項目計劃階段,通過插入時間緩沖的方式創建一個具有一定魯棒性的基準調度計劃。許多學者對前攝性調度進行了深入研究,但工程實際表明,即使基準調度計劃具有非常高的魯棒性,也不能完全規避項目執行過程中發生的干擾事件[10]。

反應性調度是在干擾事件發生后,對尚未開始的活動進行重新調整和優化,使反應性調度成本最小。目前反應性調度相關研究主要集中于一般性項目。Deblaere等[11]對多模式資源受限項目反應性調度問題進行研究,旨在資源或活動工期中斷時獲得最小化調度成本的反應性調度計劃。Chakrabortty等[12]進一步考慮了優先關系變化、新活動增加等中斷事件下的反應性調度問題。Elloumi等[13]針對多模式資源受限項目反應性調度問題提出了三種啟發式算法進行求解。彭良武等[14]設計了兩階段多模式反應性調度模型,提高了反應性調度計劃的魯棒性。曹芳芳等[15]認為部分項目不需要滿足鐵路調度規則,活動執行時間可以提前,設計了一種多模式反應性調度模型,進一步降低了反應性調度成本。

與一般性項目相比,重復性項目由于多單元、工作連續性等特點,其反應性調度具備特殊性和復雜性:重復性項目活動受到干擾事件影響時,其緊前活動的部分單元可能尚未開始,因此也可以參與反應性調度;重復性項目可以通過打斷工作連續性(間斷)的方式有效縮短項目工期[16-18],因此除了現有研究常用的改變執行模式手段外,允許活動間斷也可以作為一種重復性項目反應性調度手段。同時考慮改變執行模式和允許間斷兩種手段可以為項目管理者在制定反應性調度計劃時提供更大的靈活性,進而可以得到反應性調度成本更低的調度計劃。

重復性項目的反應性調度研究尚處于起步階段,研究者較少。Sawomir等[19]通過加班和增加資源的方式加快施工,建立成本最小的反應性線性規劃模型。Hegazy等[20]使用軟邏輯和多模式手段修改調度計劃,旨在以最小的成本滿足項目截止日期約束,但該研究沒有闡述重復性項目反應性調度模型。

上述反應性調度相關研究采用的均是完全重調度策略,即針對干擾事件,對尚未開始的所有活動進行全局優化調整。重調度策略能夠實現反應性調度成本最低,但是對整個項目的調整范圍較大,可能不被項目管理者接受。事實上,反應性調度還存在另外一種常被忽略的調整策略——快速修復策略。快速修復策略是指在干擾事件發生后,對尚未開始的活動進行局部優化,使擾動范圍最小并適當兼顧減少反應性調度成本。快速修復策略在項目實踐中非常實用。首先,由于需要調整的活動數量較少,因此對項目的擾動較小,這有利于降低管理和協調難度。尤其是在由多個分包商建造的項目中,快速修復策略可以幫助管理人員減少與其他分包商變更協議的次數;其次,調度計劃的迅速恢復將有效減小項目里程碑延誤的風險,這有利于承包商及時收到里程碑支付款項;最后,調整后的調度計劃偏離基準調度計劃的程度低,因此可以最大程度地保持基準調度計劃考慮的項目目標(工期、魯棒性和資源均衡等)。

綜上所述,目前針對重復性項目反應性調度的研究極少,且尚未有人開展反應性調度快速修復策略的研究。由于關鍵路徑法等傳統調度方法在應對重復性項目調度問題存在諸多問題[4,21],現以在重復性項目中廣泛使用的RSM(repetitive scheduling method)技術為工具,研究重復性項目快速修復調度問題。創新點主要體現在以下三個方面:①首次研究重復性項目快速修復策略,為項目管理者應對干擾事件提供多種修復范圍下的反應性調度計劃;②綜合考慮多模式和間斷兩種反應性調度手段,構建了反應性調度成本-修復范圍權衡優化模型;③針對問題模型,設計了一種基于強化學習的遺傳算法進行求解。

1 模型構建

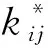
本文中研究的問題可界定如下:在重復性項目執行階段,某一活動受到干擾事件影響而發生延誤時,采用改變執行模式和允許間斷的手段對基準調度計劃進行調整和再次優化,以實現反應性調整范圍和成本最小化的目標。

1.1 目標函數

在實際項目調度過程中,減少反應性調度成本是項目管理者最重視的目標之一,同時快速修復是管理者的現實需求。

本文提出的反應性調度優化模型的第一個目標函數是最小化反應性調度成本。表達式為

minCT=Cdc+Cmsdc+Cia+Cmsmc

(1)

式(1)中:CT為反應性調度成本,由偏差成本Cdc、模式更改帶來的額外直接成本Cmsdc、項目工期變化而引起的額外間接成本Cia與更改活動執行模式和開始時間而引起的一次性額外調整成本Cmsmc組成。

(2)

(3)

式(3)中:Cmsdc為由于活動執行模式變更造成的額外直接成本;CD,ijk為活動i的第j個單元采用模式k的直接費用;xijk和xijk*為0-1變量,xijk=1為基準調度計劃中活動i的第j個單元采用模式k,xijk*=1為反應性調度計劃中活動i的第j個單元采用模式k*。

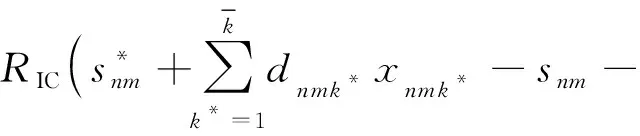
(4)

(5)

本文提出的優化模型的第二個目標函數是最小化反應性調度的快速修復范圍,即最小化反應性調度更改開始時間和執行模式的活動數量。可表示為

(6)

1.2 約束條件

由于調整只能針對尚未開始的單元,因此在調整時刻t正在進行和已經完成的單元采用基準調度計劃采用的執行模式。即

xijk*=xijk,ij∈Ft∪Pt

(7)

式(7)中:ij為活動i的第j個單元;Ft為調整時刻t已經完成單元的集合;Pt為調整時刻t正在進行的單元的集合。

同理,在調整時刻t正在進行和已經完成的單元的開始時間應該與基準調度計劃保持一致。即

(8)

頻繁改變執行模式和間斷活動會產生以下負面影響:①增加管理復雜性;②對項目質量產生負面影響(每次更改執行模式和間斷活動都會破壞已經建立的施工流程和質量控制措施,從而導致項目質量的降低);③會增加施工風險(每次更改都可能會導致不可預見的問題,例如材料供應或人員調整困難,這可能會給項目帶來不必要的風險);④增加施工人員的不滿,降低施工的效率。為了避免這些問題和簡化計算,假定一個活動最多間斷和改變執行模式一次,且間斷和改變執行模式的單元位置應保持一致。

為確保每個活動最多更改其執行模式一次,設置執行模式更改次數約束為

(9)

式(9)中:Ut為調整時刻t尚未開始的單元的集合。

為限定一個活動最多間斷一次,設置活動間斷次數約束為

(10)

為確保間斷和改變執行模式的單元位置保持一致,設置間斷和執行模式更改位置約束為

(11)

式(11)中:M為足夠大的正數。

為保證同一單元j,活動i的緊前活動h完成后,活動i才能開始,設置優先關系約束為

(12)

式(12)中:E為優先關系約束集合,(h,i)∈E表示活動h是活動i的緊前活動。

對于同一活動i,單元j+1只有在單元j完工后,單元j+1才能開始。設置邏輯關系約束為

(13)

2 基于強化學習的遺傳算法

鑒于上述優化模型是一個混合整數非線性模型,本文設計基于強化學習的遺傳算法對其進行求解。遺傳算法(genetic algorithm,GA)是一種元啟發式算法,模擬生物進化的自然選擇過程來求解優化問題,已廣泛應用于解決項目調度問題[5]。但是,GA的參數選取十分重要,將直接影響算法的求解效率。手動調整或隨機猜測GA參數十分耗時,且當求解問題發生變化時,需要重新調整GA參數。在本問題模型中,干擾事件影響的單元位置以及單元工期延誤的時間具有隨機性,很難找出一個通用的GA參數來使得GA在所有干擾事件發生情況下均保持良好的求解效率。因此,本文中通過Q-learning強化學習算法對GA進行改進,以解決這一問題。Q-learning是一種強化學習算法,通過做出最大化長期獎勵的決策來學習不同情景下的最優GA參數的選取,進而使GA在求解問題發生變化時也能繼續表現良好,將Q-learning算法與GA算法結合的算法更適合求解本文所提模型。

針對問題的雙目標屬性,本文采用ε約束算法獲得Pareto解[22]。ε約束算法的基本思想是將其中一個目標函數轉化為約束,并通過逐步放松約束建立一系列單目標優化問題進行求解。由于修復范圍的取值是離散的,因此本文將最小化修復范圍轉化為約束。

2.1 編碼方案

遺傳算法中最重要的一環是生成初始種群(隨機解的集合),它以名為染色體的字符串形式編碼,每個個體代表著一個解決方案。編碼方案如圖1所示,該圖顯示了一個只有4個活動的染色體。染色體的前四個基因表示采用的執行模式,后四個基因表示執行模式改變或活動間斷的位置。

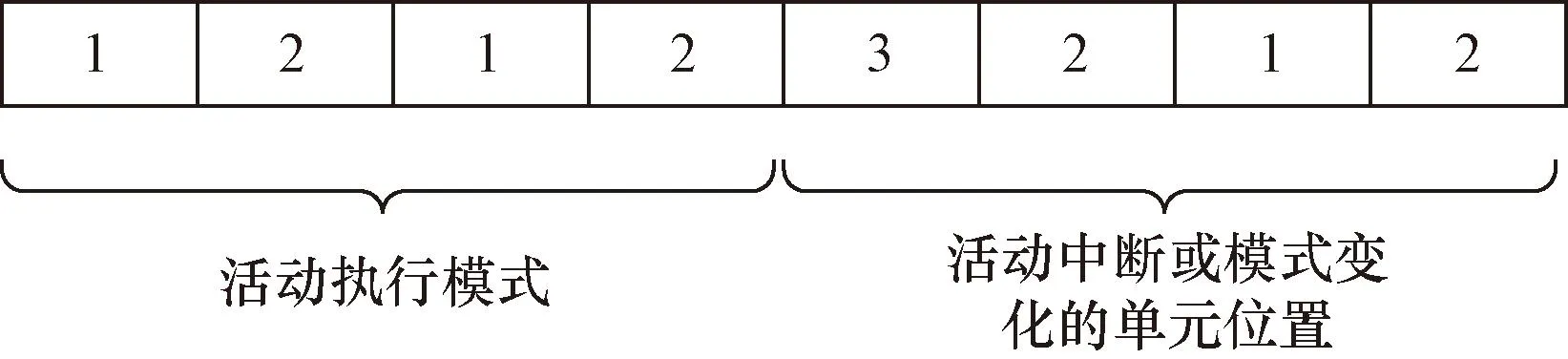
圖1 染色體編碼實例Fig.1 Chromosome coding example

2.2 算法流程

Step 1獲取項目的基本數據,例如基準調度計劃中活動各個單元的開始時間和執行模式,調整時刻,修復范圍等

Step 2初始化種群和Q-table。

Step 3計算適應度函數。

Step 4計算種群多樣性系數[23],確定種群狀態(State)。公式為

(14)

式(14)中:dt為種群多樣性系數,dt∈[0,1],dt越大,種群多樣性越好;t為迭代次數;mean(ft)為第t次迭代中種群適應度函數的平均值;max(ft)為第t次迭代中種群適應度函數的最大值;p為種群大小;Di為種群中與第i個個體適應度相同個體的數目。

種群分為4種狀態,dt∈[0,0.25]為狀態1,dt∈(0.25,0.5]為狀態2,dt∈(0.5,0.75]為狀態3,dt∈(0.75,1]為狀態4。

Step 5確定采取的動作。

根據種群狀態和Q-table采用ε-greedy策略確定采取的動作。具體來說,如果一個隨機數小于概率值ε∈[0,1],則隨機選擇一個動作,如果一個隨機數大于ε∈[0,1],則選擇Q-table中累計獎勵最大的動作。

本文將交叉和變異概率視為Q-learning算法中的動作。交叉概率通常取值在[0.5,0.999]之間,變異概率通常取值在[0.001,0.2]之間,本文在[0.5,0.999]和[0.001,0.2]內分別均勻取6個交叉概率和5個變異概率進行組合作為算法可以選取的動作。

Step 6選擇,交叉,變異操作。

選擇操作是模擬自然選擇中適者生存的過程。本文根據輪盤賭規則,基于個體適應度從當前種群中選擇后代。

選擇操作后,程序隨機選擇兩個個體作為父代,使用雙點交叉進行交叉操作。當隨機數大于交叉概率時,子代與父代相同,反之子代是由父代在隨機區間交換基因而產生的,如圖2所示。

圖2 交叉操作Fig.2 Crossover operation

變異操作則采用單點變異。只有在隨機數小于突變概率時,染色體才會發生突變,突變位置是隨機選擇的。如圖3所示。

圖3 變異操作Fig.3 Mutation operation

Step 7計算動作獎勵。

獎勵設置是更新Q-table的依據,也是Q-leaning算法的關鍵一環。

種群多樣性越高,找到最優解的可能性就越大。因此有必要對種群多樣性進行獎勵。計算公式為

(15)

算法迭代的目標是找到最優解。因此,如果在第t次迭代時種群的最優解[即max(ft)]得到了優化,應該獎勵這個動作,反之,如果最優解沒有得到優化,就應該懲罰這個動作。

(16)

如果第t次迭代時種群的平均適應度mean(ft)增加,說明整個種群已經得到了優化,應該給予獎勵。需要注意的是,如果平均適應度沒有變化,有非常大的概率是種群沒有改變,因此應該給予較大的懲罰。計算公式為

(17)

(18)

Step 8更新Q-table。

Q-table的更新方式為

(19)

式(19)中:Qt,State,Action為第t次迭代時Q-table在狀態和動作下的取值;α為衰減率;γ為學習率。

Step 9查看是否滿足終止條件。如果已經滿足終止條件,則算法終止,反之,則回到Step 3繼續計算。

算法的流程圖如圖4所示。

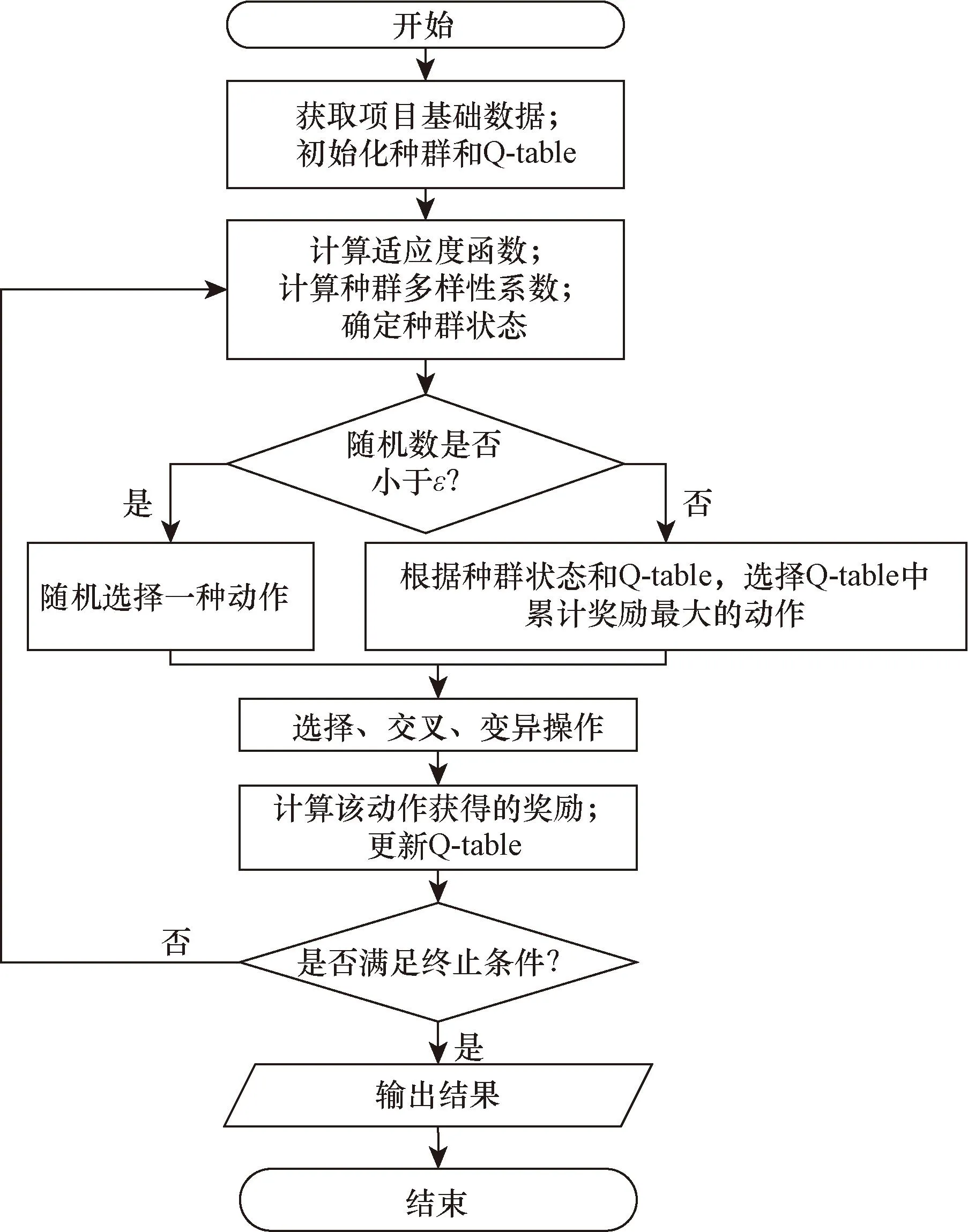
圖4 算法流程圖Fig.4 Workflow of the algorithm

3 案例分析

3.1 結果對比

選取丹錫高速公路一段長約5 km的建設項目為例以驗證本文反應性調度模型和算法的可行性。該重復性項目包括24 個活動,每個活動又分為5 個單元,每個單元長1 km。項目的截止日期是170 d,間接成本為每天31 600 元。表1列出了項目基礎數據。在不更改執行模式和間斷活動的情況下,以最小化建設總成本(包括直接成本和間接成本)為目標生成了基準調度計劃,如圖5所示。項目工期為170 d(滿足工期要求),總建設成本為70 008 800 元人民幣。在實際項目建設過程中,項目受到了干擾事件的影響。活動5的第2個單元的工期增加了2 d。

表1 項目基本數據Table 1 The basic data of the project

圖5 初始調度計劃RSM圖Fig.5 RSM diagram for baseline schedule

右移策略作為最簡單的項目反應性策略[8],是指不采取任何手段,將受到干擾事件影響的所有活動沿著時間軸向后推移的過程。本文分別使用右移策略和本文策略對該項目進行反應性調度,并進行結果對比分析。右移策略下的調度計劃如圖6所示,所有尚未開始施工的單元將延遲兩天開始,項目的工期增加至172 d,總建設成本增加至75 015 940 元人民幣,重新調度成本為5 007 140 元人民幣。

圖6 右移調度計劃RSM圖Fig.6 RSM diagram for right-shift schedule

本文模型得到的反應性調度成本-調整范圍的Pareto曲線如圖7所示,本文策略模型與右移策略模型的對比結果如表2所示。由結果可見,本文策略模型既能有效降低反應性調度成本,也能使項目迅速恢復至基準調度計劃。

表2 不同策略對比結果Table 2 Comparison of different strategies

圖7 帕累托曲線圖Fig.7 Pareto curves

由圖7可知,在一定修復范圍內,本文策略得到的反應性調度成本隨著修復范圍的增加呈現下降趨勢。可以解釋如下:隨著修復范圍的增加,更多活動可以參與反應性調度,可以通過增加額外直接成本(或偏差成本)來使偏差成本(或額外直接成本)更大幅度降低,從而使反應性調度成本減少。

由表2可知,采用本文策略得到的反應性調度計劃成本、工期和受影響的活動數目均不劣于右移策略得到的反應性調度計劃。這很容易理解,本文策略可以更改活動的執行模式和允許間斷,具備了更多應對干擾事件的手段,因此反應性調度成本和受影響的活動數目較小;其次,在一定修復范圍內,項目恢復至基準調度計劃的時間隨著修復范圍的增加呈現上升趨勢。這是因為隨著修復范圍的增加,受影響的活動數目增加,導致恢復至基準調度計劃的時間增加;最后,當修復范圍增加至某一數值時,最小的反應性調度成本不再發生變化。這是因為調整活動的范圍越廣,偏離基準調度計劃的活動就越多,將導致極高的偏差成本,此時其他成本的降低已無法彌補偏差成本的增加。

值得注意的是,表2中還存在以下兩種現象。

(1)相比修復范圍為1 個活動,修復范圍為2 個活動時的反應性調度計劃恢復至基準調度計劃的時間更早。原因如下:修復范圍約束為1 個活動時,反應性調度計劃僅允許調整延誤活動(活動5),由于其緊前活動(活動4)不受干擾,恢復至基準調度計劃(活動5的完工時間)是第47 天;修復范圍為2 個活動時,通過更改緊前活動(活動4)的執行模式,使活動4提前完工,進而導致受影響的最后一個活動可以更早的完成,因此可以較早的恢復至基準調度計劃。

(2)當修復范圍約束大于等于4 個活動時,額外直接成本為-507 224 元,這是因為活動5、活動7和活動8通過變更執行模式和允許間斷等手段使得活動6部分單元可以采用直接成本更小但工期更長的執行模式,導致額外直接成本費用小于0。

為了驗證所設計算法的有效性,將遺傳算法(GA)應用于本算例進行測試對比。參數設置如下:種群大小設置為40,交叉和變異概率設置為0.8和0.1,學習率和衰減率設置為0.9和0.2,概率值ε設置為0.7,運行時間為10 s,取10次可行解。算法對比結果如表3所示。

表3 算法性能對比Table 3 Comparison of algorithm performance

根據對比結果可知,本文相同迭代時間下的平均調度成本,平均偏差,最大偏差均比遺傳算法的求解結果好,這是因為Q-learning算法優化了遺傳算法的參數選取,從而使算法收斂性能提高,說明了本文所設計的算法性能有效性。

3.2 蒙特卡洛模擬

為了進一步說明本文模型和算法的有效性和穩健性,采用蒙特卡洛模擬5 000 次干擾事件的發生。干擾事件的發生位置隨機選擇,單元工期的延誤時間為1～3 d,修復范圍約束為1～4 個活動。

對不同干擾事件下本文策略求得的最優反應性調度計劃進行分析可知,本文策略得到的最優調度計劃的工期仍不劣于右移策略;隨著修復范圍約束增加,本文策略仍存在反應性調度成本呈現下降趨勢,恢復至基準調度計劃的時間呈現上升趨勢的特點。因此本文模型具有很好的有效性和穩健性。

算法運行時間設置為10 s,進行蒙特卡羅模擬5 000 次的算法對比結果如表4所示。

本文算法和遺傳算法求解出可行解比例較低的原因主要是部分情況下修復范圍過小,導致項目不存在滿足修復范圍約束的可行解。例如,活動16的第1個單元延誤1 d,不存在修復范圍為一個活動時的反應性調度計劃。

由表4可知,本文算法在可行解中非支配解比例以及求得可行解比例均高于遺傳算法,本文算法求得調度計劃的調度成本比遺傳算法求得調度計劃的調度成本低,本文算法求解性能更好。

4 結論

本文研究了基于快速修復策略的重復性項目反應性調度問題。作者首先對研究的問題進行了界定,研究的目標分別為最小化反應性調度成本和最小化修復范圍。在此基礎上構建了反應性調度模型,針對該模型設計了一種Q-learning算法與遺傳算法相結合的算法,并與單獨的遺傳算法進行對比。最后通過高速公路的案例驗證本文所提模型和算法的有效性,并得出如下結論。

(1)通過反應性調度可以顯著降低由干擾事件引起的調度成本,通常調度成本隨著修復范圍的增加而降低。

(2)當修復范圍超過某個臨界值時,增加修復范圍并不會降低調度成本。

(3)Q-learning算法與遺傳算法相結合的算法在求解該類問題上比遺傳算法具有更好的求解效率。

本文可為項目管理者進行反應性調度時提供決策依據。