基于自適應響應面法的白車身結構輕量化設計
侯俊劍, 王泳, 鐘玉東, 趙登峰, 何文斌, 周放
(鄭州輕工業大學機電工程學院, 鄭州 450000)
白車身是汽車部件的一個重要組成部分,白車身結構占整車質量的40%。目前許多汽車制造行業已經把車身的輕量化的設計作為重點研究方向,并且美國研究機構通過實驗發現汽車質量每減少10%,能夠節省7%的燃油消耗量,如果每減輕1 kg的汽車總重量能夠節省3~4美元的制造成本[1]。因此如何有效地進行白車身輕量化設計,是目前汽車行業最關心的問題之一。Kiani等[2]通過分析白車身模型的靜剛度和動剛度,然后利用多目標優化進行質量最小化求解,該方法不僅降低了質量,還提高了車身結構剛度。王權[3]針對某轎車的白車身結構為基礎進行輕量化設計,采用靈敏度的分析方法和局部的輕量化的結構尺寸設計及形狀輕量化設計方法對白車身結構進行輕量化設計使白車身減重25.123 kg。蔡珂芳[4]以“合適的材料用在合適的部位”為設計理念,基于高強鋼、鋁合金和碳纖維復合材料等輕質材料設計了混合材料白車身,并通過優化方法對碳纖維復合材料地板、梁結構截面尺寸、材料屬性以及一些關鍵設計變量進行多目標優化設計,實現了結構-材料-工藝一體化設計,建立了白車身開發設計流程。李長玉等[5]通過白車身的固有頻率以及剛度值為依據,采用單目標尺寸優化的方法對白車身的重量進行減重優化,并且將優化后的結果和優化前進行對比。結果表明:通過優化白車身減重23.1 kg,減重比例達5.31%。吳鵬興等[6]以商用車駕駛室為研究對象,進行輕量化設計。通過靈敏度分析篩選設計變量,并利用第二代非支配排序遺傳算法求最優解。針對某白車身進行輕量化研究,使得在白車身的質量下降的同時保障本身的模態頻率、剛度和強度性能。當白車身的質量下降的同時又能達到節能減排的效果。利用實驗采樣方法、響應面的替代模型和優化求解方法能夠形成系統性的結構優化設計方法。目前在白車身輕量化的研究中系統性的結構優化設計比較少,在以往的優化設計當中主要是零件的拓撲優化,面對大量的零件進行的拓撲優化極為復雜。通過自適應響應面方法解決大量零件個數的優化設計,在縮短產品優化設計周期的同時來促進汽車行業的發展。
1 自適應響應面方法
1.1 響應面法
在進行實驗設計與分析時,變量跟響應之間的關系是未知關系,如果假設能用未知系數表達變量跟響應之間的關系,就形成數學表達式,因此將這種形式的方法稱為響應面法[7]。通常情況下建立的響應面為二次多項式,如式(1)所示。
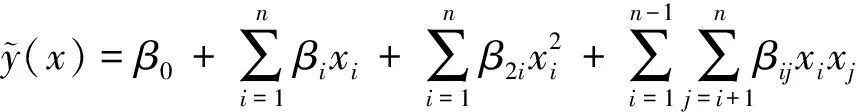
(1)
式(1)中多項式系數可以用最小二乘法來確定,通過創建的響應面需要進行擬合,利用相對均方根誤差、平均相對誤差和最大相對誤差評定模型的精度,最后得出擬合精確度[決定系數,如式(2)所示],擬合精確度越接近1代表響應面模型越精確。
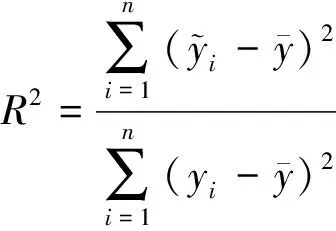
(2)
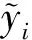
1.2 自適應響應面法
如果利用數值方法對創建的響應面進行迭代尋優時,響應面的精度較差和設計空間較大都會導致尋求最優解發生困難。自適應響應面法(adaptive response surface method,ARSM)[8]是一種響應面模型跟實驗設計相結合的方法,它通過每一步迭代之后把響應值跟約束值相比較,把大于約束值的設計變量范圍進行丟棄,滿足的話進行下次迭代,不斷縮小設計變量范圍,最終求得全局最優解。自適應響應面利用式(3)進行目標函數與約束函數的擬合。

(3)
利用自適應響應面法進行迭代將在原有得設計變量區間內更新變量值,不斷調整自適應函數,因此響應面將會不斷地更新,擬合精度也在不斷地提升,使得優化結果不斷逼近真實值。利用此方法進行優化求解時,需要定義變量和優化目標和約束條件:①設計變量,定義需要優化的變量和范圍;②約束條件,定義需要約束的頻率、應力與位移等;③優化目標,定義需要得到目標值最小或最大。
2 白車身結構模型的建立及處理
2.1 構造三維有限元模型
通過三維繪圖軟件繪制白車身模型(圖1),共創建411個零部件,這些零件的組合形成了發動機機艙,左右側圍板金總成、車頂蓋總成、后車箱、前圍鈑金件總成等,此白車身還包含前后擋風玻璃。

圖1 白車身三維模型
2.2 白車身結構網格劃分及單元連接
通過把三維白車身模型導入有限元分析軟件,進行模型簡化,忽略一些微小的工藝特征為了為后面縮減計算工作量做準備,同時需要對一些復雜但不影響計算準確性的地方做簡化處理。在對模型做簡化處理之后,通過白車身的三維模型來生成有限元網格。在劃分二維網格之前,需要把一些鈑金部件抽取網格中面,使其生成二維平面,在二維平面上劃分網格(圖2)。二維網格中有三角形網格和四邊形網格,但是三角形網格的計算量會增多且網格均勻性和精細度難以保證,因此應減少三角形網格的出現。在對一些螺栓孔的網格劃分時需要一圈網格單元來模擬墊片,以汽車后地板為例,此處需要對一些圓孔劃分washer(圖3)。劃分白車有限元網格需要做一些質量檢查(表1),針對不滿足網格質量應做出修改。

表1 有限元網格質量要求

圖2 白車身側圍的有限元網格

圖3 圓孔構建washer
2.2.1 零部件之間的連接
在有限元網格中需要對劃分好的網格進行連接關系的創建,比如說焊接和粘接。對于一些受載荷力的地方需要用到剛性連接,使載荷平均分散到各個部位。
2.2.2 材料屬性的設置
在對各零部件劃分網格之后,應設置其材料屬性,進行材料和零部件的關聯。本課的白車身大部分采用的是鋼材,前機艙的支架采用高強度鋼,前后擋風玻璃采用玻璃材質(表2)。通過材料屬性的設置才能分析出白車身各部件的力學特性。

表2 白車身部件的材料屬性
建立的白車身有限元模型如圖4所示,然后就能依據有限元模型進行模態和剛度分析。

圖4 白車身有限元模型
3 白車身結構模態、強度和剛度分析
利用白車身的有限元模型進行模態和靜剛度分析,針對其分析結果來進行優化對比,因為本模型的白車身中包含了前后擋風玻璃,因此模態和靜剛度略大。
3.1 模態分析
白車身的模態分析[9]是研究白車身結構的本身特有屬性,通過模態分析可以看出白車身的固有頻率和振型等信息。在模態分析中是自由狀態,不需要添加約束。通過模態分析能夠得出白車身的前六階模態分別為40.63(圖5)、44.13(圖6)、45.95、47.92、53.61、54.42 Hz。

圖5 一階模態振型云圖(40.63 Hz,一階扭轉模態)

圖6 二階模態振型云圖(44.13 Hz,一階彎曲模態)
3.2 靜剛度分析
本課題的白車身是一種承載式車身,來自路面和乘客等多種載荷將由車身來承受。剛度分析就是研究結構抵抗變形的能力,只有剛度性能好,車身的整體框架才不會大面積變形。
3.2.1 剛度分析工況設置
在對白車身進行彎曲剛度分析[10]時,需要約束白車身的前后左右共計4個懸架的自由度,在座椅附近的左右兩邊施加相同的1 000 N的Z軸垂直線下方向的載荷(圖7)。在對白車身進行扭轉剛度分析[11]時,需要約束白車身的后面兩個懸架的自由度,在前懸架的左右兩邊同時施加Z軸相反的1 000 N載荷(圖8)。
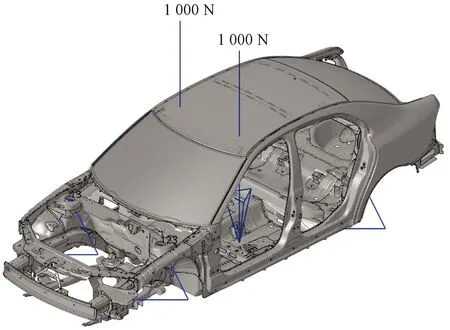
圖7 彎曲剛度的工況設置

圖8 扭轉剛度的工況設置
3.2.2 剛度分析結果
在進行彎曲剛度的工況設置之后進行計算,得到最大Z向負位移為0.404 mm(圖9)。在進行扭轉剛度的工況設置之后進行計算,得到最大Z向正位移為0.63 mm(圖10)。
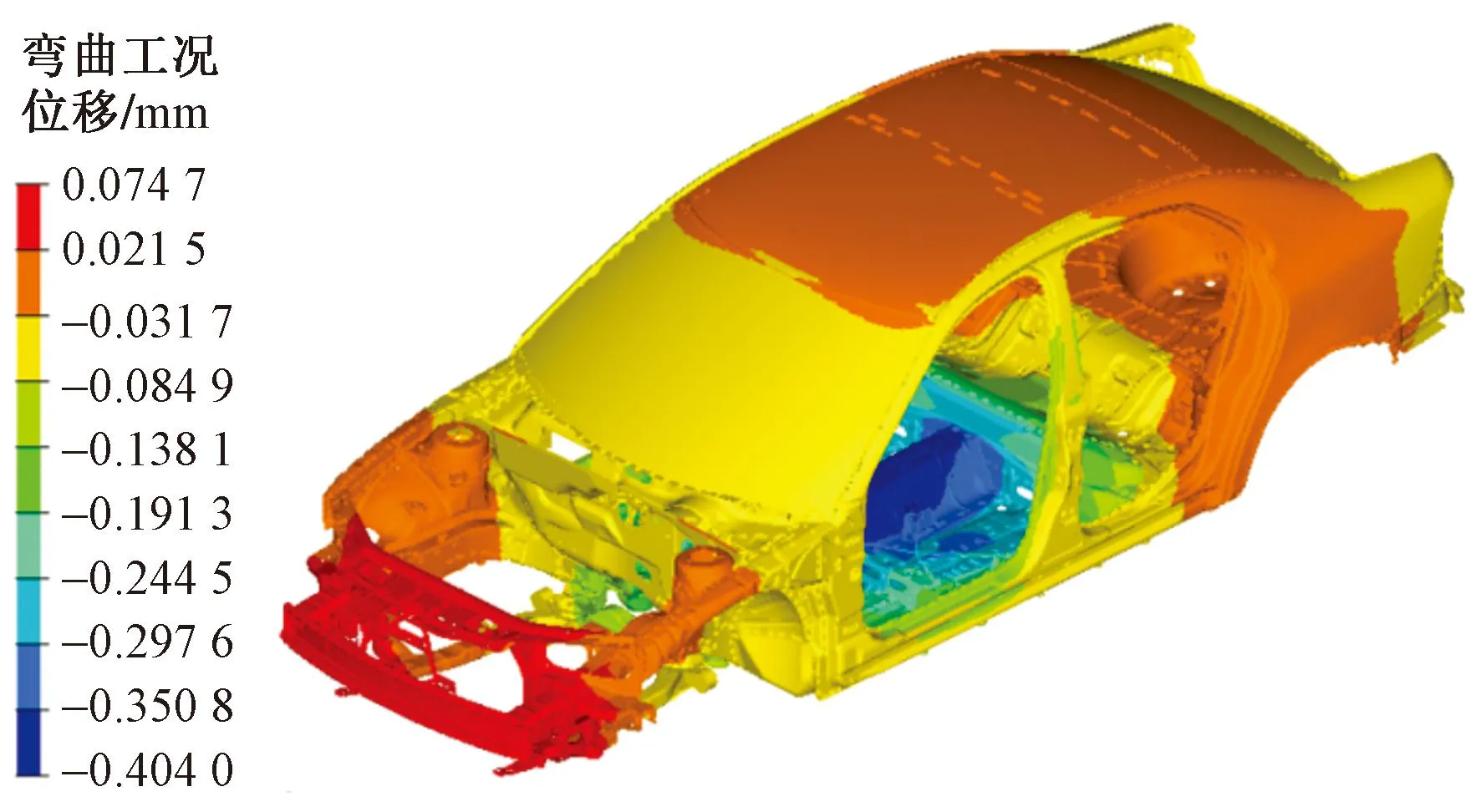
圖9 彎曲工況的Z向位移云圖
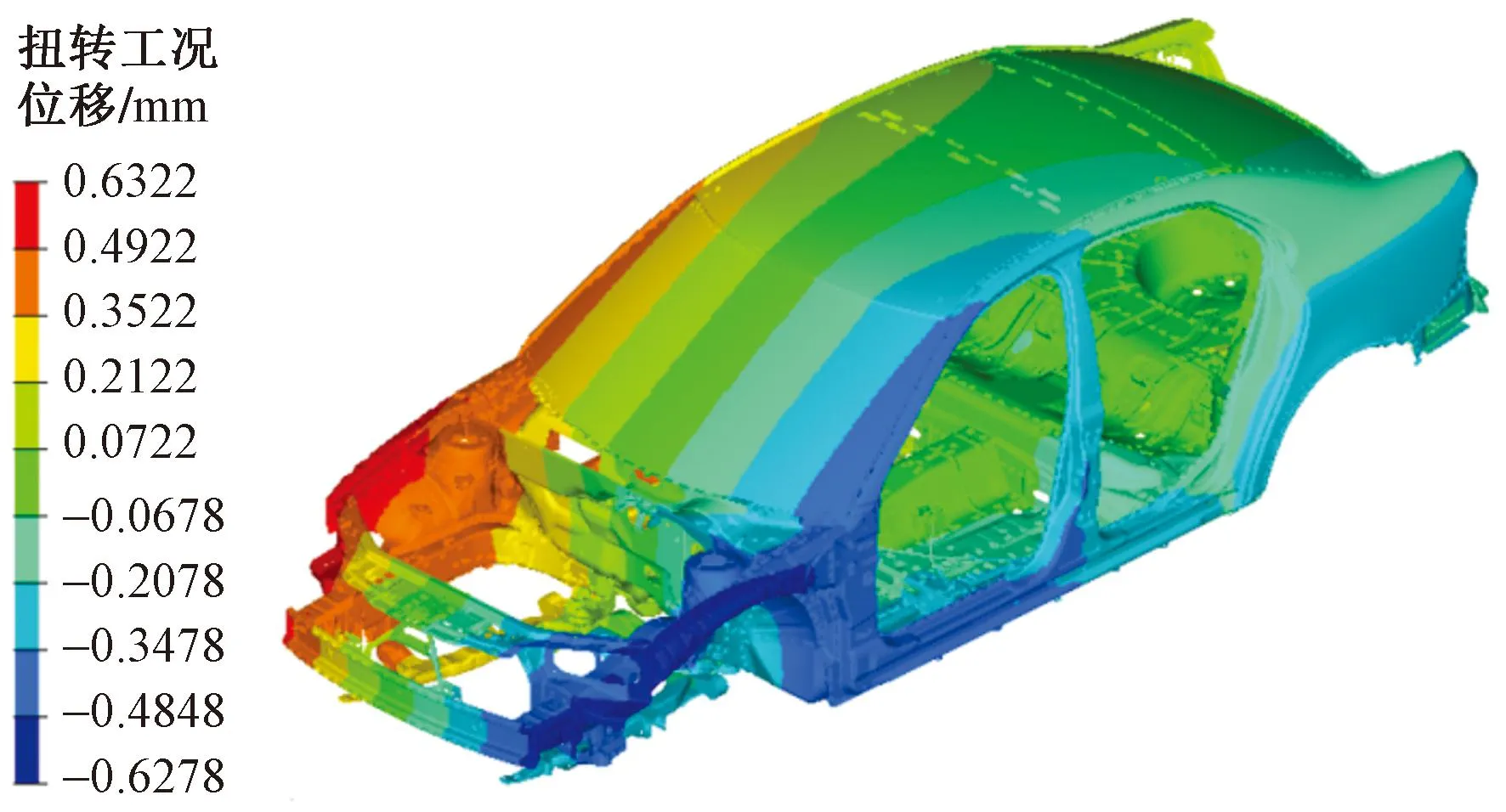
圖10 扭轉工況的Z向位移云圖
最后得出的彎曲剛度為18 761.72 N/mm。相對而言一般的帶擋風玻璃的白車身的彎曲剛度大于12 000 N/mm,因此此白車身的彎曲剛度滿足需求。白車身的扭轉剛度為20 279.41 N·m/rad。相比較其他車型,大半部分的燃油車的扭轉剛度大于15 000 N·m/rad,因此滿足設計要求。
3.3 白車身的靜強度分析
3.3.1 靜強度分析工況設置
本課題白車身的強度分析[12]主要針對垂直沖擊、轉彎和制動3個工況如表3所示。在載荷中,給白車身模型以加速度的方式施加作用力模擬3種工況,X、Y和Z為施加加速度的方向,g為重力加速度,取9 800 mm/s2。

表3 3種工況的設置
3.3.2 白車身靜強度分析結果
在垂直沖擊工況的分析當中(圖11),最大應力為175.98 MPa,最大應力的板件(鈑金件編號:680340,圖12)的材料是B340LA鋼,它的屈服極限為38 0 MPa,滿足要求。

圖11 垂直沖擊工況應力云圖
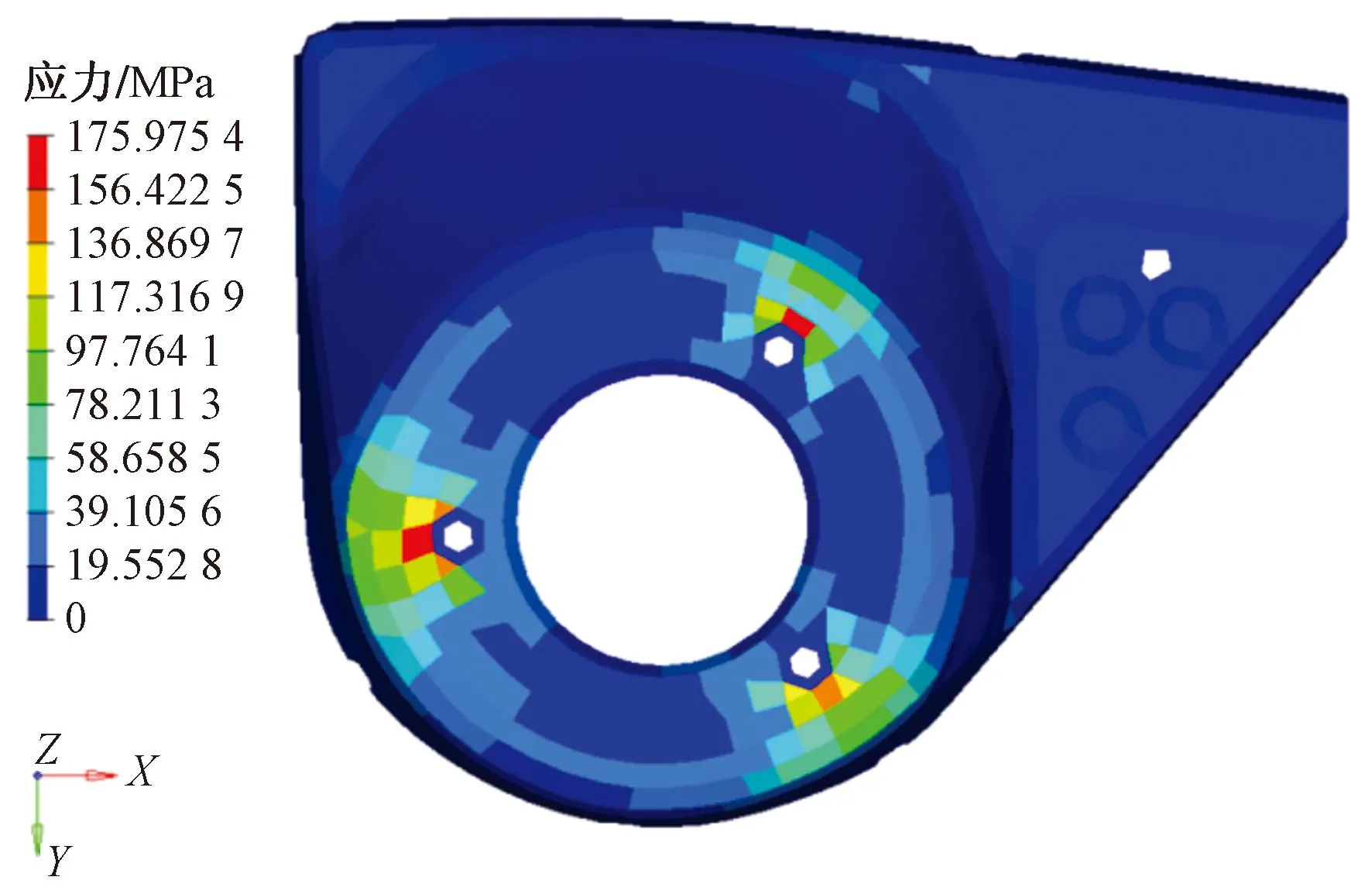
圖12 垂直沖擊工況最大應力板件云圖
在制動工況的分析當中(圖13),最大應力為192.1 MPa,最大應力的板件(鈑金件編號:683220,圖14)的材料是B340LA鋼,它的屈服極限為380 MPa,滿足要求。

圖13 制動工況應力云圖

圖14 制動工況最大應力板件云圖
在轉彎工況的分析當中(圖15),最大應力為73.01 MPa,最大應力的板件(鈑金件編號:683340,圖16)的材料是B340LA鋼,它的屈服極限為380 MPa,滿足要求。

圖15 轉彎工況應力云圖
4 白車身結構的尺寸優化設計
4.1 靈敏度分析
靈敏度分析[13]從數學的角度來講,相當于有一個可導函數F(xi),則它的一階靈敏度就是函數對自變量的微分[式(4)]。

(4)
式(4)中:SenF(x)為一階靈敏度;F(xi)為可導函數;xi為自變量。
靈敏度的正負表示變量與響應之間的正負相關性,靈敏度絕對數值的大小表示板件厚度對每個工況影響的劇烈程度。通過對白車身的模態和剛度靈敏度分析可以看出各鈑金件對相應工況的影響,此時還需要進行相對靈敏度計算[式(5)]。使它們都在單位質量靈敏度的情況下進行鈑金件篩選(表4),此時能更有效地排除質量因素去分辨各鈑金件對模態和剛度的影響。
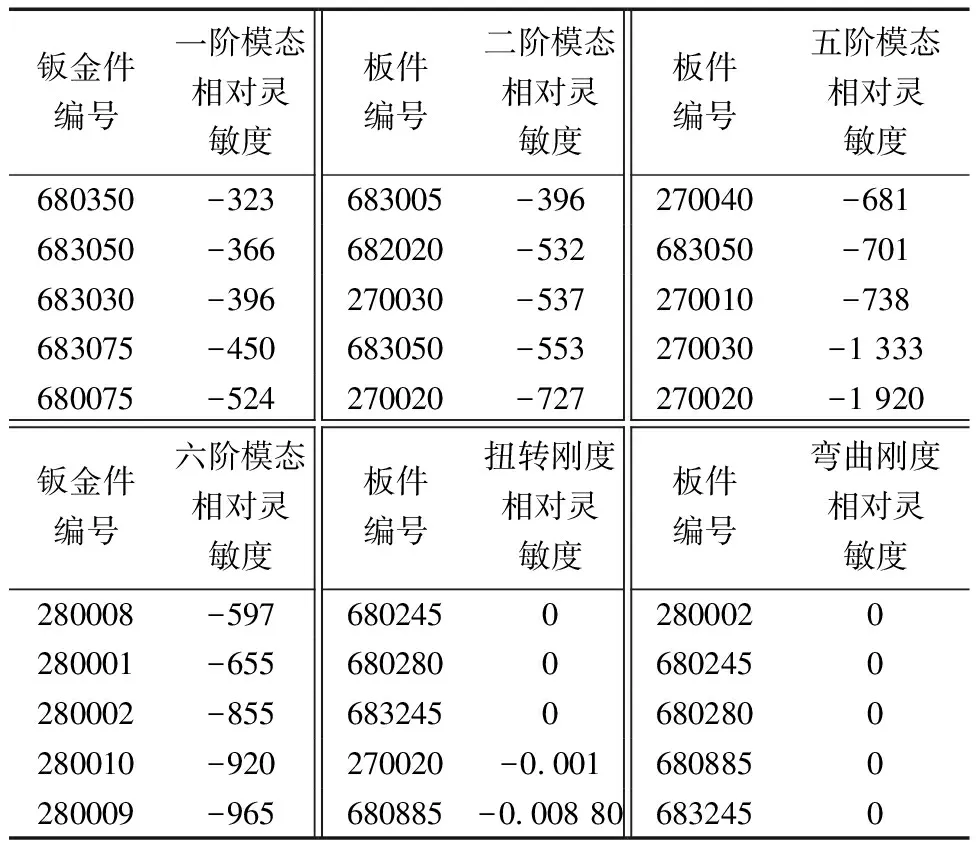
表4 8個工況中相對靈敏度值較小的鈑金件

(5)
式(5)中:RSm為模態相對靈敏度;Sm為模態靈敏度;Sq為質量靈敏度;RSk為剛度相對靈敏度;Sk為剛度靈敏度。
此時的篩選出來的設計變量還是太多,為了選擇更加有效的設計變量,對每個工況相對靈敏度最小的30個鈑金件進行再次挑選。通過把其中質量大于1 kg的挑選出來作為設計變量,最后挑選出來15個設計變量,如圖17和表5所示。

表5 作為設計變量的15個鈑金件

圖17 作為設計變量的鈑金件
4.2 田口實驗方法
在進行設計變量的組合時有全因子實驗、部分因子實驗和田口實驗等。Taguchi實驗[14]使得樣本點分布均勻,并且相比全因子和部分因子試驗次數更少。在建立田口實驗時,利用篩選出的15個變量作為因子,把鈑金件厚度浮動范圍50%上下劃分成三水平,質量、頻率、剛度位移和強度應力響應。通過對54次不同鈑金件厚度的組合進行計算(表6)。

表6 田口實驗設計
通過田口實驗設計的實驗表進行了54次實驗,得到的質量變動情況如圖18所示。一階模態頻率變動情況如圖19所示。

圖18 田口實驗中質量變動情況
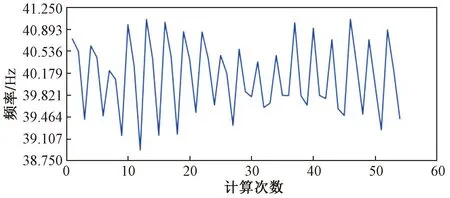
圖19 田口實驗中一階模態頻率變動情況
4.3 響應面創建
利用田口實驗方法進行的54次實驗進行響應面的創建,通過響應面構建出的變量和響應之間的關系來替代本身模型長時間的計算。在進行響應面創建時需要進行擬合(表7),用到的方法有最小二乘回歸(least squares regression,LSR)法,和移動最小二乘法(moving least squares modal,MLSM)[15]。
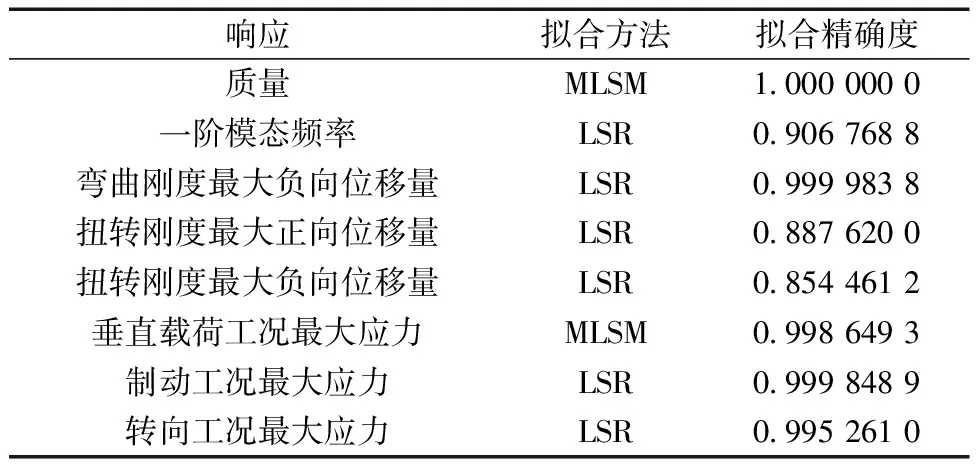
表7 響應面的擬合
最終得到響應面的模型,分別有質量的響應面(圖20)、一階模態頻率的響應面(圖21)、最剛度工況最大位移的響應面(圖22)和強度工況最大應力的響應面(圖23)。

圖20 質量響應面

圖21 一階模態頻率響應面

圖22 彎曲工況Z向最大負位移響應面

圖23 制動工況最大應力響應面
4.4 模型最優化求解
基于創建出來的響應面模型利用自適應響應面方法進行模型最優化求解。首先定義模型的15個設計變量,然后把一階模態頻率,剛度分析中最大Z向位移和強度分析中最大應力設為約束條件,最后把質量最小設為目標。通過21次迭代計算得到了最優結果,此時質量最小且滿足其他約束條件。
通過ARSM求解出來的鈑金件厚度有的存在幾位小數,這種情況并不利于生產制造和加工,因此保留3位小數(表8)。
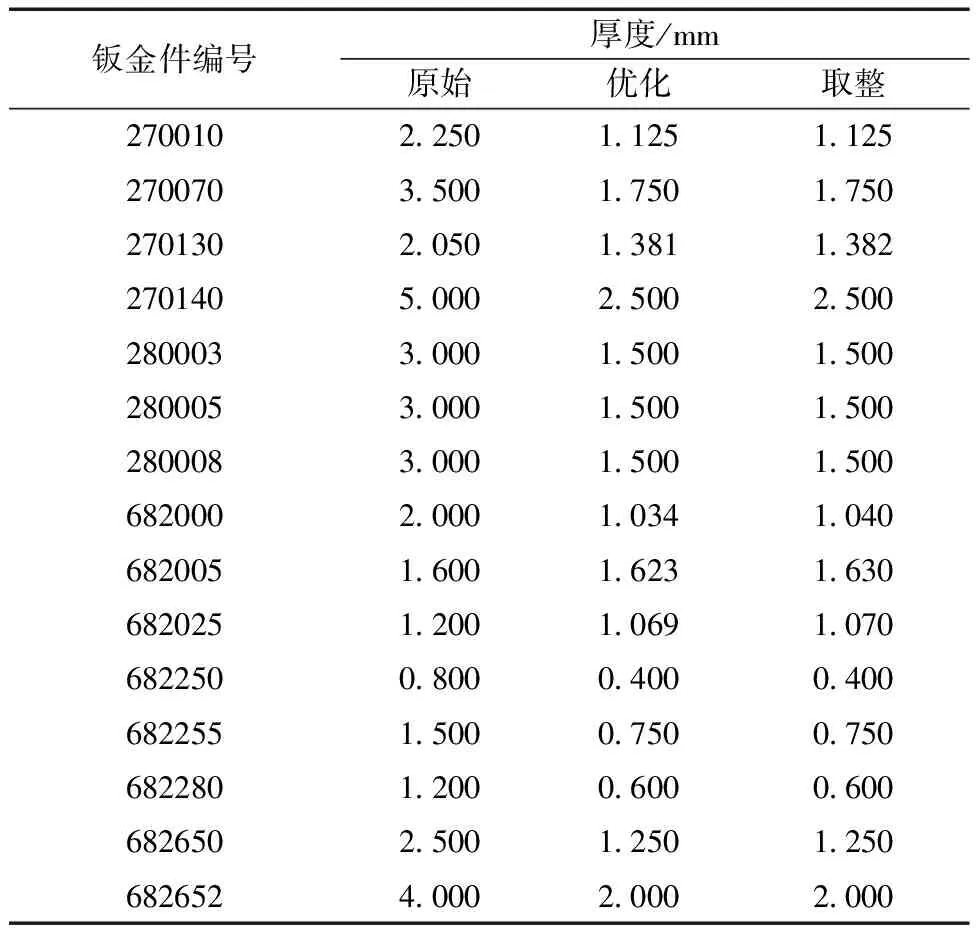
表8 各鈑金件厚度調整
在鈑金件厚度的基礎上,針對響應結果進行對比(表9),可知質量減輕了18.924 kg,一階模態頻率提升了約0.616 44 Hz,達到41.254 Hz(圖24)。優化后進行仿真實驗,剛度分析中最大Z向位移有輕微增大(圖25和圖26)。經過計算優化后的彎曲剛度為18 744.14 N/mm,比原本的彎曲剛度18 761.72 N/mm降低了17.58 N/mm,但是仍然滿足大于12 000 N/mm的要求。優化后的仿真扭轉剛度為20 219.28 N·m/rad,比原本的扭轉剛度20 279.41 N·m/rad降低了60.13 N·m/rad,但是仍然滿足大于15 000 N·m/rad的要求。強度工況的最大應力結果有顯著下降,如圖27~圖29所示,低于材料屈服極限滿足要求。
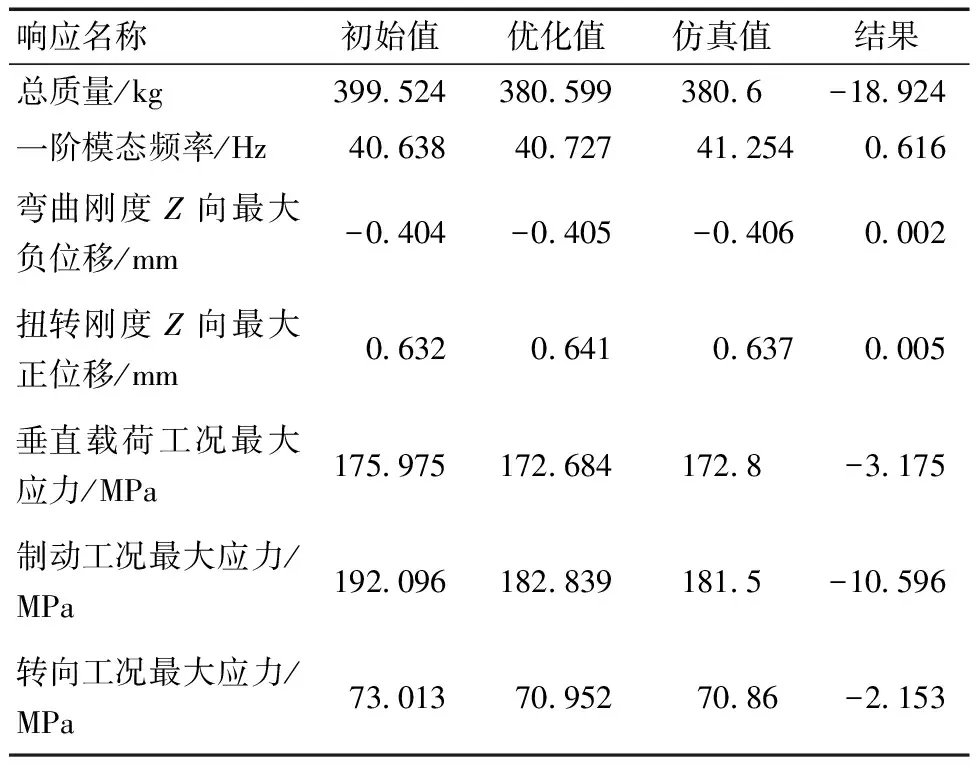
表9 優化后結果對比
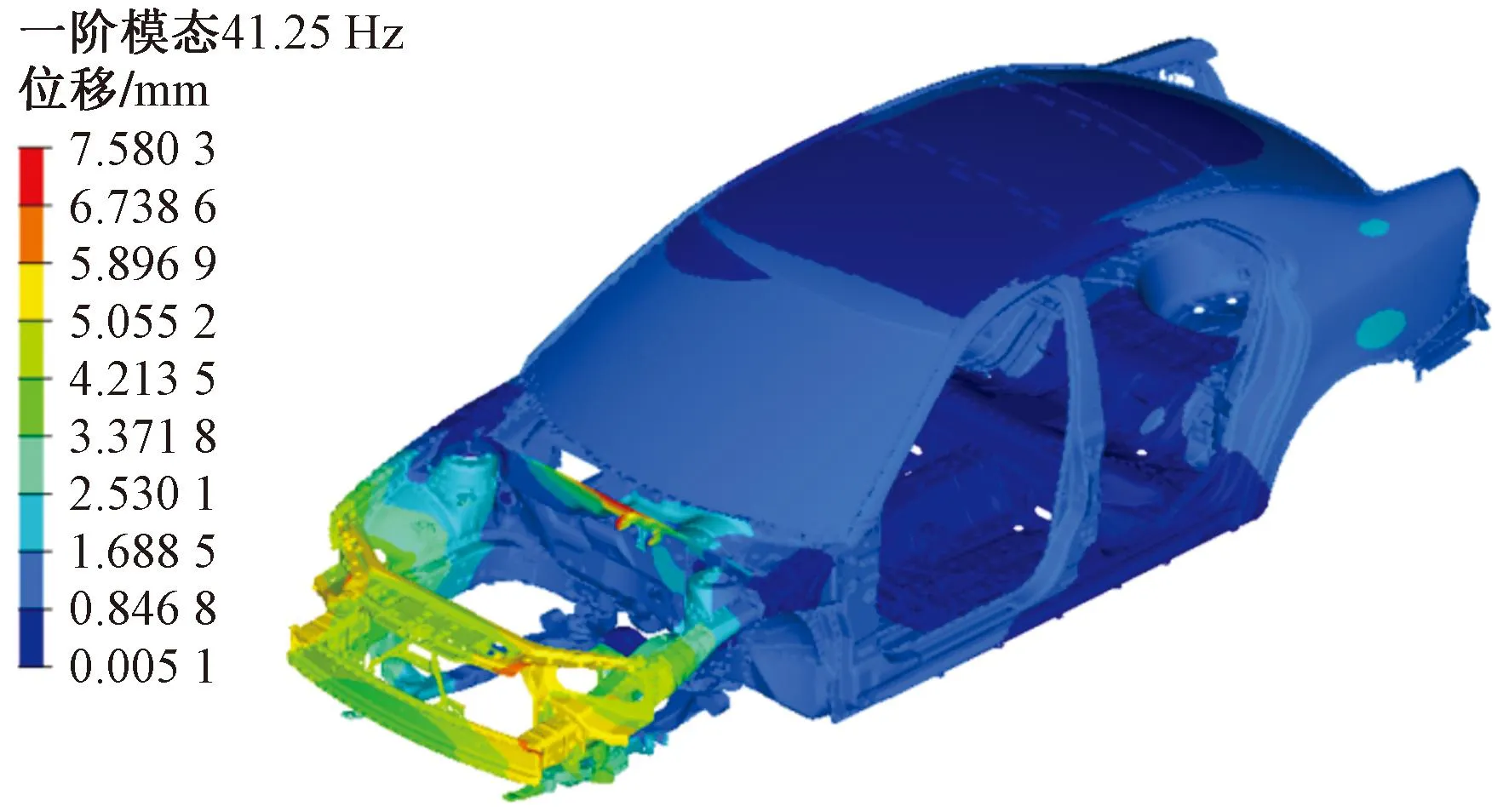
圖24 優化后的一階模態云圖
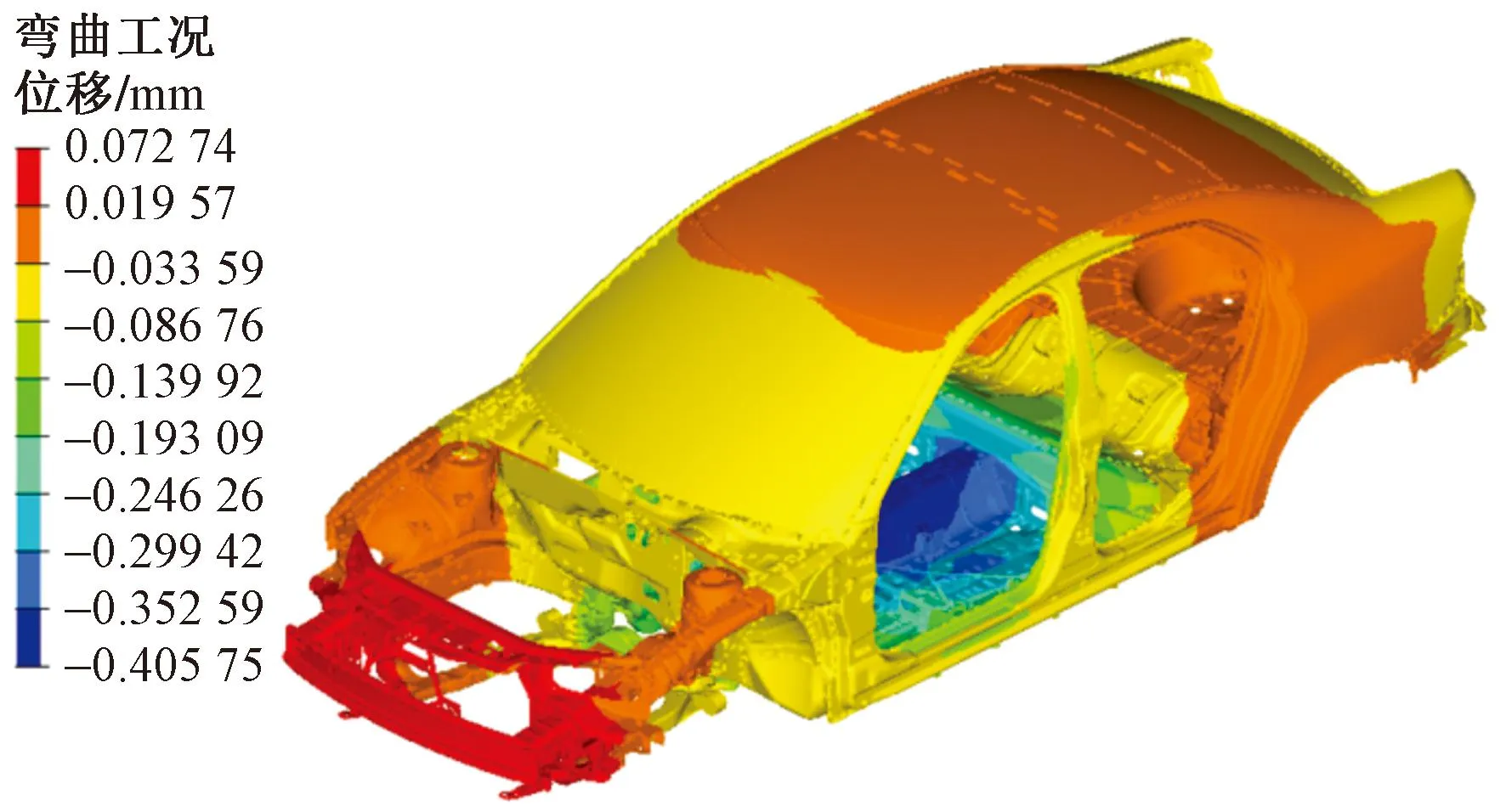
圖25 優化后的彎曲剛度Z向位移云圖
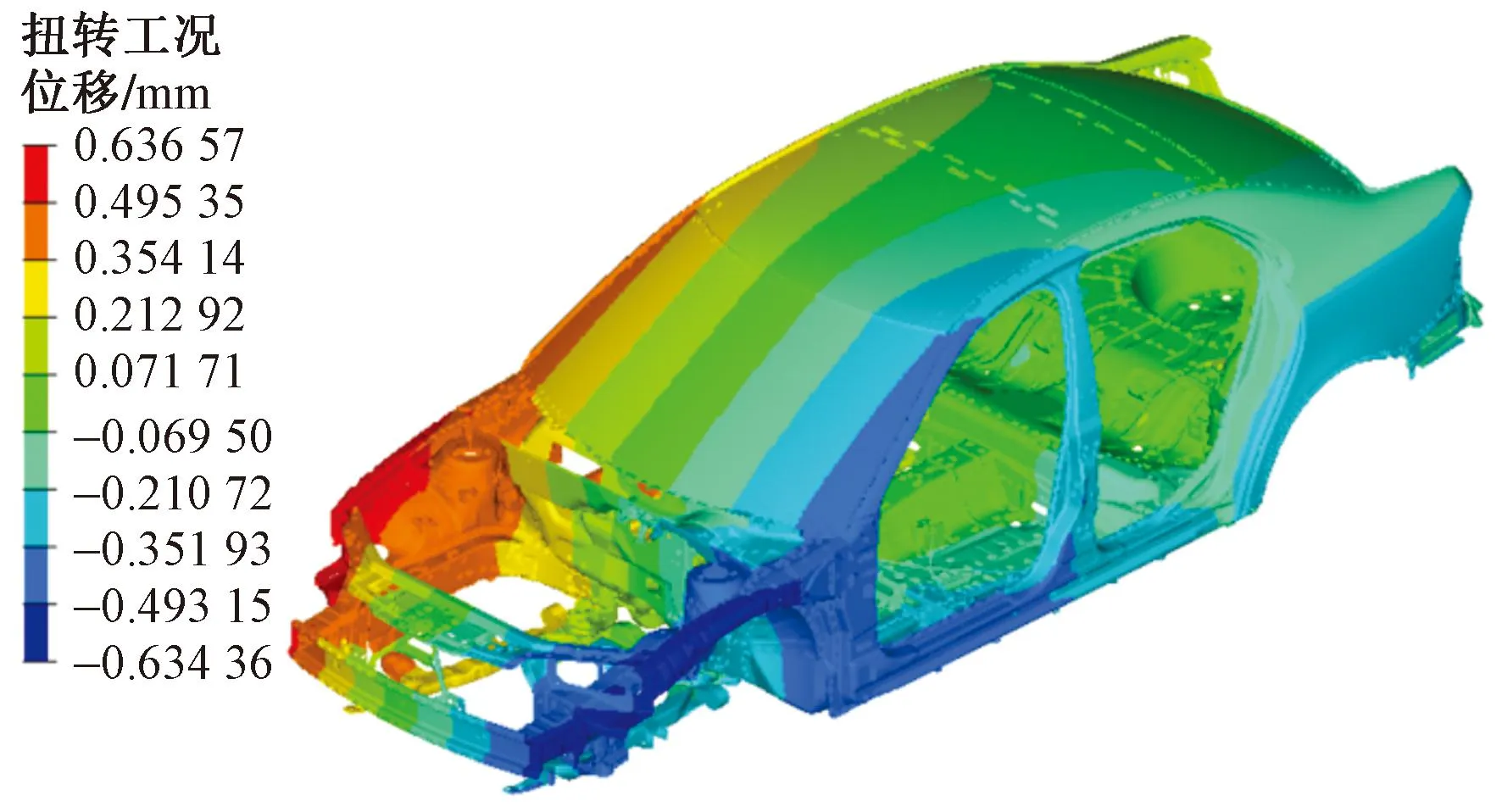
圖26 優化后的扭轉剛度Z向位移云圖

圖27 優化后的垂直載荷工況應力云圖

圖28 優化后的制動工況應力云圖

圖29 優化后的轉向工況應力云圖
5 結論
基于某白車身模型進行輕量化設計,分析白車身的模態、剛度和強度。通過利用靈敏度分析篩選15個鈑金作為變量,利用田口實驗進行15因子3水平實驗設計,基于響應面方法對模型進行優化求解,并進行仿真實驗對比得出以下結論。
(1)利用自適應響應面法求最優解使白車身減重18.924 kg,占整體質量的4.736 9%。
(2)通過對白車身進行輕量化優化設計,使得白車身的一階模態頻率從40.637 56 Hz上升到41.254 Hz。從而證明對結構的模態相對靈敏度為負的鈑金件減輕確實能提升白車身的模態頻率。
(3)雖然白車身的彎曲剛度優化后為18 744.14 N/mm,降低了17.58 N/mm,但是仍然滿足大于12 000 N/mm的要求。優化后的扭轉剛度為20 219.28 N·m/(°),比原本降低了60.13 N·m/(°),但是仍然滿足大于15 000 N·m/(°)的要求。
(4)通過此方法進行的輕量化設計使得白車身的3個靜強度工況的最大應力均有所下降。

