基于ISSA-SVM的鉆井卡鉆事故預測

陳曉, 張奇志*, 王鑫, 黃圣杰, 陳浩宇

(1.西安石油大學電子工程學院, 西安 710065; 2.陜西省油氣井重點測控實驗室, 西安 710065;3.西安石油大學新能源學院, 西安 710065)

在鉆井作業(yè)過程中,由于地層復雜或司鉆操作失誤的影響,卡鉆事故時有發(fā)生,導致對現(xiàn)場施工人員的人身安全造成極大的威脅。若不及時發(fā)現(xiàn)并采取措施,將導致危險情況延續(xù),造成無法挽救的后果,如導致井眼報廢等[1]。因此,對突發(fā)的卡鉆事故及時的分析與預測,進而采取有效的預防措施,是對井眼與施工人員人身安全強有力的保護。但由于技術(shù)局限性,工作人員僅能通過傳感器采集到的實時數(shù)據(jù)進行粗略的人為判斷,人為主觀因素使得判斷的準確性差。

中外學者提出了許多方法來預測卡鉆事故。蘇曉眉等[2]為預測復雜鉆井工況下的沉砂卡鉆,使用K均值(K-means)聚類方式對數(shù)據(jù)進行訓練以預測卡鉆事故,但該方法需多次運行才能得到最優(yōu)解。劉建明等[3]提出了基于主成分分析法(principal component analysis, PCA)與隨機森林(random forest, RF)相結(jié)合的方法以預測卡鉆事故,得出兩者結(jié)合可提高模型的運算效率。富浩等[4]提出了一種基于PCA-SVM的預測方法,預測準確率高,但模型僅適用于井眼不清潔導致的卡鉆事故預測,其他預測仍需要進一步研究。Nakagawa等[5]采用一種無監(jiān)督的學習方法來預測卡鉆事故,并將其應用于卡鉆事件,發(fā)現(xiàn)在某些情況下,觀察值和預測值之間的誤差在卡鉆之前就增加了,以此實現(xiàn)卡鉆的預測將導致預測的準確性降低。Brankovic等[6]使用機器學習的方式建立了統(tǒng)計模型,將提取出的泥漿錄井數(shù)據(jù)與歷史卡鉆事故結(jié)合,并根據(jù)建立的統(tǒng)計模型和實時數(shù)據(jù),繪制動態(tài)卡鉆預測的風險地圖,驗證該卡鉆預測風險地圖能夠及時預測卡鉆事故。

PCA是一種提取數(shù)據(jù)特征的方法,其在保留原有數(shù)據(jù)信息的基礎(chǔ)上,通過降低數(shù)據(jù)維度來提高運算效率。支持向量機(support vector machines, SVM)在解決小樣本和非線性問題中表現(xiàn)優(yōu)異。經(jīng)實驗證明,麻雀搜索算法(sparrow search algorithm, SSA)的啟發(fā)來源于自然界中的麻雀覓食過程。相對于其他智能優(yōu)化算法,SSA在迭代時間、尋優(yōu)精度以及穩(wěn)定性方面表現(xiàn)得更加優(yōu)異。基于此,首先應用主成分分析法對卡鉆數(shù)據(jù)進行主成分的提取,然后建立ISSA優(yōu)化SVM的卡鉆預測模型,以提高對卡鉆事故的預測準確性。研究成果可有效防范鉆井過程中可能發(fā)生的重大事故,保護工作人員的安全和鉆井設(shè)備的完整性,提高鉆井作業(yè)效率。

1 麻雀搜索算法(SSA)

SSA是通過模仿自然界中麻雀的捕食和反捕食行為而得到的一種算法。群體中麻雀分為3種類型：發(fā)現(xiàn)者、追隨者和警戒者。發(fā)現(xiàn)者獲取食物的位置信息,并將其提供給整個麻雀群體。追隨者在得知發(fā)現(xiàn)者提供的位置信息后去獲取食物,并監(jiān)視其他想要獲取食物的發(fā)現(xiàn)者。根據(jù)不同情況,發(fā)現(xiàn)者和追隨者的角色可以自由切換。當麻雀群體在覓食時,警戒者會發(fā)現(xiàn)危險并發(fā)出警告,一旦群體收到警告,就會立即采取反捕食行為[7]。

發(fā)現(xiàn)者位置更新由式(1)獲得。

(1)

追隨者按式(2)進行位置更新。

(2)

警戒者根據(jù)式(3)進行更新位置。

(3)

2 支持向量機(SVM)

SVM可用于線性可分問題的分類,通過找到最優(yōu)超平面使數(shù)據(jù)點完全分離,并使距該平面最近的數(shù)據(jù)點到該平面距離最大[10]。這可以解決下述最優(yōu)化問題。

(4)

式(4)中：i=1,2,…,l;ξi為松弛變量因子,ξi≥0;xi為第i個樣本;yi為分類類別;ω為垂直于超平面的向量;b為偏移量;C為懲罰因子,當出現(xiàn)錯誤分類時C就會增大。

引入拉格朗日函數(shù)以求解式(4),即

(5)

式(5)中：α為拉格朗日方程的系數(shù)因子構(gòu)成的向量;αi為拉格朗日方程的系數(shù)因子。

對式(5)中的ω和b分別求偏導,并令其等于0,解得式(4)的對偶問題,具體為

(6)

進一步解得,線性情況下的決策函數(shù)為

(7)

使用核函數(shù)將樣本數(shù)據(jù)映射到高維空間,可以將一般非線性問題變?yōu)榫€性可分,核函數(shù)的表達式為

K(xi,xj)=φ(xi)φ(xj)

(8)

式(8)中：φ(xi)為將xi映射后的特征向量;φ(xj)為將xj映射后的特征向量。

徑向基核函數(shù)表達式為

(9)

式(9)中：g為核參數(shù)。

同理,非線性情況下的決策函數(shù)得到如式(10)表達式,具體為

(10)

綜上,使用SVM解決分類問題時,懲罰因子C和核參數(shù)g是影響分類結(jié)果的重要因素。

3 主成分分析法(PCA)

PCA本質(zhì)上是一種提取數(shù)據(jù)特征的方法,它可在保留原有數(shù)據(jù)所包含信息基礎(chǔ)上,降低數(shù)據(jù)維度,提高運算效率。利用PCA對鉆井過程中收集的高維數(shù)據(jù)做降維處理,可減少數(shù)據(jù)冗雜造成的影響[11]。

假設(shè)存在n個樣本數(shù)據(jù),每個樣本有p個指標變量,則可構(gòu)建樣本矩陣X,即

(11)

對式(11)中的樣本矩陣X進行變換,PCA步驟如下。

步驟1對樣本矩陣X中的每一個元素xij按照式(12)做標準化處理,具體為

(12)

步驟2根據(jù)標準化矩陣,得到相關(guān)系數(shù)矩陣R,即

(13)

步驟3計算式(13)中矩陣R的p個非負特征值,且滿足λ1≥λ2≥…≥λp,以及對應的特征向量μ1,μ2,…,μp,重新構(gòu)建線性關(guān)系,其表達式為

(14)

式(14)中：f1為第1主成分;f2為第2主成分;fp為第p個主成分;xp為第p個主成分的原始特征;μnp為第p個主成分中第n個特征系數(shù)。

步驟4計算主成分fj(j=1,2,…,p)的方差貢獻率aj和累計方差貢獻率bp,其計算公式分別為

(15)

式(15)中：λj為第j個主成分的方差;λi為i個主成分的總方差。

步驟5選取主成分個數(shù)。m(m≤p)個主成分的累計方差貢獻率越接近100%,說明該m個主成分可以代表原始數(shù)據(jù)的信息[12]。

4 改進麻雀搜索算法(ISSA)

ISSA是種群智能優(yōu)化算法,仍存在當算法搜索到全局最優(yōu)解時,種群會趨于單一,導致難以跳出局部最優(yōu)的限制問題。

4.1 自適應非線性慣性遞減權(quán)重

研究指出,慣性權(quán)重參數(shù)在增強全局搜索能力和跳出局部最優(yōu)方面起著重要作用。將此策略引入到發(fā)現(xiàn)者位置更新公式中,從而獲得自適應非線性慣性遞減權(quán)重ω的計算公式為

(16)

式(16)中：t為迭代次數(shù);tmax為最大迭代次數(shù);ω1和ω2為慣性調(diào)整參數(shù),取ω1=0.9,ω2=0.4。

引入慣性權(quán)重ω后,發(fā)現(xiàn)者按照式(17)進行位置更新,具體為

(17)

式(17)中：i為第i只麻雀。

根據(jù)式(16)可知,在迭代初期,自適應非線性慣性遞減權(quán)重緩慢衰減,有利于全局搜索,可更好地確定最優(yōu)解位置。而在迭代后期,衰減迅速,有利于局部搜索,可縮短尋找最優(yōu)解的時間[13]。

4.2 萊維飛行策略

萊維飛行策略(Levy Flight)適用于隨機搜索,尤其是距離較短或隨機距離較長的情況,通過進行更充分的全局搜索和局部搜索,可以使算法在尋找最優(yōu)解時更為全面,同時更容易避免陷入局部最優(yōu)的局限[14]。

Levy Flight的計算公式為

Lef=0.01s

(18)

式(18)中：Lef為萊維飛行路徑;s為Levy Flight飛行步長,計算公式為

(19)

(20)

式(20)中：β一般取值為1.5。

σv=1

(21)

引入Levy Flight后,警戒者按式(22)更新位置,可表示為

(22)

5 ISSA性能測試

為驗證ISSA在求解目標函數(shù)極值問題中的優(yōu)越性及可行性,將ISSA與遺傳算法(genetic algorithm,GA)、SSA、灰狼算法(grey wolf optimizer,GWO)在8個基準測試函數(shù)上進行對比測試。

5.1 基準測試函數(shù)

表1為測試函數(shù)表達式,從高維和低維對算法跳出局部最優(yōu)的性能進行測試[15]。

表1 基準測試函數(shù)Table 1 Benchmark test functions

5.2 算法性能對比分析

為增強實驗結(jié)果可信度、避免偶然誤差,實驗針對8種基準測試函數(shù)進行30次獨立運行,使用30作為種群維度,最大迭代次數(shù)為1 000。實驗結(jié)果如表2所示,平均值和標準差為評價指標。

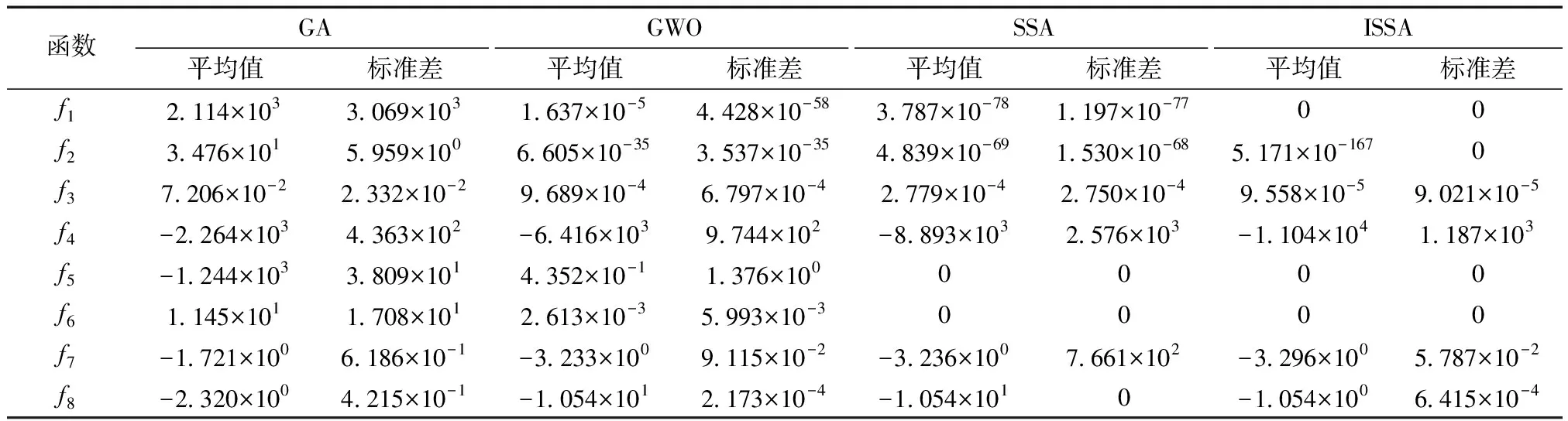
表2 基準函數(shù)優(yōu)化結(jié)果比較Table 2 Comparison of optimization results of benchmark functions

由表2可知,在f1～f3高維單峰函數(shù)測試中,相較于其他算法,ISSA的尋優(yōu)精度與穩(wěn)定性均顯著提升,且平均值和標準差提升了至少2個數(shù)量級;在f4～f6高維多峰函數(shù)測試中,ISSA的尋優(yōu)能力相較于其他算法有顯著的提升,且求解f5和f6時,ISSA和SSA的平均值和標準差均為0,為它們尋優(yōu)能力相同。在測試低維函數(shù)f7～f8中,ISSA仍明顯優(yōu)于其他算法。綜上,在單峰和多峰、高維和低維函數(shù)上,ISSA相對于其他算法,其求解精度有所提升,算法穩(wěn)定性也更優(yōu)。

6 ISSA-SVM的卡鉆預測模型

6.1 PCA卡鉆數(shù)據(jù)降維

實驗所用的卡鉆數(shù)據(jù)來自國外某大型油田,此油田共收集有1 600組數(shù)據(jù)記錄。其中,400組為發(fā)生壓差卡鉆(differential stuck, DS)時的鉆井數(shù)據(jù);400組為發(fā)生機械卡鉆(mechanical stuck, MS)時的鉆井數(shù)據(jù);400組為正常情況(non-stuck, NS)的鉆井數(shù)據(jù)。數(shù)據(jù)記錄共有10維特征,分別為：測深、泥漿比重、鉆頭大小、排量、初切力、終切力、扭矩、機械鉆速、轉(zhuǎn)盤轉(zhuǎn)速和鉆壓。使用PCA對10個特征做降維處理,提取出的主成分方差貢獻率和累計方差貢獻率如圖1所示。由于在10個特征信息中,3個主成分累計方差貢獻率達到了88.841%,提取大于3個主成分,累計方差貢獻率增長趨勢變緩,即原始鉆井數(shù)據(jù)的10個特征信息經(jīng)PCA處理后大多集中在這3個主成分上,因此本次使用PCA卡鉆數(shù)據(jù)降維選擇提取3個主成分。部分卡鉆數(shù)據(jù)如表3所示。

圖1 主成分貢獻率

表3 部分樣本數(shù)據(jù)Table 3 Selected sample data

6.2 ISSA預測SVM流程

為預測卡鉆事故,通過ISSA對SVM的懲罰因子C和核參數(shù)g進行優(yōu)化。其優(yōu)化流程圖如圖2所示[16]。

圖2 ISSA-SVM流程圖

6.3 ISSA預測SVM的卡鉆預測實現(xiàn)

對卡鉆數(shù)據(jù)降維提取出的3個主成分,按照7∶3的比例將DS、MS和NS的數(shù)據(jù)分成訓練集和測試集進行卡鉆事故的分類預測。建立ISSA-SVM、SSA-SVM、GWO-SVM和GA-SVM的分類預測模型。這4種算法分類預測的適應度曲線如圖3所示。其中,最大迭代次數(shù)為100次,種群數(shù)量為20。

紅實線為每次迭代的最佳適應度值;藍色虛線為每次迭代的種群平均適應度值

從圖3可以看出,為達到分類準確率的最佳適應度,ISSA-SVM僅需迭代10次達到85.185 2%的最佳適應度值。而SSA-SVM和GA-SVM則需要分別迭代23次和24次。GWO-SVM僅需迭代2次就可達到75.185 2%的最佳適應度數(shù)值,但最佳適應度數(shù)值小于ISSA-SVM。相較于其他優(yōu)化算法,ISSA能更快速、精確的找出SVM的懲罰參數(shù)C及核參數(shù)g。

將4種算法分別用于優(yōu)化SVM的C和g,構(gòu)建卡鉆分類預測模型,如圖4所示。

圖4 ISSA-SVM分類結(jié)果圖

4種算法的卡鉆事故分類結(jié)果如表4所示。通過4種算法的對比分析可知：GA-SVM和GWO-SVM卡鉆分類預測模型準確率η相同,均為75.185 2%。ISSA-SVM的預測效果最好,預測準確率可達到85.185 2%,相比于SSA-SVM、GA-SVM模型的預測準確率分別提高了0.37%、10%。結(jié)果表明,ISSA在尋找最優(yōu)參數(shù)方面速度快,分類預測準確率也更高,即ISSA效果顯著。

表4 4種算法對比Table 4 Comparison of the four algorithms

6.4 混淆矩陣分析

使用混淆矩陣來驗證基于ISSA-SVM的卡鉆事故預測模型的準確性,并根據(jù)混淆矩陣計算出預測模型的準確率。混淆矩陣可以比較分類結(jié)果與實際值之間的誤差,評判模型分類的優(yōu)劣[17]。為了驗證準確性,對270個訓練集進行了混淆矩陣分析,并通過可視化展示結(jié)果,如圖5所示。

類別標簽0為正常情況;1為壓差卡鉆;2為機械卡鉆

如圖5所示,縱軸標簽為預測類別,橫軸標簽為真實類別,精確率為模型預測值與真實值相同所占預測值的比重,識別類型為0、1和2的精確率分別為91.1%、80%和84.4%;召回率為真實值正確的預測值所占真實值比重,分別為90.1%、84.7%和80.9%;準確率為分類中所有判斷正確的結(jié)果占總預測值的比重,為85.2%。識別類型為0、1和2時,精確度大于80.0%,總的來說,改進麻雀算法優(yōu)化支持向量機的方法應用于卡鉆事故是有效的。

7 結(jié)論

為預防鉆井卡鉆事故的發(fā)生,通過提出ISSA-SVM的方法,在位置信息中引入改進的自適應非線性慣性遞減權(quán)重和Levy飛行策略,并利用PCA對數(shù)據(jù)做降維處理,建立用于卡鉆事故預測的模型,得到如下結(jié)論。

(1)利用基準測試函數(shù)在尋優(yōu)性能上分析得,在收斂速度和尋優(yōu)精度上,ISSA相對于GA、SSA和GWO有優(yōu)勢顯著。

(2)提出ISSA-SVM模型以用于鉆井卡鉆事故的預測,并采用PCA對鉆井數(shù)據(jù)做降維處理,提取出3個主成分。結(jié)果表明：機械卡鉆、壓差卡鉆和正常情況的分類預測準確率提升至85.185 2%,相較于SSA-SVM、GWO-SVM和GA-SVM卡鉆預測模型,ISSA-SVM卡鉆預測模型在預測準確率及運算時間方面有顯著優(yōu)勢,魯棒性更好,并利用混淆矩陣來驗證基于ISSA-SVM的卡鉆事故預測模型的準確性。綜上,提出了一種可行的方法來預測鉆井卡鉆事故,該方法能夠提供技術(shù)支持,幫助鉆井過程中及時、準確地發(fā)現(xiàn)卡鉆事故,減少不必要的損失。