基于廣義S變換的高頻地波雷達(dá)電離層雜波抑制方法

王千軍,李自立

(廣西師范大學(xué) 電子工程學(xué)院, 廣西 桂林 541000)

0 引 言

利用高頻地波雷達(dá)探測大范圍、遠(yuǎn)距離的海洋表面動力學(xué)要素和低速目標(biāo)已成為一種常規(guī)手段,同時可以對專屬經(jīng)濟(jì)專區(qū)(EEZ)進(jìn)行有效監(jiān)測[1]。在海態(tài)探測時地波雷達(dá)通常采用垂直極化方式,大部分的能量沿海面?zhèn)鞑?但是由于天線的非理想零陷導(dǎo)致一部分的能量會泄露到空中,在一定條件下會被電離層反射并以多種方式返回雷達(dá)接收機(jī),形成電離層雜波干擾[2],由于電離層的非平穩(wěn)時變特性,使得回波在距離域和頻域上均有擴(kuò)展,而且電離層回波能量要高于一般海洋回波,導(dǎo)致雷達(dá)探測能力急劇下降[3]。很大程度上限制了高頻雷達(dá)的發(fā)展,因此電離層干擾抑制方法的研究是一項重要的課題。目前最常用的自適應(yīng)波束形成算法通過在期望信號方向形成主瓣消除來自天頂方向的電離層雜波[4-5]。但是其要求天線可以形成較深且寬的零陷,而小口徑的寬束雷達(dá)是不適用的。極化濾波需要采集垂直和水平極化通道數(shù)據(jù)再進(jìn)行對消處理,因而需要多個天線也不適合小口徑便攜式雷達(dá)[6]。閾值法和正交投影法則通過假設(shè)電離層相鄰距離元之間變化緩慢且具有高度的空間相關(guān)性去除電離層雜波[7-8]。但是可能會去除回波能量較高的目標(biāo)信號,且掃描相鄰距離元的時間間隔長,對電離層的時變性反應(yīng)較慢,最終導(dǎo)致誤差較大。

本文將廣義S變換(GST)時頻濾波算法引入到電離層干擾抑制的研究。受電離層干擾的距離元時域數(shù)據(jù)經(jīng)GST變換為分辨率合適的時頻域數(shù)據(jù),然后將時間列數(shù)據(jù)依次通過建立Hankel矩陣進(jìn)行子空間濾波,去除其中的電離層干擾。

1 電離層雜波的特性

電離層通常根據(jù)太陽輻射對不同高度和成分的空氣分子電離分為D層、E層、F層三層[9]。位于最底層的D層,只出現(xiàn)在白天,離子濃度較低,臨界頻率遠(yuǎn)遠(yuǎn)小于高頻雷達(dá)的電波發(fā)射頻率,對高頻電波的反射能力不強(qiáng)。位于90 km～120 km高度的E層通常比較穩(wěn)定,但是有時會出現(xiàn)突變的Es(Sporadic E-layer)層,由于較高的電子濃度,會對高頻信號產(chǎn)生嚴(yán)重影響,使得高頻雷達(dá)在此距離范圍內(nèi)無法正常工作,是電離層干擾抑制的主要對象。位于200 km以外的F層是受太陽影響最大的區(qū)域。但是由于本文用于海態(tài)監(jiān)測的高頻地波雷達(dá)有效工作距離為100 km,F層高度遠(yuǎn)遠(yuǎn)超過了中程高頻雷達(dá)的探測距離,故不在本文考慮范圍之內(nèi)。

電離層雜波能量通常大于天線接收的海面回波能量,導(dǎo)致海面回波頻譜的噪聲基底抬高,嚴(yán)重影響了海洋表面動力學(xué)參數(shù)的提取,限制了高頻雷達(dá)的探測性能。傳統(tǒng)的時頻分析僅主要運(yùn)用短時傅里葉變換或者小波變換的方法,但是由于時間分辨率或多普勒分辨率不能同時達(dá)到協(xié)調(diào)導(dǎo)致在低頻部分和高頻部分抑制失衡,無法對變換后的數(shù)據(jù)進(jìn)行處理[10]。而本文通過GST方法緩解了失衡問題,彌補(bǔ)了常規(guī)時頻方法的不足。

2 GST時頻濾波的原理與運(yùn)用

2.1 S變換與廣義S變換(GST)

將高頻地波雷達(dá)接收的包含電離層雜波干擾的信號表示為離散時間序列

x(n)=s(n)+d(n)

(1)

式中:s(n)為海面雷達(dá)回波信號;d(n)為電離層回波信號,即需要去除的干擾信號。

根據(jù)Stockwell[11],S變換的公式可定義為

(2)

式中:x(t)表示時域中的信號;f代表信號的頻率;τ表示時間窗的中點位置,即時移因子。其中S變換的高斯窗函數(shù)為

(3)

由于高斯窗函數(shù)與r和f有關(guān),在高時間分辨率處頻率分辨率較低,在低時間分辨率處頻率分辨率較高。這樣就滿足了快速變化的信號有較好的時間分辨率而較慢變化的信號有較好的頻率分辨率。解決了STFT的缺點,這點與小波變換相同,但是其基本小波函數(shù)為

(4)

可見此小波函數(shù)不需要滿足容許性條件,因此可以將S變換看做相位校正后的小波,或者加了高斯窗函數(shù)的STFT。但是式(2)中時頻寬度無法調(diào)整,當(dāng)處理信號的變化時無法靈活改變,導(dǎo)致使用受限。因此,文獻(xiàn)[12-13]對式(2)進(jìn)行修改,加入高斯窗調(diào)節(jié)函數(shù)

(5)

進(jìn)而到了廣義S變換

(6)

式中:可調(diào)節(jié)因子λ和β為常數(shù),且λ,β>0。當(dāng)λ和β同時為1時,即為標(biāo)準(zhǔn)的S變換;在β的值固定時,當(dāng)λ>1時,時窗寬度和頻率變化成負(fù)相關(guān),而當(dāng)λ<1時,時窗寬度和頻率變化則成正相關(guān);當(dāng)β≠1時,窗函數(shù)與β成對應(yīng)指數(shù)關(guān)系。GST通過加入兩個可調(diào)節(jié)因子,調(diào)整時間分辨率和頻率分辨率,可以根據(jù)具體處理數(shù)據(jù)進(jìn)行調(diào)節(jié),達(dá)到最優(yōu)的效果。

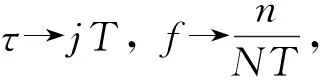
(7)

(8)

處理后數(shù)據(jù)通過廣義離散S逆變化再轉(zhuǎn)換為時域信號的實現(xiàn)公式為

(9)

式中:T為雷達(dá)采樣周期;N為雷達(dá)掃頻個數(shù);m,n和j分別為時間頻移因子,頻率值和時間窗中點位置的離散序號。

2.2 GST時頻濾波應(yīng)用

對受電離層干擾的第i距離元一維距離向信號si(n)調(diào)節(jié)(λ,β)參數(shù),通過GST變換將si(n)轉(zhuǎn)換為GSTi,矩陣各列分別為對應(yīng)時間窗的信號數(shù)據(jù)。此時再將信號數(shù)據(jù)譜按列進(jìn)行IFFT得到第k時間窗數(shù)據(jù)處理后的結(jié)果為gsk。此處,將其表達(dá)為gsk=[gsk(1),gsk(2), …,gsk(L)]T,L為對應(yīng)時間窗數(shù)據(jù)長度,(·)T表示轉(zhuǎn)置。接下來單獨(dú)對每一gsk列進(jìn)行子空間濾波去除電離層雜波干擾。

1)將gsk按照時間延時嵌套構(gòu)成Hankel矩陣,得到空間矩陣Hk。

(10)

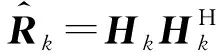
(11)

3)電離層雜波干擾序列dk(n)重構(gòu)。常規(guī)方法是將對角元素平均法[14]。用副逆角線的均值代替該副逆角線的所有元素,如此重復(fù),所有逆對角線的第一個數(shù)字就構(gòu)成了干擾序列dk(n)。但在實踐中發(fā)現(xiàn)可以使用更簡化的二值平均法,能夠在對結(jié)果影響不大的條件下,減少運(yùn)算量,提高運(yùn)行速率。

(12)

4)去電離層干擾雷達(dá)時域信號重構(gòu)。將式(12)得到的干擾信號序列從原序列中除去,達(dá)到抑制的效果。公式如下

s(n)=x(n)-dk(n),n=1,2,…,N

(13)

3 實測數(shù)據(jù)處理與分析比較

本文使用的是工作頻率為13 MHz用于海南香水灣海態(tài)監(jiān)測的便攜式高頻地波雷達(dá)回波數(shù)據(jù)。本文選取2008年1月15日11∶31雷達(dá)回波數(shù)據(jù)進(jìn)行電離層雜波抑制的研究。圖1為含電離層干擾的雷達(dá)回波頻譜,雷達(dá)距離分辨率為4 km,周期掃頻數(shù)為512。

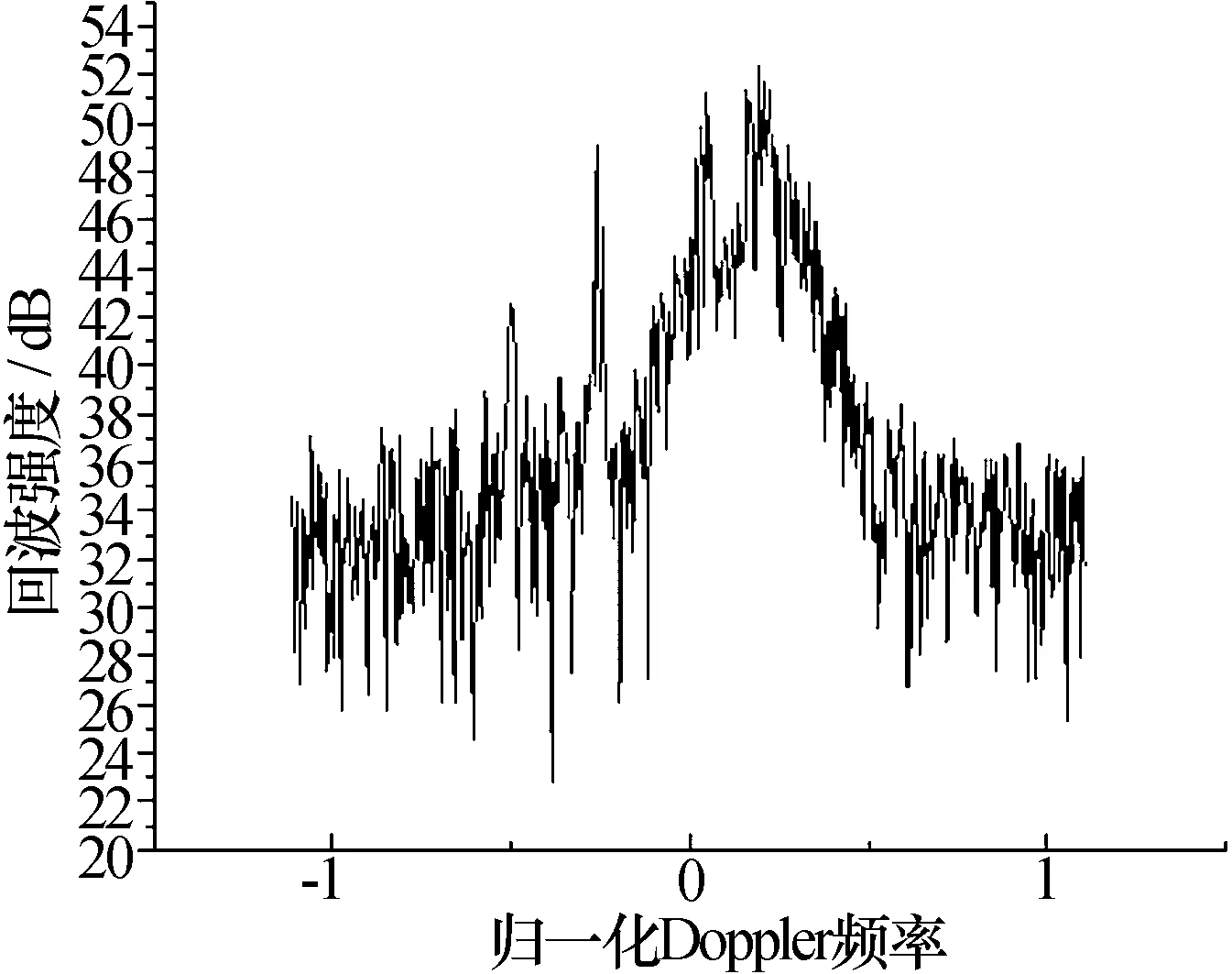
圖1 含電離層干擾的雷達(dá)回波頻譜Fig.1 Radar return spectrum with ionospheric interference

3.1 時頻圖效果分析與對比

本文通過繪制第23距離元的雷達(dá)回波數(shù)據(jù)對比分析短時傅里葉變換(STFT)和廣義S變換(GST),如圖2和圖3,橫坐標(biāo)為時間,縱坐標(biāo)為歸一化多普勒頻率。STFT使用的是漢明窗,窗長為128。為了減少頻率泄露,重疊長度為120。GST中參數(shù)設(shè)置為λ=0.8,β=1。

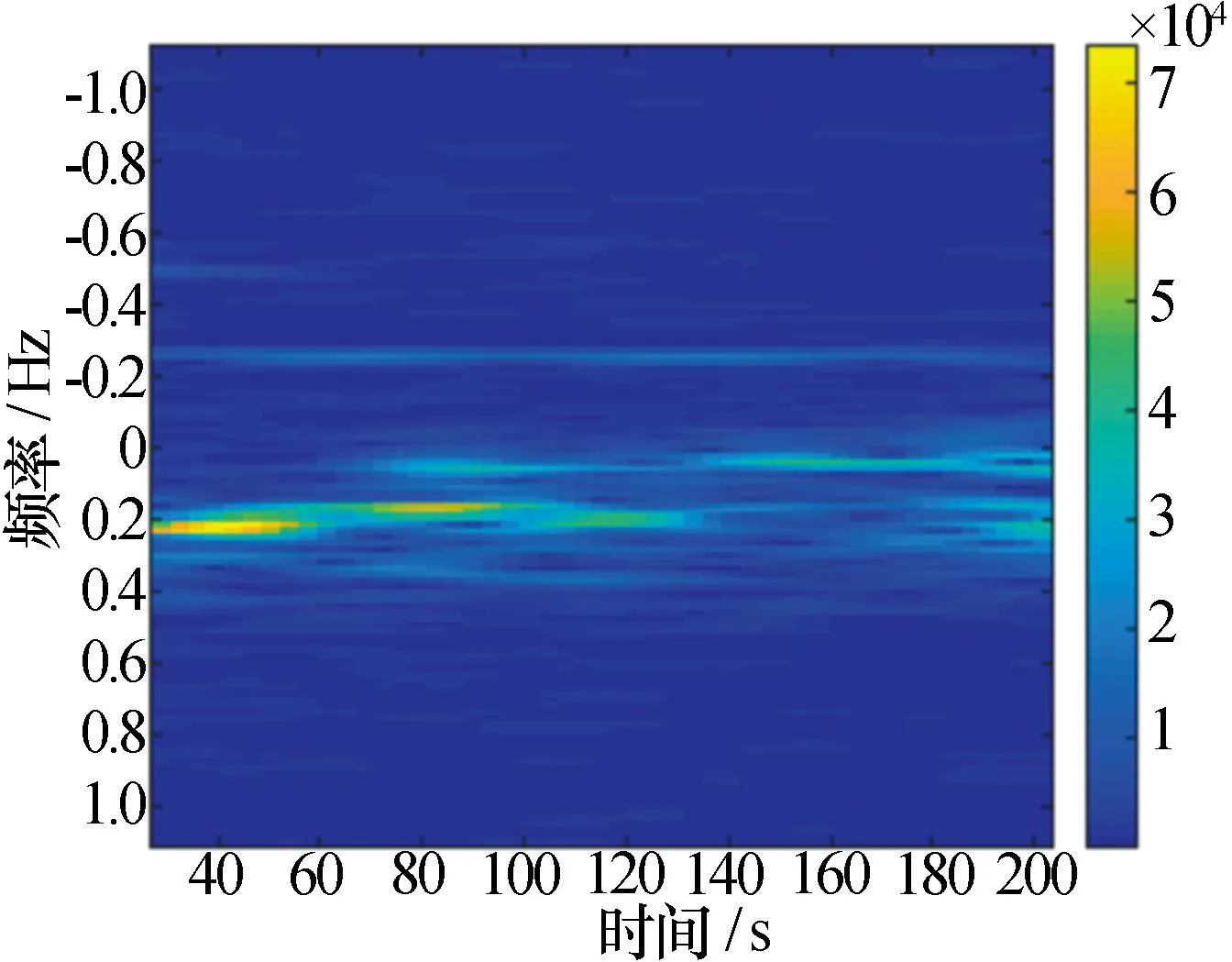
圖2 STFT的雷達(dá)回波時頻表示Fig.2 Time frequency representation of STFT radar echo

圖3 GST的雷達(dá)回波時頻表示Fig.3 Time frequency representation of radar echo of GST

圖2為 128組時間和49組頻率數(shù)據(jù)組成,只能觀察到電離層雜波對雷達(dá)回波影響的趨勢,用于粗略的分析。且時間分辨率和頻率分辨率失衡嚴(yán)重,0頻附近的固定目標(biāo)和電離層干擾頻帶之間本應(yīng)該有低干擾頻帶,但是圖一沒有顯示出來。這樣導(dǎo)致之前電離層干擾抑制只能在時頻域進(jìn)行分析,使用時頻域數(shù)據(jù)進(jìn)行處理誤差很大,一般無法使用。圖3由500多組時間和頻率組成,擁有比圖2更高的時間分辨率和頻率分辨率,且大大緩和了時間和頻率分辨率之間失衡問題。

圖3中是電離層雜波聚集區(qū)的時頻表示,主要聚集在正多普勒頻率區(qū),表現(xiàn)為多分量調(diào)幅-調(diào)頻(FM-AM)信號的形式。頻率區(qū)間0.13 Hz～0.40 Hz全時段出現(xiàn)了較強(qiáng)的電離層干擾,能量遠(yuǎn)遠(yuǎn)高于正常海浪一階回波,致使右側(cè)海浪一階峰被淹沒,且隨時間呈現(xiàn)“S”波動,這與電離層行進(jìn)式擾動(TID)相符合。高于0.4 Hz的區(qū)間,會有偶發(fā)性電離層干擾,符合電離層時變特性,而這一點在圖2中沒有體現(xiàn)。電離層雜波在相鄰時間窗的相關(guān)系數(shù)可達(dá)到0.9左右,雖然在第40 s、76 s時間上相關(guān)系數(shù)有所下降,但是對整體影響較小。而正常的海洋回波在時間域上的相關(guān)性僅有0.6左右。因此可以使用GST后的數(shù)據(jù)做時頻濾波去除電離層雜波干擾。

3.2 電離層雜波抑制

用上述方法進(jìn)行時頻域信號子空間濾波,圖4為圖3中數(shù)據(jù)經(jīng)處理后的時頻圖。正頻率區(qū)間側(cè)因未受電離層干擾得以保留,負(fù)頻率區(qū)間中雜波能量集中的區(qū)域均得到去除,保留下能量較小的目標(biāo)回波數(shù)據(jù)。

圖4 電離層雜波抑制后的時頻圖Fig.4 Time frequency map after ionospheric clutter suppression

將本文算法與距離域特征分解[15]處理兩組不同的實驗數(shù)據(jù)進(jìn)行對比,結(jié)果如圖5所示。在圖5a)中,對于GST時頻濾波方法,0.13 Hz～0.40 Hz區(qū)間的電離層雜波得到有效抑制,抑制當(dāng)量達(dá)到10 dB,且原先被淹沒的正側(cè)一階峰也得以顯露,電離層干擾頻率內(nèi)噪聲基底變得平緩。負(fù)頻率側(cè)通過時頻圖分析可知沒有受到電離層干擾,而時頻濾波幾乎沒有對此區(qū)域進(jìn)行處理,保證此區(qū)域目標(biāo)信息的完善,其中船只信號也得到了很好的保留。在圖5b)中正頻率區(qū)間未受電離層干擾,算法很好地識別并加以保留,負(fù)一階峰顯露同時還保留著較強(qiáng)的回波能量,對海洋動力學(xué)參數(shù)的十分有利。

圖5 電離層抑制前后多普勒譜Fig.5 Doppler spectrum before and after ionospheric suppression

而基于特征分解的去干擾方法,雖然電離層干擾區(qū)域得到了抑制,但是全頻域信號強(qiáng)度都遭到了削弱,一階峰附近仍有很強(qiáng)的干擾導(dǎo)致辨識難度加大,未受干擾的一階峰也被減弱,這些對后續(xù)處理的計算都是極其不利的,特別是浪高譜與一階峰強(qiáng)度直接相關(guān),這會導(dǎo)致錯誤的發(fā)生。而在圖5a)中負(fù)頻率區(qū)間的船只信息也被去除,影響了雷達(dá)的正常工作。

4 結(jié)束語

本文針對便攜式海態(tài)監(jiān)測高頻地波雷達(dá)的電離層干擾,引入GST方法,以緩和傳統(tǒng)短時傅里葉變換中時頻分辨失衡問題,使用變換后的數(shù)據(jù)進(jìn)行子空間濾波解決了傳統(tǒng)距離域特征分解誤差較大的問題。用實際數(shù)據(jù)驗證了本文方法的可行性和有效性,為電離層干擾抑制提供了新的思路。