高速鐵路動檢車軸箱加速度與輪軌力數據里程對齊研究

李王逸嘉，李晨鐘，何 慶，王 平，楊 飛，吳維軍

(1.西南交通大學 土木工程學院，四川 成都 610031；2.西南交通大學 高速鐵路線路工程教育部重點實驗室，四川 成都 610031；3.中國鐵道科學研究院集團有限公司 基礎設施檢測研究所，北京 100081；4.南昌大學 機電工程學院，江西 南昌 330031)

保持高速鐵路(以下簡稱“高鐵”)的高平順性對行車安全具有重要意義。在高鐵工務運維工作中,開展定期的軌道動態檢測是指導軌道養護維修工作的前提和基礎[1]。軌道動態檢測主要包括軌道幾何與車輛各部件動態響應兩個方面,其中軌道幾何指標包括高低、水平、軌距、軌向、扭曲等,車輛動態響應指標包括車體垂向/橫向振動加速度、軸箱垂向/橫向振動加速度、輪軌作用力等。這些指標可以從軌面平整度、線型平順性[2]、軌道彈性變形度及乘車舒適度等多個方面反應軌道的運營狀態。

目前基于軌道幾何的評價方法主要包括峰值扣分法和軌道質量指數法(track quality index,TQI)。前者僅關注超限點峰值與數量,難以反映軌道區段平均質量狀態[3-4];TQI法關注評價區段所有測點的幅值,彌補了峰值扣分法的不足,但需要人工排除因電力、環境等因素造成的數據異常[5]。與此同時,受限于設備檢測精度,兩種方法均無法反映幅值極小的短波不平順類型(例如微米級的波浪形磨耗)。

相比于軌道幾何數據,軸箱加速度、輪軌力數據因其高頻采樣的特性可以更全面地反應軌道下部短波不平順,彌補現有評價方法在短波不平順檢測中的不足。目前所使用的輪軌力數據一般通過測力輪對獲取[6-7],但測力輪對造價昂貴且容易損壞。而軸箱作為測量點位相對穩定,軸箱加速度更易直接通過傳感器跟車采集[8-10],所需費用較低且耐用性強。

為了減少測力輪對的使用,降低數據獲取成本,國內外多位學者[11-14]正致力于使用軸箱加速度對輪軌力進行預測。目前,以物理公式推演或仿真實驗所建立的映射關系難以表征列車在真實運營條件下的復雜情況,要確立實測軸箱加速度、輪軌力數據之間的映射關系,兩種數據間高精度對齊的里程信息是重要前提。此外,運維部門通常掌握多種類型運維數據,可利用多源數據所攜帶的不同信息對數據本身進行印證和補充,例如在不平順數據TQI值超限的位置是否出現對應的軸箱加速度、輪軌力峰值;在TQI值正常區段的軸箱加速度、輪軌力數據又是否出現能量集中現象,而利用多源數據對軌道狀態進行綜合評價同樣建立在高精度對齊的里程信息的基礎上。里程誤差[15-16]的存在會使探索兩種高頻采樣數據間的映射關系的難度大幅增加,也阻礙利用多源數據對軌道狀態進行綜合評價。因此消除不同數據間的里程誤差對數據綜合分析、確立映射關系都至關重要。

目前,在軌道領域的里程修正方法僅針對軌道幾何數據,且兩列數據通常為同類數據。當軌道幾何數據存在明顯曲線特征時,可以利用主點信息進行里程修正,如文獻[17]利用曲線臺賬信息修正設備誤差,建立相關系數五點迭代法逐段修正二次偏差;文獻[18]提取直曲線交匯區域主點,基于相關系數法與二次插值將里程誤差根據主點信息全局平均化進行修正,并根據數據窗長的敏感性分析對算法進行優化;與之類似的逐區段修正算法還有最小二乘法[19-20]、灰色關聯度算法[21-22]等。此外,可以利用由焊縫引起的軌道幾何峰值特征進行誤差修正,如文獻[23]建立三次樣條插值模型提取高低不平順數據中焊縫特征位置,將其規律性特征作為窗長選擇的參考值,結合均一閾值和真實焊縫修正里程誤差;文獻[24]提取實測軌距與設計軌距數據間互相關峰值位置,利用自回歸時間模型和卡爾曼濾波器修正歷史數據里程誤差。基于動態規劃的思想,根據兩波形之間最優匹配位置下各點最短距離路徑也可以進行誤差修正,如文獻[25]采用動態規劃(DP)算法,對二維曲線進行匹配修正。文獻[26-28]提出在軌道不平順數據中提取關鍵設備信息,結合動態規劃原理建立兩次檢測數據間的最優配對模型,并以目前數據存在的最大里程誤差的倍數作為匹配窗口長度的約束求解模型;文獻[29-30]提出動態時間彎曲(DTW) 算法,以歐式距離為波形相似度度量計算最短彎曲路徑,通過對橫坐標時間軸的彎曲和變形進行里程修正。文獻[31]將互相關函數、快速傅里葉變換遞歸對齊、相關優化彎曲及動態時間彎曲方法下的幾何缺陷數據對齊效果進行對比,發現DTW在波形對齊時擁有最高的精度。

綜上所述,目前的修正模型幾乎僅適用于波形重復度高的同類型數據,鮮有學者對不同類型但相互關聯的高頻采樣數據進行里程修正,現有研究對多源數據之間里程誤差的處理仍存在以下不足:

1)部分逐區段里程修正算法需要將數據本身攜帶的曲線特征信息與線路臺賬相結合才能進行數據修正,但軸箱加速度與輪軌力數據并未攜帶曲線特征信息,無法直接通過該類模型進行修正。

2)在高采樣頻率下,數據整體或局部的里程誤差將更多次積累,修正模型的整體運算量呈數量級形式大幅度增加,以動態規劃思想進行波形修正的算法(如DP、DTW算法等)難以在龐大數據量下保持運算效率和精度,易出現波形過度變形,修正后波形失真的問題。

3)目前在鐵路數據分析領域,對于描述兩種高頻采樣數據對齊效果的量化評價方法尚存在研究空白。

基于以上研究的不足之處,本文利用窗長變化作為減小算量、提高算法精度的突破口,提出一種長、短單元窗長收斂的二階段里程誤差修正模型,針對缺乏曲線信息且高頻采樣的軸箱加速度、輪軌力數據進行修正對齊。算法的具體流程如下:

1)第一階段,利用速度信息代替“曲線特征”建立軸箱加速度、輪軌力數據之間的聯系,根據四分位數閾值界定原則提取長單元速度曲線趨勢,并利用速度變化區間初步修正兩種數據間波形錯位,極大地減少了運算量,大幅提高第二階段修正的運算效率與準確性。

2)第二階段,為避免一次性處理大量數據所帶來的波形失真問題,先對全局數據進行短單元分割,而后基于互相關匹配得到兩種數據之間的精確里程修正矩陣,該矩陣基于貪心算法思想逐區段對原始數據進行線性插值,在保留數據真實性的同時消除兩種數據間內部的里程殘差。

3)為避免高頻采樣數據發散性、隨機性的特點對幅值結果評價的影響,提出以“能量”的形式提取高頻采樣數據趨勢,對加速度、輪軌力數據修正結果進行量化評價,將原始數據、粗匹配數據以及精確里程修正后數據之間的相關性進行對比分析。

1 數據說明

使用同一列車不同車廂上不同采集系統所采集的軸箱加速度與輪軌力數據,左軸箱垂向加速度、左軌垂力原始數據分別見表1、表2。其中,n為采樣點數量。由表1、表2可知,軸箱加速度、輪軌力數據均按等時間間隔采樣,但輸出的數據中僅有里程、速度數據而缺乏時間標簽,無法直接通過速度與時間的乘積得到距離進而對波形整體漂移進行修正。此外,在等時間間隔采樣下,車輛速度一般通過里程計、光柵編碼器、應答器得到。在長距離的行車中,由于車輪磨耗、輪軌間相對滑動、編碼器故障等問題,很容易造成里程的累積誤差。如果利用列車縱向加速度積分得到速度,會存在更大的積分誤差,但由于本文數據跨度很長,以這種方式得到的距離在積分累積誤差下可能會導致新的問題。

表1 左軸箱垂向加速度原始數據

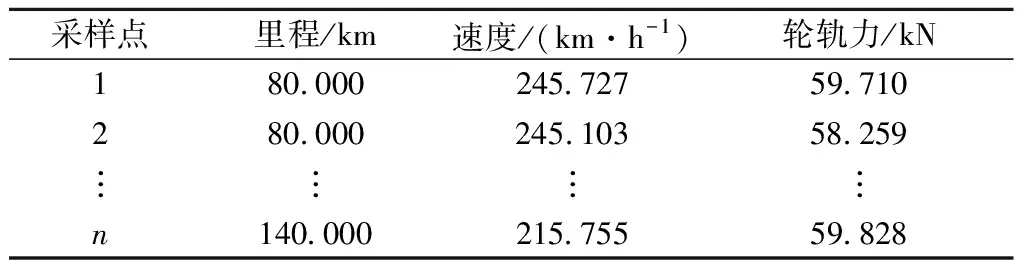
表2 左軌垂力原始數據

相比于類型相同、檢測系統一致的兩次軌道幾何數據間的里程誤差修正,不同類型的兩種數據之間的里程誤差修正將更加復雜,需要解決的問題如下:

1)缺乏曲線特征點。通常來說,用于進行里程修正的不平順數據多以超高、高低數據為主。超高指為抵消車輛在圓曲線路段上行駛時產生的離心力導致的滑移而設置的外側高于內側的單向橫坡,因此在彎道位置,超高數據必然會呈現梯形狀變化,不同時間段測得的兩次超高監測數據可根據“直緩點”“緩圓點”等曲線特征點進行校準。然而軸箱加速度以及輪軌力數據趨向于隨機分布,并不一定存在類似的數據特征點。

2)高頻采樣。通過軌檢車得到的軌道不平順數據通常以0.25 m或0.125 m進行等間距插值,屬于低頻數據。而軸箱加速度、輪軌力數據分別以5 000、2 000 Hz進行高頻采樣,在同樣的行駛距離內得到的數據總量呈數量級形式增加。

3)數據類型差異。用于匹配的軌道幾何數據往往為同類型數據,其采樣頻率、方式均相同,因此兩次數據波形之間重復度往往很高。而當匹配數據變更為加速度與輪軌力數據時,其數據類型、采集方式、采樣頻率均不同,因此采集到的兩種原始數據之間的波形匹配存在隨機性,難以做到點與點之間的對齊。

綜上所述,本文所處理的里程誤差是在多種因素的共同影響下產生的。首先,兩套采集系統位于同一列車的不同車廂,難以做到同時、同頻采樣,這是造成波形整體偏移的主要原因之一;其次,兩套采集系統本身所使用的GNSS定位系統或光柵編碼器也可能會導致里程誤差的產生;最后,由于采集的系統、頻率均不同,導致采集的數據內部存在拉伸或者壓縮的現象,以上3種因素共同影響產生了里程誤差。且由于采集系統的不同,兩數據間的里程誤差無法通過設備直接消除。若忽略該誤差對原始數據進行修正,會出現計算量太大的問題。由于缺乏曲線信息,原始波形也難以展現兩種數據之間的整體關系。

由表1、表2可知,兩套采集系統所采集到的每一個加速度、輪軌力數據都存在與之對應的速度數據。相比于波動性極強的加速度、輪軌力數據,速度數據通常在行車過程中保持穩定,速度變化時所呈現出的波動會在整體數據中尤為明顯,且其波形的重復性較高,因此,可以利用兩套系統速度波形之間的偏移量來反映軸箱加速度與輪軌力數據之間的整體偏移量。在消除波形錯位之后,再對軸箱加速度、輪軌力數據進行局部波形的收縮、拉伸處理,逐區段消除全局里程誤差。

2 基于長、短單元窗長收斂的二階段里程誤差修正模型

本文所提出模型在第一階段將軸箱加速度與輪軌力兩套采集系統中的速度數據作為里程位置參考,通過四分位數閾值界定提取速度變化長單元區段,基于長單元速度窗消除兩種高頻采樣數據間整體里程誤差。在高速列車行駛過程中,速度不斷發生波動,但通常波動范圍僅1～2 km/h,依靠四分位數法可以將速度大幅度變化區間與細小波動分離開,這種大幅波動區間在240 km/h的速度下通常會長達2 km,因此稱之為長單元。在第二階段,以輪軌力數據為基準,對軸箱加速度數據進行短單元分割,再根據互相關匹配法修正每個短單元內軸箱加速度數據,最后通過線性插值對軸箱加速度波形內部各區段進行伸縮與拼接處理,逐區段消除殘余的里程誤差。短單元的長度至少應大于軸箱加速度的一個采樣周期且包含2～5個焊縫沖擊信號在內,在240 km/h的速度下短單元長度約為150～300 m,里程誤差修正模型流程見圖1。圖1中,i為當前軸箱加速度窗口數;j為當前輪軌力窗口數;jmax為最大輪軌力窗口數。

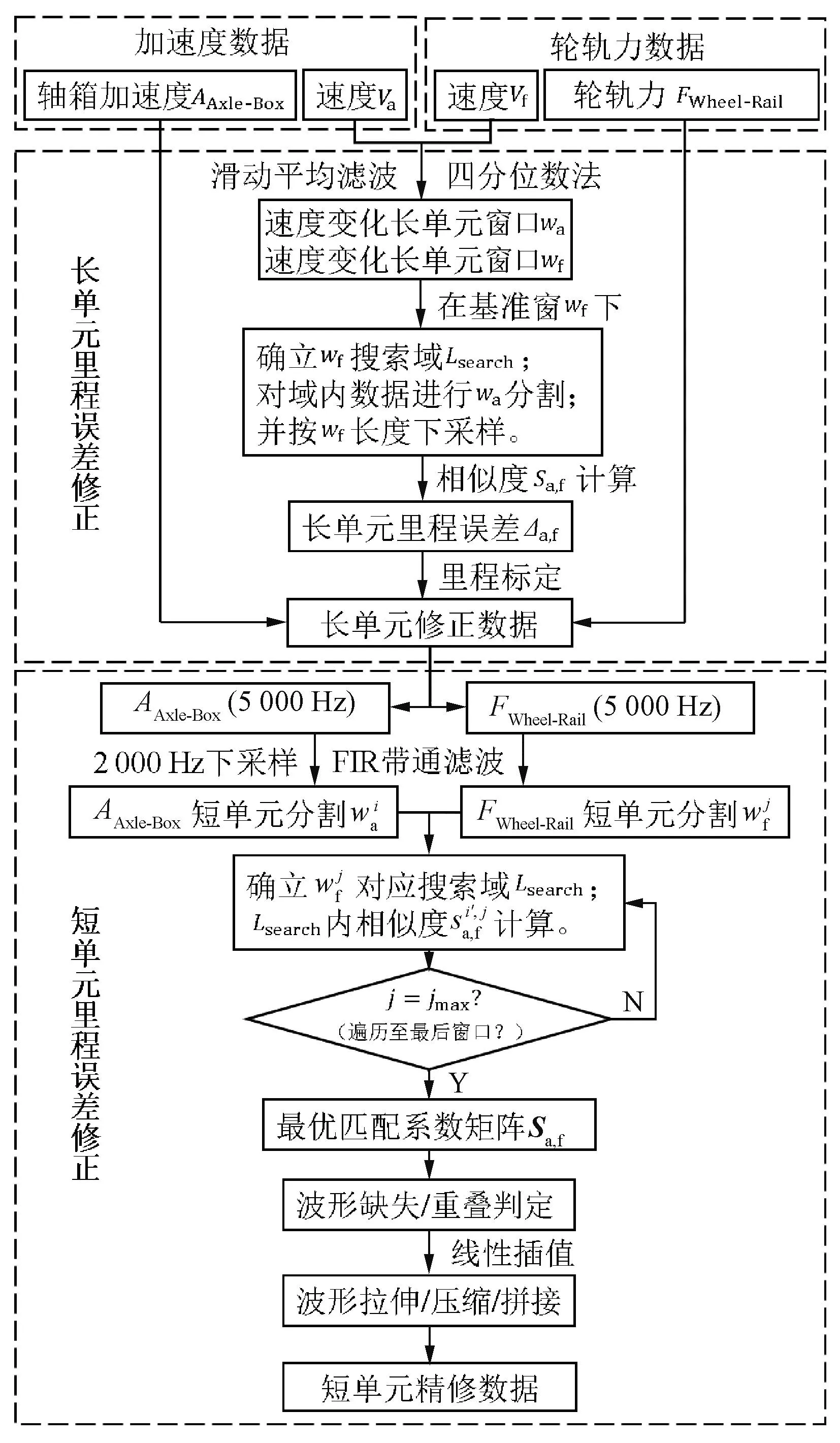
圖1 里程誤差模型示意

2.1 長單元里程誤差修正方法

四分位數閾值界定法用上、下四分位數和四分位差來定義內限、外限,將內限以外的小概率離群點視為異常值。利用上、下四分位數(總體數據從小到大排列后位于75%與25%位置的數據)Q3和Q1以及四分位差QIQR(Q3-Q1)來確定內限,內限范圍為(Q1-1.5QIQR,Q3+1.5QIQR),數據點落于內限以外的概率為0.7%,可視為小概率離群點,本文將此類數據作為速度變化區間。可根據需要,對所需QIQR的倍數閾值進行調整,從而將變化區間與細微波動分離。

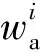
圖2 長單元里程誤差修正方法

在相似性評價計算時,需保證數據長度與形式一致,為保證變化后數據的真實性,將采樣頻率相對較低的輪軌力數據作為基準數據。按以下步驟修正長單元里程誤差。

1)基準窗口選取

將Vf數據變化區間,即輪軌力速度數據Vf與輪軌力四分位限值切割區間wf作為基準窗口,窗長為lf。

2)加速度-速度數據窗口分割

以窗長la對Va數據進行矩形窗分割處理。為保證波形之間具有更好的重復性以及相似度評價的準確性,窗與窗之間的間隔不宜過大,建議步長約為窗長的千分之一。

3)基于基準窗口長度的Va窗口數據下采樣

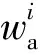
Wa={wai|i=1,2,…,n}

( 1 )

式中:ca為相鄰窗口間步長;int(·)為取整函數。

4)搜索域波形相似度計算

以基準窗口的中心里程Mf為中心,在加速度的速度數據Va中提取里程點Mf前后3倍波峰或波谷間極值點差的里程區段作為搜索域Lsearch,計算整個搜索域內加速度窗口集合相對于輪軌力基準窗口內速度波形的相似度sa,f,得到波形相似度向量Sa,f。

Lsearch=(Mf-3lcrest,Mf+3lcrest)

( 2 )

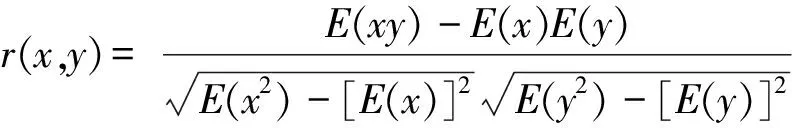
( 3 )

( 4 )

( 5 )

5)確定最優匹配窗口中心里程

將波形相似度向量Sa,f中皮爾遜相關系數最大值位置所在窗口認定為最優匹配窗口,并以此得到匹配窗口中心位置里程Ma。

6)波形錯位里程重新標定

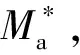
Δa,f=Mf-Ma

( 6 )

( 7 )

2.2 短單元里程誤差修正方法

通過長單元的里程標定修正后,原始數據波形的整體錯位被消除,但長單元修正并未解決數據波形局部不均勻分布的問題。因此,按以下步驟對高頻采樣的軸箱加速度、輪軌力數據中短單元里程誤差進行修正:

1)基于輪軌力基準數據采樣頻率的加速度數據下采樣與窗口劃分

在對兩種波形進行相似度計算時,需確保窗長內兩種數據采樣點數量一致,因此以基準數據的采樣頻率fs,對加速度數據進行下采樣,得到的加速度采樣點為Na,基準數據的采樣點Nf不變。

2)加速度、輪軌力數據窗口分割

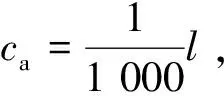
第一課時教學中，主要以人物年譜表為教學的“抓手”，讓學生在閱讀、勾畫、填表中自主學習，學生在與文本、海倫、教師充分地對話之后，發現人物小傳寫作的兩大密匙：按時間節點寫清人生軌跡；詳寫一些經歷，突出人物特點。

( 8 )

( 9 )

3)搜索域判定

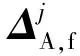
Ls,search=

(10)

4)計算以輪軌力數據窗口為基準的遍歷相似度評價矩陣

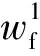
(11)

(12)

(13)

5)確定最優波形匹配矩陣

(14)

(15)

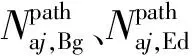
6)多次插值的短單元波形伸縮修正方法

表3 波形重疊與缺失情況表

若忽略掉區段的重疊與缺失部分,直接將匹配窗口數據進行拼接將會導致軸箱加速度波形的重復與失真,因此在數據拼接前應將缺失、重疊部分考慮在內,對加速度數據窗口進行插值伸縮,線性插值函數為

(16)

式中:xi、yi分別為原數據曲線第i點的橫坐標和原數據曲線函數值;xi+1、yi+1分別為原數據曲線第i+1點的橫坐標和原數據曲線函數值;xnew為數據曲線插值點橫坐標;ynew即xnew下數據曲線函數值。

判定與線性插值修正過程如下:

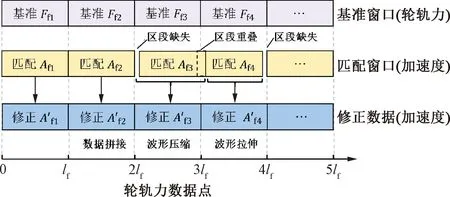
圖3 里程誤差線性插值修正方法

對加速度數據相鄰窗口進行判定規則如下:

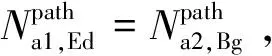
(17)

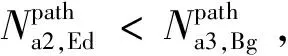
(18)

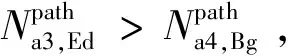
(19)

重復上述過程直至所有的匹配窗口全部轉化為修正窗口,再進行拼接形成里程誤差修正之后的軸箱加速度數據。

3 實例驗證

為驗證里程修正模型的有效性,選取某雙向東部貨運專線里程K80+000—K140+000區段的軸箱加速度、輪軌力數據進行分析。本節基于選取的數據分別進行長單元初步修正、短單元精確修正,并展示每一步修正前后的結果,最后對修正前后結果進行量化對比。

3.1 工程實例

在第一階段,用速度數據建立軸箱加速度、輪軌力數據之間的聯系,進行長單元里程修正。為提取速度波形,使用FIR濾波器進行0.1 Hz低通濾波去除原始高頻采樣產生的毛刺,再對濾波后的數據進行滑動平均處理,處理后速度數據頻數分布見圖4。由圖4可知,速度數據呈現“非正態分布”的特征。

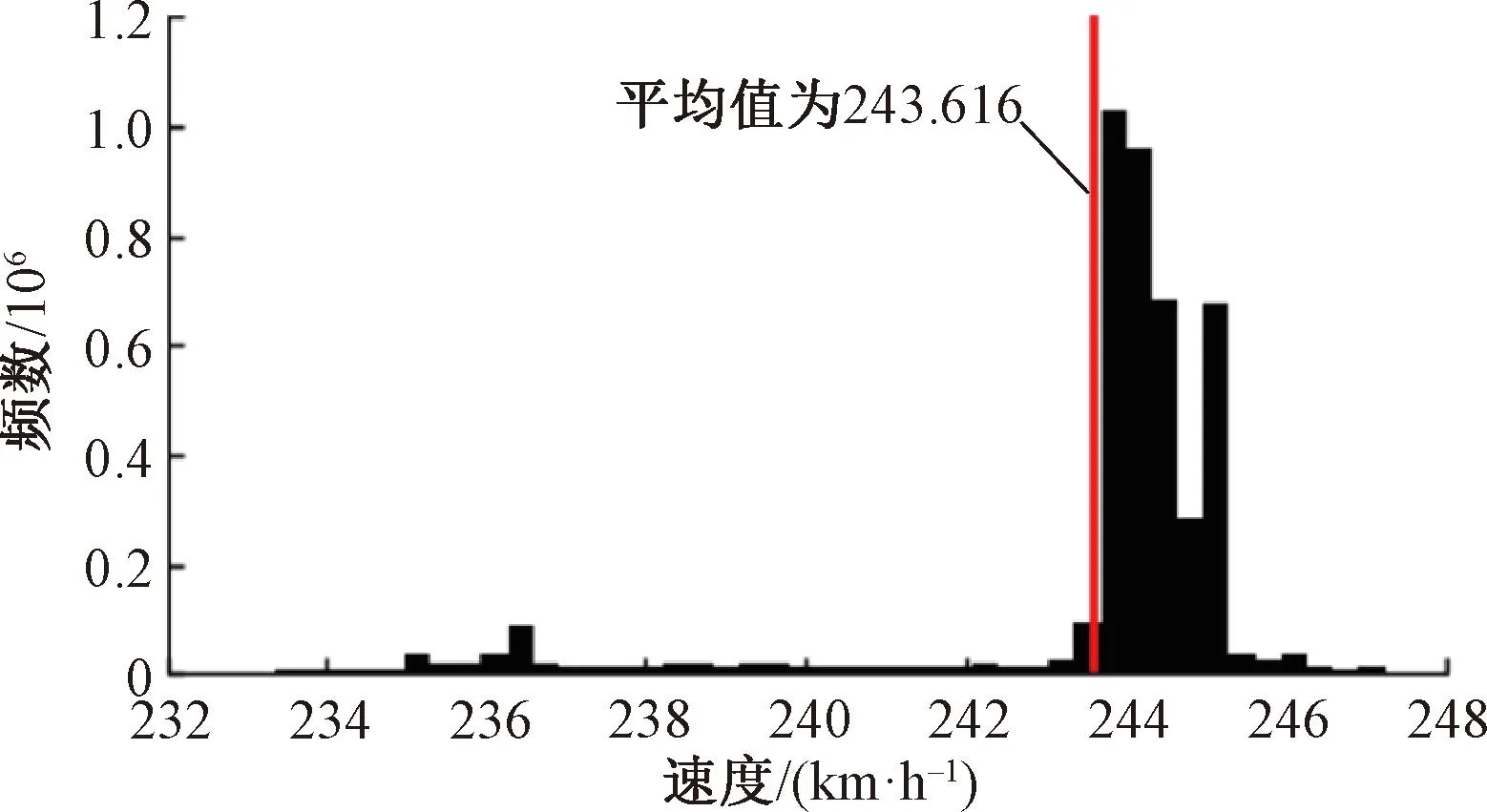
圖4 加速度、輪軌力數據速度波形及分布

為將速度細微波動與速度變化區間分離,以Q1～2QIQR為界限對原始數據進行分割,將Q1～2QIQR范圍之外的區段視為速度變化的區間,并對速度變化的閉合區域進行提取,見圖5。

圖5 四分位閾值界定判定速度變化區間原理

圖6 長單元修正前后速度圖像對比

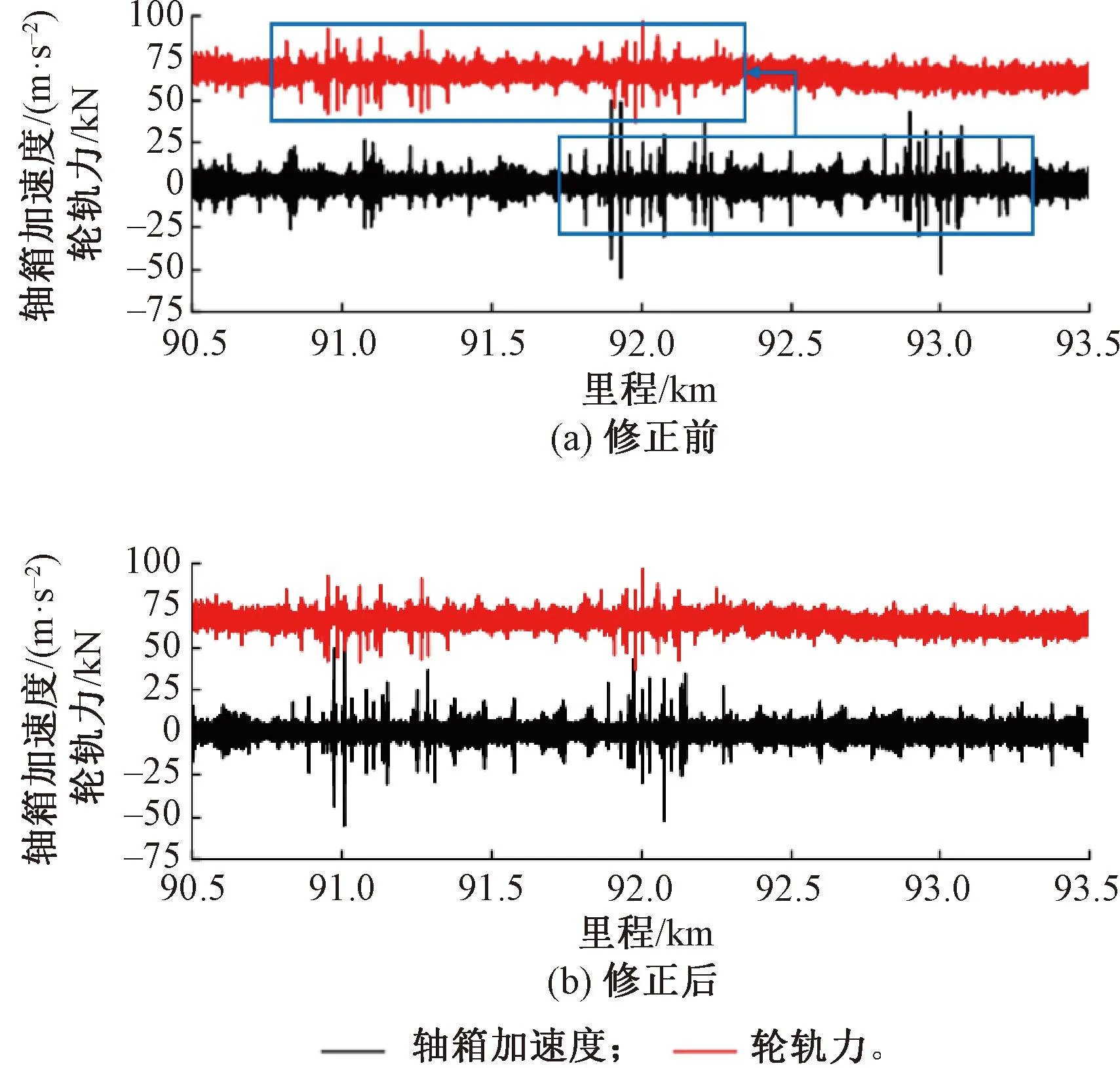
圖7 長單元修正前后軸箱加速度、輪軌力數據

軸箱加速度、輪軌力區段長單元修正前后數據見圖8。這種以長單元區間的平均誤差對整體數據進行波形平移修正的方法仍存在以下缺陷:①不能處理長單元內部的里程誤差信息;②里程誤差存在于整個修正區段內且非均勻分布,平移并不能解決兩種數據波形整體或局部的收縮、拉伸問題。前后相差近0.07 km的Δa,f表明,原始數據內部仍存在由波形伸縮造成的里程誤差,因此需要對高頻加速度、輪軌力數據進行短單元精確里程修正。

圖8 短單元修正前后軸箱加速度、輪軌力數據

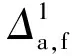
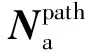
在經過第一階段的長單元修正后,兩數據任意區間相對里程誤差從1 km縮小至42 m以內;而后在經過短單元精確修正后,各區段里程誤差均值為0.32 m,在99.7%的置信度下,該線路任意區段高頻采樣數據誤差可控制在[-0.92,1.55]m。

3.2 與DTW修正效果的對比

文獻[31]已將互相關函數、快速傅里葉變換遞歸對齊、相關優化彎曲及動態時間彎曲方法下的幾何缺陷數據對齊效果進行對比,發現DTW算法在波形對齊時擁有最高的精度。因此此處將DTW算法的運行結果與本文方法進行對比。

DTW算法的修正方式見圖9,在每一步中都需要計算與之相鄰點的累積距離,并根據最短累計距離選擇最優匹配路徑。但由于本文數據量異常龐大,該累計距離矩陣將會特別冗長,再加上兩種數據具備峰值隨機出現的特點,因此在修正效率上,利用DTW算法對原數據進行修正的時間較長,接近3 h,而本文提出的二階段收斂窗長下的用時僅為DTW算法的六分之一。

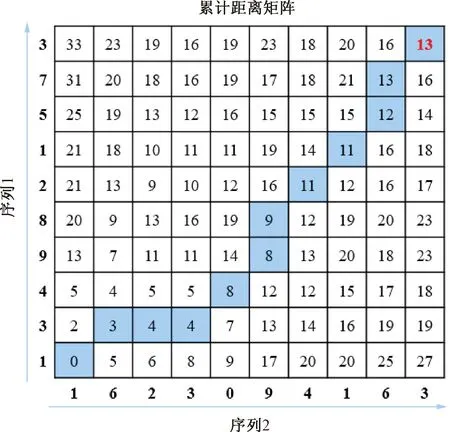
圖9 DTW算法的運作模式及累計距離矩陣

由于DTW算法會對數據的時間軸進行彎曲來對數據進行修正,因而當數據量較大時,很容易出現由于過度的拉伸、壓縮而出現的波形失真。在此隨機截取一段原始數據、經本文二階段窗長收斂算法修正后數據與DTW算法修正后的數據進行對比,見圖10。由圖10可知,DTW算法修正后的軸箱加速度數據出現了嚴重的波形失真,而本文所提出的方法可以很好地保證數據的完整性和真實性。對該段兩種算法修正結果以皮爾遜相關系數進行衡量發現,本文所提出二階段窗長收斂修正算法較DTW算法的皮爾遜相關系數提升了約5倍。

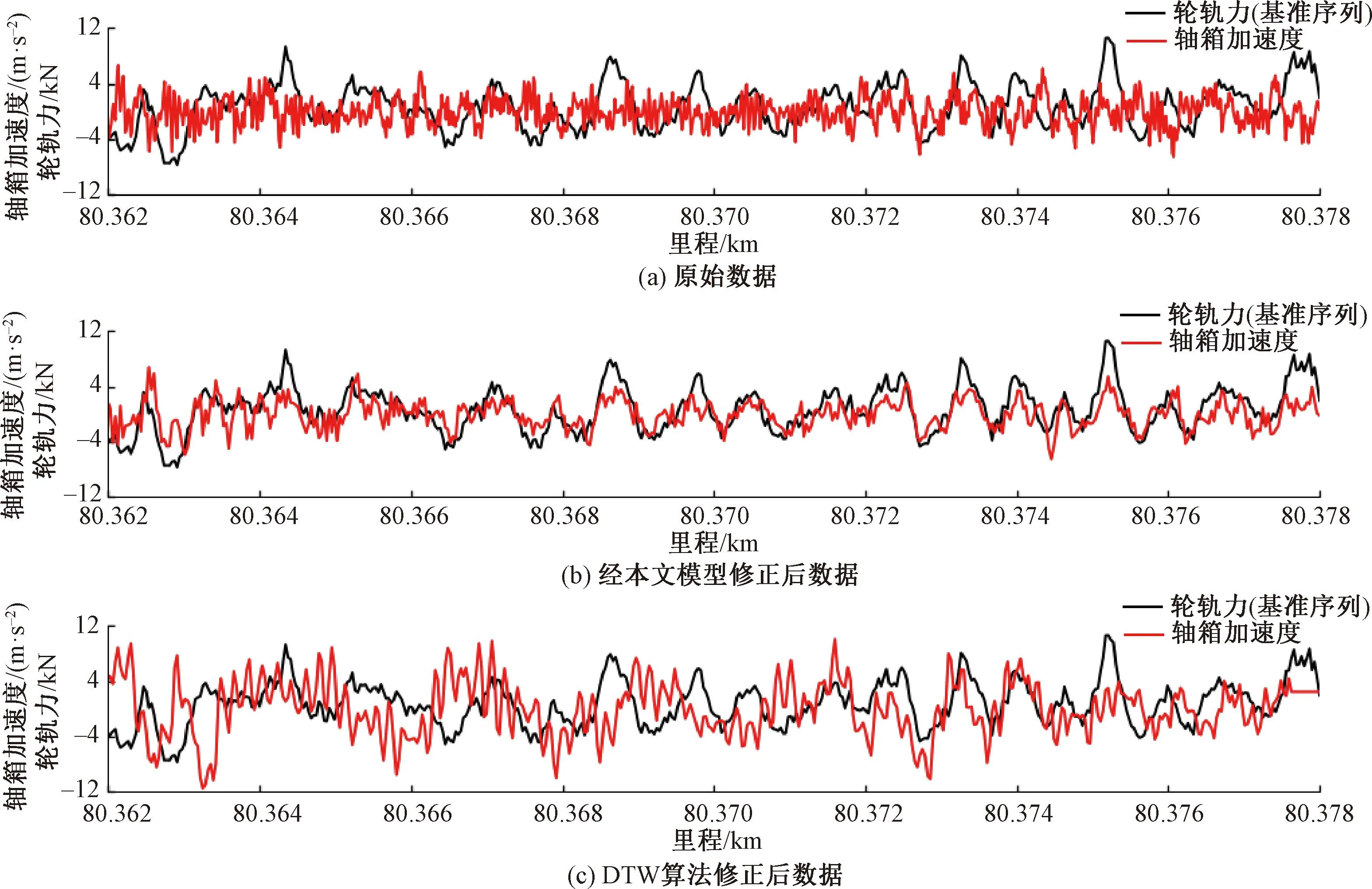
圖10 二階段窗長收斂法與DTW算法修正結果對比

3.3 基于能量累積趨勢的線性相關性評價

依據高頻采樣數據單個峰值評價存在隨機性、發散性的問題[32],但軌道高頻振動下的沖擊能量卻相對穩定,均方根值具有“能量”的概念,可用于度量軌道短波不平順引起的動態響應。軸箱加速度、輪軌力數據作為高頻采樣數據,對軌道短波不平順產生的高頻信號非常敏感,相對于點對點的峰值相似性評價,利用滑動積分窗內均方根值提取修正后的兩種數據區段能量趨勢的變化,通過對該趨勢的相似性評價來對修正效果進行衡量將更加合理。

首先對軸箱加速度、輪軌力進行數據標準化,消除數據量綱的影響,逐步計算所有數據,并分析單元內均方根值Si。

(20)

(21)

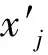
在完成均方根計算后,提取兩種數據每5 s內50個分析單元的均方根能量趨勢,進行相似度評價,結果見圖11。

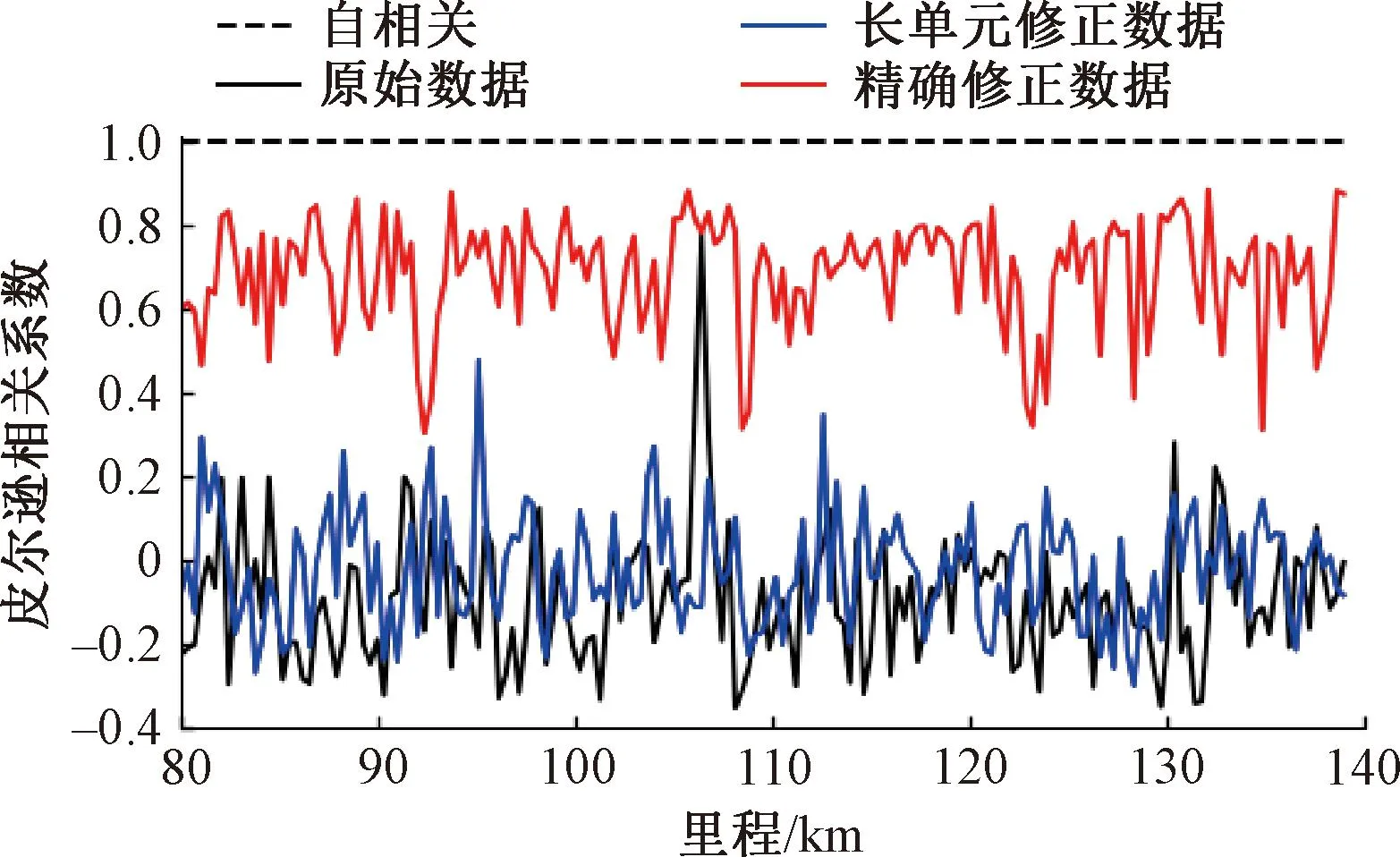
圖11 修正前后高頻采樣數據能量趨勢評價對比

由圖11可知,兩種數據的整體能量趨勢線性相關性系數從-0.079提升至0.650,且紅色曲線所代表的精確修正數據幾乎在全局任意區段均優于原始數據,表明修正模型提高了兩種數據之間的整體相關性。其中紅色曲線的極值下降點部位原始數據波動不明顯,線性相關性較低,結合臺賬數據與超高數據對比,暫排除其與彎道、橋梁段之間有直接關系,有待進一步研究。

4 結論

針對高鐵動檢數據中軸箱加速度和輪軌力數據提出基于二階段波形匹配的里程對齊算法,在減小里程誤差方面取得良好的效果。主要結論如下:

1)利用速度數據代替“曲線特征信息”建立高頻采樣數據之間的聯系,通過識別速度變化區間消除因采集系統不同導致的長里程偏移,有效提高計算效率,并提出一種全局里程插值修正方法,在避免修正過程中出現波形失真的同時保留了修正數據的真實性。

2)通過兩階段修正模型處理軸箱加速度、輪軌力數據里程誤差,在長單元修正后,兩數據任意區間相對里程誤差從1 km縮小至42 m以內;經過短單元精確修正后的兩種數據在99.7%的置信度下任意區段間的里程誤差可控制在[-0.92,1.55]m。

3)從“能量”的角度提出一種高頻沖擊數據修正前后的量化評價方法,在此方法下,原始的軸箱加速度、輪軌力數據間相關系數僅有0.07且為負相關,經過二階段修正后整體數據間相關系數達到0.65,兩高頻采樣數據間的相關性得到顯著提升。

綜上,模型將原高頻采樣數據間近1 km且分布不均的里程誤差縮小到1.55 m以內,為探究實測軸箱加速度、輪軌力之間映射關系提供基礎,對研究軌道劣化、軌道狀態智能監測具有重要意義。模型是在存在明顯速度變化區間的合理假設下成立的,但若列車在幾十公里內均未發生速度變化的極端情況,可能會降低該模型的計算效率與準確性,未來可針對速度平穩區間的里程修正方法做進一步研究,對現存不足進行改進和補充,使模型更好地服務于軌檢數據分析。