球體低速斜撞擊成坑規律試驗研究

戴立夫，凌道盛，鄭建靖，施昌宇

(1.浙江大學 建筑工程學院，浙江 杭州 310058；2.中交第二航務工程局有限公司 技術中心，湖北 武漢 430040；3.浙江大學 超重力研究中心，浙江 杭州 310058)

行星探測表明太陽系大量小天體表面覆蓋有深厚風化層，并分布有許多大小不等的類半橢球形撞擊坑.除地質效應因素外，撞擊坑主要成因為斜撞擊.天體表面通過各種撞擊事件不斷進化，除單一大規模撞擊事件外，還存在較小規模撞擊事件，例如天體表面自發噴射物質后又重新低速回落斜撞擊天體表面[1-2].探究這種小規模撞擊坑的形成能夠詳細地揭示天體表面的演變過程，也利于了解天體表面形成二次撞擊的可能性[3].探測器著陸以及執行小天體表面撞擊試驗均會形成撞擊坑，量化低速斜撞擊成坑規律，對揭示小天體表面演變機理，開展天體探測具有重要意義.

撞擊坑成坑規律研究最初主要集中在高速撞擊領域，其成坑過程及機理涉及材料的熱力學相變與破碎[4]，由于數值模擬十分困難，研究以試驗居多.Schmidt[5]基于爆炸與高速撞擊在成坑過程中的相似性，將爆炸成坑規律與結論推廣應用至高速撞擊成坑，提出撞擊成坑相似理論.Holsapple等[6-8]在常重力和超重力(500g)條件下開展球體高速（2 km/s）撞擊干砂靶成坑試驗，驗證了撞擊成坑相似理論在高速撞擊情況下的適用性.之后，不少學者開展低速（100～102m/s）撞擊驗證試驗.Yamamoto 等[9]對不同撞擊速度(11～329 m/s)下球體撞擊玻璃珠成坑瞬時過程及成坑尺寸進行試驗研究，驗證了低速撞擊條件下Schmidt 等[8]提出的相似律的適用性.Tsujido 等[10]研究了撞擊速度約為200 m/s 的彈體密度對成坑尺寸的影響.De Vet 等[11]進行速度為0.6～4.4 m/s 的撞擊試驗，驗證了成坑尺寸的撞擊能量依賴性.Takizawa 等[12]在砂土斜坡上進行速度為1～97 m/s 撞擊試驗，提出綜合考慮靶體傾角與撞擊角度的相似律關系，并驗證了該相似關系的適用性.

關于球體低速斜撞擊水平顆粒材料成坑效應的研究較少，對成坑效應的分析多集中在成坑深度和成坑直徑，對成坑體積和撞擊角度的分析相對匱乏.本研究通過系統開展不同撞擊角度下球體低速斜撞擊干砂靶成坑試驗，進一步修正低速斜撞擊水平靶體條件下考慮撞擊角度的成坑相似律，探討該相似律的適用性及其在天文學上的應用.

1 試驗方案

為了研究低速斜撞擊條件下的成坑機理及規律，設計利用重力的球體發射裝置，系統開展不同角度條件下球體撞擊干砂靶成坑試驗，并利用手持式三維激光掃描儀定量測量坑型幾何參數.

1.1 試驗裝置

如圖1 所示為可控制撞擊角度的試驗裝置.試驗裝置由發射系統、砂靶系統和測量系統組成，各裝置材料的具體規格參數如表1 所示.發射系統由球體、PVC 管、滌綸纖維、固定支架組成.PVC 管固定于固定支架上，固定支架可自由調節以控制撞擊角度，滌綸纖維置于PVC 管內部，在PVC 管底部0～3 cm 范圍進行特征標記.控制PVC管位于砂靶中心上方約1 cm，通過高速相機后續觀測可知，PVC 管對成坑過程中砂土濺射物分布幾乎無影響.砂靶由長方體開口容器、福建標準砂組成，撞擊點控制在容器中間區域，容器尺寸大于球體直徑的5 倍，以忽略在撞擊過程中容器壁對試驗結果的影響[14].測量系統由角度儀、手持式三維激光掃描儀、高速相機組成，角度儀控制PVC 管固定角度，手持式三維激光掃描儀測量坑型幾何參數，高速相機記錄撞擊過程及速度，撞擊速度過程記錄如圖2 所示.時刻t0，球體中心距PVC 管口3 cm；時刻t1，球體中心到達PVC 管口底部；時刻t2，球體底部與砂靶平面接觸.計算球體速度時，通過高速相機觀測可知，球體幾乎無轉動.近似認為在時間段t0～t1，球體做勻加速直線運動；在時間段t1～t2，球體做自由落體運動.

表1 球體發射低速撞擊試驗裝置的材料及規格參數Tab.1 Material and specification parameters of low-speed impact test device for sphere launch

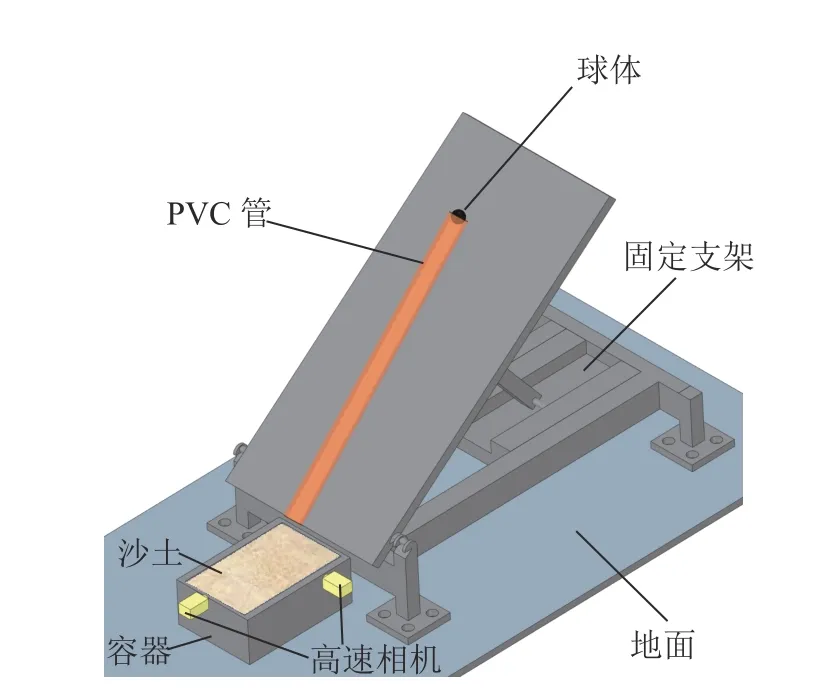
圖1 球體發射低速撞擊試驗裝置示意圖Fig.1 Schematic illustration of low-speed impact test device for sphere launch

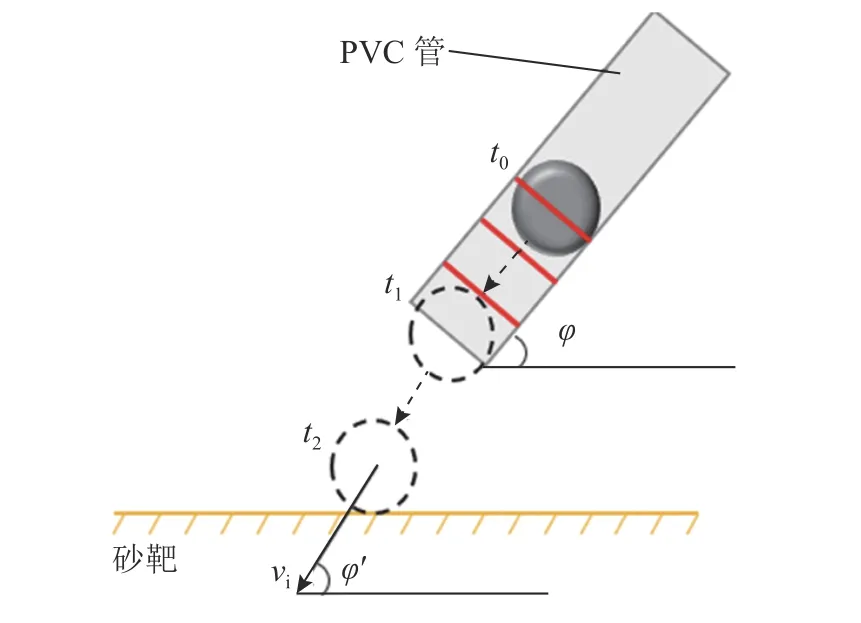
圖2 撞擊速度計算過程示意圖Fig.2 Schematic illustration of impact speed calculation process

1.2 試驗方案及工況

每次試驗開始前，取39.07 kg 砂土置于容器內，輕輕振動容器并將砂靶表面整平，控制砂土密實度為0.73.隨后利用角度儀調整PVC 管至控制角度并固定于固定支架上，將滌綸纖維穿入管內，將球體沿通孔方向穿入滌綸纖維，限制球體沿速度方向的角速度，并從PVC 管頂部釋放，撞擊砂靶成坑，全過程由高速相機記錄.試驗結束后，使用手持式三維激光掃描儀掃描，得到坑型三維點云模型.如表2 所示為設計試驗工況，共開展127 組試驗，獲得有效試驗數據107 組.表中，φ為撞擊角度，L為PVC 管長度，n為試驗組數.

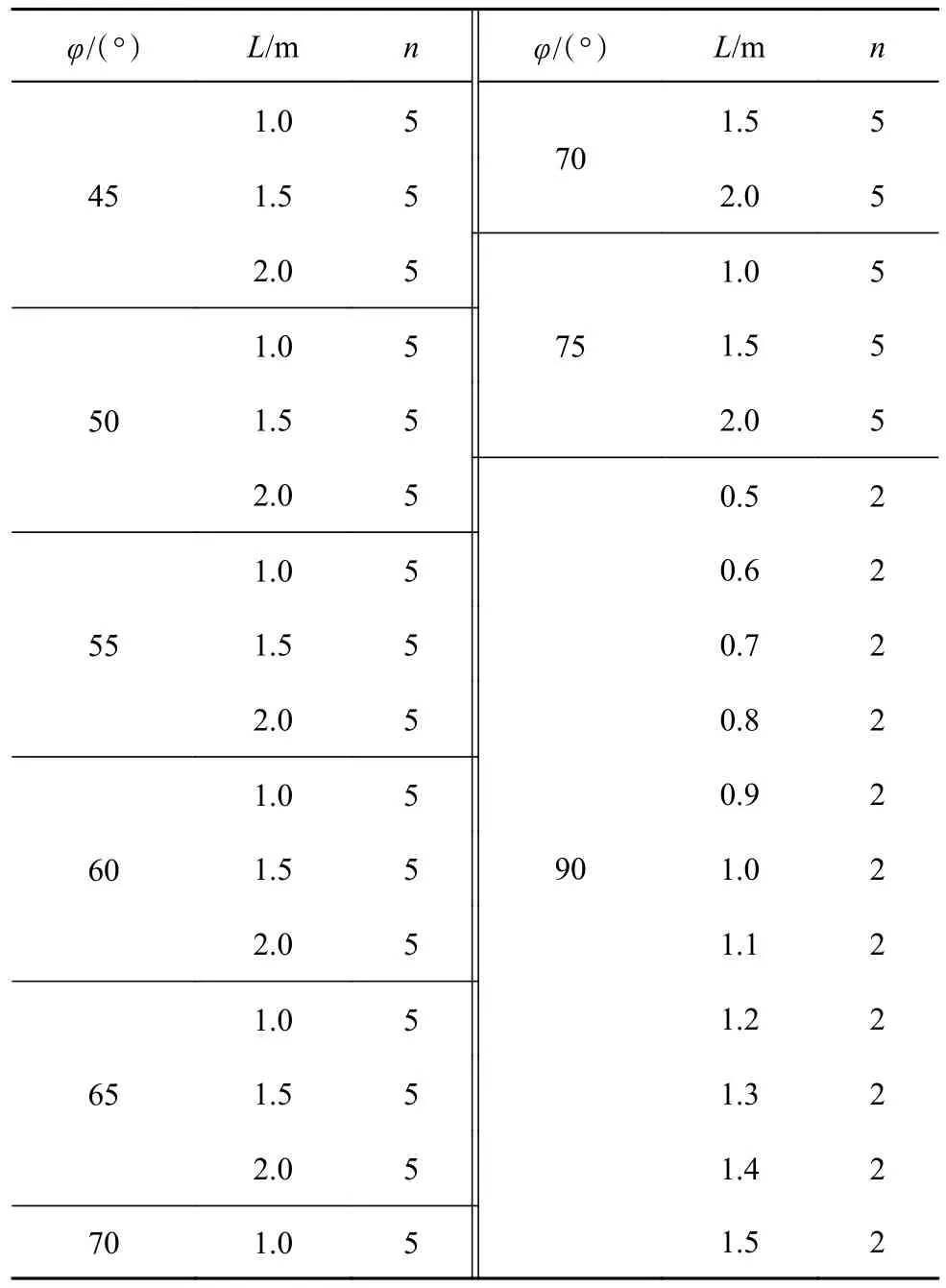
表2 球體發射低速撞擊試驗工況Tab.2 Low-speed impact experimental conditions for sphere launch

2 試驗結果

2.1 成坑過程與成坑形狀

如圖3 所示為不同撞擊角φ撞擊水平砂靶表面側視圖像，其中，時間位于圖左側，以撞擊時刻t2=0 ms，20 mm 為圖代表的真實尺寸.在撞擊速度基本相同條件下，隨著φ的減小，撞擊濺射物與水平面的夾角逐漸減小，分布于撞擊速度vi水平面投影方向的濺射物占比逐漸增大.如圖4 所示為上述撞擊形成的坑型顏色深度圖，虛線代表坑型與水平砂靶表面的截面圖，在vi基本相同的情況下，隨著φ的減小，沿速度投影方向開坑直徑增加，成坑形狀扁率增加.如圖5 所示為φ=45°，vi=3.85 m/s 條件下的等高線圖，圖中數值表示高度(初始水平面為0，豎直向上為正).坑內坡度較陡，成坑形狀近似為蛋形，濺射物分布近似為彎月形.如圖6 所示，為了定量分析成坑形狀，定義成坑參數如下.圖6（a）中，虛線代表原始地表水平面 (z=0)，坑長Dcx、坑寬Dcy分別代表成坑長軸、短軸；圖6（b）中，坑深Hc為最大坑深 Δzmax，坑體積Vc為原始地表水平面下方空腔體積.定義O-XYZ坐標系，點O為最大坑深處在砂靶平面上的投影點，XOY平面為砂靶平面，X軸正向為撞擊速度在XOY平面上的投影方向，Z軸正向指向最大坑深.

圖3 不同撞擊角度的撞擊成坑過程Fig.3 Cratering process at different impact angles

圖4 不同撞擊角度的撞擊坑型顏色深度圖Fig.4 Impact crater shapes color depth map at different impact angles

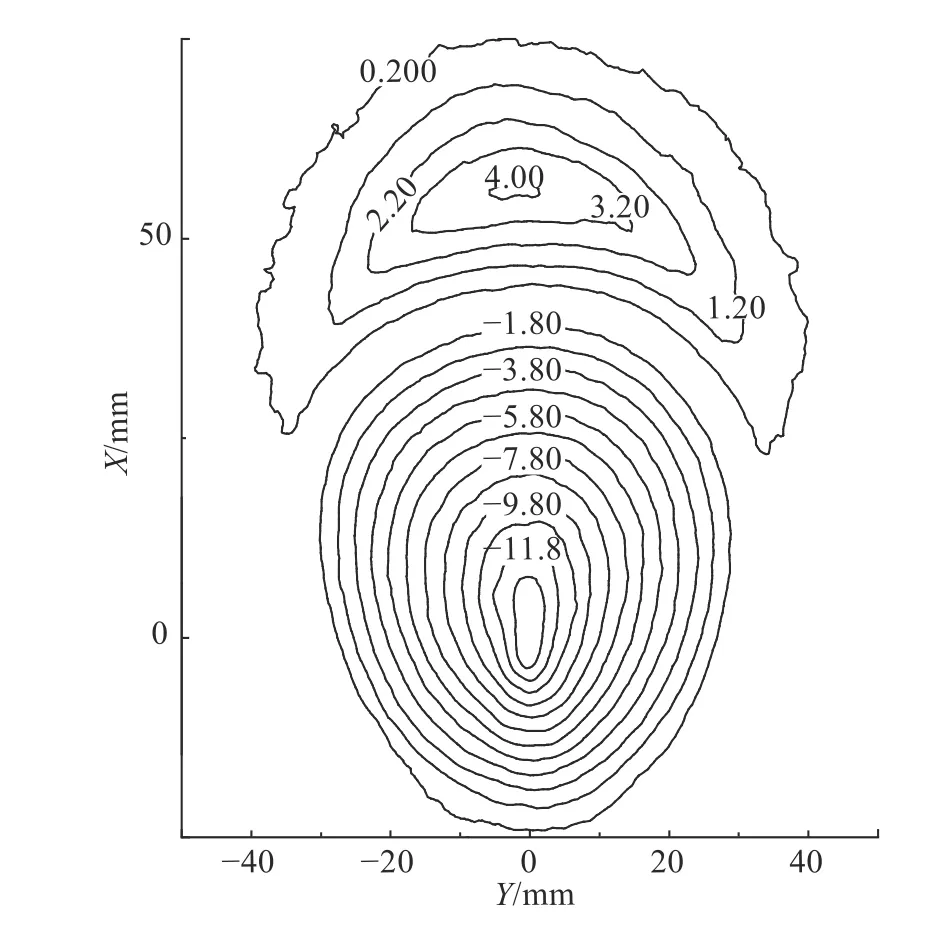
圖5 撞擊坑型等高線圖(φ=45°, vi=3.85 m/s)Fig.5 Impact crater shape contour map (φ=45°, vi=3.85 m/s)

圖6 成坑參數及坐標系定義示意圖Fig.6 Schematic illustrations of crater parameters and coordinate system definition

2.2 撞擊速度對坑型的影響

如圖7 所示為垂直撞擊下不同撞擊速度的坑型截面圖.坑長、坑深隨著撞擊速度的增加而增加，坑型左右幾乎對稱，坡度幾乎相等.當撞擊速度vi=3.22 m/s 時，坑深最低處略微突起，靶體材料的不均勻性可能是產生這種現象的主要原因.

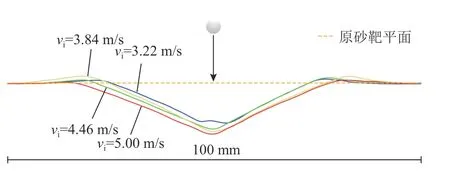
圖7 不同撞擊速度下的正撞擊YOZ 平面成坑剖面圖Fig.7 Vertical impact YOZ plane crater profile at different impact speeds

如圖8 所示為不同φ下，坑型參數隨vi的變化曲線.隨著vi的增加，Dcx、Dcy、Hc、Vc總體均呈增加趨勢，當vi≤3 m/s 或vi≥5 m/s 時，增加較緩；當vi∈(3,5)m/s時，增加較為迅速，且此趨勢隨著撞擊角度φ的增加變緩，在垂直撞擊時這種增加趨勢最小.

圖8 坑型參數隨撞擊速度的變化曲線Fig.8 Variation curve of crater parameters with impact speed

2.3 撞擊角度對坑型的影響

如圖9 所示為不同φ下的XOZ平面的成坑剖面圖.在vi基本相同情況下(vi=3.84 m/s)，隨著φ的減小，YOZ平面兩側不對稱性增強，撞擊坑沿速度投影正向被略微拉長，沿速度投影反向幾乎不變，深度方向略微減小；沿速度投影正向隆起較大，且隆起最高點隨φ的減小向遠離坑中心方向移動，沿速度投影反向隆起均較小且幾乎不隨φ變化.在φ=75°時，沿速度投影正向隆起高度出現最大值.如圖10 所示為不同φ下的YOZ平面成坑剖面圖.XOZ平面兩側幾乎對稱，在vi基本相同情況下(vi=3.84 m/s)，隨著φ的減小，Hc也隨之減小.在φ=60°時出現坡度最小.

圖9 不同撞擊角度下的XOZ 平面成坑剖面圖Fig.9 XOZ plane crater profile at different impact angles

圖10 不同撞擊角度下的YOZ 平面成坑剖面圖Fig.10 YOZ plane crater profile at different impact angles

如圖11 所示為不同vi下，坑型參數隨φ的變化曲線.在相同的vi下，隨著φ的增加，Dcx、Vc呈現出遞減趨勢；Dcy先略微增加后減小，φ≈55°附近出現最大值；Hc先減小后略微增加，φ≈75°附近出現最小值.

圖11 坑型參數隨撞擊角度的變化曲線Fig.11 Variation curve of crater parameters with impact angle

3 試驗分析

3.1 成坑過程及機理分析

基于上述試驗結果，將低速斜撞擊成坑過程分為接觸壓縮、開坑及調整3 個階段.如圖12 所示，虛線代表小球運動軌跡，深色球形代表小球所處位置.土體表面產生隆起部分用區域1 表示，濺射物回落到表面產生的堆積部分用區域2 部分表示，成坑過程中產生的濺射物部分用區域3 表示.在接觸壓縮階段，隨著球體侵徹砂坑，只存在部分因球體侵徹產生的土體擠壓隆起，此時并未產生濺射物；在開坑階段，球體完全沒入砂靶中，撞擊動能在沖擊過程中轉換為砂靶顆粒的動能，產生濺射物，土體表面出現更大隆起；在調整階段，沖擊作用結束，此時砂坑開始卸載，土體表面略微回彈，濺射物回落到表面產生堆積，最終成坑形狀由崩塌的坑壁及濺射物回落共同構成.

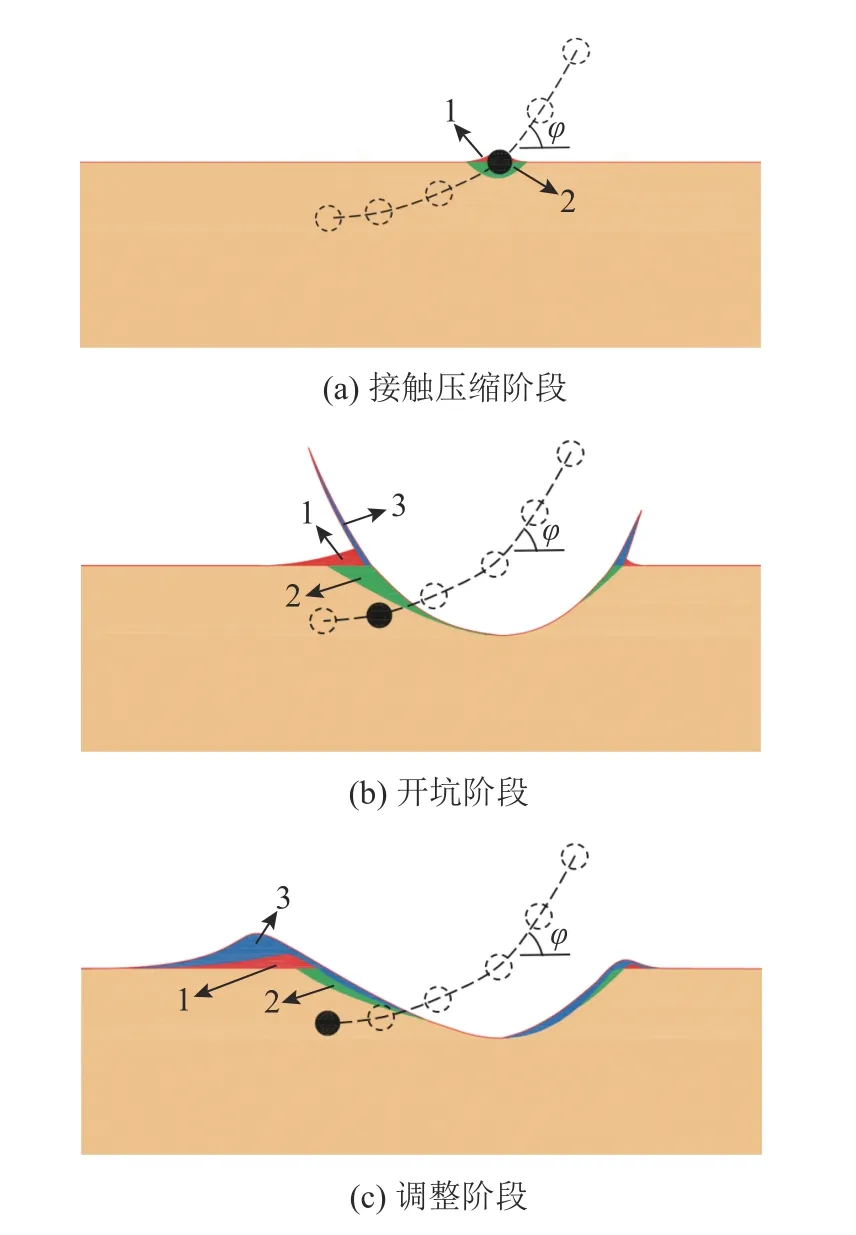
圖12 撞擊成坑過程XOZ 截面示意圖Fig.12 Schematic illustration of XOZ section of impact cratering mechanism

為了描述低速斜撞擊條件下成坑過程中顆粒流場的運動特性，采用Maxwell[15]提出的半經驗Z 模型.如圖13 所示，假設在撞擊發生后，靶體材料內瞬時形成一簇以撞擊點為中心的流線，且處于不同流線上的材料顆粒相互不存在干擾，濺射顆粒速度與撞擊點距離呈反比.在正撞擊時，顆粒流場中心發生豎向位移，顆粒流場以撞擊點為中心表現出較好的各向同性，最終產生的濺射顆粒以撞擊點為圓心均勻分布，坑型截面為圓形.在斜撞擊時，顆粒流場中心發生沿撞擊速度投影方向的位移，最終產生的濺射顆粒在速度投影方向上呈彎月形分布，在速度投影反向上濺射顆粒較少，坑型截面近似為蛋形截面.值得注意的是，Z 模型假定靶體材料的濺射角與其初始位置無關，這與試驗過程中高速相機的實際觀測到的現象存在些許差異.但基于最終坑型的觀測結果，Z 模型能夠在一定程度上說明低速正撞擊及斜撞擊條件下成坑過程中顆粒流場的運動特性.

圖13 半經驗Z 模型中靶體顆粒運動規律示意圖Fig.13 Schematic diagram of target particle movement in semiempirical Z model

3.2 成坑長徑比尺度分析

為了解撞擊角度φ對成坑形狀的影響，分析研究成坑形狀的長寬比 λ1=Dcx/Dcy、深寬比λ2=Hc/Dcy與φ的關系，當撞擊動能變化相對較小時，假設這種關系與撞擊尺度無關，即撞擊坑的形態與能量E無關[16]，λ1、λ2僅取決于φ.如圖14所示為 λ1、λ2隨φ的變化曲線.其中，λ1、λ2為試驗數據均值，上下誤差代表試驗數據極值.當45°≤φ＜60°時，隨著φ的增加，λ1、λ2迅速降低；當 60°≤φ≤90°時，λ1趨于穩定，λ2略微增加，這一趨勢與已有研究在定性上一致[17-18].

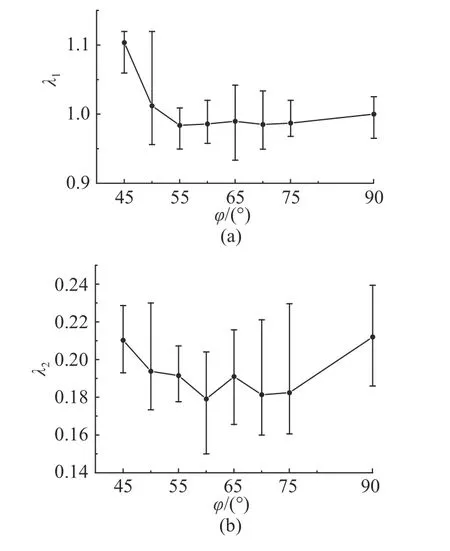
圖14 坑形長度比和深寬比隨撞擊角度的變化曲線Fig.14 Variation curve of length-to-width and depth-to-width ratios of cratering shapes with impact angle

3.3 成坑尺寸的能量依賴性

分析撞擊動能與成坑參數的關系，為了解成坑過程及機理，受初始試驗條件控制，近似認為彈丸角度為0，因此彈丸撞擊動能為

如圖15 所示為在不同φ下Dcx、Vc與E的關系，基于最小二乘法對指數函數X=aEk(X=Dcx、Vc)進行擬合，其中虛線代表擬合曲線，文中擬合方法均與此相同，k為E的冪指數，數值如表3 所示.已有研究提供了在垂直撞擊條件下的成坑直徑與E的關系，Walsh 等[19]進行的鋼球自由落體正撞擊小玻璃珠試驗得到k≈0.25；Nefzaoui 等[20]進行的水滴自由落體撞擊小玻璃珠試驗得到k≈0.18，與本研究的試驗結果基本一致.Vc與E的k≈0.48，Takizawa 等[12]進行的塑料彈丸撞擊砂土斜坡試驗得到Dcx與E的k≈0.19，Vc與E的k≈0.54.由此可見，成坑尺寸隨撞擊能量的增加而增加.

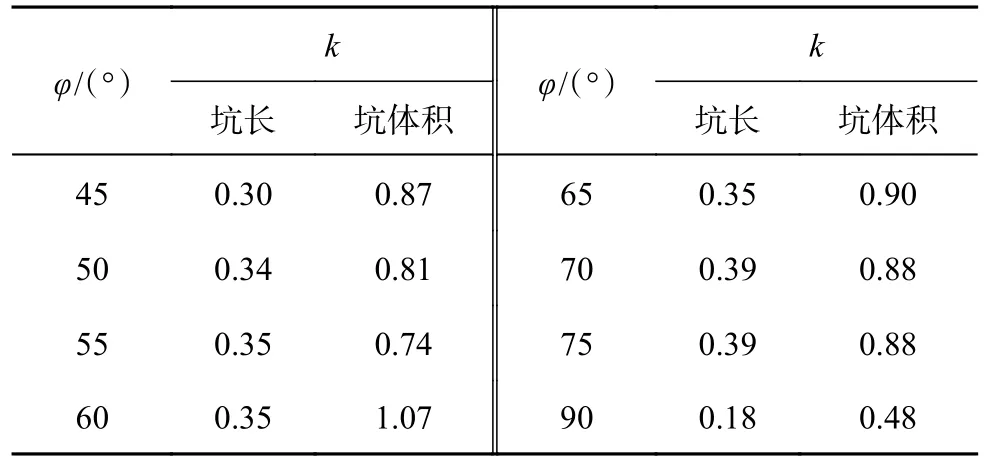
表3 撞擊動能與坑型參數的指數值Tab.3 Exponential quantity of impact energy and crater parameters

圖15 撞擊動能與成坑尺寸的關系Fig.15 Relationship between impact energy and crater size

3.4 相似律分析

為了進一步了解成坑過程以及考慮將試驗室結果應用于天文學上的可能性，基于 Π 定理進行分析，假定不考慮靶內物質沖擊變質、熔化和氣化等一系列的化學反應變化，僅在純力學情況下，成坑體積可以通過以下2 個無量綱參數得到[7]：

式中：ρt為砂靶表面密度.在本試驗中，砂靶的有效強度可以忽略不計，由重力作用主導成坑過程.當φ=90°時，π2、πV的對應關系可以很好地運用到不同尺度的撞擊過程中[8].由圖16(a)可知，π2與 πV之間存在明顯的負相關關系，但這種負相關關系的離散性較大，而且撞擊角度在無量綱參數中不被考慮.為了得到統一相似律關系，考慮對無量綱數進行修正，Takizawa 等[12]與Chapman等[21]分別考慮了撞擊動量與能量的水平分量對成坑的貢獻，提出如下修正：

圖16 成坑體積的相似律關系Fig.16 Scaling law relation of crater volume

圖16(b）、(c) 分別為 π2′、π2′′與 πV的關系，但這2 種關系仍具有較大的離散性，這可能是由于Takizawa 等[12]主要側重于考慮斜坡角度的影響.考慮到撞擊角度主要影響成坑形狀，本研究對πV提出如下修正：

式中：sinaφ為斜撞擊導致成坑形狀發生改變的系數，通過擬合確定a=1.47.圖16（d）為 π2、πV′的關系，這種關系的離散性有較好的收斂.擬合得到如下關系：

在早期相似律的研究中，部分學者使用動量描述彈丸的撞擊，部分學者采用動能描述彈丸撞擊，所獲得的相似律形式不一致.為了獲得形式統一的相似律形式，Housen 等[22]引入耦合參數，實現對動量與能量的綜合考量.定義耦合參數

式中：μ、υ 為特征指數；對于本試驗中的球形彈丸，υ=1/3 ；一般來說，1/3 ≤μ≤2/3.Ci的物理意義由指數 μ 確定.當 μ=1/3 時，Ci代表沖擊動量；當 μ=2/3 時，Ci代表沖擊動能.μ 與 π2的冪指數相關，具體為 0.59=3μ/(2+μ).得到 μ=0.49.一般來說，μ 取決于靶材料孔隙率和內摩擦的自身特性[23-24].干砂靶和無孔砂靶的 μ 分別為0.41 和0.55[17].當 μ=0.49 時，表明低速斜撞擊成坑過程中動量和能量共同影響耗散沖擊過程.

3.5 修正成坑相似理論適用性及其應用

式（9）形式與高速撞擊(vi的數量級為103m/s)、中低速撞擊(vi的數量級為101m/s)干砂靶得到的相似關系類似.如圖17 所示為在不同試驗條件下的試驗數據與式(8)的關系，本研究給出的相似律關系與以往試驗數據吻合較好，因此有理由認為考慮撞擊角度的修正相似律在不同撞擊速度下適用，尤其是水平面上的斜撞擊過程.

圖17 相似律關系在不同試驗中的適用性
Fig.17 Scaling law relation applicability for different experiments

基于上述分析，可以通過水平靶體表面撞擊坑的探測數據估計撞擊發生的初始條件，如彈體直徑、撞擊角度、撞擊速度等.例如，在執行天體探測任務時，測量水平表面上發現的撞擊坑相關尺寸，獲得參量如坑長、坑體積，撞擊角度與長寬比、深寬比之間的關系，估算得到撞擊角度；基于遙感數據以及對靶體材料的分析，估算得到天體表面重力水平以及靶體密度，此時剩下撞擊體質量、撞擊體直徑以及撞擊速度3 個未知參量.假定撞擊體為球體，且撞擊體密度與天體表面顆粒相同，基于Takizawa 等[12]的成坑寬度計算方法和式（8）的修正相似關系，計算獲得彈體質量、彈體直徑以及撞擊速度.撞擊引起的地震動會導致撞擊坑變形，從而影響撞擊坑形狀[18]，本研究修正的相似律關系僅適用于剛形成的撞擊坑.此外，角度對縱橫比、深寬比的影響很可能取決于撞擊坑的規模[25].

4 結語

為了了解撞擊坑的形成過程及規律，本研究針對水平砂靶表面進行球體低速斜撞擊試驗，得到如下結論.1）基于φ=45°～90°、vi=2.2～5.3 m/s 下球體撞擊水平顆粒表面成坑試驗，將撞擊成坑分為接觸壓縮、開坑以及調整3 個階段，分析低速斜撞擊成坑過程及機理.結果表明，成坑尺寸隨撞擊速度增加而增加；Dcx、Vc隨撞擊角度的增加而增加，Dcy隨撞擊角度的增加先減小再增加，在φ=55°附近取得極大值，Hc隨撞擊角度的增加先增加后減小，在φ≈75°附近取得極小值.2）基于Π定理，進一步修正低速斜撞擊水平靶體條件下考慮撞擊角度的成坑相似律，該相似律關系與前人試驗數據吻合較好，基本適用于水平靶體上的斜撞擊成坑過程.分析表明，低速斜撞擊成坑過程中動量和能量共同影響耗散沖擊過程.本研究僅使用1 種彈靶材料進行球體斜撞擊試驗，獲得的相似律普適性存在一定的限制，后續將開展不同彈靶材料的斜撞擊試驗以完善相似理論.