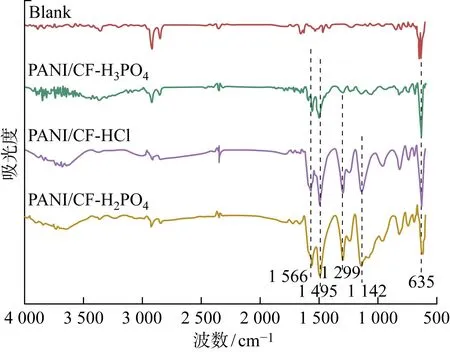
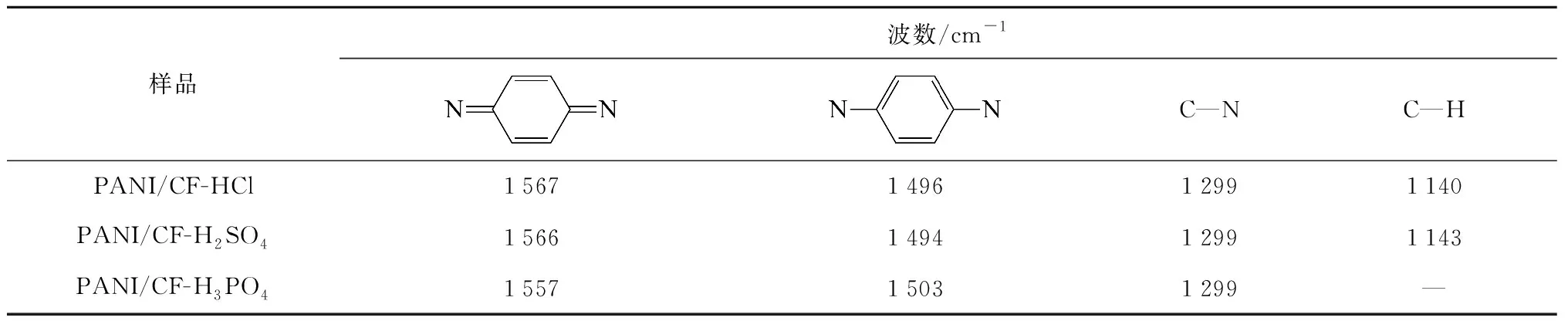
纖維增強復合材料層壓板的疲勞壽命預測方法

2024-03-28 14:40:08徐蓉霞高建雄朱鵬年吳志峯

上海交通大學學報 2024年3期

徐蓉霞, 高建雄, 朱鵬年, 吳志峯

(新疆大學機械工程學院,烏魯木齊 830017)

纖維增強復合材料(Fiber Reinforced Polymer, FRP)具有比強度高、比剛度大、壽命長、結構可設計[1-3]等諸多優點,因此其在近幾十年來應用較為廣泛[4]. 在工程實際應用中,導致其結構破壞的重要原因包括疲勞損傷造成的斷裂,但FRP有多種形式的損傷,且疲勞破壞機理十分復雜[5-6]. 在疲勞過程中,各種形式的損傷互相影響,不斷累積,FRP的機械性能也隨之發生退化[7]. FRP的疲勞壽命模型一般是根據應力-壽命曲線(S-N曲線)或Goodman疲勞壽命曲線來預測特定載荷下的疲勞壽命. 這種方法不考慮疲勞損傷的微觀機理、材料的性能退化、損傷之間的耦合和損傷的累積,而且往往需要大量的實驗數據來建立疲勞壽命曲線. 或者通過漸進疲勞損傷分析模型來預測其疲勞壽命,該方法涵蓋疲勞加載過程中應力分析、疲勞失效準則和材料性能退化模型3部分. 因此,FRP層壓板的疲勞壽命,可以基于經典層壓板理論分析單層板的應力來預測,但該計算過程繁瑣,且認為同一單層板的受力均勻,因此預測誤差較大. 基于以上問題,本文提出了單向板的載荷水平-疲勞壽命曲線(q-N曲線),與層壓板的有限元分析緊密結合來預測FRP層壓板的疲勞壽命方法.

目前用于表征復合材料疲勞損傷擴展的參量有疲勞模量、剩余強度、應變等物理量,基于這些物理量,可以構造出多種疲勞損傷和疲勞壽命模型[8-9]. 本文用疲勞模量來描述碳纖維增強復合材料的損傷演化規律,從而建立疲勞壽命的函數表達式. 以單向板在單軸循環應力加載下載荷比與疲勞壽命的試驗數據為基礎,利用灰色系統等間距GM(1, 1)模型[10],構造單向板的疲勞壽命和損傷函數模型.

復合材料的疲勞過程從本質上講是損傷不斷累積,材料性質不斷退化,應力重新分布的動態過程[11-12]. 本文將FRP層壓板的疲勞失效過程簡化為:在應力加載下,單層板的危險單元失效,導致該單層的材料性質發生改變,從而對該層材料進行剛度退化,隨之應力分布改變的循環過程. 利用Abaqus對層壓板建模分析,獲取每單層的應力分布,進而提取危險點的應力,通過Hashin損傷失效準則[13],判斷該層的失效模式,然后對失效單層進行剛度退化,循環該過程,確定單層的失效強度以及層壓板的拉伸強度. 通過該有限元分析過程中所得的應力分布,與灰色系統建立的單向板的疲勞壽命計算公式結合,以此來預測FRP層壓板的疲勞壽命. 通過與實驗數據以及其他文獻方法的預測結果對比,來驗證該方法的有效性.

1 基于灰色系統GM(1, 1)模型建立單向板的q-N函數

灰色系統理論是一種研究“小樣本”“貧信息”不確定性問題的方法,主要提取“部分”已知信息,實現對系統演化規律的正確描述[14]. 灰色預測建模方法種類繁多,其中等間距GM(1, 1)模型具有樣本需求小、建模過程簡單等優點. 當建立單向板的疲勞壽命預測模型時,在實驗數據較少的情況下,若用最小二乘法擬合函數曲線,將導致誤差較大. 因此,借助灰色系統建立單向板的疲勞壽命函數,首先引入疲勞模量衰減的雙參數模型.

1.1 疲勞模量的概念

Hwang等[15]首先引入疲勞模量的概念,提出通過疲勞模量來預測疲勞壽命. 文獻[16]中以碳纖維為研究對象,給出了循環應力最大值與應力循環次數n有關的疲勞模量的定義:

(1)

式中:σmax為外加循環應力的最大值;En為第n個循環時的疲勞模量;載荷比q表征應力水平,q=σmax/σu,σu為極限強度;εn為第n個循環后的累積應變,包含了第n次循環時的彈性應變.

En的初值、終值條件為

(2)

式中:E0為材料的靜態彈性模量,在工程上,假定n=0時的疲勞模量等于E0;EN為經過N個循環后,材料發生疲勞破壞時的疲勞模量,N即為疲勞壽命.因此,E0是常數,EN取決于外載荷. Hwang等[17]提出了疲勞模量衰減三參數模型以及可以簡化的雙參數模型. 其中,如下式所示的雙參數模型的疲勞壽命預測值與實驗數據吻合較好,而且簡單,因此本文選用此模型預測疲勞壽命:

(3)

式中:A、B均為材料常數.

1.2 FRP單向板的疲勞壽命分析

以單向板受縱向拉-拉循環載荷為例,來說明單軸循環應力下單向板疲勞壽命的計算方法. 定義如下物理量[18]:

(4)

式中:Xt為單向板的縱向拉伸強度;εut為縱向靜態極限應變;E11為縱向靜態彈性模量;εN表示疲勞破壞時的極限應變.將式(3)從第n1個循環到第n2個循環進行積分:

(5)

令nn=n,n1=1,式(5)可以簡化為

(6)

(7)

假設單向板在承受N次循環載荷后發生疲勞破壞,那么EN便可作為疲勞模量的臨界值.令k1=εN/εut,則N可以表示為

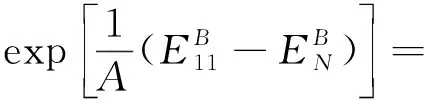
(8)

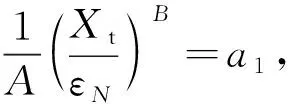
(9)

式中:a1、k1均為材料參數.當B=1時,式(9)簡化為N=exp[a1(k1-q)].

1.3 損傷函數的構成

假設復合材料無初始損傷,疲勞損傷函數的定義Dn=(εn-ε0)/(εN-ε0)應滿足下列初值、終值條件:

(10)

以單向板受縱向單軸循環應力作用為例,以應變和疲勞模量為中間量,建立損傷函數,其過程如下:

(11)

同樣的方法,可以建立單向板在其他兩個主軸方向上(橫向和面內剪切)形如式(11)所示的疲勞損傷函數. 因此三參數和雙參數疲勞損傷累積公式分別如下所示:

(12)

(13)

根據式(12)和式(13)所示的損傷累積公式,計算單向板在3個主軸方向上循環應力加載造成的損傷,分別表示為:D1、D2、D12.考慮多向應力的綜合作用效果,定義復合型損傷:

(14)

式中:D11表示多軸循環應力加載下纖維的損傷程度;D22則反映基體的損傷程度. 只要其中任何一個首先達到1,單向板就發生了疲勞失效. 但疲勞極限本身存在模糊性,因此當復合型損傷很接近1時單向板也有可能發生了疲勞失效.

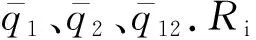
(15)

式中:Yt為橫向拉伸強度;Sin為面內剪切強度;σ1,max、σ2,max表示縱向和橫向兩個方向上的最大主應力;τ12,max為剪切方向最大應力;νij表示應力作用在i方向時,在j方向引起的橫向變形的泊松比,i,j=1, 2.將等效載荷比代入建立的q-N函數表達式中,計算對應的疲勞壽命.

1.4 灰色系統等間距GM(1, 1)建模

灰色系統模型通過序列的累加生成,揭示系統的發展趨勢,累加生成處理后的序列呈現單調遞增的規律. 設X(0)為原始序列,X(1)為一次累加生成序列,Z(1)為均值序列,表達式為X(0)=[x(0)(1)x(0)(2) …x(0)(n)],X(1)=[x(1)(1)x(1)(2) …x(1)(n)],Z(1)=[z(1)(1)z(1)(2) …z(1)(n)].

其中,累加序列當序列數k=1時,x(1)(1)=x(0)(0),當k為其他值時,如下式所示:

x(1)(k)=(x(0)(k)+x(1)(k-1))

(16)

k=2,3,…,n

均值序列為

z(1)(k)=0.5(x(1)(k)+x(1)(k-1)),

k=2,3,…,n

(17)

則x(1)上的灰微分方程為x(0)(k)+az(1)(k)=b,其白化方程為dx(1)/dt+ax(1)=b.其中,參數a和b根據下式計算:

(18)

(19)

參數C、D、E、F可以根據原始序列、一次累加序列以及均值序列得到:

(20)

(21)

(22)

(23)

白化方程式的解為x(1)(t)=(x(1)(1)-b/a)exp(-at)+b/a,其中t表示時間,則灰色系統GM(1, 1)模型的時間響應序列為x(1)(k+1)=(x(0)(1)-b/a)exp(-ak)+b/a,其中k=1,2,…,n.因此,該模型的預測結果計算式如下:

x(0)(k+1)=x(1)(k+1)-x(1)(k)=

(24)

k=1,2,…,n

設單層板在單軸循環應力作用下,不同載荷比下的疲勞壽命視為一個灰色系統中,疲勞壽命構成一個原始序列,根據灰色等間距GM(1, 1)建模,擴展實驗數據,然后擬合q-N函數曲線.

1.5 基于灰色系統建立FRP單層板在單軸循環應力作用下的q-N曲線和損傷函數

對于T300/QY8911復合材料單向板[0]16, 文獻[19]中給出了應力比R=0.1時的縱向拉-拉疲勞試驗數據,如表1所示.

表1 [0]16單向板在縱向應力作用下疲勞試驗數據

首先,用最小二乘法擬合雙參數和三參數q-N曲線的函數表達式如下所示:

q=-0.035lnN+1.189

(25)

q=(1.778×10-5lnN+2.132)-6.597

(26)

建立灰色等間距模型時,需要等間距載荷比下的疲勞壽命,根據插值法,計算q=0.75時的N=2.71×105. 因此灰色等間距GM(1, 1)模型原始序列可以設為X(0)=[2.50×1032.40×1041.43×1052.71×1054.57×105],根據式(16)～(23),計算一次累加序列和均值序列,C=1.086 5×106,D=8.95×105,E=4.027 5×1011,F=5.504×1011,a=-0.625 4,b=53 882.根據式(24)計算當q=0.65,0.6,0.55,0.5時,N=9.40×105,1.76×106,3.28×106,6.14×106.在灰色系統建模時,發現q=0.85時曲線突變,因此將該曲線分段,擬合的雙參數和三參數q-N函數,分別如下所示:

(27)

(28)

將4種方法進行誤差對比分析,結果如表2所示.

表2 擬合[0]16單向板q-N函數不同方法的精度對比Tab.2 Precision comparison of different methods for fitting q-N function of [0]16 uni-directional plates

由表2可知,最小二乘法擬合三參數q-N函數的方法誤差太大, 因此不再做函數曲線圖.其他3種方法的q-lgN函數曲線如圖1所示.

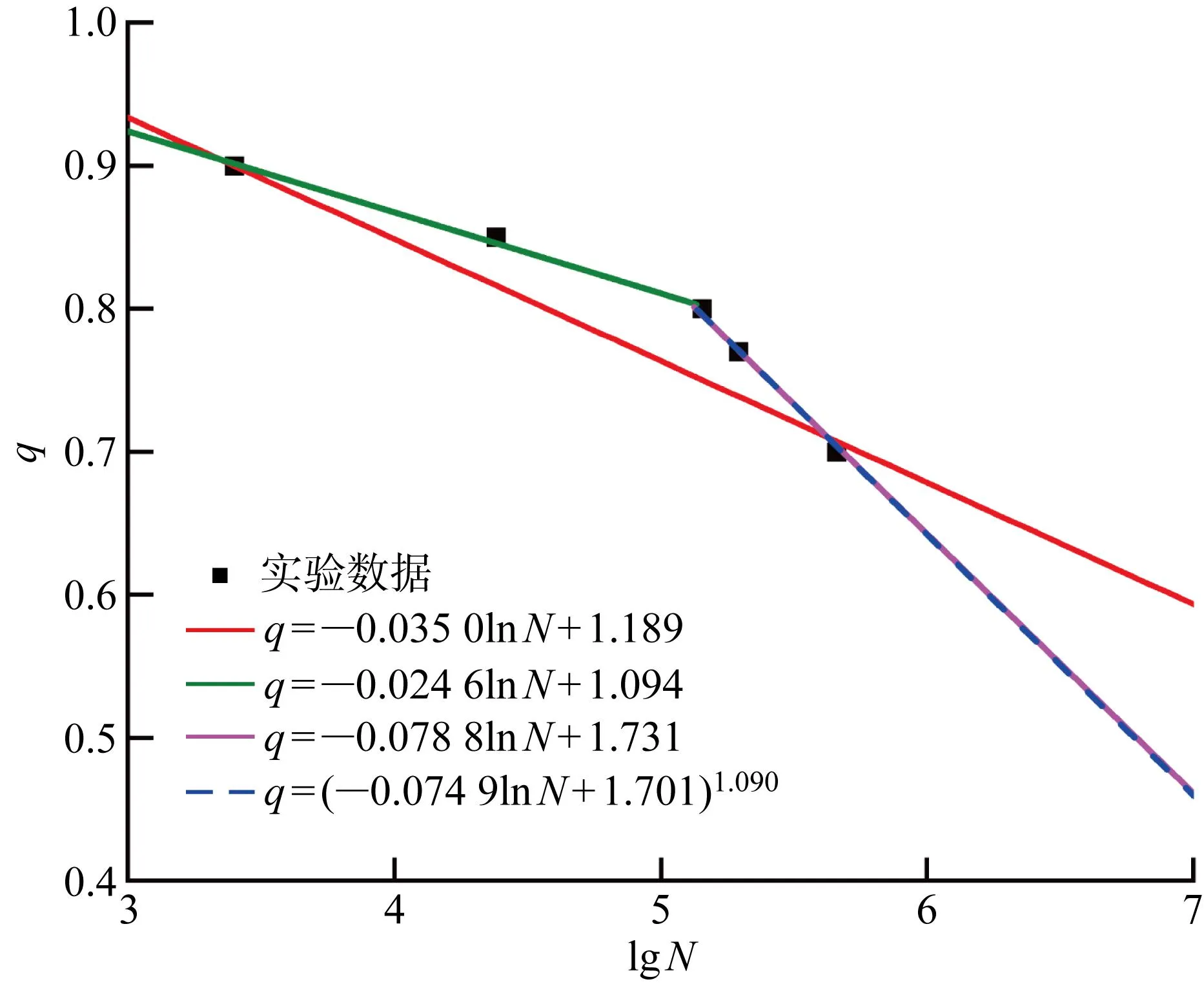
圖1 3種建模方式擬合[0]16單向板的q-lg N曲線Fig.1 Fitting of q-lg N curves of [0]16 uni-directional plates of three modeling methods

通過表2和圖1可以發現,通過灰色系統建立的q-N函數,精度明顯得到了提高. 本文在計算縱向損傷量時,選用擬合曲線與實驗數據相對誤差最小的灰色系統擬合的三參數q-N函數. 因此損傷函數為

(29)

橫向拉-拉建模數據根據[90]20單向板拉-拉疲勞實驗獲得[19],如表3所示.

表3 [90]20單向板在橫向應力作用下的疲勞實驗數據(R=0.1)

首先,用最小二乘法擬合q-N函數. 擬合雙參數q-N曲線的函數表達式如下所示:

q=-0.036 4lnN+1.128

(30)

擬合三參數q-N函數的發展趨勢不符合復合材料q-N函數發展趨勢,因此暫不考慮該方法. 根據插值法,計算出q=0.95,0.85,0.75時,N=550.5, 2.245×103, 8.124×104. 灰色等間距模型原始序列設為X(0)=[550.5 1.01×1032.245×1033.48×1038.124×1041.59×105]. 根據式(16)～(23)計算一次累加序列和均值序列,C=225 215,D=246 975,E=3.063 4×1010,F=3.056 7×1010,a=-0.955 3.根據式(24),計算當q=0.65,0.6,0.55時,N=1.369 1×106,3.559×106,9.251 4×106.將這9組數據,用最小二乘法擬合雙參數和三參數q-N函數,結果如下所示:

q=-0.034 1lnN+1.111

(31)

q=(0.27lnN-0.519)-0.391

(32)

將基于橫向拉-拉疲勞試驗數據的3種擬合方法的誤差進行對比分析,結果如表4所示.

表4 擬合[90]20單向板q-N函數不同方法的精度對比Tab.4 Precision comparison of different methods for fitting q-N function of [90]20 uni-directional plates

3種方法擬合的q-lgN函數曲線,如圖2所示.

灰色系統擬合的q-N三參數方法的誤差最小,根據損傷函數,計算3個參數時發現,參數k不是實數,不能計算本文運用的損傷函數. 因此,選用灰色系統擬合的雙參數q-N函數. 所以損傷函數為

(33)

面內剪切疲勞實驗數據,根據[0/90]4s剪-剪疲勞實驗獲得[19],如表5所示.

根據這5組數據,用最小二乘法擬合雙參數和三參數q-N函數,結果如下所示:

圖2 3種建模方式擬合[90]20單向板的q-lg N曲線Fig.2 Fitting of [90]20 uni-directional plates q-lg N of three modeling methods

表5 [0/90]4s層壓板在面內剪切應力作用下的疲勞實驗數據(R=0.1)

q=-0.051 1lnN+1.117

(34)

q=(-0.042 0lnN+1.108)1.354

(35)

根據插值法,計算q=0.75,0.65,0.55時,N=1 874, 14 075, 101 400. 設原始序列為X(0)=[2293981 8743.35×1031.407 5×1042.48×1041.014×1051.59×105]. 根據式(16)～(23),計算一次累加序列和均值序列,C=381 930,D=323 897,E=5.252 9×1010,F=6.562 2×1010,a=-0.778 3.根據式(24)計算q=0.45,0.4,0.35時,N=1.399 7×106,3.048 4×106,6.638 8×106.基于這9組數據,用最小二乘法擬合雙參數和三參數q-N函數,結果如下所示:

q=-0.046 2lnN+1.081

(36)

q=(-0.030 8lnN+1.082)1.956 9

(37)

將4種方法進行誤差對比分析,結果如表6所示.

4種方法擬合q-lgN函數曲線,擬合結果如圖3所示.

通過表6和圖3可以發現,雙參數q-N曲線的誤差較小. 因此,本文在計算剪切損傷量時,選用雙參數q-N曲線. 所以損傷函數為

(38)

圖3 4種建模方式擬合[0/90]4s層壓板q-lg N曲線Fig.3 Fitting of q-lg N curves of the [0/90]4s laminate of four modeling methods

表6 擬合[0/90]4 s層壓板q-N函數不同方法的精度對比Tab.6 Precision comparison of different methods for fitting [0/90]4 s laminate q-N function

2 FRP多向層壓板的疲勞壽命

本文FRP層壓板疲勞壽命預測的步驟為兩大部分,第1部分是通過應力分析和失效分析,計算該層壓板的拉伸強度. 第2部分是基于FRP層壓板的拉伸強度和典型FRP單向板的疲勞壽命預測函數以及損傷函數來計算層壓板的疲勞壽命. 對FRP層壓板的疲勞壽命預測過程作如下假設:

(1) 多向層壓板中的各單向板具有相同的疲勞性能,且層壓板沒有初始損傷[18].

(2) 把層壓板的疲勞失效看成是不同單層逐次發生失效的間斷過程,把材料性質的連續退化過程簡化為單層的危險部位失效后,材料性質退化,應力分布改變.

2.1 FRP多向層壓板的應力分析和失效分析

假設FRP層壓板處于平面應力狀態,利用Abaqus建模對層壓板進行應力分析. 具體步驟如下.

(1) 通過Abaqus仿真拉伸實驗,在加載外力P時,設定循環周期增量P,僅對Δn、Δ2n、Δ3n循環周期下的層壓板進行應力分析和單元失效判斷. 在Δn內只進行材料性能漸降,忽略性能突降. 選擇合適的面內強度準則,判斷是否失效. 本文選用Tsai-Hill強度準則[20]判定:

(39)

式中:σ11、σ22、τ12分別表示縱向、橫向及剪切方向的應力.

(2) 計算單向板的失效強度.首先計算各單層的強度比RL,

(40)

找出最小強度比RLmin,強度比最小的單層為最先失效層. 然后計算該層的失效強度FS,

FS=PRLmin

(41)

根據Hashin失效準則,判斷失效模式:

(42)

(43)

式中:S12為xy面內切應力.

若滿足式(42)則為纖維拉伸失效,若滿足式(43)則為基體拉伸失效. 若根據式(40)判斷出該層已失效,判斷失效模式時,兩個都未達到失效,則根據相對大小判斷失效模式,造成這種現象的原因是本文沒考慮層間應力的影響.

(3) 對失效的單層進行剛度退化.本文采用Tsai提出的0.4Em剛度退化準則[21]:纖維斷裂后,該層便不起作用了,其正軸模量矩陣Q退化為零矩陣,即Q11=Q22=Q12=Q66=0;基體的破壞退化規則為:縱向拉伸模量E11,泊松比ν12保持不變,橫向拉伸模量E22下降至0.56E22,面內切變模量G12下降至0.

(4) 重復該過程,直到層壓板失效,以單向板的失效強度最大值作為層壓板的拉伸強度.

應力分析和失效分析的具體過程如圖4所示.

2.2 FRP多向層壓板的疲勞壽命

(1) 根據第1部分的結果得知層壓板的極限拉伸強度SE,確定循環載荷的最大外載荷Pb:

Pb=SEq

(44)

(2) 復合材料層壓板在載荷加載時,失效層的破壞可能是靜強度破壞或者疲勞破壞. 如果Pb>FS,屬于靜力破壞,發生靜力破壞的單層也消耗了一定數量的疲勞壽命,計算等效的疲勞累積損傷. 如果發生纖維斷裂,則將該層的累積損傷量D1、D2、D12均置為1,如果發生基體破壞, 將面內橫向應力引起的累積損傷量D2置為1[18]. 若Pb

(4) 分別根據q-N函數表達式(28)、(31)、(36)計算其壽命n1、n2、n12,選擇三者中最小的記為nmin,再根據損傷函數式(29)、(33)、(38)以nmin為初值進行迭代.

(5) 根據式(14)計算復合損傷D11、D22,判斷D11、D22其中之一是否滿足大于0.999,滿足時迭代結束,若不滿足,進行循環迭代,具體迭代方法如圖5 所示. 迭代終值N為該單向板的疲勞壽命. 隨后對該單向板根據其失效模式,進行剛度退化,即對材料屬性進行改變. 因為材料的疲勞極限存在模糊性,累積損傷也不一定為1,所以當循環迭代時,n增加的緩慢時迭代結束,根據本文算例結果,將本文迭代終值復合損傷定義為0.999.

圖5 層壓板疲勞壽命計算Fig.5 Calculation of fatigue life of laminate

(6) 重復上述步驟,直到層壓板失效.各單向板的累積壽命和為層壓板的疲勞壽命.

3 實例驗證與對比分析

材料T300/QY8911的彈性常數[22]縱向拉伸模量E11=135 GPa,橫向拉伸模量E22=8.8 GPa,法向拉伸模量E33=8.8 GPa;泊松比ν12=0.33,ν23=0.48,ν13=0.33;Gij表示i-j面內切變模量,G12=4.47 GPa,G23=3.2 GPa,G13=4.47 GPa;強度參數[23]Xt=1 627.5 MPa,縱向壓縮強度Xc=1 226 MPa,Yt=68.4 MPa,橫向壓縮強度Yc=218 MPa,Sin=89.9 MPa.

3.1 算例1

層壓板的鋪層方式為[0/90]4s,長40 mm,寬20 mm,單層厚度為0.125 mm[23].根據材料的彈性參數和強度參數,采用Abaqus建立分析計算模型,R=0.1,q=0.85.為了提高計算精度,網格沿寬度方向從邊界向中間由密變疏,對網格劃分進行收斂性分析以及網格無關性檢查,最終確定有限元模型的網格大小是:兩端是邊長為0.5 mm的正方體,中間是邊長為1 mm的正方體. 單元所用類型為Continum shell: SC8R,單元數量為 9 600,所建有限元模型如圖6所示,鋪層方式如圖7所示.圖中:Angle=0表示該單向板鋪層角為0°,即單向板鋪層的縱向與層壓板參考坐標X軸之間的夾角為0°,Angle=90表示該單向板鋪層角為90°;Ply-1—Ply-16分別表示該層壓板的鋪層,共有16層.

圖6 [0/90]4s層壓板的模型Fig.6 Model of [0/90]4s laminate

圖7 [0/90]4s的鋪層方式Fig.7 Laying method of [0/90]4s laminate

在層壓板左側端面施加完全約束,在層壓板右側端面施加均布力載荷. 然后施加載荷,當P逐漸增加到560 MPa時:90°鋪層危險點的應力分布為σ11=-6.271 MPa,σ22=68.34 MPa,τ12=4.644 MPa. 根據式(39)判斷該層是否失效:

1.001 1>1

(45)

根據式(45)結果大于1,所以90° 鋪層失效,該層的失效強度比RL(90°)=0.999 5,失效強度FS(90°)=559.72 MPa. 根據失效準則判斷該層的失效模式為基體失效. 0° 鋪層危險點的應力分布為σ11=1 096 MPa,σ22=19.93 MPa,τ12=13.93 MPa. 判斷該層是否失效:

0.554 2<1

(46)

根據式(46)結果小于1,因此0°鋪層未失效. 所以對90°鋪層根據本文選定的剛度退化準則進行剛度退化. 然后施加載荷,當載荷增加到738 MPa時:0°鋪層危險點的應力分布為σ11=1 464 MPa,σ22=29.8 MPa,τ12=12.27 MPa. 判斷該層是否失效:

1.001 1>1

(47)

由式(47)計算結果大于1,因此0°鋪層失效,該層的失效強度比RL(0°)=0.999 4,失效強度FS(0°)=737 MPa,失效模式為纖維斷裂. 極限強度SE=737 MPa,根據式(44),計算循環載荷的最大外載荷,Pb=SEq=626.5 MPa. 因為FS(90°)Pb,因此,0°鋪層因為疲勞破壞而失效.

(48)

D11>1,則該單向板的壽命為2.330 6×105. 因此,該層壓板的疲勞壽命為2.331 06×105. 根據文獻[23],該層壓板的疲勞壽命實驗數據為 2.33×105,將本文預測結果、多個文獻方法與實驗數據計算相對誤差,結果進行對比,如表7所示.

表7 不同方法預測[0/90]4s層壓板的疲勞壽命結果對比

3.2 算例2

層壓板的鋪層方式為[-60/0/60]3s,其在Abaqus建模時,材料屬性、模型尺寸、網格劃分、單元類型以及加載方式均與算例1一致,q=0.8. 施加載荷,當P逐漸增加到320 MPa時:-60° 鋪層危險點的應力分布為σ11=-160.3 MPa,σ22=64.17 MPa,τ12=29.98 MPa. 判斷該層是否失效:

1.004 9>1

(49)

根據式(49)的計算結果大于1,因此-60°鋪層失效,失效強度比RL(-60°)=0.997 5,失效強度FS(-60°)=319.2 MPa,失效模式是基體破壞. 60°鋪層危險點的應力分布為σ11=-160.9 MPa,σ22=64.14 MPa,τ12=29.92 MPa. 判斷該層是否失效:

1.003 8>1

(50)

根據式(50)的計算結果大于1,因此60°鋪層失效,失效強度比RL(60°)=0.998 1,失效強度FS(60°)=319.4 MPa,失效模式是基體破壞. 0°鋪層危險點的應力分布為σ11=1 235 MPa,σ22=8.705 MPa,τ12=20.93 MPa. 判斷該層是否失效:

0.642 2<1

(51)

根據式(51)的計算結果小于1,因此0° 鋪層未失效. 對 -60° 和60° 鋪層,根據本文選定的剛度退化準則進行剛度退化,然后施加載荷,當載荷增加到350 MPa時:0° 鋪層危險點的應力分布為σ11=1 558 MPa,σ22=10.06 MPa,τ12=26.25 MPa. 判斷該層是否失效:

1.017 4>1

(52)

表8 不同方法預測[-60/0/60]3s層壓板的疲勞壽命結果對比

4 結論

復合材料層壓板內部損傷會引起剛度退化,而損傷不斷累積會導致其疲勞破壞. 以疲勞模量為參量,借助灰色系統構造FRP單向板的損傷函數和疲勞壽命函數,通過建模對FRP層壓板有限元分析,對其疲勞破壞過程模擬. 這種理論與仿真結合預測FRP多向層壓板疲勞壽命的方法可以得到以下結論:

(1) 通過灰色系統GM(1, 1)模型建模,擬合了q-N函數表達式以及損傷函數表達式,且擬合結果與最小二乘法擬合的結果相比提高了預測精度,擬合的疲勞壽命和損傷函數可直接用于同種材料任意鋪層的多向層壓板的壽命預測.

(2) 基于Abaqus模擬仿真,對多層板進行應力分析和失效分析,然后與建立的q-N函數結合,以此來預測FRP多層板的疲勞壽命. 該方法與傳統的經典層壓板理論做應力分析的方法相比減小了誤差. 因為經典層壓板理論認為,單層板的應力分布是均勻的,但事實上,受力點與受力方向都會使單層板存在危險點,而通過Abaqus建模,可以解決這個問題.

(3) 本文理論與模擬仿真緊密結合的方法突破了以往完全依賴試件疲勞試驗或者只有仿真的預測方法. 通過算例驗證,證明了該方法的有效性,具有一定的工程應用價值.

附錄