指數有界雙連續n階α次積分C半群的擾動
趙華新, 賀凱麗, 劉娟娟
(延安大學 數學與計算機科學學院, 陜西 延安 716000)
算子半群理論在泛函分析和實際問題中有著廣泛的應用,經過多年的持續發展,算子半群種類不斷豐實,算子半群的擾動是算子半群理論研究的重要內容,許多學者對此作了大量研究工作。文獻[1-2]討論了n次積分C半群的擾動;文獻[3-4]討論了α次積分C半群的擾動;文獻[5-6]討論了雙參數C半群的指數公式、譜及其擾動;文獻[7-8]討論了擾動雙參數C半群的相關性質;文獻[9]研究了指數有界雙連續α次積分C半群的擾動;文獻[10-11]給出了雙連續n次積分C半群的定義及其性質;文獻[12-14]討論了n階α次積分C半群擾動、指數有界性和緊性;文獻[15]研究了指數有界雙連續n階α次積分C半群的定義及其性質;文獻[16]討論了指數有界雙連續n階α次積分C半群的生成定理。對于指數有界雙連續n階α次積分C半群的擾動還尚未被研究。本文在此理論基礎上,給出指數有界雙連續n階α次積分C半群的擾動的結果并進行證明,從而進一步完善了雙連續n階α次積分C半群的相關理論。
1 預備知識
文中假設X為無限維的復Banach空間,B(X)是X上的有界線性算子全體所組成的代數;D(A)為線性算子A的定義域,X′是X的共軛空間,τ是X上的一個局部凸拓撲并具有以下性質:


設T(t)∈B(X),n∈N,α≥0,
T(t)=0當且僅當存在n≥0使JnT(t)=0,t≥0。
2 基本概念和引理


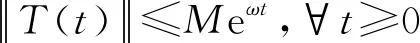
定義4[10]設C∈B(X)為單射,n∈N,α≥0,若:
2) 存在閉線性算子A,滿足
3) {T(t)}t≥0強τ連續,即對每個x∈X,映射t→T(t)xτ連續;
4) {T(t)}t≥0等度雙連續;
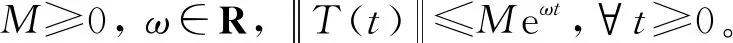
則算子族{T(t)}t≥0?B(X)稱為指數有界雙連續n階α次積分C半群。其中A為其次生成元,把Gτ(M,ω,C)記為X內的所有指數有界雙連續n階α次積分C半群。……

