對一道解析幾何模考題的探究

鐘國城

(廣東省梅縣東山中學,廣東 梅州 514017)

解析幾何是高考的熱點與難點內容,解析幾何解答題通常處于壓軸題的位置,難度較大,學生在求解時難于求解出答案.本文將通過一道解析幾何模考題的多角度探究,幫助學生突破解析幾何障礙,提升解題能力.

1 題目呈現

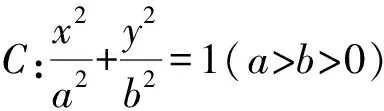
(1)求C的方程;

(2)直線l:y=k(x-1)(k≠0)與C相交于A,B兩點,過C上的點P作x軸的平行線交線段AB于點Q,直線OP的斜率為k′(O為坐標原點),△APQ的面積為S1,△BPQ的面積為S2.若|AP|·S2=|BP|·S1,判斷k·k′是否為定值?并說明理由.

2 總體分析

本題第(1)問考查橢圓的標準方程,根據題意建立有關a,b,c的方程組,求解方程組即可得到答案,屬于常規問題;第(2)問利用直線與橢圓的位置關系研究有關斜率的定值問題,此問可以多視角解答,涉及三角形面積、角平分線定理、弦長公式等知識,重點考查化歸與轉化、方程等數學思想,全面考查學生的數學運算、邏輯推理等數學核心素養.本文將對第(2)問進行多角度探究,以饗讀者.

3 試題解答

以下重點探討第(2)問,解決此問的關鍵在于條件|AP|·S2=|BP|·S1的轉化,可以從四個方面入手.

解法1 設P(x0,y0),A(x1,y1),B(x2,y2),直線AP與BP的斜率分別為k1與k2(k1≠k2),則

因為|AP|·S2=|BP|·S1,

所以|AP|·|y2-y0|=|BP|·|y1-y0|.

即k1+k2=0.

評注此法利用弦長公式與面積公式將條件坐標化,進而轉化出斜率之間的關系,讓解題目標非常明確,體現了解析幾何問題的本質.

解法2 設P(x0,y0),A(x1,y1),B(x2,y2),點P到直線l的距離為h,則

因為|AP|·S2=|BP|·S1,

所以|AP|·|BQ|=|BP|·|AQ|.

(方向1)由角平分定理,得PQ為∠APB的角平分線,則∠APQ=∠BPQ.

所以k1=-k2.

即k1+k2=0.

即k1+k2=0.

評注此法方向1使用角平分線定理進行處理,方便快捷,說明解析幾何的問題本質還是屬于幾何問題,使用相關幾何性質求解問題能起到事半功倍的效果.方向2使用弦長公式進行求解,符合解析幾何問題的特點,屬于通性通法.

解法3 設P(x0,y0),A(x1,y1),B(x2,y2),直線AP與BP的斜率分別為k1與k2(k1≠k2),則

因為|AP|·S2=|BP|·S1,

所以sin∠APQ=sin∠BPQ.

即∠APQ=∠BPQ,

故k1=-k2.

即k1+k2=0.

評注此法最為直接,根據兩個三角形的特點,利用相關公式,將條件直接轉化為夾角關系,進而得到斜率之間的關系,體現了靈活運用知識解決問題的能力.

解法4 設P(x0,y0),A(x1,y1),B(x2,y2),直線AP與BP的斜率分別為k1與k2(k1≠k2),則

因為∠AQP+∠BQP=π,

即sin∠AQP=sin∠BQP,且

|AP|·S2=|BP|·S1,

所以|AP|·|BQ|=|BP|·|AQ|.

以下同解法2.

評注此法利用兩個三角形的互補角關系進行轉化,對比解法2與解法3,雖無更加便捷,但給解決此類問題提供了另一種有效方式,值得我們認真體會.

通過以上四種思路,將條件|AP|·S2=|BP|·S1轉化為條件k1+k2=0,讓解題方向更加明確.下面將從兩個角度對條件k1+k2=0進行探究.

思路1 利用韋達定理進行求解.

(1+2k2)x2-4k2x+2k2-8=0.

因為k1+k2=0,

所以(kx1-k-y0)(x2-x0)+(kx2-k-y0)(x1-x0)=0.

即2kx1x2-(kx0+y0+k)(x1+x2)+2x0(k+y0)=0.

故2y0(x0-1)k2+(x0-8)k+x0y0=0.(*)

因為點P在橢圓C上,

即(2y0k-x0)[(x0-1)k-y0]=0.

因為點P不在直線l上,

所以y0≠k(x0-1).

即k(x0-1)-y0≠0.

故2y0k-x0=0.

評注此法為通法,難點在于含參多、計算量大,尤其是后面的因式分解技巧性較強,因此,在平時的練習中,需多總結一些優化運算的方法,熟練常規運算,提高運算能力.

思路2 利用“齊次化”進行處理.

解法2 設直線l的方程為

m(x-x0)+n(y-y0)=1,

(△)

因為點P在橢圓C上,

2(y-y0)2+2x0(x-x0)+4y0(y-y0)+(x-x0)2=0.

所以2(y-y0)2+[2x0(x-x0)+4y0(y-y0)]·[m(x-x0)+n(y-y0)]+(x-x0)2=0.

因為k1+k2=0,

即2nx0+4my0=0.

評注此法為巧法,通常解析幾何問題涉及斜率之和或之積時,均可使用“齊次化”處理,但使用此法時需注意直線方程的形式以及曲線方程的變形,都要符合這種方法的要求.

4 試題推廣

根據上述求解過程,將橢圓方程一般化,同時推廣到雙曲線、拋物線、圓,得到以下幾個結論.

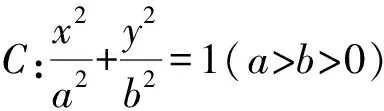
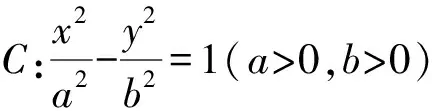
以上結論的證明過程與試題求解過程類似,在此不再贅述.

5 結束語

解析幾何問題包羅萬象,對于基礎知識、基本方法、基本思想學生容易掌握到位.但解析幾何大題涉及許多關聯知識和一些技巧性較強的方法,學生很難突破.解析幾何是高考的熱點與難點內容,因此,在平時的教學中,必須舍得花時間和精力去深入研究,總結方法與規律,積累基本經驗,開拓解題思路,不斷提升解題技能.解析幾何中涉及斜率之和或之積問題入口很寬,求解方法多樣,對加深理解解析幾何的本質、提升數學思維與核心素養大有裨益[1].