一道2023年北京大學寒假學堂試題的求解與拓廣

張志剛

(山東省寧陽縣復圣中學,山東 泰安 271400)

圓錐曲線中弦張直角問題歷來是高考、競賽、高校強基計劃測試的熱點,主要考查曲線方程、定點、面積、最值等相關問題.本文以一道2023年北京大學優秀中學生寒假學堂測試題為例,通過類比和推廣,得到圓錐曲線中弦張直角的一般性結論,并通過實例介紹結論的應用.

1 試題呈現

本題是直線與雙曲線的位置關系問題,考查直觀想象、數學運算、邏輯推理等核心素養,試題設計簡潔清新,思維跨度較大,頗具綜合性、挑戰性和選拔性.

2 試題解答

在Rt△OPQ中,設O到直線l的距離為d,則

故選C.

在Rt△OPQ中,設O到直線l的距離為d,則

故選C.

3 試題拓廣

3.1 張直角弦上高的垂足的軌跡

結論3 若直線l與拋物線y2=2px(p>0)交于P,Q兩點,且OP⊥OQ,OM⊥PQ,則垂足M的軌跡是圓(x-p)2+y2=p2(x≠0).

下面從原點和定點等特殊點出發,再推廣至一般的定點,探討圓錐曲線的弦張直角的充要條件.

3.2 弦對原點張直角的充要條件

得b2t2(m2-a2)x2+a2(t2m2-b2)y2+2ta2b2xy=0.

設直線OP,OQ的斜率分別是k1,k2,則k1,k2是方程a2(t2m2-b2)k2+2ta2b2k+b2t2(m2-a2)=0的兩個實數根,由根與系數的關系得

整理,得(a2+b2)t2m2=a2b2(1+t2).

結論5的證明可仿照結論4完成,不再贅述.

將以上結論一般化,即得結論6.

結論6 若直線l:mx+ny=1與有心二次曲線Ax2+By2=1(AB≠0)交于P,Q兩點,O為原點,則OP⊥OQ的充要條件是A+B=m2+n2.

Ax2+By2=(mx+ny)2.

即(B-n2)y2-2mnxy+(A-m2)x2=0.

設直線OP,OQ的斜率分別是k1,k2,則k1,k2是方程(B-n2)k2-2mnk+A-m2=0的兩個實數根,由根與系數的關系得

即A+B=m2+n2.

設P(x1,y1),Q(x2,y2),由根與系數的關系,得

所以x1x2+y1y2=0.

整理,得A+B=m2+n2.

綜上,OP⊥OQ的充要條件是A+B=m2+n2.

3.3 弦對頂點張直角的充要條件

結論9 若直線l與拋物線y2=2px(p>0)交于P,Q兩點,A為拋物線的頂點,則AP⊥AQ的充要條件是直線l過點(2p,0).

結論7、8的證明可參考文獻[1],下面給出結論9的證明.

證明設直線l:mx+ny=1,代入y2=2px,得

y2=2px(mx+ny),

設直線OP,OQ的斜率分別是k1,k2,則k1,k2是方程k2-2pnk-2pm=0的兩個實數根,由根與系數的關系得k1k2=-2pm.

又OP⊥OQ,所以-2pm=-1,即2pm=1.

-2pny=x-2p.

故直線l過點(2p,0).

把結論7、8中的右頂點改為其他頂點,把結論9中開口向右改為其他開口方向,也有類似結論,請讀者自證.

3.4 弦對定點張直角的充要條件

圖1 結論10示意圖

證明設P(x1,y1),Q(x2,y2),

(a2+b2k2)y2+2b2mky+b2m2-a2b2=0.

由根與系數的關系,得

代入上式并整理,得

解得m=x0-ky0(舍去)或

故直線l的方程為

則直線l的方程為y=nx-t(nx0+y0).

由根與系數的關系,得

又y1=nx1-t(nx0+y0),

y2=nx2-t(nx0+y0),

所以y1+y2=n(x1+x2)-2t(nx0+y0),

y1y2=[nx1-t(nx0+y0)][nx2-t(nx0+y0)]

=n2x1x2-nt(nx0+y0)(x1+x2)+t2(nx0+y0)2

故MP⊥MQ.

圖2 結論11示意圖

結論12 如圖3,若直線l與拋物線y2=2px(p>0)交于P,Q兩點,點M(x0,y0)為拋物線上異于P,Q兩點的一個定點,則MP⊥MQ的充要條件是l過定點N(2p+x0,-y0).

圖3 結論12示意圖

4 結論的應用

解析由結論1知,垂足M的軌跡是圓

(1)求橢圓的方程及離心率;

(2)由(1)得A(3,0).

設直線PQ的傾斜角為θ,由結論4得

例3 (2007年高考山東卷理科第21題)已知橢圓C的中心在坐標原點、焦點在x軸上,橢圓C上的點到焦點距離的最大值為3,最小值為1.

(1)求橢圓C的標準方程;

(2)若直線l:y=kx+m與橢圓C相交于A,B兩點(A,B不是左右頂點),且以AB為直徑的圓過橢圓C的右頂點.證明:直線l過定點,并求出該定點的坐標.

圖4

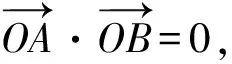
(x-2)2+y2=4(x≠0).

解析由結論1知,

由基本不等式,得

5 結束語

高考題實際上是將必然有的一些結論特殊化,化一般為特殊,讓學生用所學知識來解決必然成立的問題,只有學生把方法、知識、技巧融為一體,做題時旁征博引,融會貫通,以不變應萬變,解一題而曉一類題,這樣勢必會得出一系列理想的結論.