類星艦飛行器翻轉著陸軌跡優化

魯 鵬，李雅軒，劉新福

（北京理工大學宇航學院，北京，100081）

0 引 言

航天運輸系統是開展空間活動的核心支撐，是發展航天事業、建設航天強國的基本前提，是加速發展空間科學技術、和平開發空間資源和維護國家空間安全的重要保障［1］。近年來，隨著人類空間資源開發需求的快速增長，可重復使用運載器受到了全球的廣泛關注，世界各主要航天大國積極開展了相關的理論研究和工程實踐［2］。

瞄準星際移民和深空探測的目標，美國太空探索技術公司（SpaceX）研制了名為星艦（Starship）的新一代可重復使用航天運輸系統。2016 年9 月，SpaceX 公司正式對外公布了“星際運輸系統”方案［3］。此后，星艦設計方案經歷了多次重大改進和演化。自2020 年起，通過開展密集的飛行測試，SpaceX 公司逐步掌握了150 m 低空懸停、10 km 高空飛行、翻轉機動和垂直定點軟著陸等關鍵技術，項目取得重大進展。值得關注的是，星艦采取了與傳統航天器截然不同的著陸方式：著陸前，星艦采用90°左右大攻角飛行，在視覺上以腹部平拍的姿態向地面飛行；接近地面時，星艦發動機開機進行推力矢量控制，聯合首尾四個氣動舵，完成姿態由水平向垂直的快速翻轉，并控制星艦減速和修正位置誤差，實現定點軟著陸［4］。圖1展示了該特殊的著陸過程。這種獨特的著陸方式對飛行器的軌跡優化設計提出了新的挑戰。大范圍的姿態機動和復雜的約束條件必須在優化設計翻轉著陸飛行軌跡時得到充分的考慮。

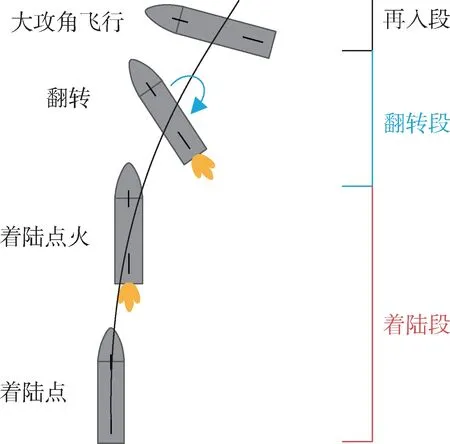
圖1 類星艦飛行器翻轉著陸過程示意Fig.1 The flipping and landing process of a starship-like vehicle

近年來，凸優化方法被廣泛地應用于飛行器軌跡優化設計，特別是在解決星際探測器、運載火箭等常規航天器的著陸軌跡優化問題時發揮積極作用［5］。美國噴氣推進實驗室的A??kme?e 等［6］通過使用無損松弛和變量替換等方法將帶有非凸推力約束的火星著陸軌跡優化問題轉化為凸優化問題，顯著提高了軌跡優化算法的可靠性和計算效率。Szmuk等［7］對六自由度火星動力下降制導問題進行了深入研究，通過設計序列凸優化算法計算考慮姿態動力學的著陸飛行軌跡。相比于火星著陸，因為氣動力不可忽略，運載火箭著陸在地球表面的軌跡優化問題求解難度更大。劉新福［8］將推力和攻角同時作為控制量，把對應的燃料最優著陸問題順利轉化為凸優化問題進行迭代求解，并理論證明了所采用松弛技術的有效性。楊潤秋等［9］將該研究工作拓展到飛行時間自由的問題，用高度代替時間作為自變量對優化問題進行重構，并基于序列凸優化設計了軌跡優化算法，其中使用的非線性保留技術被證實可以有效提升算法收斂性。

盡管上述方法能夠有效解決常規航天器的著陸軌跡優化問題，但對類星艦飛行器的翻轉著陸軌跡優化并不太適用。原因在于類星艦飛行器在滑翔段和著陸段之間存在獨特的翻轉過程。大范圍的姿態機動導致類星艦飛行器不能被簡單地處理為質點模型，而必須在設計著陸軌跡時考慮姿態動力學和因姿態控制產生的復雜約束條件。但是，目前針對此類軌跡優化問題的研究非常有限。

本文針對類星艦飛行器的翻轉著陸軌跡優化問題進行了深入研究。首先根據類星艦飛行器在翻轉著陸階段的飛行力學特征和任務特點，建立考慮姿態機動和典型約束條件的翻轉著陸軌跡優化問題。然后研究將該優化問題通過凸化方法轉化為凸優化問題，進而設計迭代算法序列求解。通過提供合理的初值、引入虛擬控制和在目標函數中懲罰信賴域半徑等方法，該迭代算法表現出良好的收斂性。針對發動機擺角振蕩問題，本文提出將發動機擺角響應引入動力學，這種處理被證實能夠有效抑制發動機擺角振蕩，并有利于迭代算法的收斂。此外，依托軌跡優化算法，本文亦分析了發動機個數和優化目標選取等因素對類星艦飛行器翻轉著陸過程的影響，相關數值結果可以為類星艦飛行器的翻轉著陸軌跡優化設計提供參考。

1 翻轉著陸軌跡優化問題

1.1 動力學建模

本文將研究類星艦飛行器在二維平面內考慮一個姿態角的翻轉著陸軌跡優化問題。再入過程中飛行器控制能力強，通常可使飛行器再入終端速度矢量和著陸點位于同一垂直平面內，而著陸過程中的側向運動通常會消耗額外燃料，因此在進行類星艦飛行器軌跡優化時可以忽略側向運動。實際飛行時，著陸過程中的側向位置誤差可以通過控制進行修正。構造類星艦飛行器翻轉著陸軌跡優化問題時會使用到著陸坐標系Oxy和體坐標系Obxbyb，如圖2所示。

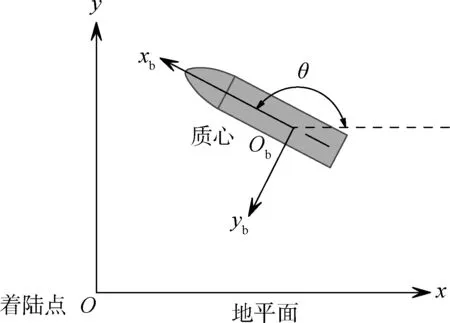
圖2 著陸坐標系Oxy和體坐標系Obxb ybFig.2 The definition of landing coordinate system Oxy and the body-fixed coordinate system Obxb yb.

圖3a 展示了飛行器翻轉著陸過程受力分析結果，根據牛頓第二定律建立動力學方程。為了避免在問題求解時出現數值問題，需要對動力學方程中的物理量進行無量綱化處理。長度的無量綱系數為飛行器初始高度ry0，速度無量綱系數為ry0g0（g0是地球表面重力加速度），時間無量綱系數為ry0g0，質量無量綱系數為初始質量m0。著陸坐標系下，無量綱的飛行器翻轉著陸的動力學方程，記為x?(t) =f(x(t)，u(t))，如下：

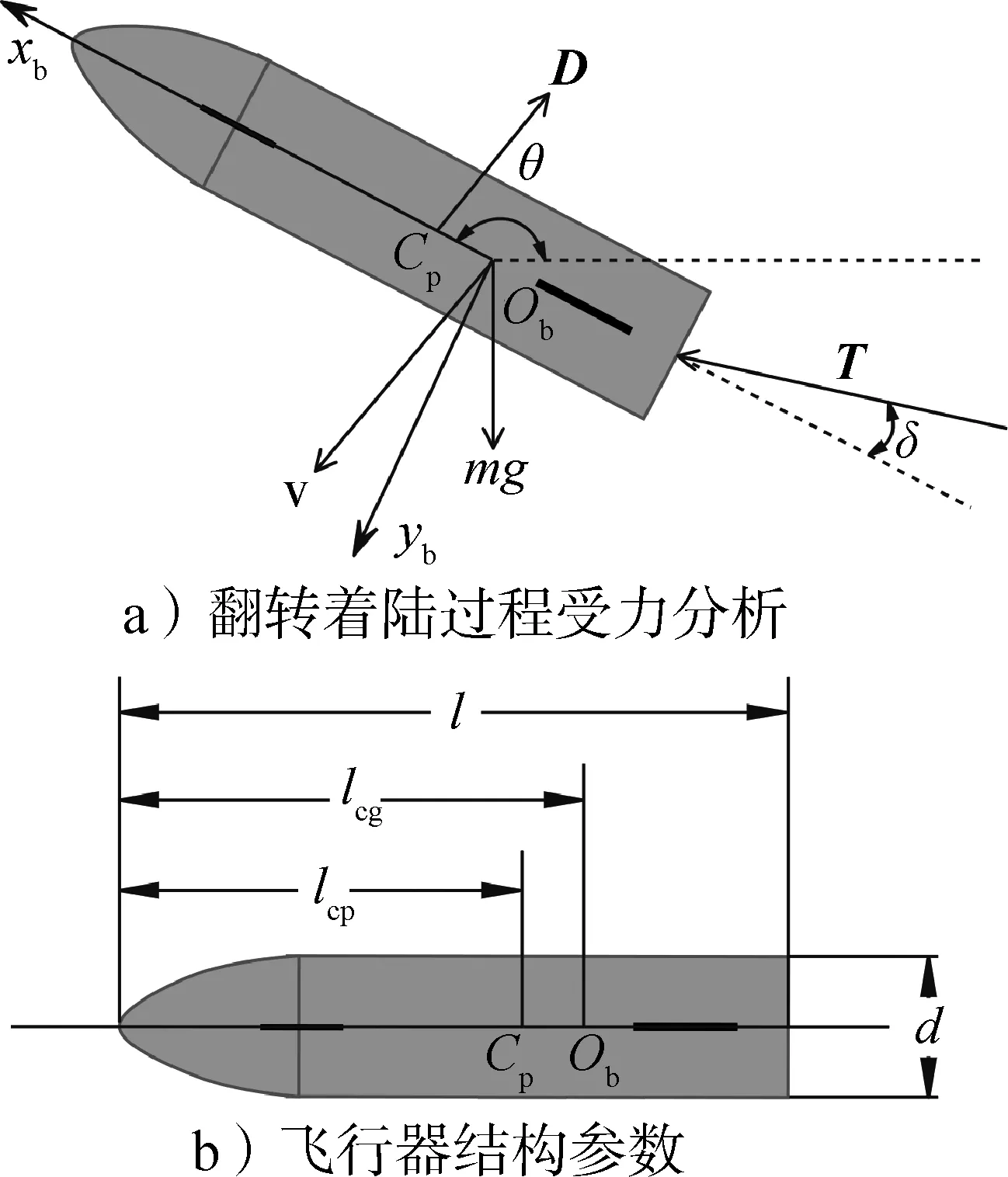
圖3 飛行器受力分析和結構參數Fig.3 Force analysis and structural parameters of the vehicle

式中r∈R3為飛行器位置矢量；v∈R3為飛行器速度矢量；m為飛行器質量；T為發動機推力矢量；T為推力矢量的模，T=‖T‖；D為氣動阻力矢量；g為重力加速度矢量；θ為飛行器俯仰角（定義見圖2）；ω為俯仰角速度；MT為推力產生的力矩；MD為阻力力矩；Jz為飛行器繞質心的轉動慣量；αe為質量消耗率，αe=-1Isp，Isp為發動機比沖；δ為發動機擺角；δd為δ的響應；Td為一階慣性環節的無量綱時間常數。本文將發動機擺角視為控制變量，它同時控制位置和姿態，進行軌跡優化時會導致嚴重的發動機擺角振蕩。鑒于此，本文將發動機擺角響應引入動力學（見式（6））。數值仿真結果表明，這一思路將有效抑制發動機擺角振蕩現象，進而提高了2.3 節設計的軌跡優化算法的收斂性。x為狀態變量，x=[rTvTθ ω m δd]T，u為控制變量，u=[T δ]T。本文將動力學投影在著陸坐標系中，因此無量綱的推力T、阻力D以及相應推力力矩MT和阻力力矩MD的計算公式如下：

1.2 其它約束條件

飛行器翻轉著陸軌跡優化不僅受到動力學方程的約束，還有端點約束和過程約束，接下來詳細介紹這些約束。

飛行器初始狀態約束可以表述成Φ= 0 的形式。本優化問題給定初始位置r(1)0、速度v(1)0、俯仰角θ(1)0、俯仰角速度ω(1)0和初始質量m(1)0，本文使用上標“（1）”標記翻轉段對應的量，使用上標“（2）”標記著陸段對應的量。因此Φ具體表達式如下：

翻轉著陸過程中飛行器不能有向上的速度，即豎直速度vy不能為正，因此得到速度約束：

為了保證翻轉過程中飛行器姿態在合理范圍，保證著陸過程飛行器垂直著陸，翻轉著陸過程施加如下關于俯仰角的邊界約束：

考慮到飛行器在載人時的舒適性和姿態控制系統的能力，姿態角速度不能超過最大值ωmax，即有：

發動機的最大擺角記為δmax，故擺角需要滿足：

發動機擺角速度不能超過最大值δ?max，可以通過約束發動機擺角響應的變化率δ?d實現對發動機擺角速度的限制，由式（6）可知，需引入如下限制發動機擺角速度的約束：

式中n為發動機個數，n∈N+。

為了方便垂直著陸，每個時刻飛行器和著陸點連線與豎直方向的夾角不能大于給定角度γgs，這就需要添加下滑道約束：

式中ry為位置矢量在著陸坐標系y軸方向的分量。該下滑道約束是一個二階錐約束。

過程約束（12）～（18）可以改寫為如下不等式約束：

末端等式約束可以表示為E=0 的形式，本優化問題中飛行器將著陸到給定位置r(2)f，與此同時末端速度到達給定值v(2)f、俯仰角到達θ(2)f并且俯仰角速度到達ω(2)f。因此，E具有如下形式：

由于燃料有限，終端質量需要滿足m(2)(t(2)f)≥mdry，mdry為燃料耗盡時飛行器的質量。

飛行器在翻轉段和著陸段交接點處的飛行狀態應當連續，連接約束可以表示為Ψ=0，其中：

翻轉段耗時、著陸段耗時和翻轉著陸段總飛行時間滿足約束：

式中tmin為總飛行時間下界；tmax為總飛行時間上界。

1.3 翻轉著陸軌跡優化問題

在優化類星艦飛行器翻轉著陸的軌跡時，為節約燃料，同時保證翻轉結束時飛行器高度不能太低，設計了如下目標函數：

式中μ為懲罰系數，調節μ可以改變翻轉段結束時飛行器的離地高度。當μ= 0 時，該優化目標將轉化為翻轉著陸過程燃料最優。本文3.4 節將詳細探討該懲罰系數的取值對翻轉著陸軌跡的影響。

綜上所述，可以構造翻轉著陸軌跡優化問題P0：

問題P0的本質是多階段飛行時間自由的最優控制問題。因為動力學約束非線性很強，P0 求解難度較大。

2 凸優化求解

本節將介紹使用改進的序列凸優化（Sequential Convex Programming，SCP）算法求解飛行時間自由的類星艦飛行器翻轉著陸軌跡優化問題的方法。雖然序列凸優化算法無法保證收斂，但是可以使用一些方法提高其收斂性。為了提高收斂性，求解問題P0時引入虛擬控制，懲罰信賴域半徑［10］，并給出了初值選取方法。為了公式的簡潔性，本節不再添加區分翻轉段和著陸段的上標“（i）”。

為了將飛行時間自由的最優控制問題P0轉化為等價的飛行時間固定的最優控制問題，引入變量τ=(t-t0)/Δt，其中Δt=tf-t0表示該階段耗時，t0是該階段的初始時間，tf是該階段的終端時間。將動力學方程轉換為以τ∈[0，1]為自變量的形式：

式中 上標“'”表示變量對τ求導。狀態變量和控制變量是t的函數，同樣也是τ的函數，故有：

當以τ作為自變量時，初始狀態約束是τ= 0時的狀態約束，終端狀態約束是τ= 1時的狀態約束。

2.1 線性化

線性化可以將上述非線性動力學方程（25）轉化為線性動力學方程。將方程（25）在上一次迭代得到的解附近泰勒展開并保留常數項和一階項，用展開后的線性方程近似原本的非線性動力學方程。這里將上一次迭代得到的解記為z[k](τ) ?[(x[k])T(u[k])T]T，時間記為Δt[k]，那么在z[k](τ)和Δt[k]附近線性化方程（25），可以得到如下線性動力學方程：

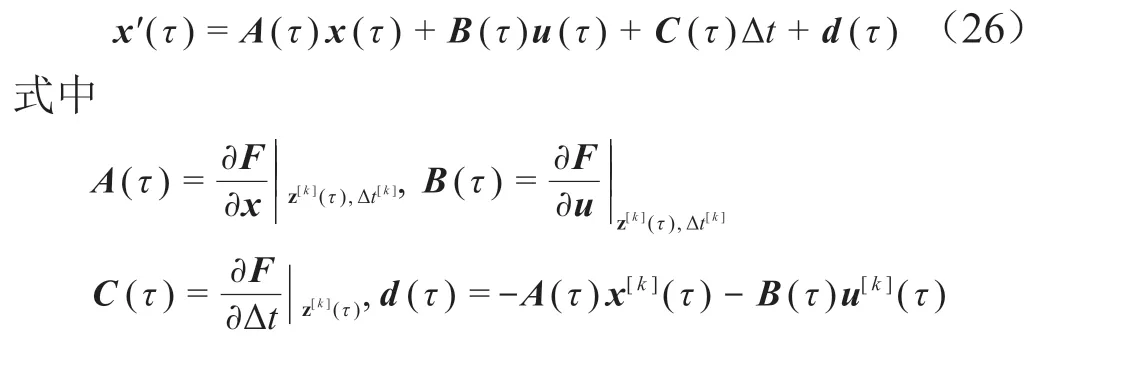
為了構造凸優化問題，除了動力學方程外其它非凸約束也需要進行線性化處理，例如：假設sn(z)是關于z的非凸函數，則如下約束是非凸約束：

使用一階泰勒展開，略去高階項，sn(z(τ))≤0 可以由如下線性不等式約束近似：

而問題P0 中除了動力學約束外沒有其它非凸約束。

2.2 離 散

為了將連續時間最優控制問題轉化為非線性規劃問題，需要對連續時間最優控制問題進行離散。將τ所在的區間［0，1］離散成N份，0 =τ0<τ1< …<τN=1，式中τ0，τ1，…，τN是離散節點，與自變量對應的狀態 離 散 點 記 為x0，x1，…，xN，控 制 離 散 點 記 為u0，u1，…，uN。離散動力學的數值方法有很多［11］，包括歐拉法、梯形法、零階保持器和一階保持器等，本文使用梯形法。線性化后的動力學方程（26）經梯形法離散得到線性等式：

式中hj=τj+1-τj。

動力學以外的其它約束，例如sn(z(τ)) ≤0，離散形式是每個離散節點上都滿足相應約束：

2.3 虛擬控制和懲罰信賴域

非線性動力學和其它非線性約束經過線性化后，可能使原本可行的問題變成不可行的問題。為了解決由線性化導致的問題不可行，在動力學方程（29）上添加虛擬控制。離散的動力學方程（29）添加虛擬控制vc(τ) ∈R8后 得 到 等 式 約 束（31）， 記 為

式中vcj=vc(τj)，虛擬控制vcj可以保證任意下一個節點處的狀態xj+1都是可以達到的。需要注意，如果序列凸優化算法收斂時虛擬控制的值不為零，則得到的結果就不滿足線性化前的動力學約束。為了使程序收斂時虛擬控制為零，需要在目標函數中增加關于虛擬控制的懲罰項Jvc，并且需要為虛擬控制設置一個較大的懲罰系數λvc，本文使用的Jvc如下：

為了保證線性化的合理性，需要添加信賴域約束。本文使用可變信賴域，信賴域作為懲罰項放在目標函數中，即在目標函數中添加關于信賴域的懲罰項Jtr：

式中λtr為懲罰系數。這種以添加懲罰項的方式處理信賴域半徑的方法通常可以使問題收斂得更快。λtr取值一般較小，因為當該值較大時，前后兩次迭代的結果相差較小，會導致序列凸優算法收斂速度變慢，并且很容易收斂到初值附近的可行解。

至此，可以得到時間自由的兩階段軌跡優化問題P0被凸化后的優化問題P1。本文在翻轉段將τ離散為N1等份，在著陸段將τ離散為N2等份。

序列求解凸優化問題P1，當Jvc< ?vc并且Jtr

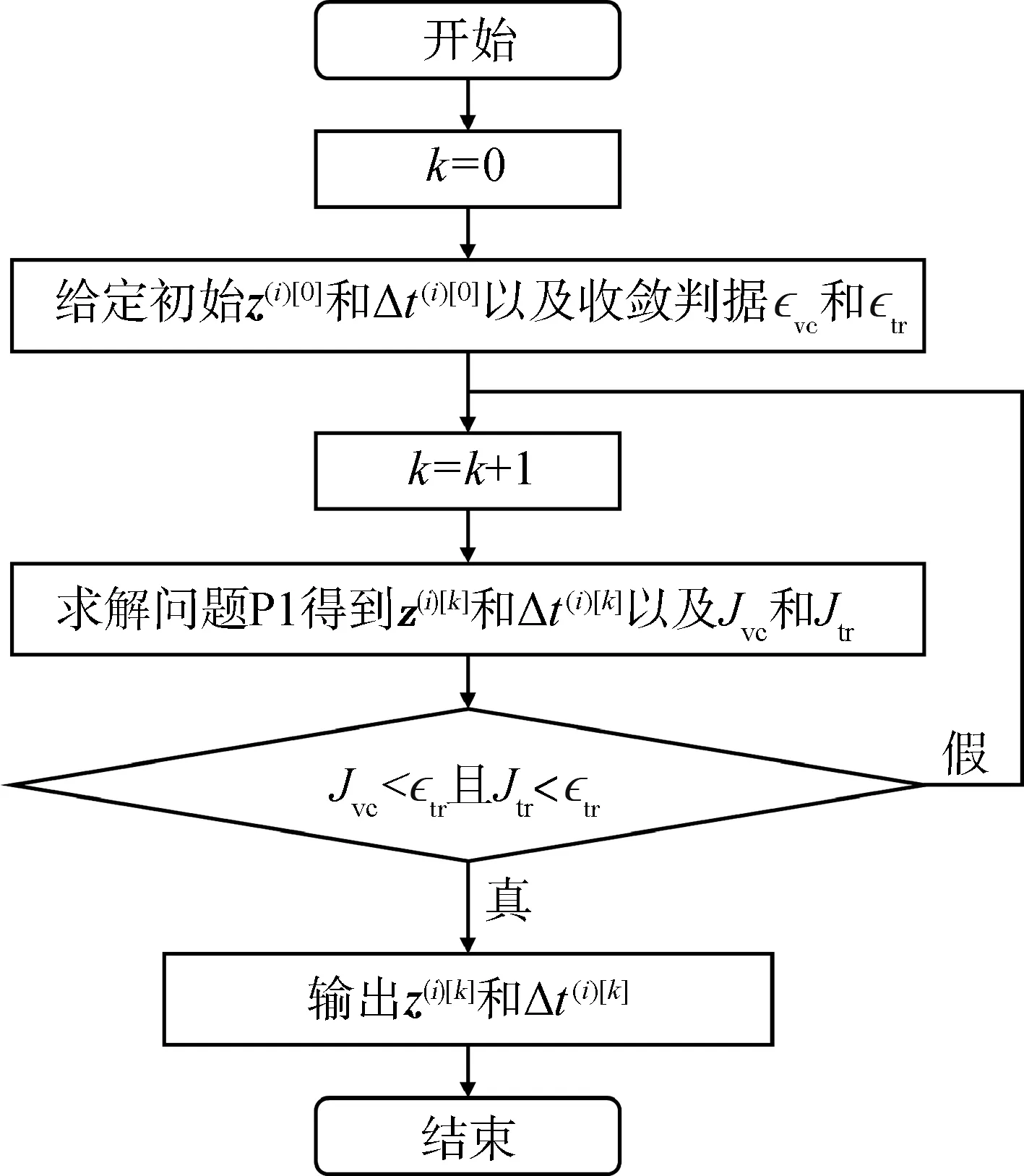
圖4 軌跡優化算法流程Fig.4 Flow chart of trajectory optimization algorithm

2.4 初值選取

對于動力學和其它約束較為簡單的優化問題，在使用序列凸優化算法求解時，通常可以直接使用線性初值。而對于本文構造的動力學非線性很強的優化問題，由于線性初值表現不佳，很容易造成算法1收斂慢或無法收斂的情況。為了提高算法1的收斂性，在這里給出一種選取更好初值的方法。

在求翻轉段初值時，先忽略翻轉過程中氣動阻力產生的力矩，然后給定發動機推力和擺角，積分到俯仰角等于給定的θs且垂直速度等于vys時結束，積分結果作為翻轉段初值。θs取90°附近的值便于后續垂直著陸。速度vys不能太大，需要保證著陸時速度能減到0。在計算著陸段初值時，求解在問題P0著陸段基礎上簡化得到的凸優化問題，以簡化問題的解作為著陸段初值。具體來說就是給定簡化問題的著陸時間，忽略氣動力，關于速度的動力學方程不考慮質量變化，不考慮姿態動力學和發動機擺角，并滿足部分過程和終端約束，即求解如下凸優化問題：

式中x0取翻轉段末端狀態；γT為推力方向和y軸間允許的最大夾角；ε為松弛變量；不使用ε計算初值的優化問題可能無解。 上述優化問題中不包括θ，ω，δ，δd。俯仰角θ根據推力方向計算，引入推力方向約束就是為了避免通過推力方向計算的俯仰角過大，ω通過對θ進行差商得到，δ(t) =δd(t) =0。求解上述凸優化問題可以得到一個較好的初值，且計算效率高。仿真部分將比較本初值選取方法和線性初值選取方法對算法1的影響。

3 數值仿真

本節將通過數值仿真來分析類星艦飛行器翻轉著陸問題的特性，希望能為相關任務設計提供一定的參考。本節數值仿真主要參考星艦公開的參數［13］，部分重要參數見表1。本文在實現算法1 時使用了凸優化求解器ECOS［14］。

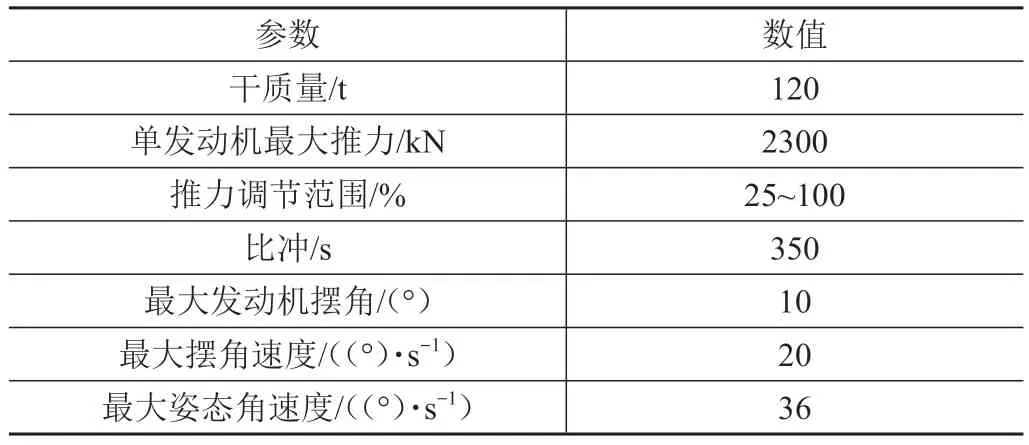
表1 飛行器參數Tab.1 Vehicle configurations

飛行器高l= 50 m，lcg= 0.6l，lcp= 0.55l。飛行器初始位置r0=[360 1200]Tm，初始速度v0=［-18.82-106.73]Tm/s，θ0= 170°，ω0= 0（°）/s，m0= 132 t。用于計算的初值θs= 80°，vys=-20 m/s。翻轉過程使用3 臺發動機，著陸使用2 臺發動機。末端位置rf=[0 0]Tm，末端速度vf=[0 -0.1]Tm/s，θf= 90°，ωf=0（°）/s。邊界約束中θ(1)max= 170°，θ(1)min= 45°，θ(2)max=105°，θ(2)min= 75°。算 法1 參 數：N1= 40，N2= 50，λvc= 103，λtr= 5 × 10-5，收斂判據?vc= 1 × 10-8，?tr=1 × 10-8，目標函數中μ=0.3。

使用圖4算法求解該算例時，迭代7次收斂，翻轉段耗時2.43 s，著陸段耗時13.61 s，整個過程消耗燃料9.773 t。圖5 展示了優化結果：圖5a 展示了翻轉著陸過程的路徑點和推力方向。圖5b展示了俯仰角和俯仰角速度的變化，最大的俯仰角速度小于給定上界36 。優化的控制量繪制在圖5c和圖5d中，由于目標函數考慮了讓翻轉過程高度差較小，所以翻轉時先以最大推力和最大擺角加速翻轉，接著使用小推力翻轉，同時擺角開始減小為接下來減小俯仰角速度做準備，然后在著陸段開始時以最大推力和最小擺角為翻轉過程減速，即降低俯仰角速度。整個翻轉著陸過程推力幾乎是砰—砰（bang-bang）形式，發動機擺角不大于10°。

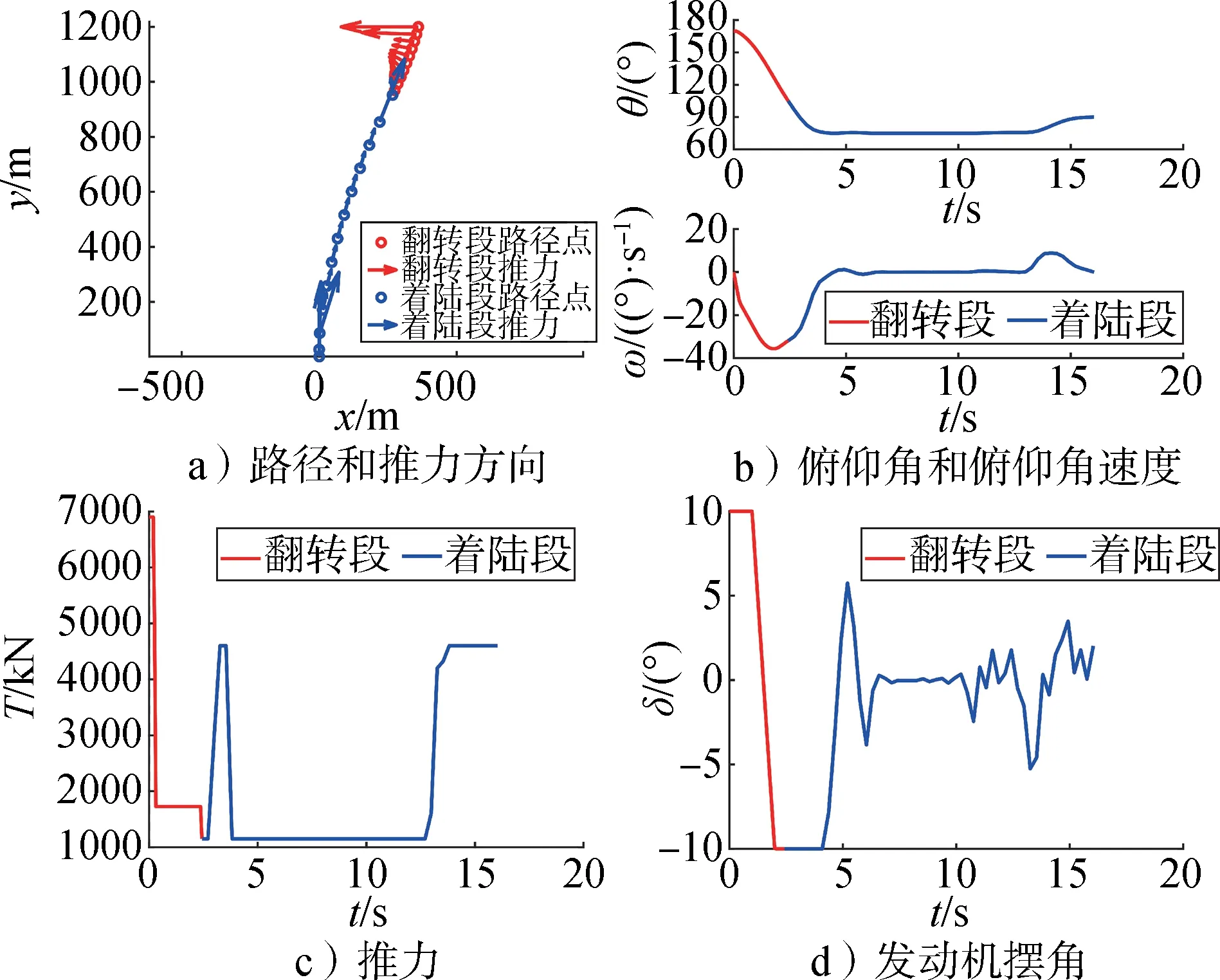
圖5 飛行器翻轉著陸軌跡優化結果Fig.5 Optimized results of the flipping and landing trajectory of the Starship-like vehicle

接下來改變部分仿真條件，深入研究類星艦飛行器翻轉著陸軌跡優化問題的性質，并將對應結果與圖5中的結果進行比較。

3.1 不同初值選取方法的影響

對于復雜的軌跡優化問題，初值選取對于序列凸優化算法的收斂性有較大影響。這一小節將比較線性初值和本文初值選取方法對算法1的影響。

使用線性初值，算法1 迭代9 次后收斂，比使用本文初值選取方法多了2次迭代，從圖6a可以看出使用本文初值收斂更快。翻轉段耗時2.38 s，著陸段耗時14.02 s，整個過程消耗燃料9.947 t，比使用本文初值多消耗174 kg。圖6c 展示了推力剖面的對比，使用線性初值時，推力不是砰—砰形式。此外，使用線性初值時，發動機擺角剖面也不如使用本文初值時那么平緩，如圖6d所示。大量仿真實例表明算法1使用本文初值選取方法比線性初值收斂性更好，在有些使用線性初值無法收斂的情況下，使用本文初值也能收斂。本文初值選取方法不僅提高了算法的收斂性，而且優化的推力和發動機擺角剖面更適合工程使用。

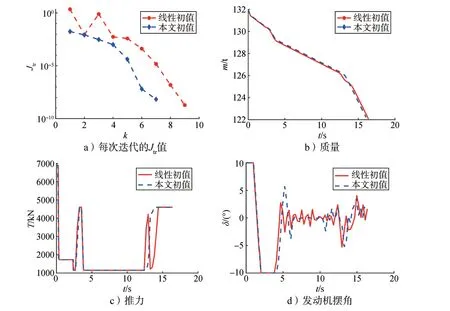
圖6 使用線性初值和本文方法確定的初值的結果對比Fig.6 The comparison between the results with linear initial guess or the initial guess obtained by the proposed method

3.2 發動機擺角響應相關約束的作用

在3.1 節中說明了引入發動機擺角響應和相關約束的作用——避免求解的發動機擺角振蕩。這一小節將給出不使用發動機擺角響應δd而其它部分都相同時的計算結果。

如前所述，使用δd的算例迭代7 次收斂，而不使用δd的算例迭代20次未收斂。圖7給出了使用和不使用δd計算結果的對比（不使用擺角響應的算例20次迭代未收斂，這里畫了第20次迭代中的解），圖7a和圖7c顯示兩個算例計算的推力和速度剖面幾乎相同，但是發動機擺角差別較大，不使用δd的算例得到的發動機擺角（見圖7b 中紅色實線）著陸前出現了劇烈的振蕩。從圖7d可以看出不使用δd時，Jtr還未小于?tr就不再減小，因此不使用δd的算例沒有收斂。發動機擺角劇烈振蕩是此算例不好收斂的主要原因。

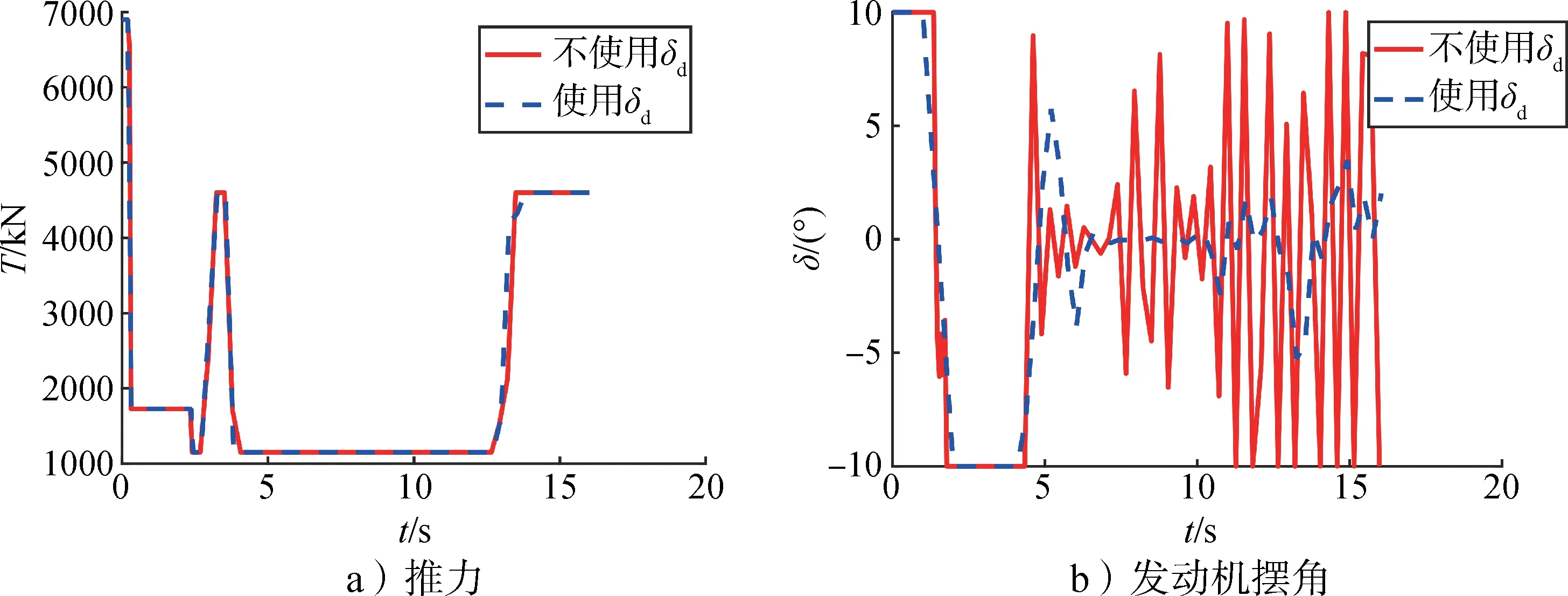
圖7 不使用和使用擺角響應約束求解結果的對比Fig.7 The results solved with and without δd

3.3 著陸使用發動機臺數的影響

仿真使用的飛行器的發動機推力較大，足以實現單臺發動機著陸。這一小節給出單臺發動機和兩臺發動機著陸時的對比結果。翻轉段仍然使用三臺發動機。

使用單臺和兩臺發動機著陸的算例都是迭代7次收斂。圖8展示了使用單臺和兩臺發動機著陸時優化的控制量，兩個算例推力變化趨勢相近，兩臺發動機著陸時大推力持續時間更短。單發動機著陸消耗燃料10.727 t，兩臺發動機著陸消耗燃料9.773 t，少消耗954 kg燃料。由此可見飛行器的推力設計對其著陸燃料消耗也是有一定影響的。

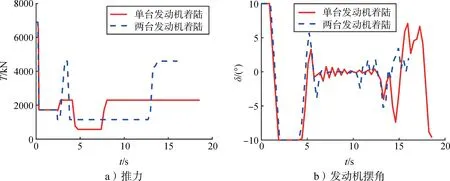
圖8 單臺發動機和兩臺發動機著陸的控制量對比Fig.8 The differences of controls between one-engine landing and two-engine landing

3.4 先翻轉再著陸和邊翻轉邊著陸的比較

上文的仿真算例中，目標函數中的懲罰系數μ都取0.3，當目標函數中μ取0時目標函數就變成了最省燃料，因為不考慮對翻轉過程高度差的優化，可能出現翻轉剛結束飛行器就接近地面的情況，這里把這種優化目標對應的優化問題P0稱為邊翻轉邊著陸問題；μ= 0.3 時目標函數表示先翻轉再著陸的同時節省燃料，這種優化目標對應的問題P0就是本文主要討論的先翻轉再著陸問題。本節將通過仿真比較兩種著陸方式的結果。

先翻轉再著陸和邊翻轉邊著陸兩個算例都迭代7 次收斂，邊翻轉邊著陸時燃料消耗8.844 t，比先翻轉再著陸少消耗929 kg燃料。圖9展示了兩個算例的仿真結果對比。圖9a是飛行器俯仰角和俯仰角速度變化曲線，可以看出邊翻轉邊著陸（μ= 0）時翻轉過程變長，翻轉過程變慢。圖9b 顯示了質量變化，邊翻轉邊著陸更省燃料，因為其目標函數就是最省燃料。圖9c 和圖9d 是兩個算例推力和發動機擺角的對比。邊翻轉邊著陸的前期使用最小推力，因為不需要快速翻轉；著陸前先最小推力再最大推力。這個邊翻轉邊著陸的算例中翻轉段耗時較短，有些算例中邊翻轉邊著陸問題中翻轉過程可以占整個飛行時間的一半以上。

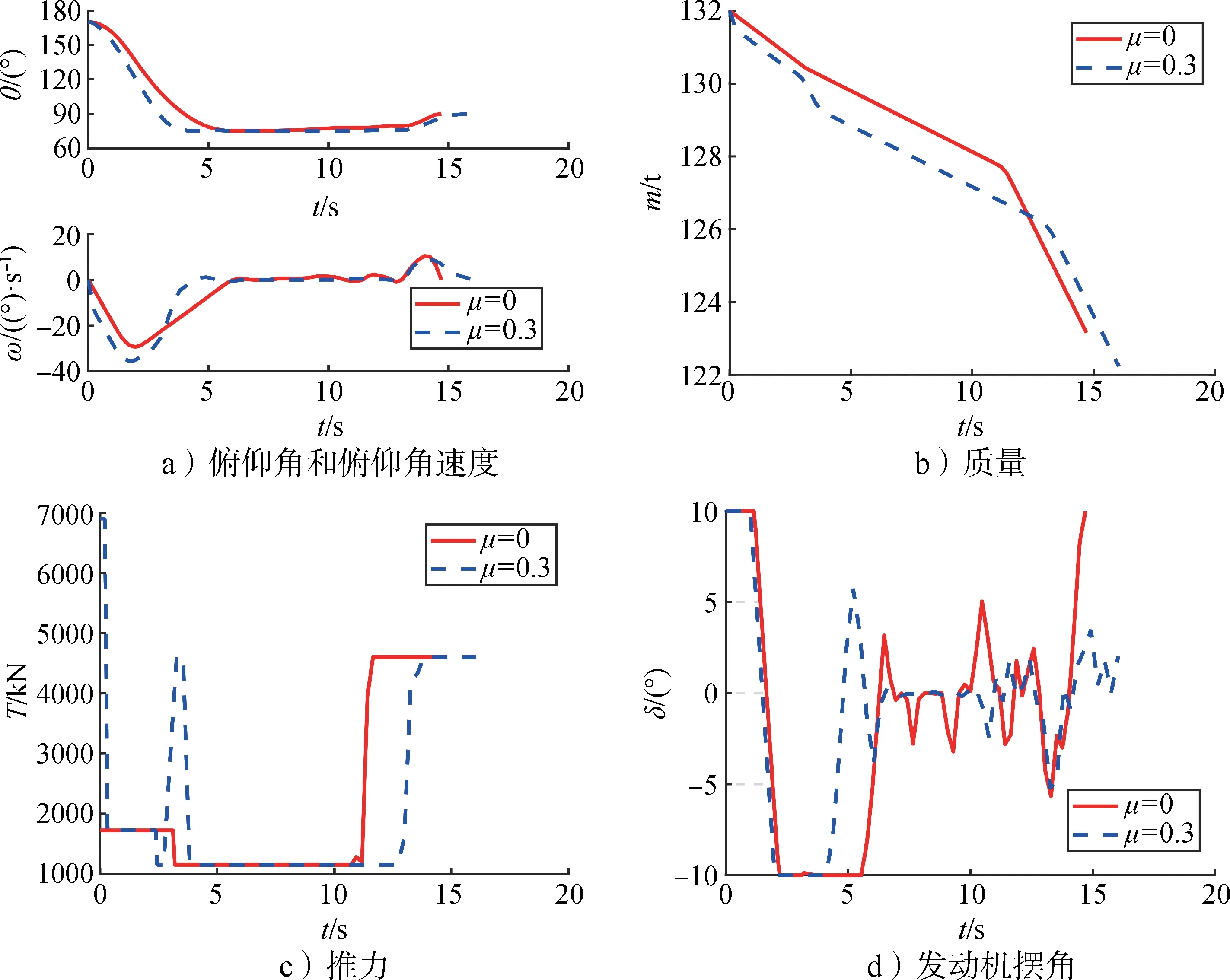
圖9 先翻轉再著陸和邊翻轉邊著陸的結果對比Fig.9 The comparison between flipping before landing case and flipping while landing case

4 結 論

本文對類星艦飛行器翻轉著陸軌跡優化問題進行了建模，設計了用于求解該問題的序列凸優化算法。為了提高算法的收斂性，該算法引入虛擬控制，懲罰信賴域，并給出了較好的初值計算方法。通過數值仿真可以發現，在求解考慮姿態動力學的類星艦飛行器翻轉著陸軌跡優化問題這樣一個強非線性軌跡優化問題時，與一般的序列凸優化算法相比本文設計的算法收斂性有很大提高。本文給出的翻轉著陸過程的軌跡優化結果可以為相關飛行器的研發提供一定的參考。