基于粒子群算法的數字控制伺服系統離線參數自尋優方法研究

楊弘棖，劉 山，許文波，張 博，李沛文

（北京精密機電控制設備研究所，北京，100076）

0 引 言

目前，航天伺服領域已經廣泛采用了數字控制器和數字控制算法，為提高伺服系統性能提供了便利的手段。當前大多采用以傳遞函數為基礎的經典控制理論對系統性能進行設計和校正。其中，機電伺服系統產品由于采用全數字控制，特性較為一致，控制參數在經過設計階段調試后一般可固化在控制算法中，生產過程中不需要更改。而電液伺服系統使用的伺服閥受到機加尺寸、裝配等環節影響，導致合格產品的靜、動態特性存在一定散布，有時需要對軟件中的控制參數進行調整，保證系統性能滿足控制系統任務書指標要求。

粒子群算法是由Kennedy 和Eberhart 等于1995 年提出的一種演化計算算法［1-2］，該方法對初值選取具有一定的魯棒性，收斂速度快，全局收斂性較好，是一種適用于工程應用的參數尋優方法［3］。目前粒子群算法已廣泛應用于函數優化、神經網絡訓練和模糊系統控制等領域。本文將其應用于數字伺服系統控制參數的離線尋優，開展了相關理論分析和仿真研究。

1 推力矢量控制伺服系統特性校正原理

某電液伺服系統的控制原理如圖1所示，使用PⅠ控制方法，結合濾波環節進行頻率特性幅值和相位的調整，其中有多項控制參數需要進行整定。

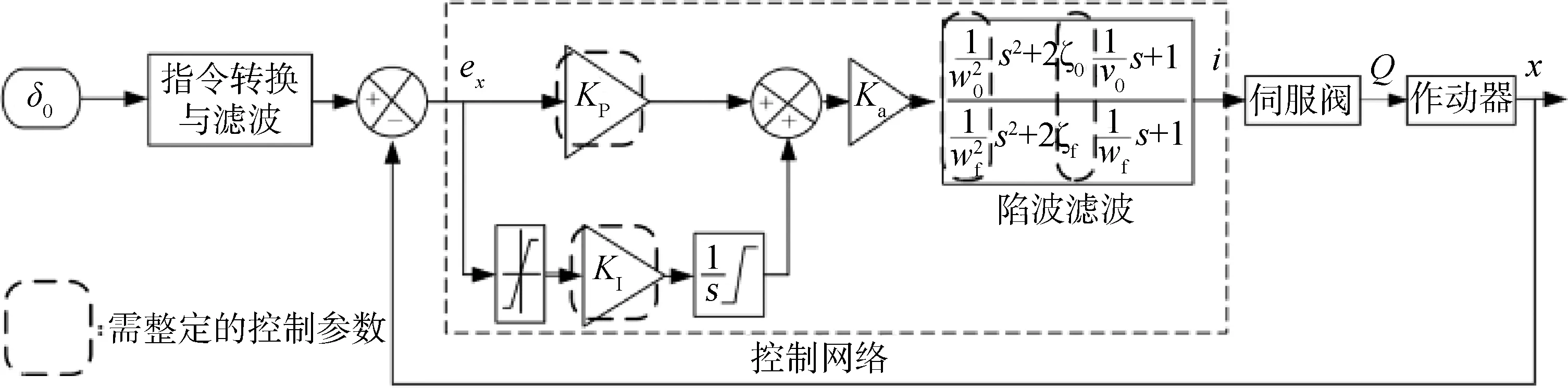
圖1 電液伺服系統控制原理Fig.1 Control principle of electro-hydraulic servo system

由于伺服閥的靜、動態特性存在一定散布，為補償伺服閥的性能差異，確保電液伺服系統的頻率特性在滿足任務書指標要求的同時具有一定余量，通常由設計人員手動調試數字控制器內的相關參數，不適用于后續大批量生產，因此，需要對伺服系統控制參數自整定方法進行研究，提高調試速度和產品合格率。

2 粒子群算法

粒子群算法通過模擬鳥群覓食過程中的遷徙和聚集，產生不可預測的群體搜索行為。在優化之前首先執行初始化：在給定的解空間內對粒子群賦予一組隨機值。給定的解空間決定了優化的速度，對粒子群進行隨機賦值的目的是在全局范圍內搜尋目標問題的最優解，確保了最優解的求解精度。個體粒子有了初始值等其他屬性后，將其代入優化目標函數進行適應度的計算。然后通過迭代尋優。迭代過程即持續更新與尋優的過程。在每一次迭代中，每個粒子通過跟蹤個體最優值Pbest（個體粒子本身在迭代過程中找尋到的最優解粒子）和全局最優值Gbest（種群中所有的粒子們在迭代過程中所找尋到的最優解）來更新自己在解空間內的位置與飛行速度。

與人工控制參數整定方法相比，將粒子群算法用于伺服系統控制器參數自整定主要有以下優點：a）可同時對多項控制參數整定，比人工逐個調試各項參數的方法效率更高；b）可對大量控制參數自動進行計算，尋優范圍更廣，優化度更高；c）可根據實際需求自主設計算法的目標函數；d）可在指定范圍內進行參數尋優，使整定結果能夠保證系統的穩定性。

3 基于粒子群算法的伺服系統離線參數自尋優方法

本節結合電液伺服系統調試過程，分別確定粒子群算法的適應度函數、粒子編碼方式、參數搜索空間、粒子學習速度和算法規模，設計了一種基于粒子群算法的電液伺服系統離線參數自尋優方法。

3.1 適應度函數的設計

首先，根據控制系統任務書和人工調試結果確定尋優目標特性，即適應度函數。

對于同一伺服作動器，如果忽略泄露對其性能的影響，可以認為從伺服閥流量到作動器位移的傳遞特性GxQ不變，因此影響伺服系統性能的主要因素為控制偏差e到伺服閥流量Q的傳遞特性GQe。若能得到比較一致的傳遞特性GQe，即可保證伺服系統總體性能的一致性。由于伺服閥流量特性難以通過測量獲取，因此將傳遞特性GQe按照式（1）進行計算：

式中N為控制網絡的傳遞特性；Gxδ為指令信號到線位移的傳遞特性；Giδ為閥電流到線位移的傳遞特性。Gxδ和Giδ均可通過對測試數據進行分析獲得。

為得到穩定一致的GQe，則需Gxδ/GiδN在不同性能伺服閥條件下能夠保持一致。而對于固定的伺服閥和作動器，閥電流到作動器輸出線位移的傳遞特性通常保持不變，即Gxδ/Giδ頻率特性不變，且可通過對測試數據進行分析獲得。因此可以結合Gxδ/Giδ測試特性，計算得到需要的目標網絡特性N?，使Gxδ/GiδN特性保持一致。

使用粒子群算法對電液伺服系統進行整定時，需要建立單一的、能反映控制系統綜合性能的指標。本文以人工調試完成、性能較好的伺服系統的Gxδ/GiδN特性作為整定目標。參數尋優前，首先進行一次初測，得到待調試系統的閥電流到作動器輸出線位移的Gxδ/Giδ頻率特性，然后可通過計算解得所需要的控制網絡目標特性N?，將其作為適應度的計算準則。

粒子適應度的計算方法為：粒子當前位置值對應一組控制參數，計算按照該組控制參數設置的控制網絡頻率特性與目標網絡特性N?在各測試頻率點幅值特性的方差并求和取倒數。

適應度F的計算公式為

式中M0(ωi)為控制網絡目標頻率特性在第i個頻率點的幅值；P0(ωi)為控制網絡目標頻率特性在第i個頻率點的相位，共有m個頻率點；MN(ωi)為待評估的粒子位置代表的控制參數代入控制網絡時在相應頻率點的幅值；PN(ωi)為待評估的粒子位置代表的控制參數代入控制網絡時在相應頻率點的相位；ηM為幅值權值；ηP為相位權值。用粒子適應度描述粒子位置值對應的控制參數與能達到目標特性控制參數的接近程度，可以用該指標反映控制系統綜合性能。

3.2 粒子編碼方式和參數搜索空間

根據控制器可裝訂參數確定粒子編碼方式和參數搜索空間。伺服系統需要整定的控制參數包括控制器位置增益KP、積分增益KⅠ、陷波頻率w0、濾波器wf、濾波器阻尼ξ0及ξf，因此將粒子的解空間維數設為六維，位置編碼方式定義為［KP，KⅠ，w0，wf，ξ0，ξf］。為保證參數整定結果的穩定性，需要使粒子群在規定的控制參數范圍內進行整定。基于伺服系統穩定性分析結果和批產工藝數據包絡，確定參數尋優范圍為［0.7，1；0.2，0.25；100，200；0.01，1；100，200；0.01，1］。這是對電液伺服系統進行多次調試后總結出的控制參數范圍，并適當進行擴大，嘗試找到比歷史經驗更優的控制參數組合。

3.3 控制參數自整定方法

基于粒子群算法的電液伺服系統控制參數自整定具體步驟如下：

a）初始化粒子群信息。首先設置種群個數為200，迭代次數為100，慣性權重w為0.8，自我學習速度c1為0.5，群體學習速度c2為0.5。隨機產生各粒子的初始位置。

b）個體粒子有了初始位置后，計算每個粒子的適應度，適應度F按照式（2）進行計算。

c）分別記錄每個粒子的適應度，記錄每個粒子個體的歷史最佳位置xm和歷史最佳適應度fxm，并更新群體最佳位置ym和群體最佳適應度fym。

d）更新每個粒子的速度，其中，每個粒子速度的方向將朝著個體最優值和群體最優值的方向進行跟蹤，體現了粒子群算法的進化屬性，使得粒子群整體朝著全局最優點逐漸運動。粒子的速度更新公式為

式中 rand1，rand2為0～1之間的隨機值。

位置更新公式為

e）根據粒子更新后的位置，重復步驟b，計算新位置的適應度，并更新個體的歷史最佳位置xm、歷史最佳適應度fxm、群體最佳位置ym和群體最佳適應度fym。

f）達到最大迭代次數時，或多次運算后群體最佳適應度保持不變，或在搜尋到滿足要求的最佳位置時，終止計算。

基于粒子群算法的伺服系統控制參數自整定方法流程如圖2所示。

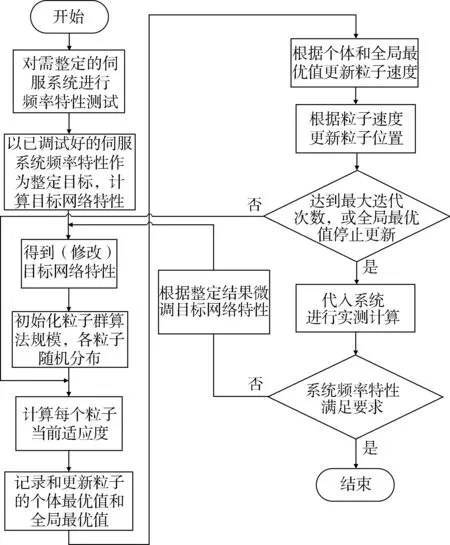
圖2 基于粒子群算法的伺服系統控制參數自整定流程Fig.2 Self-tuning process of servo system control parameters based on particle swarm optimization algorithm

4 整定實例

使用上述方法，對某電液伺服系統的一套伺服作動器進行參數自整定。

根據對該伺服作動器實測數據的分析，計算得到所需的控制網絡目標特性如圖3所示。

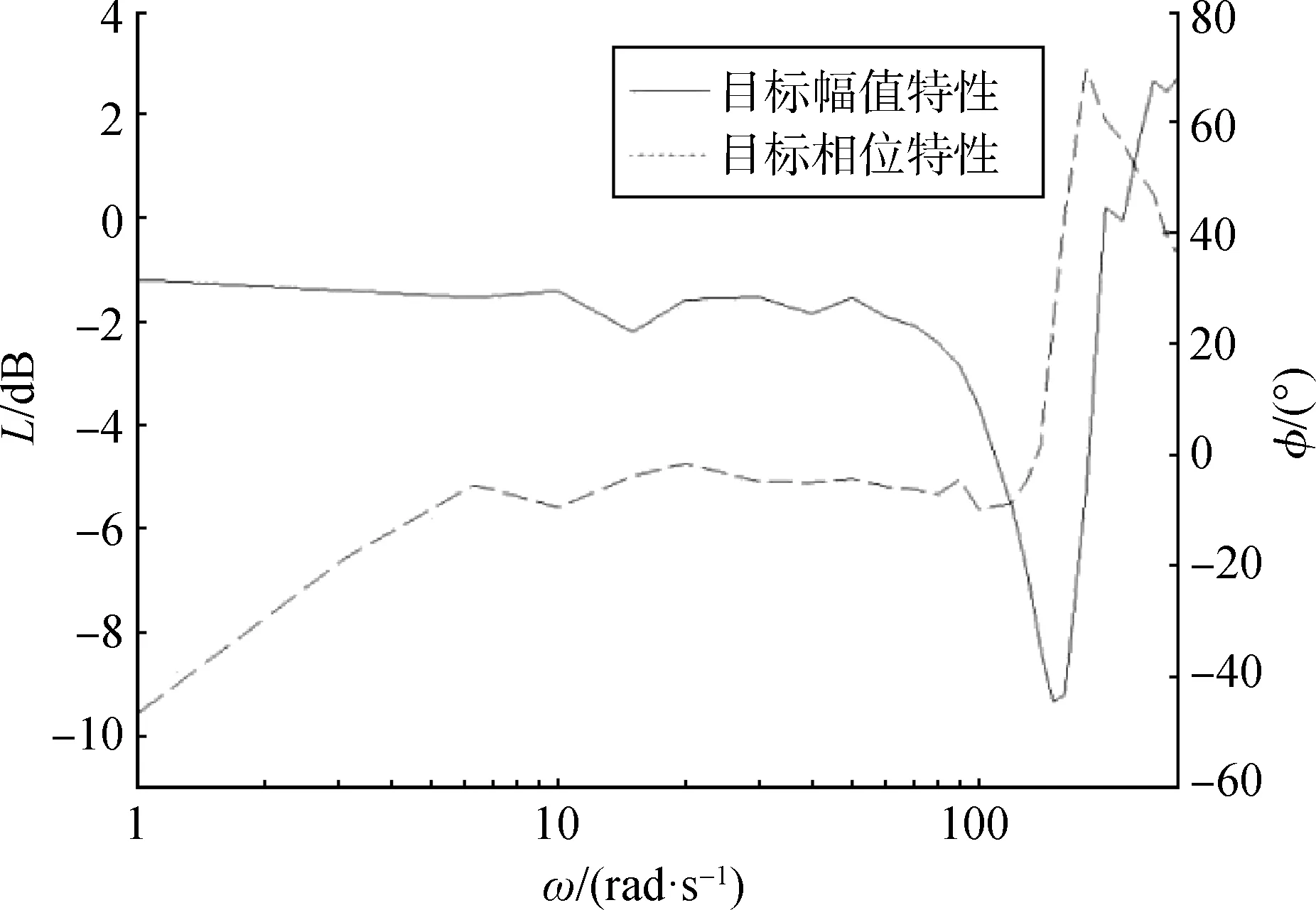
圖3 控制網絡目標特性Fig.3 Target characteristics of control network

運行粒子群算法，并改變運算規模進行多次仿真驗證，參數自整定結果如表1所示。

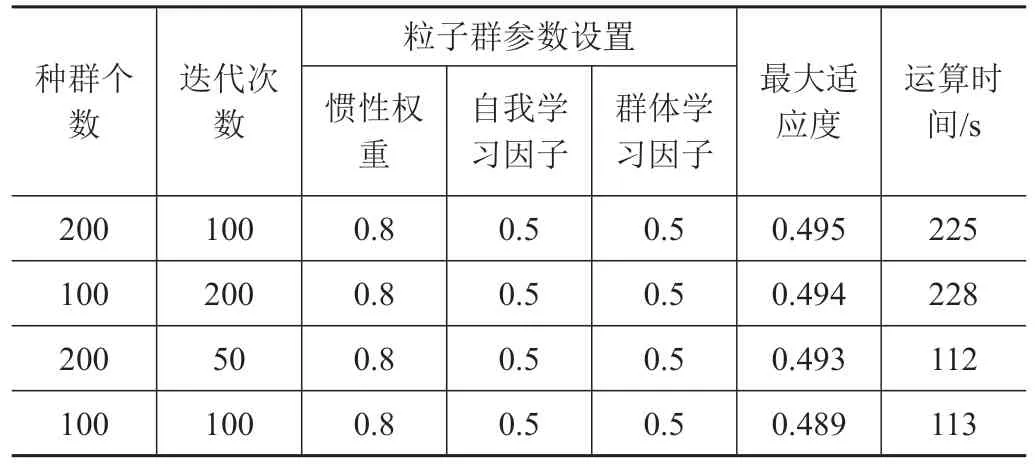
表1 粒子群算法參數自整定結果Tab.1 Parameter self tuning results of particle swarm optimization

由表1可知，基于粒子群算法的控制參數自整定方法可以在225 s 左右找到全局最優值。多次計算結果接近，證明該方法對初值選取具有一定的魯棒性，全局收斂性較好；且減小運算規模后，運算112 s 即已接近全局最優值，算法收斂較快。

適應度最大時的最優控制參數組合為KP=0.849，KⅠ=0.2，w0=158.047，ζ0=0.120，wf=194.413，ζf=0.311。

將粒子群算法求得的最優參數組合作為控制網絡的各項參數，控制網絡的頻率特性和目標網絡特性對比如圖4所示。

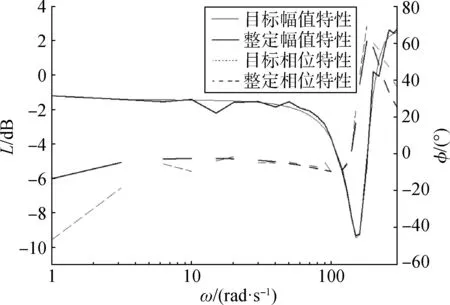
圖4 控制網絡的頻率特性和目標特性對比Fig.4 Comparison of frequency characteristics and target characteristics of control network

整定后伺服系統的閉環頻率特性如圖5所示。

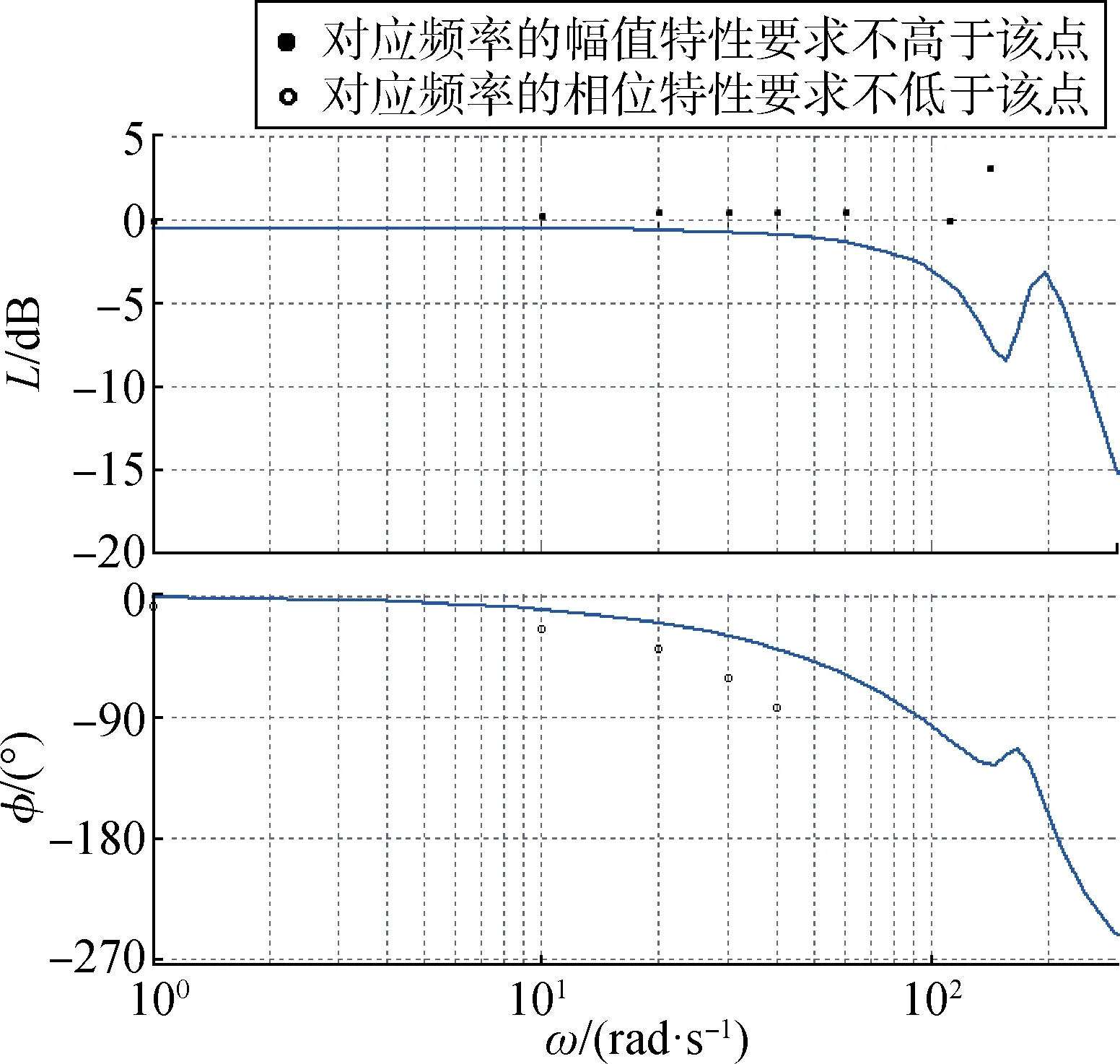
圖5 自整定后伺服系統的閉環頻率特性Fig.5 Closed loop frequency characteristics of servo system after self-tuning

由圖5可以看出，由粒子群算法整定后伺服系統的閉環頻率特性能夠滿足任務書要求，且余量充足。因此，通過基于粒子群算法的伺服系統控制參數自整定方法整定得到的控制參數組合可以對伺服閥的差異進行補償，使伺服閥性能具有差異的伺服系統傳遞特性GQe保持不變，在伺服閥小信號流量特性發生一定散布的情況下，保證伺服系統性能滿足任務書指標要求。

5 結束語

根據以上研究可知，將粒子群算法應用于對某電液伺服系統的控制參數自整定，可以實現數字伺服系統控制參數離線尋優的自動化。同時，使用粒子群算法得到的控制網絡頻率特性與能夠補償伺服閥特性散布的目標特性非常接近。仿真結果表明，該參數自尋優方法能同時對多項控制參數尋優，可大量節省人工調試時間，優化人工整定的繁瑣過程，具有更高的調試效率，能夠在保證系統穩定性的同時在更廣范圍內找到最符合實際需求的控制參數。