基于粗糙分析的大學英語考試質量提升路徑

柳媛慧,陳林書,趙肄江,彭理,梁偉

(湖南科技大學 1.外國語學院;2.計算機科學與工程學院,湖南 湘潭 411201)

在世界經濟、文化趨于一體化的形勢下,英語教育對大學生的重要性不言而喻,而檢驗大學英語教育教學質量和效果的最有效手段就是組織英語考試。大學英語考試是考查學生知識掌握情況、衡量教學效果、保證教學質量的重要手段,也是調整和改進教師教學工作,控制和激發學生學習行為的重要依據[1-2]。大學英語考試試題質量的高低直接影響考試的可靠度和準確度,進而直接或間接地影響學生的學習態度和學習行為。因此,提升大學英語考試試題質量是至關重要的一個研究課題。

傳統的大學英語考試試題質量提升路徑有數理統計法,即對試卷的平均分、標準差、可信度、覆蓋率、有效性、區分度以及優秀率、及格率和不及格率等指標進行統計和分析[3-5],進而對考試試題進行增刪調整和質量提升。其中:可信度衡量試題的可靠性與穩定性,覆蓋度表顯示知識覆蓋面的大小和程度,有效性表示考試實際結果與預期目標的差距,標準差反映分數的離散分布情況,區分度體現不同水平學生對同一類考試題的區分和鑒別能力。

然而,長期的大量實踐數據表明,上述傳統的數理統計方法僅能夠指導調整大學英語考試試題的難易程度、知識覆蓋面、有效性等,即只就卷面上的顯著問題進行簡單的統計、分析、評價和質量提升,不能深度挖掘試卷結構是否合理、試題內容與教學大綱是否一致,特別是不能智能判斷試題的冗余性(是否重復)、重要性程度(是否是教學重點)等信息[6]。

粗糙集理論[7]由波蘭數學家Pawlak提出,具有成熟的數學基礎,不需要先驗知識,避免了知識主觀評價帶來的誤差,其主要思想是在保持信息系統分類能力不變的前提下,通過知識約簡導出問題的分類或決策規則[8]。粗糙集理論是一種處理不精確、不一致、不完備信息的有效工具,直接對數據本身進行分析和推理,從中發現隱含的知識,揭示潛在的規律,它是一種天然的數據挖掘或者知識發現方法。粗糙集理論已廣泛應用于預測與控制、圖像處理、故障診斷、模式識別與分類、機器學習和數據挖掘等領域。

數理統計方法一般需要根據專家知識庫提供的主觀經驗值,如標準差、可信度和覆蓋率等統計指標,容易出現主觀評價帶來的誤差[9-10]。粗糙集理論正好能夠彌補數理統計方法的這一缺陷,它具有成熟的數學基礎,不需要任何主觀性的先驗知識,完全根據已有知識庫進行分析,挖掘潛在的隱含知識和規則,具有客觀性和價值性[11-13]。

本文借助粗糙集理論這一經典數學分析工具,研究大學英語考試質量提升路徑。下面借助粗糙集的決策表、相對正域、冗余屬性和屬性重要度基本概念,提出試題冗余性的定性判別方法和試題重要度的定量度量方法,建立基于粗糙分析的大學英語考試質量提升模型。大量實驗分析驗證了新方法的有效性,即新型方法發現并修正了部分冗余的和重要度較低的試題,有效提高了試卷命題質量,對指導大學英語教學工作、提高教學質量具有重要指導意義。

1 方法建模

本節先給出粗糙集中決策表和相對正域的形式化定義及其簡要描述,再根據粗糙集中相對正域和屬性重要性概念定義大學英語考試試題冗余性判別方法和試題重要度度量方法。

定義1(決策表)稱四元組K=(U,S,V,f)是一個信息系統或知識庫,簡單記為K=(U,S)。其中:論域U是對象的有限集合,屬性S是非空有限集合,屬性值域V=∪a∈AVa,Va表示屬性a∈A的值域,信息函數f:U×A→V是一個映射。進一步地,稱K為一個決策表,若滿足S中屬性,可劃分為兩個不相交的子集——條件屬性C和決策屬性D,其中,S=C∪D且C∩D≠φ,記為K=(U,C∪D)。特別地,稱K為一個單決策表,若滿足D=g0gggggg,記為K=(U,C∪g0gggggg)。

決策表是粗糙集理論中的一類特殊且非常重要的信息系統,多數決策問題在具體應用中都可以用決策表來解決。在實際應用中,通常用一張二維表表示信息系統。其中:行表示研究對象,列表示對象屬性,屬性值表示對象信息,一個或多個列屬性對應一個等價關系,一個二維表對應一族等價關系。

定義2(相對正域)給定決策表K=(U,C∪D),r?C,X?U則稱posC(D)為C相對于D的正域,其中,posC(D)如下:

(1)

相對正域posC(D)表示U中所有可以根據分類U/C的信息準確劃分到關系D的等價關系中去的對象集合。相對正域是粗糙集理論中一個非常重要的概念,它是屬性集C相對決策D的分類能力的強度描述。

1.1 試題冗余性判別方法

在大學英語考試中,可以將一個試題看作一個條件屬性r,將所有討論的目標試題看作條件屬性集C,并將所有目標試題的總分看作決策屬性D,那么,由目標試題和總分構成的成績表就是一個決策表,且是一個單決策表。于是,可以用如下方法定義試題冗余性。

定義3(試題冗余性)在給定決策表K=(U,C∪D)和試題r?C,若相對正域posC-{r}(D)=posC(D),則稱r為C相對D的不必要屬性,簡稱r為冗余屬性,否則稱r為C相對D的必要屬性。

上述定義中,給定大學英語考試試卷成績對應的決策表K=(U,C∪D)中,試題r?C,相對正域posC(D)表示試題集C相對總分D的分類能力描述。于是,我們可以用如下方法分析試題r是否冗余:若從試題集C中去掉試題r之后,剩余試題集C-{r}對決策D的分類能力沒有變化,則說明試題r是冗余的,是不必要的,是可以刪除的。

1.2 試題重要度度量方法

在大學英語考試試卷題型的成績表構成的決策表K=(U,C∪D)中,根據定義3試題冗余性的判別方法:若試題r是冗余屬性,則r的重要度為0,可以直接刪除,沒有繼續討論其試題重要度的意義了;否則,試題r是必要的。那么,接下來的問題是:試題r有多重要?如何對其進行定量、定義和度量呢?

于是,根據粗糙集理論中屬性重要度的概念,可以用如下方法定量度量試題r的重要度:試題r?C,根據定義1中相對正域posC(D)的概念,可以用兩個相對正域中元素個數之差來定量描述試題r的重要性程度,即利用定義4關于屬性重要度的計算公式來定量度量試題重要性。

定義4(試題重要度)給定大學英語考試試卷成績對應的決策表K=(U,C∪D),試題r∈C,則稱sig(r,C,D)為試題r相對于試題集C相對總分D的重要性程度,簡稱“r的試題重要度”。其中,|U|為學生集合U的基數,sig(r,C,D)如下:

(2)

上述定義中,若r是非必要的,則它的重要度顯然為0。但若屬性r是必要的,則可以用試題重要度來定量試題r的重要性。顯然,有sig(r,C,D)≥0,且:其值越大,r的重要度就越大;其值越小,r的重要度就越小。

2 實驗分析

首先,詳細交代實驗驅動、實驗目標、實驗數據離散化方法、實驗數據類型和實驗數據來源等內容;接著,以粗糙集的冗余屬性和屬性重要度為依據,提出大學生英語考試試題冗余性的定性判別方法;然后,給出大學生英語考試試題重要度的定量度量方法;最后,通過計算194名大學生的大學英語考試試題的冗余性和重要度,發現并修正了部分冗余的和重要度低的試題,有效提高了大學英語考試命題質量。

2.1 數據準備

大學英語考試試卷中,試題是基本元素,試卷的質量由所有試題的質量共同決定。整套試卷中,每一小題是否科學合理,是否滿足大綱要求,是否客觀反映學生的實際水平,對整套試卷的質量起著決定性作用。

在試卷中,有時會存在以下情況:兩道題目所考的內容相同或者相似,學生會做其中一道題,就會做另一道題,我們稱另一道題目是不必要的,冗余的,可以刪除的。有時還會存在另一種情況,且這種情況較常出現:某一題目比較容易,絕大多數學生都能夠回答正確,僅有極少數學生不能拿到分數,這說明這一試題重要度低,測試意義不大,應該對其進行替換或者難度調整。

但是,在考試之前,試題的冗余性和重要度很難由命題老師主觀給出,因為學生的基礎水平和學習情況參差不齊,命題老師既擔心考試題目太難導致學生考試不及格,又擔心考試太容易測試不出學生的真實水平。

本實驗不需要期望值和覆蓋標準等任何參考值。教師不在考試之前主觀評價或提升試卷質量,而是在考試之后通過學生考試成績反過來分析試題的冗余性和重要度,對冗余的或者重要度低的試題進行刪減和質量提升,從而提高試卷的整體質量。

在下面的實驗中,需要對大學英語考試的原始成績進行離散化處理。按照學校的一般性處理方法,將學生考試的百分制成績離散化為A(優秀,90～100分)、B(良好,80～89分)、C(中等,70～79分)、D(及格,60～69分)和E(不及格,60分以下)五個成績等級,如表1所示。

表1 百分制分數與離散后成績等級的對應關系

為便于分析題目的冗余性和重要度,需要進一步將每一道題目的得分離散化。例如:題目c1滿分為12分,某學生實際得分為8分,換算百分制為8÷12×100≈66.7分,則此學生題目c1的得分等級為D。按此方法,某學生的部分考試題目得分及離散化的成績等級如表1所示。其中:題目編號后括號內的數值表示該題目的總分數,如c1(8)表示題目c1的滿分為8分;“/”前后分別表示得分和對應的得分等級,如“8/A”表示題目c1得了8分,離散化的成績等級為A。

本次實驗的試卷樣本為湖南科技大學2021-22-2學期非英語專業大二英語期末考試試卷,考試題型有聽力題、閱讀理解題、翻譯題和寫作題(共55個題目計100分):Listening部分共23題計30分,其中題目1～16每題1分,題目17～23每題2分;Reading部分共30題計40分,其中題目24～33每題2分,題目34～53每題1分;Translation(Chinese to English)部分共1題計15分;Writing部分共1題計15分。題型構成如表2所示。

表2 大學英語考試試卷的題型構成

本次實驗的成績樣本為湖南科技大學2021級電子信息工程1～3班、能源化學工程2班、測控技術與儀器1班、車輛工程1班、機械電子工程1～2班、土木工程1～3班、工程管理2班共194名學生的考試原始成績,其中男生126人,女生68人。

2.2 實驗過程

下面根據定義3中試題冗余性判別方法分析樣本試題的冗余性。

為了讓討論簡單方便且不失一般性,隨機從試卷中抽取10名學生6道題目的考試分數作為樣本,試題原始成績如表3所示。再按表1中的方法離散化,得到對應分數等級的決策表,如表4所示。

表3 學生部分試題原始成績 (單位:分)

表4 學生部分試題原始成績離散化后的決策

將表4中的試題集{c1,c2,c3,c4,c5,c6}看作條件屬性C,總分看作決策屬性D,則表4是一個典型的決策表。利用定義3中冗余屬性的判別方法,可以分別判別試題{c1,c2,c3,c4,c5,c6}是否為不必要屬性,即是否是冗余的,可以刪除的。

根據表4容易求得決策屬性D、條件屬性集C和條件屬性集C-{c4}的等價類分別是:

再根據定義2,可分別求得條件屬性C和條件屬性C-{c4}相對決策屬性D的正域:posC(D)={2,4,5,6,7,8,9,10},posC-{c4}(D)={2,4,5,6,7,8,9,10}。

顯然,有posC-{c4}(D)=posC(D),則由定義3關于冗余屬性的判別方法可知,題目c4對總分D的分類能力不產生影響,是一個不必要屬性,是冗余的,可以刪除的。

同理,c6也是一個不必要屬性,是冗余的,可以刪除的。

但是,同理可求得,題目c1、c2、c3和c5是必要屬性,不可以刪除。

由上文可知,題目c4和c6是不必要屬性,說明對樣本學生1～10和樣本題目c1～c6來說,c4和c6對總分D的信息量劃分并沒有減少,即c4和c6是不必要的,是冗余的,可以刪除的,不太科學合理的。

下面根據定義4中試題重要度的判別方法分析樣本試題重要度。

為了讓討論簡單方便且不失一般性,隨機從樣本中抽取8名學生的Listening、Reading、Translation和Writing等4個題型的考試分數作為樣本,原始成績如表5所示。再按表1中的方法離散化,得到對應分數等級的決策表,如表6所示。

表5 學生各題型的原始成績 (單位:分)

表6 學生各題型原始成績離散化后的決策

根據表6容易求得決策屬性D(總分)、條件屬性集C和C-{Listening}的等價類分別是:

根據定義2,可分別求得條件屬性C和C-{Listening}的相對正域:

posC(D)={1,2,3,6,7,8},posC-{Listening}(D)={2,3,6,7,8}。

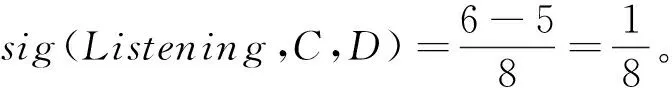
同理,可分別求得條件屬性Reading、Translation和Writing的屬性重要度:

從上述條件重要性的求解結果可知,顯然有sig(Reading,C,D)>sig(Writing,C,D)

>sig(Listening,C,D)=sig(Translation,C,D)。這說明,在大學英語考試中,Reading部分最重要,對總成績的影響最大,其重要度遠遠高于其他部分;其次是Writing部分;相比之下,聽力與翻譯的重要度最低。

2.3 結果分析

本次實驗的數據總量和計算工作量相當大。因此,實驗采用經典粗糙集數據分析工具集Rosetta 2.0,它具有數據導入、導出、補全、離散化、知識約簡、過濾、分類規則生成、等價類和上下近似集獲取等功能。實驗通過Rosetta 2.0軟件對194名大學生的成績進行了離散、等價類獲取、相對正域和屬性重要度求解等預處理和計算。

實驗需要將考生的試題離散化為A、B、C、D和E五個等級。但是,本次英語考試試卷的題目中1～33都是單項選擇題(即客觀題),要么是滿分(A級),要么是零分(E級),這意味著客觀題都是布爾類型數據,顯然不能將試題得分離散化為A、B、C、D和E五個等級。因此,需要在實驗中將多個單項選擇題組合成一個題目,如將選擇題1、2和3組合成題目c1。

在判別試題冗余性的實驗中,通過對194名大學生的42個組合題目進行統計分析,我們發現其中的兩組組合題目——題目3、11、30和題目19、27是冗余的,說明這些題目是不太科學合理的,需要對其進行修改和質量提升。

在定量度量試題重要度的實驗中,先對194名大學生的Listening、Reading、Translation和Writing共4個組合題目(題型)的試題重要度進行分析,得出的結論與2.2節的實驗結果基本一致,也與各題型的分值比例基本保持一致,其中,Reading、Listening、Writing和Translation部分的重要度占比分別為64.5%、24.8%、14.6%和14.1%,如圖1所示。這說明在大學英語考試命題中,應該將重點放在Reading部分,其次是Listening部分。相比較而言,Writing和Translation部分的重要性最低,且重要度基本相同,這與大學英語的教學目標和考試大綱是基本一致的。

圖1 試卷中各題型的重要性比例

接下來,繼續對194名大學生54個組合題目的試題重要度進行分析,我們發現,試卷所有題目的試題重要度基本呈正態分布,如圖2所示。共有28個題目的試題重要度在0.4～0.6之間,占全部54個題目的大多數;重要度在次高區間0.6～0.8和次低區間0.2～0.4的試題數量分別為8個和11個;重要度在最低區間0～0.2的試題只有6個;重要度在最高區間0.8～1.0的試題僅1個。我們可以對這些重要度比較低的題目進行修改和質量提升。從圖2可以看出,總的來話,英語試卷的試題重要度分布情況與命題預期目標基本一致,說明這份試卷內容主次分明,質量較高,基本符合教學大綱和考試大綱要求。

圖2 重要度區間的題目數量分布

3 結語

在已有研究[14-18]的基礎上,將粗糙集理論應用于大學英語考試命題,利用粗糙集相對正域、冗余屬性和屬性重要度等重要概念,提出試題冗余性定性判別方法,并提出試題重要度的定量度量方法,從而建立了基于粗糙分析的大學英語考試質量提升模型。實驗數據來源于參與湖南科技大學2021-22-2學期期末英語考試的大二非英語專業學生。實驗先對194名大學生42個組合題目的冗余性進行分析,發現2組組合題目是冗余的,說明這2組題目是不太科學合理的;再對194名大學生的4個題型和54個組合題目的重要度進行計算,發現所有試題的重要度基本呈正態分布,只有少數幾個題目的重要度較低。本研究結果能指導我們對少數冗余的或者重要度較低的考試題目進行修改和質量提升,有效提高了試卷的命題質量,對指導大學英語教學工作、提高大學英語教學質量具有重要指導意義。