結構阻尼比對超高層建筑順風向風振響應的影響

郭小飛 ,袁哲峰 ,王 瑞,牛方義

(1.中國建筑科學研究院有限公司,北京 100013;2.建研院檢測中心有限公司,北京 100013)

結構阻尼比是用來表示結構阻尼的大小,是用于結構在振動過程中能量耗散的基本術語[1]。阻尼比是超高層建筑結構風振響應分析中所要考慮的重要參數,直接決定著風荷載及風振系數的取值,進而會影響到超高層建筑結構的工程總造價。因此,論文研究阻尼比對超高層建筑結構的風振系數、基底剪力、加速度、位移等影響,為工程結構設計和規范的修正提供有效參考價值。限于篇幅,Davenport脈動風速譜對應的風荷載時程數據和工程概況參見論文《基于線性濾波法的超高層建筑脈動風速時程模擬》[2]。

1 風振系數分析方法

風荷載是高層建筑結構、高聳結構以及大跨度空間網殼結構設計時主要考慮的水平荷載之一。而在實際的抗風設計研究中,常常運用風振系數來表示。常用的風振系數分析方法有兩種形式,分別為荷載風振系數和位移風振系數。荷載風振系數為結構節點的靜力風荷載及脈動風荷載的總和與靜力風荷載的比值;位移風振系數為結構節點的靜力風荷載和脈動風荷載產生的位移總和與靜力風荷載產生的位移的比值[3]。采用規范[4]給出的荷載風振系數進行研究,公式為

(1)

式中,Fk(z)為順風向單位高度靜力風荷載(kN/m),可由式(2)得出。

Fk(z)=w0μsμz(z)B

(2)

式中,Fd(z)為順風向單位高度動力風荷載(kN/m),可由式(3)計算。

Fd(z)=m(z)(2πni)2φi(z)gσyi(z)

(3)

式中,m(z)為單位高度質量;ni為第i階頻率;φi(z)為第i階振型;g為峰值因子;σyi(z)為第i階振型z高度處的位移均方根。

我國規范對體型規則的建筑結構且其僅僅考慮一階振型,風振簡化計算公式為[4]

(4)

式中,ξ1為脈動增大系數;η1為脈動影響系數。

2 結構阻尼比對風振系數影響公式

結構阻尼比對建筑結構的影響作用主要體現在建筑結構的風致振動中,風振響應分析方法有頻域法和時域法。在實際的工程結構設計時,為使工程師能夠方便應用,我國《建筑結構荷載規范》(GB50009—2012)[4]采用等效靜力風荷載來計算結構的風致響應。下面將根據第一節介紹的內容對規范給出的風振系數公式進行推導,并詳細介紹阻尼比對風振系數的影響。

由式(3)可知,σq1為順風向一階廣義位移均方根,當假設相干函數與頻率沒有關系時,可由式(5)計算

(5)

將風振響應近似取為準靜態的背景分量及窄帶共振響應分量之和。則式(5)與頻率有關的積分項可近似表示為

(6)

而式(5)中與頻率無關的積分項乘以φ1(z)/μz(z)后以背景分量因子表示為

(7)

將式(2)、式(3)、式(5)～式(7)代入式(1),就可以得到我國《建筑荷載規范》[3]給出的風振系數計算表達式為

(8)

式中,脈動風荷載共振分量因子R可由式(9)計算。

(9)

式中,Sf為歸一化風速譜,采用Davenport教授建議的經典風速功率譜公式,則

(10)

由式(9)和式(10)就可以得到規范共振因子表達式

(11)

(12)

式中,f1為結構的第一階自振頻率(Hz);kw為地面粗糙度修正系數;ξ1為結構阻尼比。

由式(8)可以看出,阻尼比對風振系數的影響體現在共振風量因子上,并且阻尼比ξ1取值越小,風振系數公式中的共振響應因子R會越大,也就意味著風振系數βz越大,進而會導致計算風荷載越大。

3 阻尼比對風振系數的影響

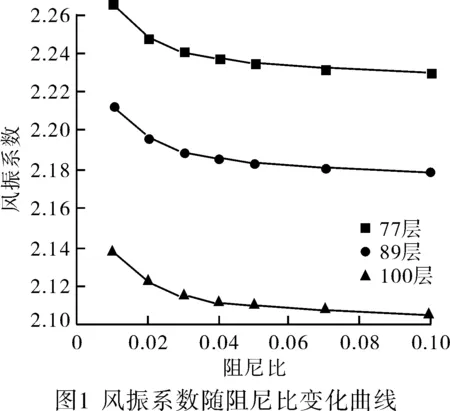
在進行超高層建筑結構風振響應分析過程中,阻尼比是一個不確定但又非常重要的因素。對于一般的鋼筋混凝土結構或鋼結構,阻尼比一般取值為0.01～0.05之間,為了精確地分析阻尼比對風振系數的影響,該文選擇阻尼比為0.01、0.02、0.03、0.04、0.05、0.07、0.1進行分析。圖1分別給出了第100層、第89層及第77層風振系數隨著結構阻尼比的變化規律曲線。由此可以看出,隨著阻尼比的增加荷載風振系數逐漸變小,并且變化規律漸漸趨于平緩,在結構阻尼比小于0.05時荷載風振系數緩慢變小,而在結構阻尼比大于0.05時荷載風振系數幾乎無變化,這說明阻尼比較大時對結構順風向的風振響應影響比較小。

4 阻尼比對基底剪力的影響

為了更好地了解阻尼比對建筑結構風荷載效應的影響,表1給出了不同阻尼比下結構的基底剪力最大值、平均值和均方根值。由此可以看出,整體上結構的基底剪力最大值、平均值和均方根值隨著阻尼比的增大而減小,且結構基底剪力最大值隨著阻尼比的增加減小幅度較大,而平均值和均方根值減小幅度較小,幾乎無變化。當阻尼比從0.01增加到0.02,基底剪力最大值減小了12.69%,均方根減小了0.80%。當阻尼比由0.02增加到0.03,基底剪力最大值減小了4.96%,均方根減小了0.30%。當阻尼比由0.03增加到0.04,基底剪力最大值減小了2.77%,均方根減小了0.12%。當阻尼比由0.04增加到0.05時,基底剪力最大值減小了1.45%,均方根減小了0.06%。當阻尼比由0.05增加到0.07時,基底剪力最大值減小了2.06%,均方根減小了0.06%。當阻尼比由0.07增加到0.1時,基底剪力最大值減小了1.70%,均方根減小了0.04%。

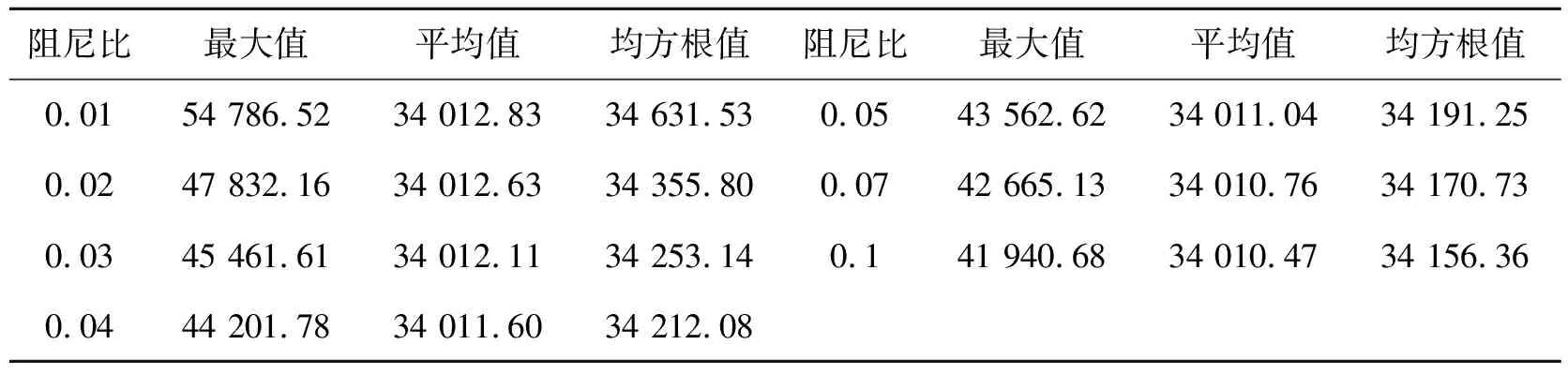
表1 不同阻尼比對基底剪力影響 /kN

5 阻尼比對位移的影響

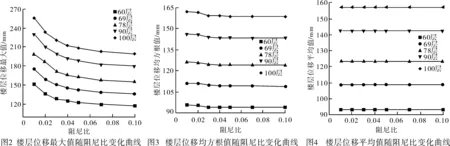
圖2給出了部分樓層位移最大值隨阻尼比的變化規律。圖3給出了部分樓層位移均方根值隨阻尼比的變化規律。圖4給出了部分樓層位移平均值隨阻尼比的變化規律。由圖可知,60層、69層、78層、90層和100層的樓層位移最大值、均方根值和平均值隨著阻尼比的變化規律基本一致,隨著阻尼比的增加樓層位移最大值減小幅度較大,而均方根值和平均值減小幅度較小,幾乎無太大變化,尤其是阻尼比大于0.03時。當阻尼比由0.01增加到0.02,100層的樓層位移最大值減小了8.73%,均方根值減小了0.28%。當阻尼比由0.02增加到0.03,100層的樓層位移最大值減小了5.80%,均方根值減小了1.37%。當阻尼比由0.03增加到0.04,100層的樓層位移最大值減小了3.31%,均方根值減小了0.19%。當阻尼比由0.04增加到0.05,100層的樓層位移最大值減小了2.16%,均方根值減小了0.09%。當阻尼比由0.05增加到0.07,100層的樓層位移最大值減小了2.54%,均方根值減小了0.09%。當阻尼比由0.07增加到0.1,100層的樓層位移最大值減小了1.82%,均方根值減小了0.06%。

6 阻尼比對加速度的影響

表2給出了頂層加速度最大值、最小值、平均值和均方根值隨阻尼比的變化規律。由此可知,隨著阻尼比的增大,頂層加速度最大值、最小值和均方根值變化量比較大,而平均值幾乎無變化。當阻尼比從0.01增加到0.02,頂層加速度最大值減小了33.85%,最小值增大了33.87%,均方根減小了15.36%。當阻尼比從0.02增加到0.03,頂層加速度最大值減小了21.06%,最小值增大了22.52%,均方根減小了28.17%。當阻尼比從0.03增加到0.04,頂層加速度最大值減小了15.72%,最小值增大了16.39%,均方根減小了13.34%。當阻尼比從0.04增加到0.05,頂層加速度最大值減小了12.02%,最小值增大了12.67%,均方根減小了10.38%。當阻尼比從0.05增加到0.07,頂層加速度最大值減小了8.48%,最小值增大了16.59%,均方根減小了15.08%。當阻尼比從0.07增加到0.1,頂層加速度最大值減小了8.51%,最小值增大了13.47%,均方根減小了15.73%。

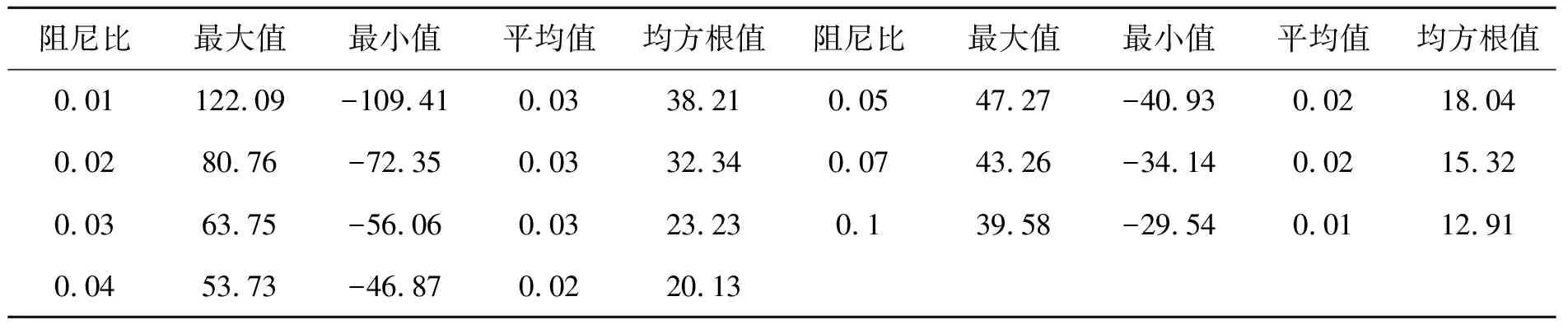
表2 阻尼比對頂層加速度的影響 /(mm·s-2)

7 結 語

阻尼比較大時對結構順風向的風振響應影響較小。隨著阻尼比的增加風振響應(基底剪力、樓層位移)最大值減小幅度較大,而均方根值和平均值減小幅度較小,幾乎無太大變化。隨著阻尼比的增加頂層加速度最大值、最小值和均方根值變化量比較大,而平均值幾乎無變化。