關于含參量不等式恒成立問題的試題探究
——以2023年新高考I卷第19題為例

湯一鳴 馬兆海 耿鳳杰

(中國地質大學(北京)數理學院 100083)

1 引言

含參量不等式恒成立問題是不等式、函數、方程等知識的交叉,對于這類新高考的熱點考題,學生在學習過程中難以形成固定的解題策略,遇到這一類問題時失分嚴重.不等式恒成立問題與函數最值聯系緊密,要求學生將化歸、分類討論、函數與方程等數學思想融會貫通,學會一題多解．本文以2023年新高考Ⅰ卷第19題為例談談該問題的解題教學策略．

2 追本溯源,真題呈現

已知函數f(x)=a(ex+a)-x.

(1)討論f(x)的單調性;

3 撥云見日,解法探究

(1)f′(x)=aex-1,當a≤0時,f′(x)<0在R上恒成立,f(x)在R上單調遞減;當a>0時,令f′(x)=0,得x=-lna,在(-∞,-lna)上f′(x)<0,在(-lna,+∞)上f′(x)>0.綜上所述,當a≤0時,f′(x)<0在R上恒成立,f(x)在R上單調遞減;當a>0時,f(x)在(-∞,-lna)上單調遞減,在(-lna,+∞)上單調遞增．

第(2)題給出了3種解法:

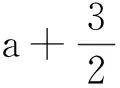
點評本題是一道典型的含參量不等式恒成立問題,但是它不具備進行參變量分離的條件,且其中給出的函數是非常規函數.注意到第一問求得f(x)的單調性,且不等式的右端不含自變量x,根據不等號的方向確定我們只需尋求f(x)的最小值,從而直接轉化成求解函數f(x)的最小值問題.對于此解法,由于復習備考中對恒成立問題已有訓練,因此學生容易想到利用導數思想求解函數相關問題,少數學生在問題轉化過程中出現邏輯混亂,錯誤地去求了函數的最大值．

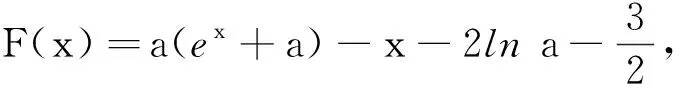
點評對于解決含參量不等式恒成立問題,移項構造函數不失為學生容易接受的方法之一,所以大部分學生能夠考慮到將原問題轉化為求解新構造函數的最值,使原問題迎刃而解.可是,運用這種方法的弊端在于,在中學數學知識范圍內,新構造的函數不一定能順利求得其最值,所以學生可以在嘗試該方法的基礎上判斷是否可行.對于此解法,部分學生得到新構造函數的最小值后發現形式不夠簡潔,并不能一眼看出正負,從而產生錯誤的心理暗示,無法繼續求解．

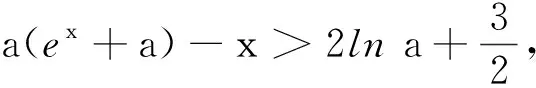
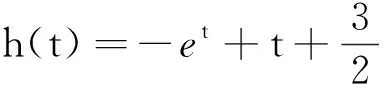
4 活學活用,變題訓練

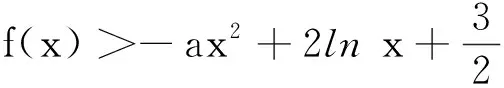
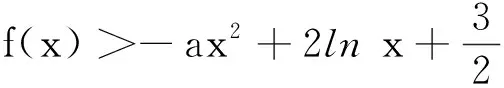
變題2已知函數f(x)=ex-a,證明:當a≤0時,f(x)≥e ln(ex+a).

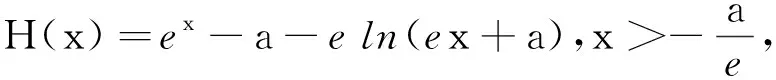
5 教學建議

(1)重視解題靈感與基本題型相結合

對學生而言,通過恒等變形構造函數及帶有隱零點的函數最值問題常常成為解決問題的“攔路虎”．真題解法3和變題2中,利用恒等變形的基礎是熟練運用指數與對數運算進行化簡,帶有隱零點的函數最值問題建立在用導數方法分析函數的最值之上．學生無法將這些基本題型遷移到待解決的問題上,解題思路就很難順暢．解題靈感來源于對高中數學基本題型解題方法的積累,教學環節一方面應注重對基礎知識的深度理解,培養學生的領悟力與獨立分析能力,另一方面建議以教材為基礎,以新高考試題為標桿,加強優質習題課建設,夯實基礎,將各部分知識系統化處理與融合,激發學生的學習熱情,推動由“雙基”到能力的升華．

(2)重視數學思想的本質教學

數學思想是數學學科本質的集中體現,是數學最為顯著的特征,是支撐全部數學大廈的脊梁,是數學知識發展的主線,是數學重要成就的提煉與反映[2]．轉化思想、分類討論思想和函數與方程思想在含參量不等式恒成立問題中的地位尤為顯著.學生總是將數學思想當作一種“方法”,形成做題的思維定式.比如在變題1中,學生容易陷入直接證明恒成立的“泥潭”,若換個角度思考,利用反證法,將恒成立作為條件,思路會柳暗花明．作為教師,應從數學思想角度切入教學,給予學生有價值的落腳點,充分發揮數學思想在育人層面上的抓手作用．因此,教學中應該摒棄一些邏輯思維跨度大、技巧性強的題目,避免給學生造成就題論題的困境,否則將不利于其深刻領悟其中蘊含的數學思想．教師在講授含參量不等式恒成立問題時,可以詳細解讀典型例題,注重凸顯不同例題中數學思想的本質區別,給學生時間去領會如何找到問題的突破口,以培養良好的數學思維品質．

(3)重視一題多解與一題多變

參變量分離法是學生解決含參量不等式恒成立問題的“法寶”．從真題角度上看,不是所有題目都能分離參變量,學生往往只知道方法本身而忽視了方法適用的條件．其實真題的解法多變,但考場上學生往往局限于一題一解,憑借自己的“經驗”解決問題,一旦思路阻斷就無法解題,因此課堂教學不是簡單解決問題的過程,還要教師注重一題多解的教學．高考試題具有穩中求變的特點,要求教師經過變題解題教學,幫助學生梳理變題中不變的思路與破題點,挖掘變題的創新之處,培養學生全方位思考的品質．