歷階而上:APOS理論下初中數(shù)學(xué)概念的階段教學(xué)與研究

何 蕾

(江蘇省蘇州外國(guó)語(yǔ)學(xué)校 214500)

1 問(wèn)渠哪得清如許——問(wèn)題提出,開(kāi)啟概念教學(xué)盲點(diǎn)

概念教學(xué)是數(shù)學(xué)教學(xué)的核心所在,國(guó)內(nèi)外專(zhuān)家從多學(xué)科角度,對(duì)數(shù)學(xué)概念教學(xué)提出了許多理論．斯根普(Skemp R．)認(rèn)為,事物的理解有兩種模式:工具性理解和關(guān)系性理解．盛興林指出,結(jié)構(gòu)主義理論探究了其在高中數(shù)學(xué)概念教學(xué)中的有效落實(shí)[1]．李彩虹和李祎基于APOS理論、多元表征理論及辨識(shí)教學(xué)理論整合了概念教學(xué)設(shè)計(jì)．自20世紀(jì)APOS理論創(chuàng)立以來(lái),基于該理論來(lái)研究數(shù)學(xué)概念教學(xué)的論文逐漸增多,呈上升趨勢(shì),是近幾年數(shù)學(xué)教學(xué)的熱點(diǎn)話題之一,該理論也成為概念教學(xué)的主流理論(圖1)．

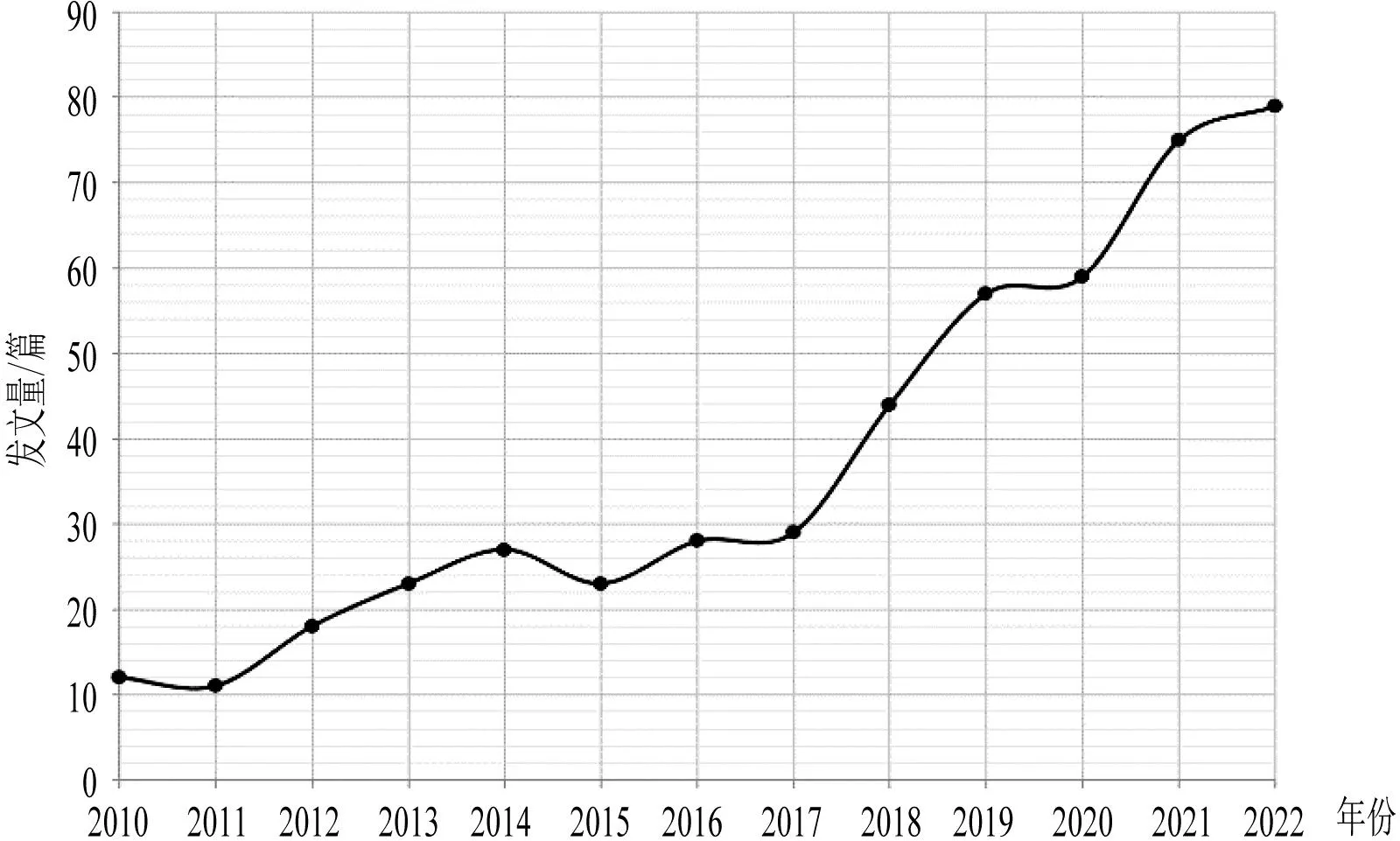
圖1 知網(wǎng)APOS概念教學(xué)主題發(fā)文趨勢(shì)圖

通過(guò)文獻(xiàn)梳理(圖2)發(fā)現(xiàn),目前關(guān)于數(shù)學(xué)概念教學(xué)的研究集中在具體到單一數(shù)學(xué)概念課教學(xué)設(shè)計(jì)的制定,而關(guān)于數(shù)學(xué)概念階段教學(xué)的研究不多．APOS理論的四個(gè)學(xué)習(xí)階段是合理的,揭示了學(xué)生學(xué)習(xí)數(shù)學(xué)概念的認(rèn)知心理和思維過(guò)程,這與當(dāng)前我國(guó)新課程所倡導(dǎo)的理念相一致,但對(duì)于章節(jié)階段教學(xué)、整體大單元階段教學(xué)如何深化概念教學(xué)沒(méi)有給出明確的策略．

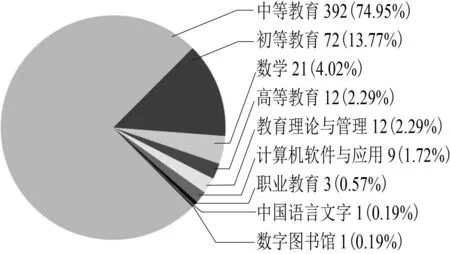
圖2 知網(wǎng)APOS概念教學(xué)主題學(xué)科分布

2 為有源頭活水來(lái)——APOS理論,支撐概念教學(xué)研究

美國(guó)數(shù)學(xué)家杜賓斯基等提出了APOS理論,四個(gè)字母分別表示理解數(shù)學(xué)概念的四個(gè)階段:活動(dòng)階段(Action),過(guò)程階段(Process),對(duì)象階段(Object),圖式階段(Schema)[2]．學(xué)生通過(guò)親身體驗(yàn)、直觀感知,觀察出一類(lèi)事物的共同特征,從而簡(jiǎn)潔并準(zhǔn)確地抽象出數(shù)學(xué)概念.經(jīng)過(guò)前三階段循序漸進(jìn)的學(xué)習(xí),此時(shí)的概念是學(xué)生認(rèn)知結(jié)構(gòu)中形成的包含實(shí)例、抽象過(guò)程、定義描述、類(lèi)比其他概念的核心圖式(圖3)．

圖3 APOS理論四階段模型

3 萬(wàn)紫千紅總是春——理論應(yīng)用,助力概念教學(xué)創(chuàng)新

APOS理論已經(jīng)廣泛應(yīng)用于函數(shù)、抽象代數(shù)、數(shù)論等多個(gè)高等數(shù)學(xué)領(lǐng)域．此理論指明了學(xué)生建構(gòu)數(shù)學(xué)概念的學(xué)習(xí)層次,同時(shí)為教師的數(shù)學(xué)概念教學(xué)提供了具體的教學(xué)策略．基于此理論,本文以概念教學(xué)所處三種不同階段為案例,搭好階段之“階”,歷階而上,對(duì)該理論下的概念教學(xué)進(jìn)行分析和研究,明確教學(xué)策略．

運(yùn)營(yíng)中心成立三年以來(lái),王棣實(shí)現(xiàn)了他的第一步戰(zhàn)略目標(biāo),就是成功把西王玉米胚芽油打造成為了中國(guó)玉米油第一品牌。

公元1世紀(jì),《九章算術(shù)》用文字描述的文辭代數(shù)階段,文字描述晦澀難懂.后來(lái)數(shù)學(xué)家開(kāi)始用字母或者符號(hào)來(lái)表示數(shù)量,標(biāo)志著縮略代數(shù)階段的到來(lái)．歐洲“代數(shù)學(xué)之父”韋達(dá),第一個(gè)系統(tǒng)地使用字母表示已知數(shù)、未知數(shù)及其乘冪,標(biāo)志著符號(hào)代數(shù)階段真正的開(kāi)始,為近世代數(shù)學(xué)的發(fā)展奠定了理論基礎(chǔ)．從具體數(shù)字到抽象符號(hào),是人類(lèi)對(duì)數(shù)的認(rèn)識(shí)的第一次大飛躍．

3.1 身臨情境,感悟文化美育,探求概念本質(zhì)

數(shù)學(xué)是美麗的．在教學(xué)實(shí)踐中,教師應(yīng)結(jié)合數(shù)學(xué)課程內(nèi)容,創(chuàng)新教學(xué)設(shè)計(jì),對(duì)學(xué)生進(jìn)行數(shù)學(xué)美的熏陶和教育,引導(dǎo)學(xué)生用數(shù)學(xué)眼光去欣賞世界．在生活情境中,用數(shù)學(xué)方法去理解世界,從而探求數(shù)學(xué)概念的本質(zhì)．以蘇科版九年級(jí)下冊(cè)第5章第5節(jié)“用二次函數(shù)解決問(wèn)題”為例．蘇州作為著名的江南水鄉(xiāng),橋梁建筑遍布,為學(xué)生提供了廣泛素材,使學(xué)生身臨其境,感悟姑蘇千年文化底蘊(yùn),從數(shù)學(xué)角度感悟蘇城之美,經(jīng)歷活動(dòng)之“階”．

·環(huán)節(jié)3 數(shù)形結(jié)合

通過(guò)幾何畫(huà)板實(shí)踐,將任意三角形繞任意一點(diǎn)旋轉(zhuǎn)任意角度即為旋轉(zhuǎn)的本質(zhì)意義．將旋轉(zhuǎn)任意角度變?yōu)樾D(zhuǎn)180°所成圖形就是中心對(duì)稱圖形;將任意一點(diǎn)移到三角形一邊中點(diǎn)旋轉(zhuǎn)180°,即得到平行四邊形;將任意三角形變?yōu)橹苯侨切?將一個(gè)直角三角形繞斜邊中點(diǎn),旋轉(zhuǎn)180°即得到矩形;一個(gè)等腰三角形繞斜邊中點(diǎn)旋轉(zhuǎn)180°即得到菱形;一個(gè)等腰直角三角形繞底邊中點(diǎn)旋轉(zhuǎn)180°即得到正方形．

師生共同尋訪古跡,欣賞了千年古建蘇州寶帶橋、新建的斜港大橋和石湖三岔橋．聞名中外的蘇州寶帶橋初建于中國(guó)唐朝,拱形近似于拋物線,是一座53孔石拱橋,如長(zhǎng)虹臥波,雄跨于大運(yùn)河之上.與之交相輝映的是2015年建成通車(chē)的斜港大橋(圖4)．石湖三岔橋又名雙曲拱橋,大跨低拱,結(jié)構(gòu)非常合理,看起來(lái)造型輕盈(圖5)．

圖4 蘇州寶帶橋和斜港大橋

問(wèn)題1千年古建蘇州寶帶橋、新建的斜港大橋和石湖三岔橋都是拋物線型的拱橋建筑.三座橋結(jié)構(gòu)造型差異較大,將它們的“橋拱”按照比例縮小后發(fā)現(xiàn),三橋拱形均形似拋物線．其中斜港大橋橋拱形狀與二次函數(shù)拋物線最為近似.那么在數(shù)據(jù)上有什么關(guān)聯(lián)呢?

·環(huán)節(jié)2 躍然紙上

活動(dòng)2在繪制美中建構(gòu)數(shù)學(xué)．

問(wèn)題2圖6為斜港大橋測(cè)繪圖.如果把斜港大橋拱形抽象成曲線AB,主橋?qū)挸橄蟪删€段AB,約為200 m,橋面到拱頂?shù)母呒s40 m,據(jù)此,如何準(zhǔn)確描述斜港大橋所呈現(xiàn)的這條拋物線?

天上的云靜靜地停那兒了。我摟著她，說(shuō)：“呦呦姐，我想我們都瘋了。”別呦呦說(shuō)：“人活著，就要瘋幾回，不然活著有什么勁呢？”

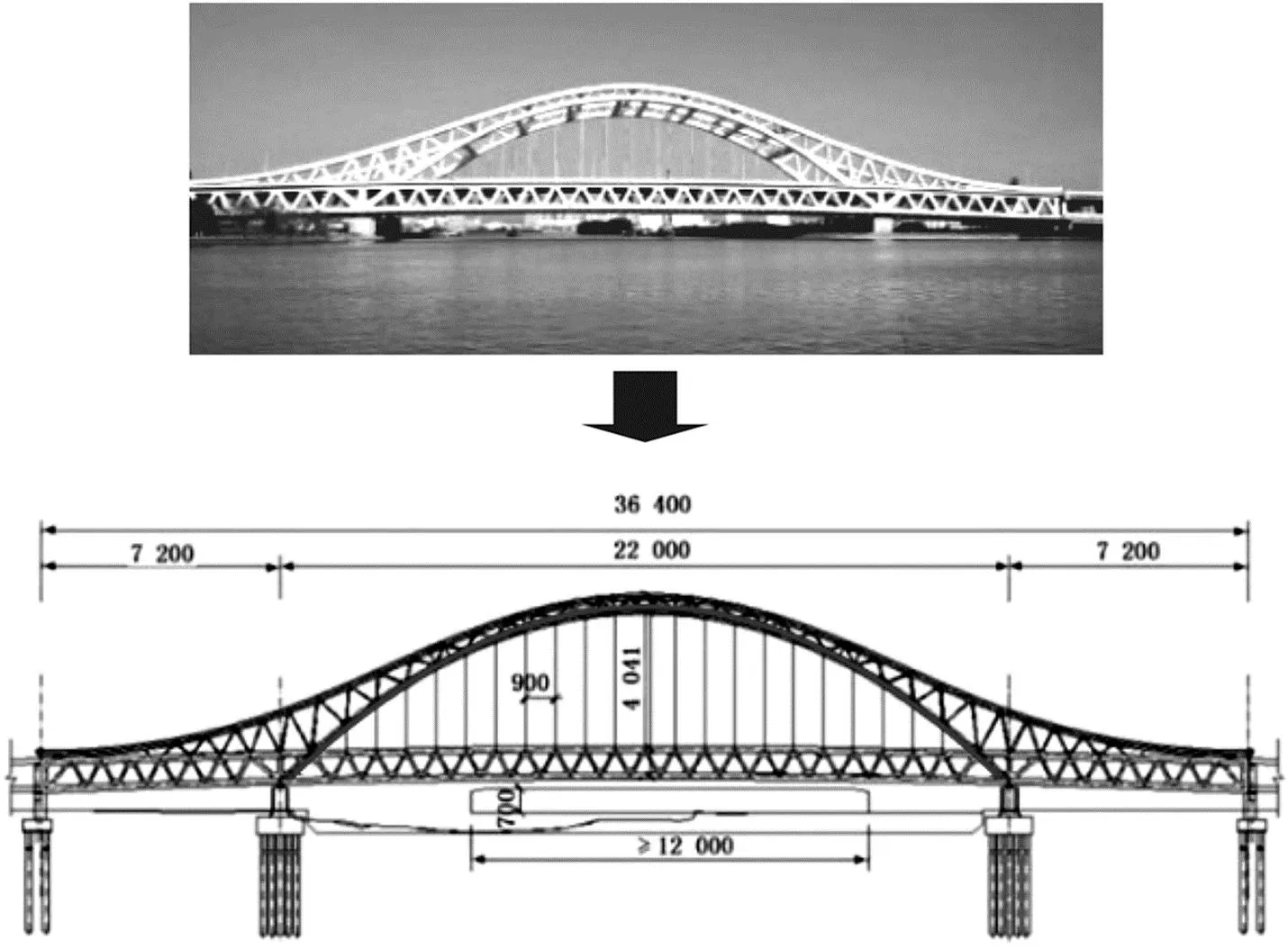
圖6 蘇州斜港大橋及測(cè)繪圖紙

·環(huán)節(jié)1 踏跡尋美

活動(dòng)3在計(jì)算美中探求本質(zhì)．

問(wèn)題3將實(shí)際問(wèn)題轉(zhuǎn)化為數(shù)學(xué)問(wèn)題,抽象出了曲線段AB,學(xué)生自由建立直角坐標(biāo)系,確定點(diǎn)A和點(diǎn)C的坐標(biāo),從而解得函數(shù)解析式,將另外一點(diǎn)B代入函數(shù)解析式,確定點(diǎn)B是否在經(jīng)過(guò)點(diǎn)A和點(diǎn)C的拋物線上.

學(xué)生通常采用表1中的四種形式建立平面直角坐標(biāo)系.選擇頂點(diǎn)位置不同,函數(shù)解析式也不同,但經(jīng)過(guò)運(yùn)算,點(diǎn)B在經(jīng)過(guò)點(diǎn)A和點(diǎn)C的拋物線上．從欣賞千年古建蘇州寶帶橋和新建的斜港大橋入手,讓學(xué)生直觀感受到了橋拱的拋物線形狀,經(jīng)過(guò)測(cè)繪、運(yùn)算等手段探尋了橋拱的本質(zhì),經(jīng)歷了過(guò)程之“階”．

表1 構(gòu)建函數(shù)模型

3.2 借助畫(huà)板,實(shí)現(xiàn)圖形直觀,構(gòu)建統(tǒng)一定義

(1)概念本質(zhì)之探究

數(shù)學(xué)是研究數(shù)量關(guān)系和空間形式的科學(xué)．圖形的平移、翻折、旋轉(zhuǎn)與位似是初中平面幾何學(xué)習(xí)內(nèi)容的四大重要變換,是研究特殊幾何圖形性質(zhì)和判定的重要方法．根據(jù)幾何圖形變換過(guò)程,培養(yǎng)學(xué)生想象出變換前后圖形的對(duì)應(yīng)變化．其中關(guān)鍵在于培養(yǎng)學(xué)生根據(jù)變換過(guò)程的語(yǔ)言描述刻畫(huà)出圖形,實(shí)現(xiàn)從幾何語(yǔ)言到圖形語(yǔ)言的跨越．發(fā)展學(xué)生推理能力和模型思想,讓學(xué)生根據(jù)圖形變換過(guò)程體悟、轉(zhuǎn)化、歸納,發(fā)現(xiàn)結(jié)論,證明結(jié)論．

(2)幾何畫(huà)板之協(xié)助

蘇科版教材八年級(jí)下冊(cè)第9章《中心對(duì)稱圖形》涉及大量幾何概念、特殊圖形性質(zhì)和判定:圖形的旋轉(zhuǎn),中心對(duì)稱與中心對(duì)稱圖形、平行四邊形、矩形等,概念間關(guān)聯(lián)薄弱,學(xué)生學(xué)習(xí)每個(gè)概念時(shí)都需要重新建構(gòu)、辨析概念．教學(xué)中需要思考如何去突破概念間的束縛,化歸為同一類(lèi)文字語(yǔ)言,探究特殊幾何圖形動(dòng)態(tài)形成的本質(zhì),形成本章節(jié)中心對(duì)稱圖形概念的統(tǒng)一定義．

本章節(jié)以旋轉(zhuǎn)為基礎(chǔ)概念,課本定義是“將一個(gè)圖形繞一個(gè)定點(diǎn)轉(zhuǎn)動(dòng)一定的角度,這樣的圖形運(yùn)動(dòng)叫作圖形的旋轉(zhuǎn)”．借助幾何畫(huà)板,從旋轉(zhuǎn)中心、旋轉(zhuǎn)方向和旋轉(zhuǎn)角這三個(gè)基本要素出發(fā),對(duì)圖形變換進(jìn)行研究,發(fā)現(xiàn)幾何圖形概念在幾何原理、文字描述兩方面都具備一致性,得出一般思想、一般結(jié)論．

(3)追本溯源之新論

長(zhǎng)期疾病相關(guān)心理問(wèn)題是影響糖尿病治療的另一重要因素。調(diào)查研究顯示，糖尿病18個(gè)月的相關(guān)心理痛苦的發(fā)生率為38%～48%，在不同程度上影響糖尿病患者的治療依從性、自我管理行為、血糖控制[8]。且針對(duì)住院的糖尿病患者的研究表明[2]，糖尿病新住院患者普遍存在不同程度的心理痛苦，患者的回避應(yīng)對(duì)和屈服應(yīng)對(duì)水平越高，心理痛苦程度越大。因此，可以從健康教育著手，提高患者對(duì)疾病的認(rèn)識(shí)，消除不必要的恐懼和排斥，讓患者以正性的態(tài)度對(duì)待糖尿病，減輕心理痛苦，自然能改善治療效果。

隨著我國(guó)企業(yè)的改革和創(chuàng)新的不斷推進(jìn)，公司的治理結(jié)構(gòu)也不斷優(yōu)化，要想從財(cái)務(wù)治理結(jié)構(gòu)透視財(cái)務(wù)管理目標(biāo)。還需要積極轉(zhuǎn)變企業(yè)的經(jīng)營(yíng)管理理念，在治理結(jié)構(gòu)的優(yōu)化過(guò)程中進(jìn)一步提高對(duì)財(cái)務(wù)管理目標(biāo)的關(guān)注，首先，企業(yè)的管理層要積極明確企業(yè)財(cái)務(wù)管理的重要性，并緊隨公司治理結(jié)構(gòu)的調(diào)整，制定明確的財(cái)務(wù)管理目標(biāo)，為財(cái)務(wù)管理工作的實(shí)施提供的導(dǎo)向。其次，也要積極加大對(duì)財(cái)務(wù)管理的關(guān)注。積極健全和優(yōu)化企業(yè)的財(cái)務(wù)管理制度。協(xié)同企業(yè)的治理結(jié)構(gòu)，切實(shí)保證企業(yè)財(cái)務(wù)管理工作和企業(yè)改革的有序開(kāi)展。

活動(dòng)1在欣賞美中提出問(wèn)題．

·表達(dá)之根——代數(shù)式

表2 中心對(duì)稱圖形的統(tǒng)一定義

3.3 尋根究底,完整框圖結(jié)構(gòu),深化體系發(fā)展

(1)開(kāi)啟尋根之旅

需要展示的氣象要素包括規(guī)則格點(diǎn)和離散站點(diǎn)兩大類(lèi)。規(guī)則格點(diǎn)資料原始數(shù)據(jù)形式由Micaps4類(lèi)或13類(lèi)等二維網(wǎng)格表示形式和Micaps2類(lèi)的站點(diǎn)列表表示形式,Micaps4類(lèi)或13類(lèi)格式數(shù)據(jù)用自適應(yīng)網(wǎng)格數(shù)據(jù)提取技術(shù),根據(jù)顯示比例和展示的樣式尺寸自動(dòng)計(jì)算出適合展示的網(wǎng)格密度,隨著地圖縮放自動(dòng)調(diào)整。Micaps2類(lèi)格式數(shù)據(jù)通過(guò)對(duì)各點(diǎn)坐標(biāo)的分析計(jì)算出網(wǎng)格參數(shù)后轉(zhuǎn)換成網(wǎng)格形式再進(jìn)行后續(xù)處理。離散站點(diǎn)由于站點(diǎn)密度分布不規(guī)則,無(wú)法采用規(guī)則格點(diǎn)方式自動(dòng)計(jì)算,本平臺(tái)采用分級(jí)展示技術(shù),根據(jù)站點(diǎn)級(jí)別/重要性等將站點(diǎn)分組,隨著縮放比例自動(dòng)確定顯示哪些組,確保內(nèi)容顯示完整性和版面的可讀性。

數(shù)學(xué)新概念的學(xué)習(xí),就是一場(chǎng)尋根之旅和創(chuàng)新之旅的完美二重奏．“新概念”“新定義”題型是熱門(mén)話題,需要重視新知識(shí)的“根”,找到了根也就找到了新知識(shí)的生長(zhǎng)點(diǎn)和延伸點(diǎn)．學(xué)生感悟到了新數(shù)學(xué)概念產(chǎn)生的必要性,才能激發(fā)學(xué)習(xí)數(shù)學(xué)新概念的思維需求[3]．初中代數(shù)主要包含數(shù)、代數(shù)式、方程和函數(shù)四大部分,各部分之間存在聯(lián)系,教學(xué)實(shí)施中應(yīng)幫助學(xué)生構(gòu)建完整的代數(shù)框圖結(jié)構(gòu)．

·學(xué)科之根——數(shù)

數(shù)是數(shù)學(xué)學(xué)科的基石,是人類(lèi)在生產(chǎn)生活中從具體事物中抽象出來(lái)的．古時(shí)候的結(jié)繩計(jì)數(shù),就是最初的數(shù)字抽象概念．客觀上存在意義相反的兩種量,當(dāng)被減數(shù)小于減數(shù)時(shí),負(fù)數(shù)就產(chǎn)生了．隨著運(yùn)算法則的發(fā)展,出現(xiàn)了加、減、乘、除四則運(yùn)算以外的乘方和開(kāi)方運(yùn)算,產(chǎn)生了無(wú)理數(shù),至此完成了初中階段實(shí)數(shù)范圍的數(shù)系擴(kuò)充．

將旋轉(zhuǎn)作為圖形的一般變換方法,僅對(duì)旋轉(zhuǎn)對(duì)象層層深入,即可實(shí)現(xiàn)中心對(duì)稱圖形的層層遞進(jìn),完成中心對(duì)稱圖形統(tǒng)一定義的華麗蛻變．所呈現(xiàn)的概念性質(zhì)顯明,原理一致,闡明了系列中心對(duì)稱圖形新的統(tǒng)一定義,經(jīng)歷了對(duì)象之“階”(表2)．

③磨礦分級(jí)流程交叉影響，旋流器分級(jí)效率低，溢流濃度低，進(jìn)而使球磨機(jī)循環(huán)負(fù)荷重，磨礦效率低。一段弱磁選及強(qiáng)磁選混合精礦濃度很低，使得一段旋流器的分級(jí)效率很低，在20%以下，一段旋流器溢流濃度僅2%；一段旋流器的分級(jí)效率很低使得二段磨球磨機(jī)負(fù)荷重，磨礦效率低，二段旋流器與磨機(jī)匹配性不好，分級(jí)效率不高，溢流細(xì)度-0.043 mm粒級(jí)含量?jī)H在65%左右；

·建模之根——方程

需求計(jì)劃提報(bào)不嚴(yán)謹(jǐn)，隨意性較大，隨意變更時(shí)間或數(shù)量，從而導(dǎo)致部分材料數(shù)量過(guò)高與部分材料短缺同時(shí)發(fā)生，庫(kù)存積壓與短缺同時(shí)存在，成本上升但卻效率低下。設(shè)計(jì)變更多，實(shí)際工作中，設(shè)計(jì)變更是常態(tài)，而此時(shí)如果采購(gòu)已經(jīng)完成，勢(shì)必造成積壓。現(xiàn)狀表明：因計(jì)劃調(diào)整、設(shè)計(jì)變更、工程剩余等需求計(jì)劃不準(zhǔn)確是造成企業(yè)物資積壓的主要原因。

一般情況下，我們都是在兩個(gè)層面上談?wù)摵诵乃仞B(yǎng)問(wèn)題的.一是一般意義的層面，二是學(xué)科意義的層面.本文討論的話題主要是建立在數(shù)學(xué)學(xué)科意義層面上的，即基于學(xué)科意義下的數(shù)學(xué)素養(yǎng)的培養(yǎng)路徑問(wèn)題.

在解決實(shí)際問(wèn)題需要比較兩個(gè)代數(shù)式關(guān)系時(shí),產(chǎn)生了相等和不等兩種情況．有條件相等就是方程式,無(wú)條件相等就是恒等式．方程可以類(lèi)比代數(shù)式的分類(lèi),分為有理方程和無(wú)理方程．同樣類(lèi)比代數(shù)式的分類(lèi),有理方程可以分為整式方程和分式方程．對(duì)解方程的探究歷經(jīng)千年,“負(fù)數(shù)”和“虛數(shù)”這兩個(gè)怪物的出現(xiàn),嚴(yán)重影響了方程體系和解方程的發(fā)展之路．

漏電保護(hù)器的裝設(shè)場(chǎng)所；由于人手握住手持式或移動(dòng)式電器時(shí)，如果該電器漏電，則人手因觸電痙攣而很難擺脫，觸電時(shí)間一長(zhǎng)，就會(huì)導(dǎo)致死亡，而固定式電器漏電，如人體觸及，會(huì)因電擊刺痛而彈離，一般不會(huì)繼續(xù)觸電.由此可見(jiàn)，手持式和移動(dòng)式電器觸電的危險(xiǎn)性遠(yuǎn)大于固定式電器觸電，因此一般規(guī)定，安裝手持式和移動(dòng)式電器的回路上應(yīng)裝設(shè) RCD.由于插座主要是用來(lái)連接手持式和移動(dòng)式電器的，因此插座式回路上也應(yīng)裝設(shè)RCD.GB50096-1999 《住宅設(shè)計(jì)規(guī)范》規(guī)定，除空調(diào)機(jī)電源插座外，其它電源插座回路均應(yīng)裝設(shè)RCD.

·預(yù)測(cè)之根——函數(shù)

利用二元一次方程表示兩個(gè)變量之間的對(duì)應(yīng)關(guān)系,這就是最初的函數(shù)意識(shí)．當(dāng)其中一個(gè)變量隨著另一個(gè)變量的變化而變化,形成了最樸素的函數(shù)概念．從常數(shù)到變數(shù),是人類(lèi)對(duì)數(shù)的認(rèn)識(shí)的第二次大飛躍．用代數(shù)式中的字母表示變數(shù),那么這個(gè)式子就是代數(shù)函數(shù)．初中主要研究一次(二次)函數(shù),這兩個(gè)函數(shù)和二元一次(二次)方程有著密切的聯(lián)系,本質(zhì)就是等量關(guān)系．

(2)顯現(xiàn)圖式之根——大單元框圖結(jié)構(gòu)

[36] “Limits in the seas-No.143 China’s Maritime Claims in the South China Sea”, Office of Ocean and Polar Affairs, Bureau of Oceans and International Environmental and Scientific Affairs, U.S. Department of State, December 5, 2014.

從數(shù)到代數(shù)式,再到方程和函數(shù),應(yīng)用導(dǎo)圖視角,構(gòu)建完整的數(shù)學(xué)概念網(wǎng)絡(luò)系統(tǒng),明確每個(gè)知識(shí)的“根”,幫助學(xué)生形成組織良好的概念網(wǎng)絡(luò)結(jié)構(gòu)．引導(dǎo)學(xué)生完成代數(shù)知識(shí)結(jié)構(gòu)體系構(gòu)建,旨在形成組織良好的數(shù)學(xué)認(rèn)知結(jié)構(gòu)網(wǎng)絡(luò);促進(jìn)學(xué)生對(duì)新概念的思考和理解,重視學(xué)生對(duì)所學(xué)概念的梳理歸納、改造重組和系統(tǒng)提升.一段時(shí)間教學(xué)后,需要適時(shí)幫助學(xué)生完善知識(shí)結(jié)構(gòu)框圖(圖7),陪伴學(xué)生完整經(jīng)歷圖示之“階”．

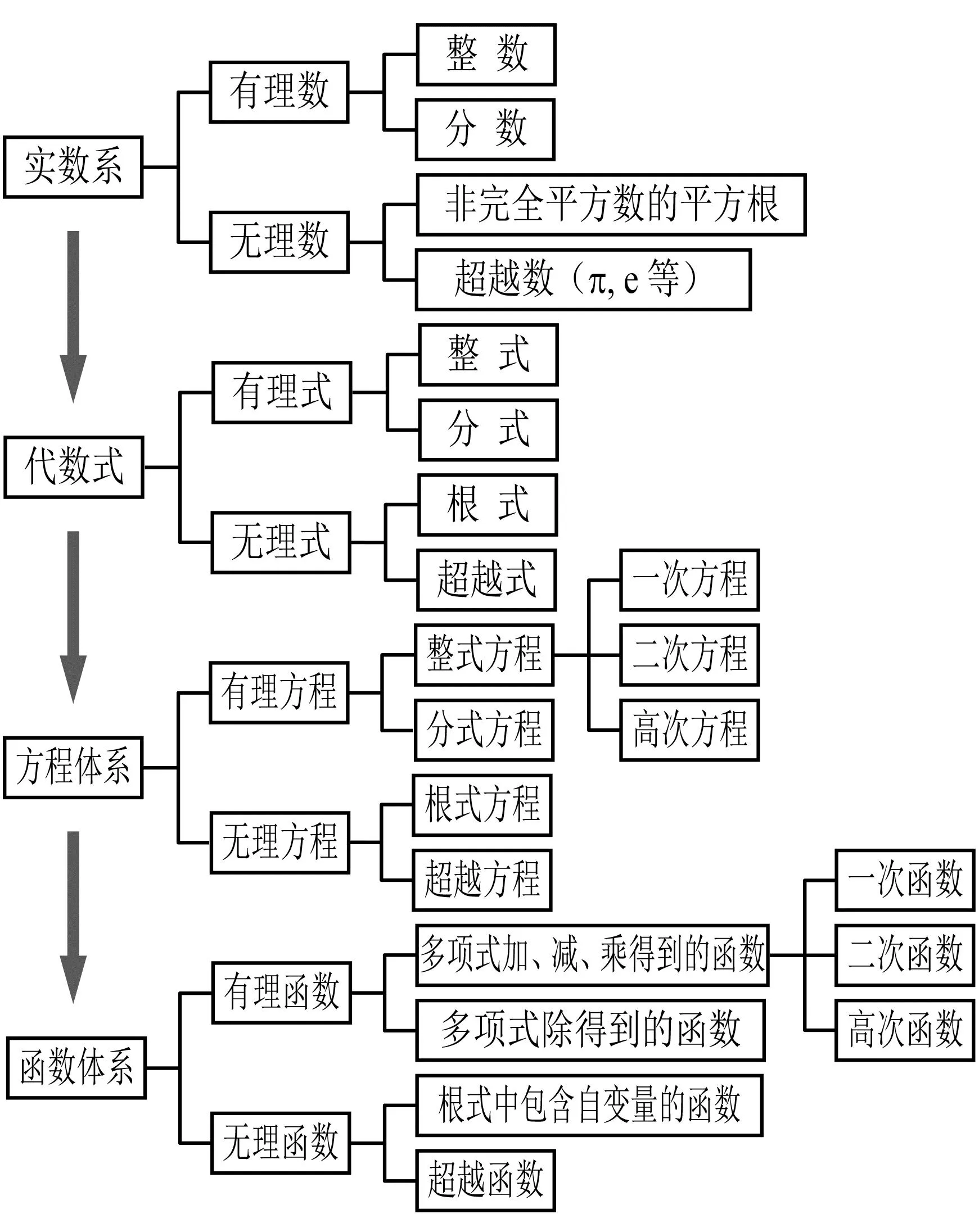
圖7 初中數(shù)學(xué)代數(shù)四大部分結(jié)構(gòu)框圖

4 結(jié)束語(yǔ)

概念教學(xué)是數(shù)學(xué)教學(xué)的基礎(chǔ)和核心,讓學(xué)生身臨其境,直觀感悟數(shù)學(xué)概念,有助于啟發(fā)學(xué)生的深度思維、強(qiáng)化數(shù)學(xué)概念．教師在教學(xué)中要善于歸納概念的本質(zhì)和研究方法,形成組織良好的數(shù)學(xué)概念認(rèn)知結(jié)構(gòu)網(wǎng)絡(luò)和圖式．在概念教學(xué)中經(jīng)歷活動(dòng)之“階”、過(guò)程之“階”、對(duì)象之“階”、圖示之“階”．歷階而上,從概念課教學(xué)設(shè)計(jì)入手,擴(kuò)展到階段章節(jié)概念教學(xué),直至完成初中階段代數(shù)整體大單元的概念教學(xué)．概念不是某節(jié)新課的專(zhuān)利,概念教學(xué)需要教師有大局觀、整體觀,有意識(shí)地進(jìn)行階段性歸納與反思,最終實(shí)現(xiàn)三級(jí)階梯式的完美進(jìn)階．