輪轂式電動汽車電子差速復合控制方法

陳和娟，涂宏慶，路 露

（1.無錫商業職業技術學院，江蘇 無錫 214153；2.南京工程學院，江蘇 南京 211167）

1 引言

輪轂式電動汽車采用輪轂電機技術，將電機獨立安裝在車輪內，與傳統發動機驅動或單電機驅動方式的汽車相比較，減少了差速器和減速器等部件，具備機械結構簡單、控制更加靈活、底盤結構更加簡化等優勢，成為汽車行業研究熱點和發展趨勢［1-3］。

電子差速控制技術指的是采用合適控制算法獨立控制驅動輪的轉速或轉矩，以實現汽車在彎道路徑或者復雜工況導致內外驅動輪速度以及受力不一致情況下的行駛安全性及穩定性。該項技術作為輪轂電機技術的關鍵，近年來隨著電動汽車的推廣受到國內外學者的廣泛研究，歸納起來可分為三類：（1）基于轉速的差速控制，主要是借助Ackermann轉向模型獲取各驅動輪的目標轉速，并采用控制算法使驅動輪轉速跟蹤目標轉速，文獻［4］根據Ackermann轉向模型獲取四輪驅動電動車的四個驅動輪的轉速關系，并設計一種PID控制器，實現了差速轉向；文獻［5］則建立了車輛神經網絡模型，獲取了驅動輪轉速與車輛車速及轉角之間的非線性關系，進而實現差速控制。此類方法由于Ackermann模型未考慮高速時的車輛橫擺，因此主要適用于低速狀態下的差速控制。（2）基于轉矩的差速控制，車輛在彎道行駛時，內外車車輪的轉速不同導致控制內外輪的轉矩也不相同，因此可以通過獨立控制內外側車輪的轉矩實現電子差速，文獻［6］應用BP神經網絡理論設計了一種基于轉矩的電子差速控制策略，并通過仿真驗證了該控制方法能夠較好地解決電動輪汽車的電子差速問題；文獻［7］建立了汽車電子差速控制模型，并提出一種模糊控制方法，對車輪進行獨立的轉矩控制，實現差速控制。此類方法需獲得精確的理論轉矩，對車輛建模的精準度要求較高。（3）基于滑移率的差速控制，主要是針對理想轉矩獲取困難的問題，通過將各驅動輪滑轉率控制在理想目標區域內，對驅動輪轉矩進行分配，從而實現差速控制。文獻［8］構建了車輛的三自由度整車模型，并基于最優控制和滑模控制理論，提出一種相對滑移率最優控制器，實現了在彎道路徑行駛時車輛相對滑移率最小；文獻［9］同樣針對車輛驅動輪的相對滑移率控制問題，設計了一種雙閉環控制系統，實現了系統的差速控制。此類方法較難滿足一些復雜行駛工況，與前兩類方法一樣均具有一定局限性。

這里針對上述所提單類控制方法的局限性，以前輪轉向后輪驅動的輪轂式電動汽車為研究對象，提出了一種基于轉速和滑移率的復合電子差速控制方法，當汽車處于低速行駛狀態時，根據Ackermann轉向模型獲取驅動輪期望轉速，采用模糊PID控制方法，實現對期望轉速的跟蹤控制；當汽車處于高速行駛狀態時，構建汽車三自由度模型，以驅動輪的相對滑移率作為反饋控制量，提出一種基于模糊逼近的優化控制方法，在保證汽車行駛穩定性的同時，實現了彎道行駛驅動輪相對滑移率最小，且無需建立精確的狀態空間模型，大大減小了計算量。仿真實驗證明，這里提出的高-低速復合控制策略能夠使汽車在不同行駛速度下實現穩定轉向。

2 汽車建模

2.1 汽車Ackermann轉向模型

當汽車在彎道低速行駛時，可把其四個車輪看作是圍繞某個圓心做圓周運動，如圖1所示。假設汽車為一剛體，則其滿足Ackerman 轉向模型［10］，并可由此獲得轉向車速與之間的運動學關系：

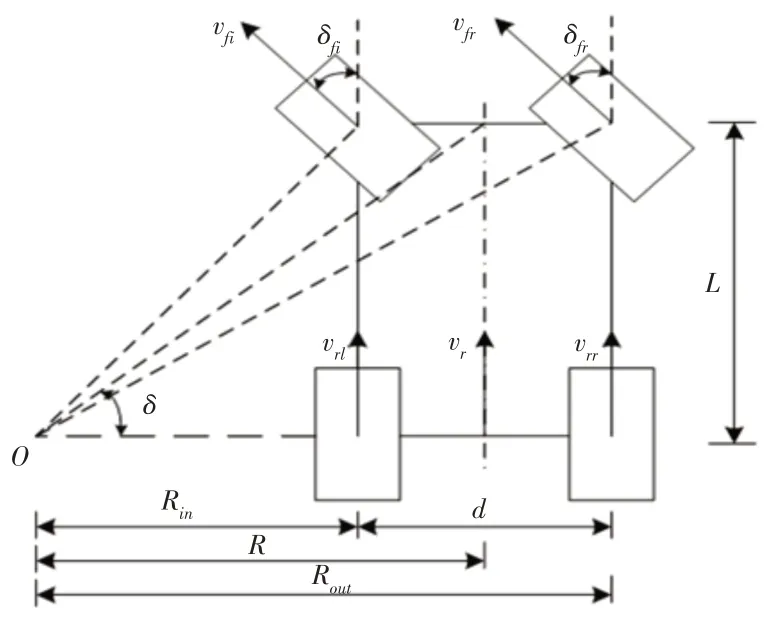
圖1 Ackermann轉向模型Fig.1 Ackermann Steering Model

式中：v—汽車行駛車速；δfl—左側前輪轉向角；δfr—右側前輪轉向角；R—汽車轉彎半徑；Rin—內側驅動輪轉彎半徑；Rout—外側驅動輪轉彎半徑；L—軸距；d—輪距。

2.2 汽車三自由度動力學模型

當汽車行駛速度較快時，其轉向模型更為復雜，為此通常需建立汽車縱向、側向和橫擺三個自由度的動力學模型［11］，如圖2所示。

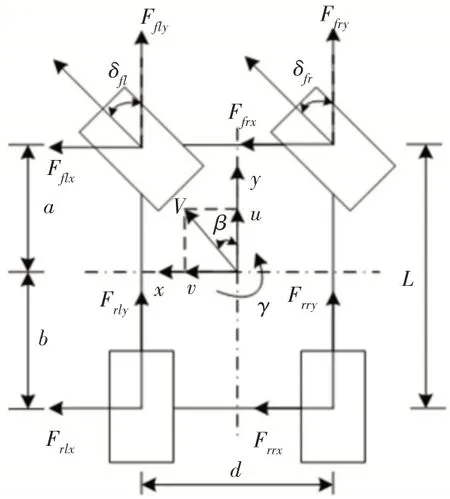
圖2 汽車三自由度動力學模型Fig.2 Three Degree of Freedom Dynamic Model of Automobile

圖中：u—縱向車速；

v—側向車速；

V—質心速度；

β—質心側偏角；

γ—橫擺角速度；

a、b—汽車前、后軸到質心軸線距離；

Fijx、Fijy（ij=fl，fr，rl，rr）—x和y軸方向上的輪胎力。

對汽車三自由度動力學進行分析，可得到電動汽車的輪心速度以及滑移率方程［12］

式中：λij—汽車各車輪的滑移率；

<1)，且各件產品是否為不合格品相互獨立．

ωij—各車輪的轉速；

vij—各車輪輪心速度；

R—車輪半徑。

2.3 系統動力學狀態空間模型

從汽車三自由度動力學模型可以看出，其方程中包含許多非線性因素，難以得到系統的狀態空間表達形式，給控制器設計帶來了困難，為解決這一問題，需對問題進行簡化，將非線性部分線性化，為此假設汽車轉彎過程中保持勻速行駛，且采取后輪驅動前輪轉向模式行駛，也即后輪轉向角近似于0。

定義汽車縱向初始速度為u0，車速的擾動量為Δu，則有：

且可將汽車車輪輪心速度、側偏角以及滑移率簡化為如下方程式［13］。

式中：αij—四個車輪的側偏角；ωij=ω0+Δωij，且ω0=u0/R。

定義X=(Δu，V，γ，Δwfr，Δwrr，Δwfl，Δwrl-Δwrr)T為系統狀態變量，Y=(λfr，λrr，λfl，λrl-λrr)T為系統輸出，則可獲得系統狀態空間表達形式為：

式中：KT—轉矩協調百分比；

H=(1，δ)T，δ—方向盤轉角。

3 電子差速復合控制方法

為解決單種電子差速控制方法存在的固有缺陷，這里提出了高低速復合的電子差速控制方法，當車速小于50km/h 時，基于Ackerman模型提出一種模糊PID控制方法，使汽車車速跟蹤期望車速；當車速大于50km/h時，基于三自由度狀態空間模型，提出一種基于模糊逼近的滑移率優化控制方法，使實際相對滑移率跟蹤期望相對滑移率，控制系統結構，如圖3所示。

圖3 控制系統框圖Fig.3 Block Diagram of Control System

3.1 模糊PID速度控制器

車輛轉彎時，當判斷車速小于50km/h，基于汽車Ackermann轉向模型，以車速為輸入，根據式（1）～式（4），可求解出四個車輪的期望速度，通過設計模糊PID控制器，使得車輪實際速度跟蹤期望輪速，控制流程圖，如圖4所示。控制器設計過程如下。

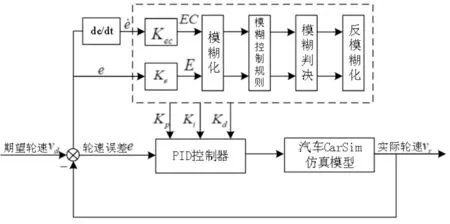
圖4 低速模糊PID控制原理圖Fig.4 Schematic Diagram of Low Speed Fuzzy PID Control

（1）模糊控制器輸入及輸出變量的模糊化。將期望車速與實際車速誤差及誤差變化率的量化論域E、EC取為｛-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6｝，模糊子集為｛負大（NB），負中（NM），負小（NS），零（ZE），正小（PS），正中（PM），正大（PB）｝；將輸出變量的量化論域P取為｛2，3，4，5，6，7，8，9，10｝，量化論域I、D則均取為｛0，0.6，1.2，1.8，2.4，3，3.6，4.2，4.8｝，模糊子集為｛零（ZO），小（S），中（M），大（B），最大（L）｝。

（2）模糊規則的建立。建立如下模糊規則：當期望車速與目標車速誤差 |e|較大時，Kp取較大值、Ki、Kd取較小值；當誤差 |e|和變化率|為中等大小時，Kp取較小值、Ki、Kd取適中值；當誤差 |e|較小時，Kp、Ki取較大值、Kd取較小值；

（3）模糊推理和解模糊。這里直接采用Matlab 中提供的Takagi-Sugeno-kang模糊邏輯推理算法。

3.2 基于模糊逼近的滑移率優化控制器

車輛轉彎時，當判斷車速大于50km/h，基于汽車三自由度狀態空間模型，令驅動輪相對滑移率的期望值為Δλ*，并定義滑移率誤差函數為：

則獲得基于滑移率的誤差狀態方程形式為：

也即：

文獻［12］對上述狀態空間表達式中的矩陣A和矩陣B進行了具體的推導，但其獲得的結果較為復雜，計算量大，且在推導過程中忽略，導致存在建模誤差，為此這里提出利用模糊系統萬能逼近特性對這兩個矩陣進行在線逼近，避免了復雜建模過程，在此基礎上提出基于LQR的優化控制器，具體過程如下。

（1）慣性參數矩陣在線逼近，對系統進行模糊建模。

定義模糊系統輸出函數形式如下［13］：

式中：ξ(x)=(ξl(x)，…，ξM(x))—回歸向量；

Θ=(θl，…，θM)T—參數向量；

Y(x)—模糊系統輸出向量；

l—式隸屬度函數個數；

M—模糊規則總條數；

ξl(x)—模糊基函數，形式如下：

考慮系統慣性參數矩陣A、B計算量較大且存在建模誤差，利用模糊系統的萬能逼近特性，建立系統的自適應模糊模型。

設計l=3條模糊系統高斯隸屬度函數為：

選取模糊規則總條數M=32，得到其逼近矩陣分別為：

則系統的模糊狀態空間表達形式為：

式中：θ、β—自適應調節參數向量。

（2）LQR控制器設計。

則，根據滑移率的誤差狀態方程的模糊表達形式，可設計優化控制律為：

式中：矩陣Q—半正定的常數矩陣；

R—正定常數矩陣；

P—正定矩陣，且滿足狀態黎卡提方程：

（3）滑模補償控制器設計。

為克服狀態空間方程中干擾項h(x，t)以及模糊逼近帶來的誤差，可根據滑模控制理論，在控制器式（20）基礎上，引入滑模魯棒控制項。

定義系統滑模面為：

綜上，基于模糊逼近的滑移率優化控制律為：

4 仿真實驗

為驗證所提方法有效性，通過Simulink/Carsim 聯合仿真平臺，選擇雙移線道路工況，分別設置車速v=80km/s、v=30km/s進行高低速仿真，并設置車輛參數，如表1所示。

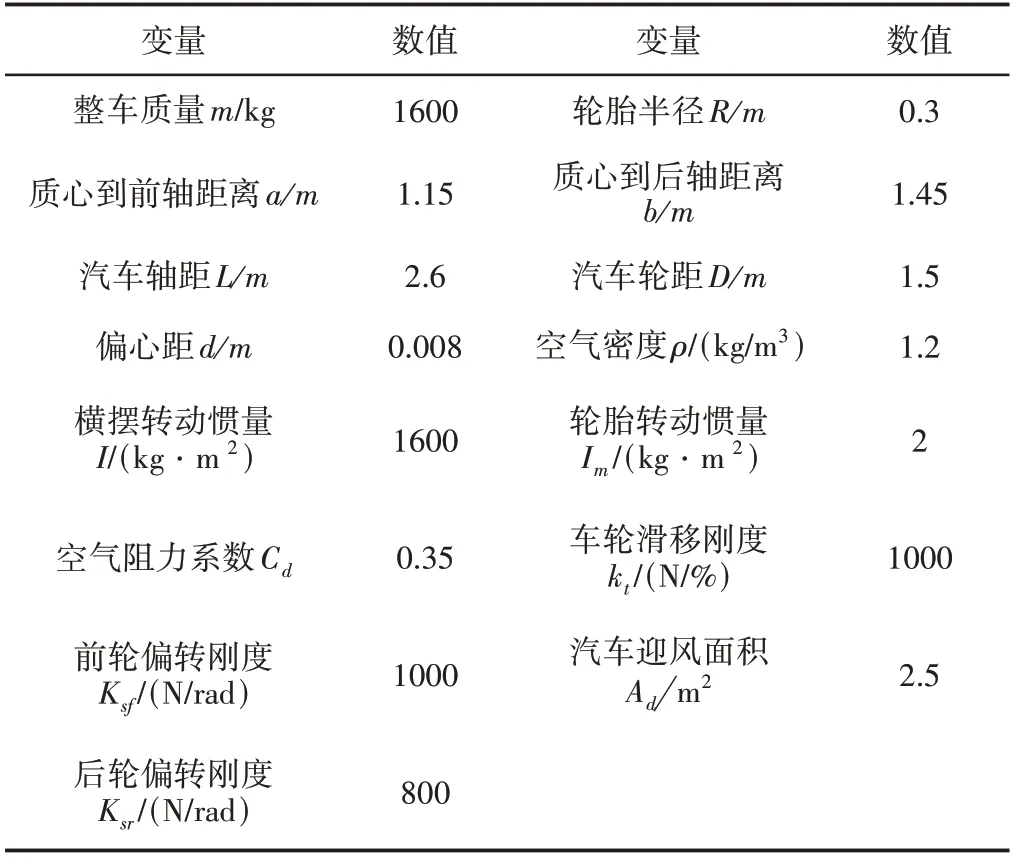
表1 汽車模型參數Tab.1 Car Model Parameters

4.1 低速行駛仿真驗證

以后輪驅動的輪轂式電動汽車為對象，選擇雙移線道路工況，期望車速設置為v=30km/s，分別采用傳統PID控制方法以及這里提出的模糊PID控制方法進行仿真結果，如圖5～圖7所示。

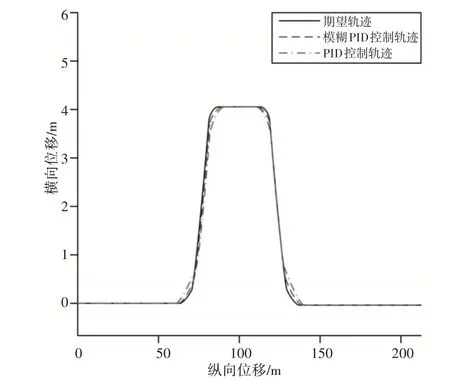
圖5 汽車行駛軌跡Fig.5 Vehicle Trajectory

從圖5可以看出，當汽車以較低速度行駛在較簡單道路工況且無外部擾動情況下，通過對輪速的跟蹤，傳統PID控制方法以及這里方法均能實現汽車的穩定行駛且跟蹤期望路徑，對比兩種控制方法，可以看出在彎道部分這里控制方法的跟蹤精度較傳統PID控制方法有一定程度提高。

汽車車速的跟蹤情況，如圖6 所示。驅動輪輪速的跟蹤情況，如圖7所示。從仿真結果可以看出，兩種差速控制方法均能實現汽車驅動輪輪速的穩定跟蹤，從而實現汽車車速對目標車速的穩定跟蹤，對比兩種控制方法，可以看出這里控制方法在跟蹤精度上較傳統PID控制方法有一定程度提高。

圖6 汽車行駛速度跟蹤Fig.6 Vehicle Speed Tracking

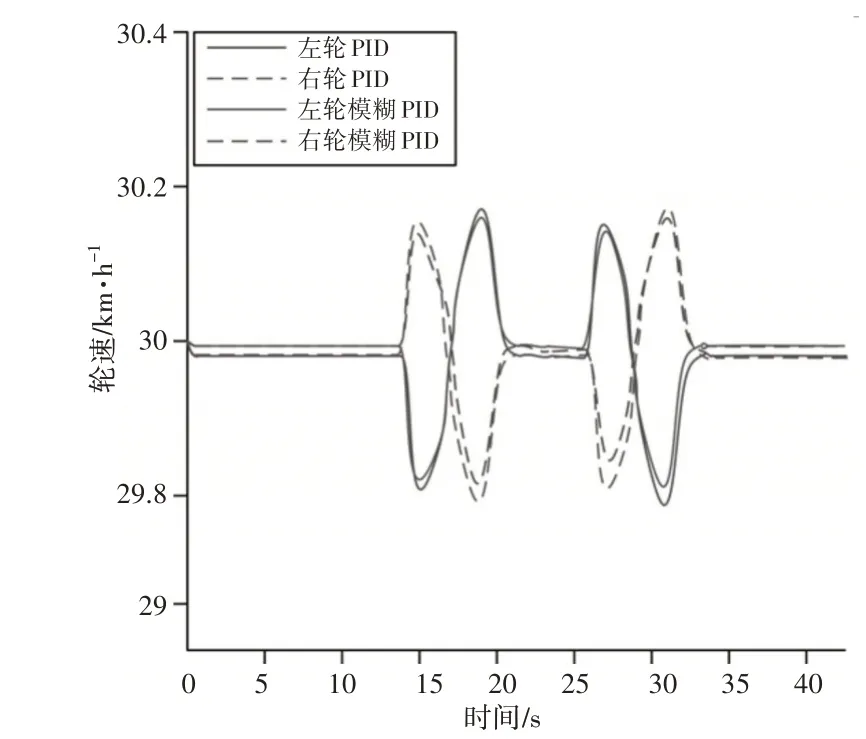
圖7 驅動輪速度變化Fig.7 Drive Wheel Speed Change

4.2 高速行駛仿真驗證

選擇弧形的道路工況，汽車勻速右轉，期望的車速設置為v=80km/s，轉彎弧度設置為δ=2°，采用這里提出的滑移率控制方法進行仿真結果，如圖8、圖9所示。在汽車無滑移率控制器和采用這里提出的滑移控制方法情況下的一組對比仿真結果，如圖8、圖9所示。從中可以看出，當不施加滑移率控制器進行彎道行駛時，左驅動輪的滑移率明顯大于右驅動輪，兩輪存在一定的相對滑移率，這會導致車胎磨損且發生滑轉，導致汽車行駛不穩定；當采用這里滑移率控制方法時，左右驅動輪的滑移率保持一致，即相對滑移率迅速收斂為0，使汽車行駛進入穩定狀態。

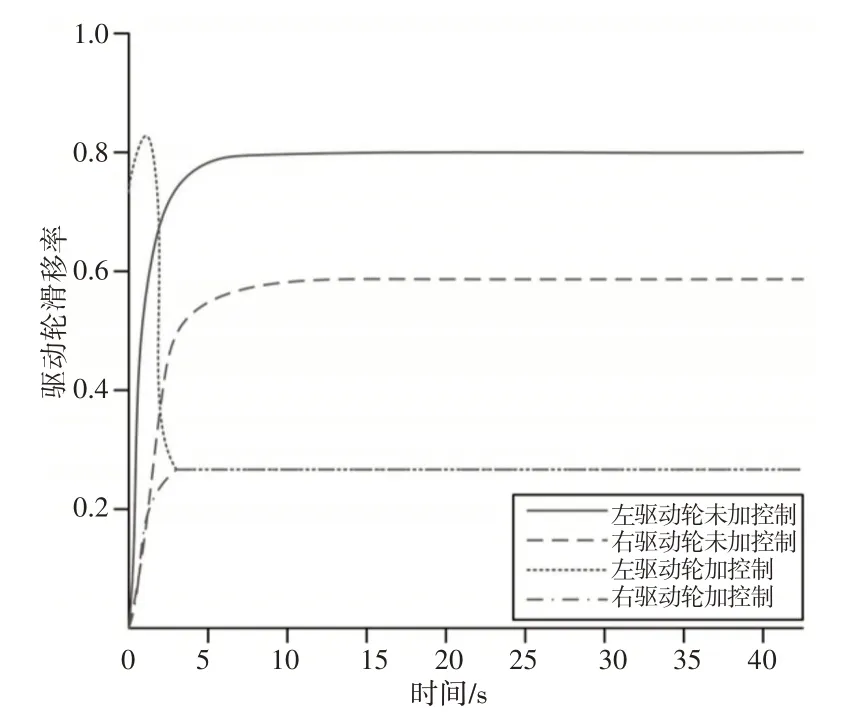
圖8 汽車行駛驅動輪滑移率Fig.8 Wheel Slip Rate of Driving Vehicle

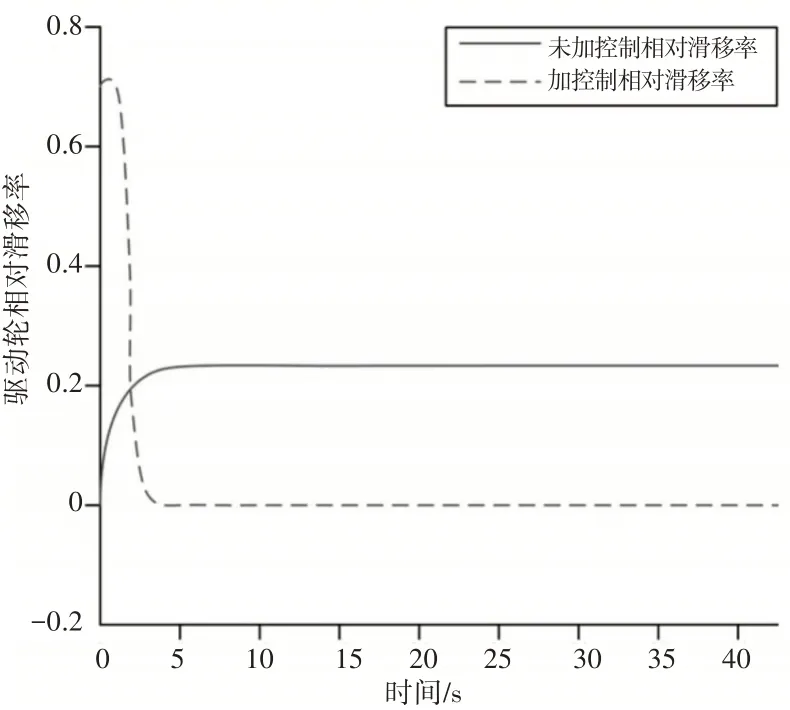
圖9 汽車行駛驅動輪相對滑移率Fig.9 Relative Slip Ratio of Driving Wheel

為進一步驗證這里所提控制方法的優越性，在設置汽車參數時，給出一定的偏差值，使得系統存在建模誤差時，而后分別采用LQR 滑移率控制方法與這里控制方法進行對比仿真結果，如圖10、圖11所示。

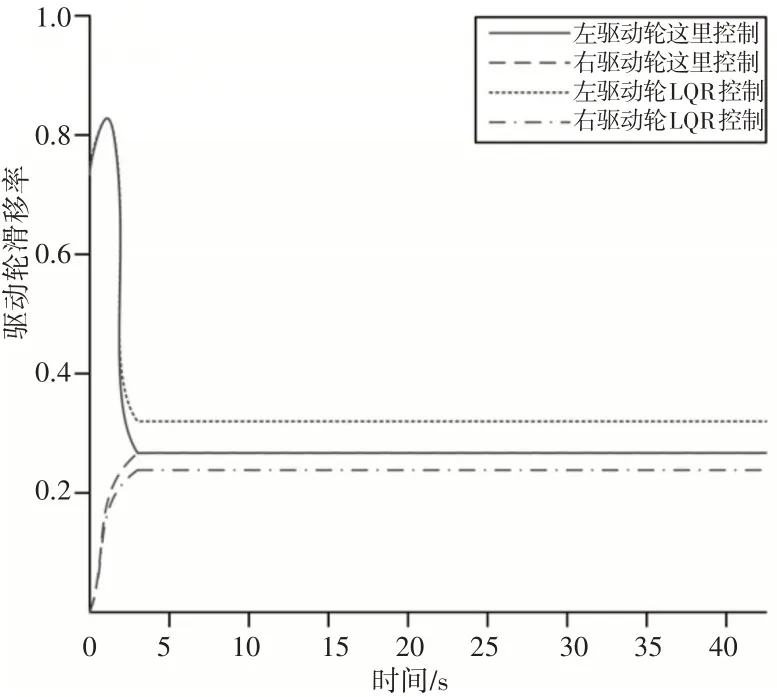
圖10 汽車行駛驅動輪滑移率Fig.10 Wheel Slip Rate of Driving Vehicle

圖11 汽車行駛驅動輪相對滑移率Fig.11 Relative Slip Ratio of Driving Wheel

從圖10、圖11的仿真結果可以看出，當采用傳統LQR控制方法時，其相對滑移率有收斂的趨勢，且在仿真時間t=3s達到穩定狀態，但由于系統存在建模誤差，其左驅動輪的滑移率為0.32，而右驅動輪的滑移率為0.21，始終存在0.11的誤差，其相對滑移率無法收斂至零。而在這里方法的控制下，雖然存在系統建模誤差，汽車左右驅動輪的滑移率均t=3s時達到0.28，其相對滑移率收斂至0，從而實現汽車的穩定控制。綜上仿真結果，無論汽車是處于高速行駛還是低速行駛狀態，在這里所提的高-低速復合控制方法作用下，均能實現對汽車的穩定控制。

5 結論

這里重點針對不同速度狀態下輪轂式電動汽車轉向的電子差速穩定控制問題，提出了一種高-低速復合控制方法，較好的解決了PID、滑模、自適應等傳統電子差速控制方法對汽車行駛速度要求較高的局限性。當汽車處于低速行駛狀態時，建立了汽車Ackermann轉向模型，并基于傳統PID控制方法，構建模糊規則在線調整PID參數，提出一種模糊PID電子差速控制方法，降低了系統超調量、提升系統響應速度，從而減小了速度跟蹤誤差；當汽車處于高速行駛狀態時，構建了汽車三自由度模型，進一步利用模糊系統的逼近特性，建立系統模糊模型，并基于LQR原理提出了電子差速的滑移率優化控制方法，在有效克服建模誤差帶來的影響的同時，實現了相對滑移率快速收斂，提高了汽車行駛的穩定性。