帶有延遲步長的循環(huán)BB梯度法

楊奕涵

(重慶師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 重慶 401331)

考慮一般無約束優(yōu)化問題

(1)

其中目標(biāo)函數(shù)f:Rn→R是連續(xù)可微的。求解問題(1)的方法主要有線搜索方法和信賴域方法, 而梯度法是線搜索方法中的一類簡單迭代方法, 它以負(fù)梯度方向作為搜索方向, 其迭代格式為

xk+1=xk-αkgk,

(2)

其中g(shù)k?g(xk)=?f(xk),αk為步長。由于搜索方向已定, 梯度法求解無約束優(yōu)化問題便轉(zhuǎn)化為研究步長αk的選取, 不同的步長選取會(huì)導(dǎo)致梯度法具有不同的性能。因此, 如何設(shè)計(jì)一個(gè)有效的步長, 使得問題(1)能被快速求解, 且收斂性具有一定的理論保證, 是研究梯度法的重要問題之一。

最早的梯度法是1847年Cauchy[1]采用精確線搜索步長, 提出了最速下降法(SD法), 其步長為

(3)

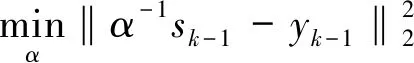
其中sk-1=xk-xk-1,yk-1=gk-gk-1, 得到兩個(gè)兩點(diǎn)步長公式為

兩點(diǎn)步長又稱為BB步長, 相應(yīng)的梯度法稱為BB梯度法, 簡稱BB法。對于f為嚴(yán)格凸二次函數(shù)的情形, Barzilai和Borwein證明了當(dāng)n=2時(shí), BB法具有R-超線性收斂速度。自BB法的提出, 極大地改善了梯度法的效率, 其理論上的結(jié)果有: 1993年Raydan[3]證明了當(dāng)f為任意維嚴(yán)格凸二次函數(shù)時(shí), BB法是全局收斂的, 并且2002年Dai和Liao[4]進(jìn)一步證明了BB法具有R-線性收斂速度。此外, 也吸引了眾多學(xué)者對該方法做一系列研究, 從不同的角度推導(dǎo)了不同類型的BB步長, 如文獻(xiàn)[6]-[15]等。

如果直接將BB法推廣至求解一般無約束優(yōu)化問題, 即使目標(biāo)函數(shù)是嚴(yán)格凸函數(shù), 該方法也可能不收斂。因此為保證其收斂性, Raydan[5]在1997年首次將BB步長與GLL非單調(diào)線搜索技術(shù)[16]相結(jié)合, 并證明了該方法是全局收斂的。隨后, 求解一般無約束優(yōu)化問題的BB類方法得到發(fā)展, 如文獻(xiàn)[17]-[19]等。……