面向虛擬編組的城市軌道交通運行優化調度方法

付 兵，馬新源，田婉琪，賴成紅

(1.成都工業職業技術學院 軌道交通學院，四川 成都 610218；2.北京交通大學 電子信息工程學院，北京 100044；3.北京交通大學 軌道交通運行控制系統國家工程研究中心，北京 100044)

0 引言

城市軌道交通具有運能大、速度快的特點，作為解決城市交通問題的最佳方案之一，在疏解城市交通壓力方面發揮了顯著的作用[1-2]。隨著信息技術的發展，目前基于無線通信的列車控制系統(CBTC)得到了廣泛應用。該系統通過無線通信實現了車地雙向通信，大幅度提高列車區間通過能力[3]。然而CBTC 系統的性能已趨于飽和，而且現有CBTC系統受限于地面設備的布置，且列車運行方式不夠靈活，無法有效應對潮汐客流，在一些特殊時間段內，城市軌道交通的運行仍存在潛在的安全隱患[4]。例如，當車站客流過大時，站臺空間內異常擁擠的人流對列車的正常運營帶來嚴重的安全風險[5]。現有的解決方案主要是限制進入站臺的乘客數量、減緩乘客進站速度以及采取臨時疏導措施，無法從根本上解決大客流量時段下乘客高度聚集的問題。

目前，基于虛擬編組的列車運行控制方式受到了越來越多的關注。與傳統編組方法相比，虛擬編組的列車之間不再使用機械掛鉤相連接，而是采用車-車無線通信技術的虛擬連掛方式，將多輛列車虛擬連掛運行。虛擬編組控制方式下，列車的運行調度方式將發生相應的改變，即根據乘客需求[6]，求出站點停留時間、連續站點間運行時間以及列車間距和編組狀態的最優解。適當的列車調度指揮能提高列車運行效率[7]，并在客流高峰期盡可能地減少乘客的候車時間。列車調度問題作為軌道交通列車運行控制系統中的一個重要問題，既有文獻已進行了深入研究。Wong等[8]針對非周期時刻表的調度同步問題提出了一個混合整數規劃優化模型，該模型最小化所有乘客的換乘等待時間，并根據客流的變化對列車的停留時間進行了相應的調整；該模型更加靈活且更加符合乘客的需求，同時也提高了城市軌道交通通行效率。Sun 等[9]提出了一種基于乘客需求的列車停留時間模型的地鐵線路列車調度優化方法，在車頭時距方程、乘客人數方程和列車停留時間方程的約束下，建立列車調度優化模型；在綜合考慮乘客候車時間和列車利用率的情況下，得出最優調度方案。Yin 等[10]提出了線性規劃模型，并將列車調度優化模型[9]中的非線性問題轉化為線性問題。Zhang等[11］通過卡爾曼濾波方法校正采集的列車數據，利用運動學定理和最小二乘法進行濾波，獲得高質量的列車運行數據，并引入列車誤點數、列車跳停方式等概念[12-14]來優化列車調度方案。

既有研究已經提出虛擬編組技術框架[15-17]，然而對于虛擬編組下運行調度的技術細節還缺乏深入探討。基于此，提出一種時刻表和編組策略的協同優化方法，以實現列車利用率和乘客等待時間之間的平衡，對列車運行調度進行優化，從而提高城市軌道交通運行效率，節約運行成本。以北京地鐵亦莊線為研究對象，對所提出的列車運行調度方法進行分析，驗證所提出優化調度方法的有效性。

1 列車運行與調度模型的建立

首先，建立列車運行過程的模型，用于描述車頭時距和乘客人數的動態變化。然后采用二進制變量描述列車虛擬編組。基于現有條件，提出如下假設：①假設虛擬編組所使用的列車數最多為3 列；②假設虛擬編組所使用的列車是默認情況下來自車站的列車；③假設該計劃完成后列車將自動返回車站。

1.1 列車運行模型

列車運行圖如圖1 所示，其描述了列車運行過程中相關參數的變化，On，s表示列車n在車站s- 1和車站s之間的運行時間，s；dn，s表示當列車到達車站s時，列車n和列車n- 1 的車間距，s；tn，s表示列車n在s站的停留時間，s。假設列車在相鄰2 個車站之間的運行時間不變，則列車間距的動態變化可以表示為

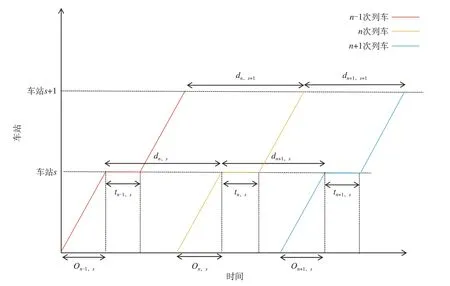
圖1 列車運行圖Fig.1 Train working diagram

列車運行過程中，車上的乘客人數的動態變化可以表示為

式中：pn，s表示n次列車離開s站時列車上的乘客人數，人；pin，s表示從s站進入n次列車的乘客人數，人；pnn，s表示n次列車留在s站的乘客人數，人。

根據參考文獻[18]，pnn，s與n次列車到達s站時的乘客人數成正比，可以表示為

式中：rn，s表示n次列車上從s站出發的乘客人數的比例，其值可根據歷史乘客數據進行估計。

當n次列車離開s站時，進入站臺的列車數量與在該站等待的人數呈負相關，該站等待人數的動態方程表示為

式中：pwn，s表示在s站等待的乘客人數，人；an，s表示n- 1 次列車到達后、n次列車到達s站前的乘客到達率；dn，san，s表示n次列車到達s站前進入站臺的乘客人數，人。

特別是處于客流高峰時段，列車無法運載所有在站臺等待的乘客，故在站臺等待的人數pwn，s通常大于0。

從s站進入n次列車的乘客數量與列車到達s站前在站臺上等待的乘客人數和列車的剩余容量相關。其中站臺上的等候人數為原有等候人數與后進入站臺的乘客人數之和，即pwn-1，s+dn，san，s，而n次列車的剩余容量是列車的最大容量Cmax與處于虛擬編組中的所有列車的乘客容納量(1 -rn，s)pn，s-1的差。δn，n'是列車的虛擬編組指數。在s站進入n次列車的乘客人數表示為

具體來說，從s站進入n次列車的乘客人數是列車到達s站之前在站臺上等待的乘客人數和列車的剩余容量中的最小值。

根據公式⑴至公式⑸，列車上的乘客人數和站臺上的等待人數可分別表示為

特殊情況下pn，0= 0且pw0，s= 0。

公式⑴、公式⑵分別給出了列車車頭時距和乘客人數的動態變化方程，公式⑶、公式⑷、公式⑸描述了列車上下車人數的變化。其中pwn，s，pn，s，rn，s和an，s是系統的狀態變量，d1，s和tn，s是決策變量，并且d1，s和tn，s由協同優化模型的優化結果決定。

1.2 基于虛擬編組的列車控制

基于虛擬編組的列車運行示意圖如圖2 所示。圖2 中的線路上共有2S個車站，起點站為1 號站，終點站為S號站。該線路上的列車根據實際需求，可自行解編或重聯。假設列車在車站內進行虛擬重聯，前車到站后等待后車進站，在站內進行重聯后以虛擬編組狀態發車。若線路客流較小，虛擬編組列車可通過前車加速、后車減速的形式在站間解編，切換為快慢車運行方式。到達終點站后，列車可以通過道岔轉入上行線路運行，最終返回2S號站。當到達2S號站時，列車將面臨虛擬編組或者返回站臺。對于已編組的列車，需要決定是否解編或以當前編組狀態繼續執行下一個服務。如果目前處于客流高峰時段，單組列車將會在站臺進行重聯，即與下一列車形成虛擬編組。虛擬編組列車繼續從1號站出發，直到返回2S號站。

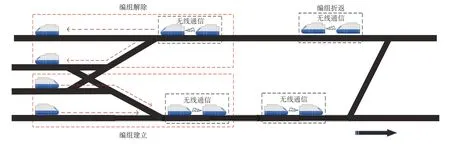
圖2 基于虛擬編組的列車運行示意圖Fig.2 Train working diagram based on virtual coupling

如果n次列車在另一列n'次列車之后執行服務，那么n次列車和n'次列車之間的編組狀態可以用δn，n'(n'＞n)來表示

n'次列車的到達時間和n次列車的發車時間符合以下限制條件。

假設列車總數量固定為M，且線路上的初始列車數量為Ntrain，則虛擬編組所使用的列車數量必須滿足可用列車數量，其定義為

式中：二進制變量φn，n'表示當n'次列車進入線路且n次列車處于虛擬編組狀態時，n'次列車的出發時間是否合理。

φn，n'的定義為

式中：tin表示n次列車進站所需要的時間，s。

公式⑿方程左側表示n次列車在線路上運行1 個周期所花費的時間，右側表示n次列車的合理發車時間。如果方程滿足條件，則列車的發車時間是合理的，即φn，n'= 1，否則φn，n'= 0。

2 模型優化及求解方法

2.1 優化模型

模型的優化目標側重于列車利用率和乘客出行體驗2 個方面。首先，為了提高列車運行過程中的車廂的滿載率，需要對列車編組指標進行最大化可表示為

式中：K1為列車的編組指標。

其次，客流量會因高峰時段的乘客人數變化而發生很大波動。因此，優化目標需保證在不同乘客到達率下，減少乘客的旅行時間，包括乘車時間和候車時間，可表示為

式中：K2為乘客的乘車時間；K3為乘客的候車時間。

綜上所述，列車時刻表的優化模型可以表示為

式中：γ1，γ2和γ3為權重系數，且γ1+γ2+γ3= 1。

約束條件可表示為

2.2 模型轉換和求解

協同優化模型包含整數變量、連續變量和二元變量。該模型的目標函數是線性的，約束條件中包含非線性約束，需要將約束條件中的非線性公式轉化為線性約束再利用商業求解器進行求解。要將進入列車的乘客人數pin，s、列車上原有的乘客人數pwn，s和站臺上等待的乘客人數pn，s等非線性約束條件轉化為線性約束條件，需要遵循以下3 個性質。

（1）連續變量f(x) ≤0 等價于邏輯變量k= 1，需要遵循以下約束條件。

（2）設輔助變量y=kf(x)，遵循以下約束條件。

（3）設輔助邏輯變量k3=k1k2，遵循以下約束條件。

基于以上線性化方法對原優化模型進行轉化后的協同優化模型為

約束條件為

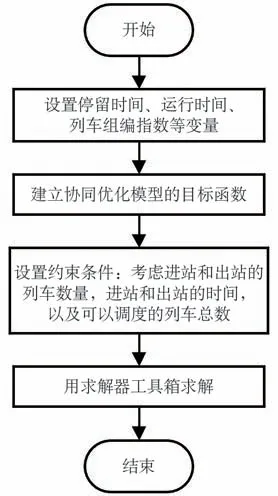
圖3 模型求解流程Fig.3 Flow of model solution

3 數值仿真

以北京地鐵亦莊線為研究對象，通過數值實驗證明上述優化模型的有效性。北京地鐵亦莊線是一條有14 個車站的通勤線路，從宋家莊到次渠為上行方向，從次渠到宋家莊為下行方向。研究時間為6：00—8：30 的高峰時間，共有16 列在運列車。以列車編組指標最大化、列車停站時間及乘客候車時間最小化為優化目標，建立優化模型公式⒃和線性約束條件公式■2，利用規劃求解器工具箱求解，進而完成對北京地鐵亦莊線虛擬編組運行的優化。模型參數表如表1所示。

表1 模型參數表Tab.1 System parameters

列車停站時間表如圖4 所示，為進行虛擬編組后，16列列車在各站臺停留的時間。從圖4中可以看出，列車運行到4號、13號站臺時停留時間開始增加，在5號、13號和14號站臺的停留時間達到頂峰，是因為以上站點緊鄰人口密集的居民區，虛擬編組后在早高峰時段承運了更多的乘客流量。雖然早高峰時段各列車的停留時間仍然較長，但與固定的停留時間相比，一定程度上提高了城市軌道交通列車的運行效率，減少了乘客的等待時間。

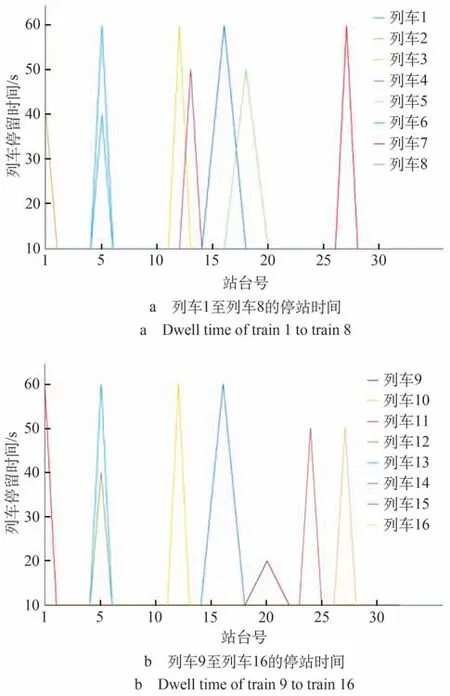
圖4 列車停站時間表Fig.4 Train dwell time

列車行車時刻表如圖5 所示。結合圖4 和圖5進行分析，可以發現列車在4 號站臺停留的時間開始增加，其對應時刻為7：00 左右，此時列車在上行線路上停留了更長時間，客流也更密集。如果不進行虛擬編組，就會因站臺上等待的乘客和列車上承載的乘客數量過多而產生潛在的安全隱患。經過虛擬編組優化后，列車1與列車13進行虛擬編組來執行列車13 服務，列車2 和列車14 進行虛擬編組來執行列車14 服務，以此來增加列車的承載能力，在減少高峰期乘客的候車時間的同時，也減少了站臺滯留乘客的數量。

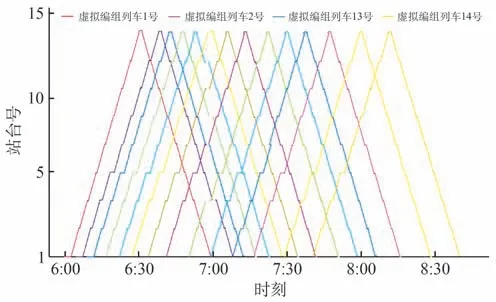
圖5 列車行車時刻表Fig.5 Train schedule

列車到達前，站臺上乘客候車時間表如圖6 所示，通過求解優化模型公式⒃中乘客候車時間K3得到。在列車運行和往返過程中，乘客的候車時間不斷變化，但均相對較短。可以看出，相對調整前，虛擬編組已極大地節省了乘客的候車時間。

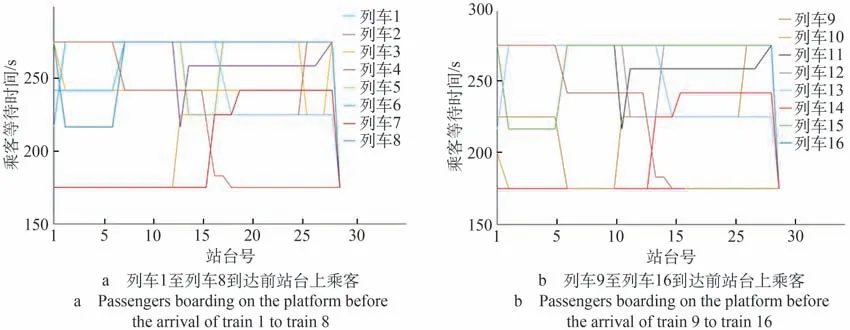
圖6 乘客候車時間表Fig.6 Passengers waiting time

虛擬編組后的列車間距如圖7所示。從圖7中可以看出經過虛擬編組優化后，16列在運列車彼此間的追蹤間隔會根據客流的動態變化而調整，從而有效地緩解高峰時期客流壓力，并在客流低峰期節約運力。在傳統的列車調度方案中，列車發車間隔時間及列車間距是根據歷史客運量確定的一個固定值。虛擬編組前的列車間距固定為390 s，虛擬編組后的相鄰列車間距最小為180 s，平均間距為347 s，其列車運行效率提高了11.03%。

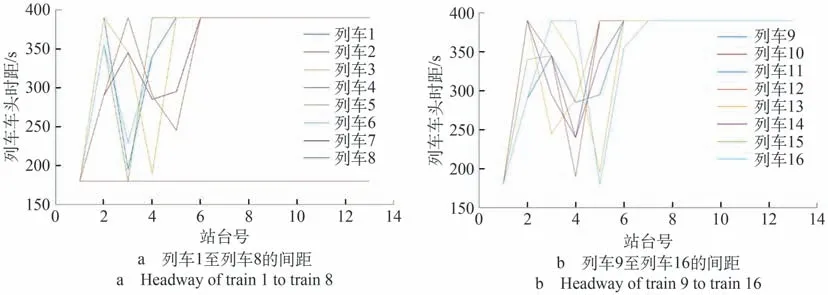
圖7 列車間距Fig.7 Train headway

由以上分析可以發現，與傳統的列車調度方案相比，虛擬編組后的列車可以有效地應對潮汐客流。通過虛擬編組可以有效地提高列車的運行效率、減少乘客的候車時間，且通過制備非平衡的列車調度表可以實現運營方和乘客利益的協同優化。

4 結束語

面向虛擬編組的城市軌道交通運行優化調度方法，在充分考慮車頭時距和乘客人數動態變化情況下，構建列車運行控制模型，采用協同優化模型獲取列車停留時間、乘客候車時間、列車利用率3 類指標，能有效反映高峰時段客流時空分布特征，提出的基于虛擬編組的列車優化調度方法可以合理地解決列車運行和停留時間的安排問題。數值仿真實驗中，協同優化模型與不均衡列車優化調度方法適用于北京亦莊線通勤線路，模擬運行結果表明，該模型能合理地安排停留時間、協調運力，進而提高列車利用率，減少乘客候車時間。