鐵路樞紐雙編組站靜態(tài)配流協(xié)同優(yōu)化研究

戶佐安，朱 雨，怡智航，陳 將

(1.西南交通大學 交通運輸與物流學院，四川 成都 611756；2.西南交通大學 綜合交通大數(shù)據(jù)應用技術國家工程實驗室，四川 成都 611756；3.西南交通大學 綜合交通運輸智能化國家地方聯(lián)合工程實驗室，四川 成都 611756；4.中國鐵路成都局集團有限公司 遂寧車務段，四川 遂寧 629000)

0 引言

編組站是鐵路運輸重要的基層生產(chǎn)單位，優(yōu)化編組站配流方案對加速車輛周轉、提高運輸能力具有重要意義。我國部分鐵路樞紐擁有2 個及以上編組站，并且存在樞紐內(nèi)資源利用不合理的情況，為優(yōu)化樞紐內(nèi)運輸組織的整體水平，達到全局最優(yōu)，整體考慮樞紐內(nèi)2 個編組站的車流，進行鐵路樞紐雙編組站靜態(tài)配流協(xié)同優(yōu)化研究，這對于促進樞紐內(nèi)車輛周轉，提升鐵路樞紐運輸能力具有較強的現(xiàn)實意義。目前國內(nèi)外學者針對編組站配流相關問題已展開不少研究。Haahr 等[1]構建混合整數(shù)規(guī)劃模型，對分類線運用子問題設計貪婪啟發(fā)式算法進行求解；Gestrelius等[2]綜合考慮到發(fā)線運用及解體方案，構建整數(shù)規(guī)劃模型進行求解。Jing 等[3]將編組站的技術作業(yè)過程描述為流水作業(yè)過程，建立靜態(tài)配流網(wǎng)絡模型并采用禁忌搜索算法求解。馬亮等分別構建了靜態(tài)配流字典序多目標積累調(diào)度模型[4]和動態(tài)配流分層模型[5]。趙金觀等[6]以正點出發(fā)列車數(shù)最多為目標，建立廣義動態(tài)配流問題模型；唐金金等[7]以全服務網(wǎng)絡總旅行費用最小為目標，建立服務網(wǎng)絡動態(tài)配流優(yōu)化模型；郭瑞等[8]研究多階段優(yōu)化方法的調(diào)度策略及啟發(fā)式規(guī)則，設計多階段分層啟發(fā)式配流算法求解；薛鋒等[9]將編組站資源可用度引入編組站配流模型，利用分層優(yōu)化方法求解；李晟東等[10]著眼于提高運輸時效性，將貨物運到期限引入配流優(yōu)化模型，并采用模擬退火算法求解；許可等[11]建立基于車流接續(xù)代價最小的編組站配流優(yōu)化模型并設計相應算法求解。于婕等[12]以優(yōu)先級加權的貨物總在站停留時間最小和發(fā)出總車輛數(shù)最多為雙目標建立動態(tài)配流優(yōu)化模型。上述文獻均基于單編組站為研究主體進行配流優(yōu)化，未考慮跨編組站車流的協(xié)同性，僅有陳磊[13]提出構建基于編組站綜合自動化系統(tǒng)(CIPS)的跨站協(xié)同運輸計劃編制平臺；武旭等[14]以兩技術站正點出發(fā)列車數(shù)最多為目標，構建技術站間貨物列車協(xié)同配流模型。

綜上所述，部分文獻考慮了車輛在站停留時間作為優(yōu)化目標，但忽略了出發(fā)列車的等級高低及車流分配優(yōu)先性。且大部分文獻在進行配流的協(xié)同優(yōu)化時以車站內(nèi)部作業(yè)之間的協(xié)同為主，忽略了編組站間車流分配的協(xié)同。在已有研究的基礎上，從樞紐內(nèi)編組站間協(xié)同配流的角度出發(fā)，研究鐵路樞紐雙編組站靜態(tài)配流協(xié)同優(yōu)化問題，為編組站配流問題的優(yōu)化提供一定的參考。

1 問題描述

雙編組站靜態(tài)配流協(xié)同優(yōu)化問題可描述為：中轉車流隨部分改編中轉列車或到達解體列車陸續(xù)到達樞紐內(nèi)兩編組站，當制定某一編組站的配流方案時，全局考慮兩編組站的到達車流。樞紐內(nèi)車站分布示意圖如圖1所示，若P站某一去向(如f去向)到達車流不足致使列車無法正點滿軸開行時，將Q站f 去向的符合接續(xù)時間要求的車流編入小運轉列車送至P站，參與編組，保證列車滿軸且正點開行。

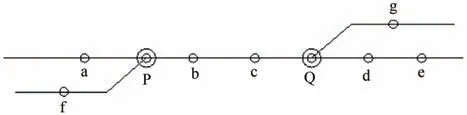
圖1 樞紐內(nèi)車站分布示意圖Fig.1 Station distribution within the hub

2 模型構建

2.1 模型假設

（1）樞紐內(nèi)2個編組站分工方案既定。

（2）樞紐內(nèi)兩編組站采用單推單溜作業(yè)方式，兩編組站分別由一臺調(diào)車機車負責解體作業(yè)、一臺調(diào)車機車負責編組作業(yè)。

（3）列車按照到達計劃到達車站，不考慮波動性。

（4）車站接發(fā)車能力及容車能力充足，線路區(qū)間通過能力充足。

（5）列車解編順序采取先到先解、先發(fā)先編原則。

2.2 目標函數(shù)

目標函數(shù)1 為雙編組站配流總代價最小，目標函數(shù)2為雙編組站的總滿軸列車數(shù)最多。

式中：Z1表示雙編組站配流總代價；Z2表示雙編組站 總 滿 軸 列 車 數(shù)；i(i= 0，1，2，...，m) 與i'(i'=0，1，2，...，m')分別為P 站和Q 站到達列車索引，i= 0 與i'= 0 分別表示本階段開始時P 站與Q 站的站存車，m與m'分別表示P 站與Q 站的到達列車索 引 最 大 值；j(j= 1，2，...，n，n+ 1) 與j'(j'=1，2，...，n'，n'+ 1)分別為P 站和Q 站出發(fā)列車索引，j=n+ 1 與j'=n'+ 1 分別表示本階段結束時P 站與Q 站未被編組的站存車；k(k= 1，2，...，p)為去向索引，p表示去向索引最大值；ci，k，j為到達列車i中k去向車組為出發(fā)列車j供應車流的代價，ci'，k，j，ci，k，j'和ci'，k，j'同理；xi，k，j表示到達列車i中去向為k的車組為本站出發(fā)列車j提供的車流量，xi'，k，j，xi，k，j'和xi'，k，j'同理；yj表示出發(fā)列車j是否滿軸，yj'同理，若滿軸，其值為1，否則為0。

其中，配流代價的確定方法參考文獻[15]，若列車違編或到達列車與出發(fā)列車的接續(xù)時間超過了最小接續(xù)時間限制，其配流代價視為一充分大正數(shù)。其余出發(fā)列車按其等級以直達、直通、區(qū)段、摘掛、小運轉的順序排列，對等級相同的列車，按其編組去向數(shù)升序排列，對等級和編組去向數(shù)均相同的列車按其出發(fā)時刻由早到晚排列。以序號作為配流代價，具體計算公式見公式—。

2.3 約束條件

（1）車流量約束。

式 中：li，k表 示 到 達 列 車i中k去 向 的 車 數(shù)，li'，k同理。

公式⑶和⑷表示樞紐內(nèi)兩編組站的到達列車中k去向的車輛數(shù)之和等于出發(fā)列車和階段結束時站存車中k去向的車輛數(shù)之和。

（2）車流接續(xù)時間約束。

式中：T為到達列車i的解體作業(yè)最早開始時刻，同理；表示到達列車i的到達時刻，其中T為本階段開始時刻，T同理；TDJ為到達列車的技術作業(yè)時長；T為出發(fā)列車j的最晚編組作業(yè)開始時刻，T同理；T表示出發(fā)列車j的出發(fā)時刻，其中T和T為本階段結束時刻，Tcfj'同理；TcJ為出發(fā)列車技術作業(yè)時間；TB為兩編組站的編組作業(yè)時長；gi，j表示到達列車i的解體完畢時刻是否早于出發(fā)列車j的編組開始時刻前，若是，其值為1，否則為0，gi'，j，gi，j'和gi'，j'同理；M是一充分大的正整數(shù)；T為到達列車i的解體作業(yè)開始時刻，T同理；TJ為兩編組站的解體作業(yè)時長；T，T，T，T分別為小運轉列車的編組作業(yè)時長、出發(fā)技術作業(yè)時長、到達技術作業(yè)時長及解體作業(yè)時長；tpq表示列車從P至Q的運行時間，tqp同理。

公式⑸和⑹表示各編組站內(nèi)到達列車的最早解體時刻；公式⑺和⑻表示各編組站內(nèi)出發(fā)列車的最晚編組時刻；公式⑼—⑿表示車流正點接續(xù)約束；公式⒀—⒃表示到達列車與出發(fā)列車之間的接續(xù)時間約束。

（3）不違編約束。

式中：fk，j表示出發(fā)列車j的編組去向是否包括去向k，fk，j'同理，若包括，其值為1，否則為0；hi，k代表到達列車i編組去向是否包括去向k，hi'，k同理，若包括，其值為1，否則為0。

公式⒄—⒇表示出發(fā)列車編組內(nèi)容約束，即各編組站的出發(fā)列車配入的車流，其去向必須在編組計劃的規(guī)定內(nèi)；公式—表示到達列車編組內(nèi)容約束，即只有去向在編組計劃內(nèi)的車流才可編入該出發(fā)列車。

（4）配流代價約束。

式中：wj和wj'為出發(fā)列車排序序號。

（5）出發(fā)列車滿軸要求約束。

式中：Lj和Lj'表示出發(fā)列車滿軸車數(shù)；qj和qj'表示出發(fā)列車的質(zhì)量或長度要求，若必須滿軸則取值為1，否則取值為0。

（6）滿軸判斷約束。

（7）調(diào)機資源約束。

式中：T為出發(fā)列車j的編組作業(yè)開始時刻。

（8）邏輯約束。

3 模型求解

雙編組站靜態(tài)配流協(xié)同優(yōu)化問題需要同時對配流代價和滿軸列車數(shù)進行優(yōu)化，并且變量及約束條件較多，為確保在一定時間內(nèi)求得較優(yōu)方案，提升求解效率，采用理想點法進行求解，首先分別以兩目標函數(shù)構造單目標優(yōu)化模型，求得理想值，然后以兩個優(yōu)化目標與各自理想值的距離和最小為新的目標函數(shù)，將多目標轉化為單目標，具體步驟如下。

步驟1：將目標函數(shù)統(tǒng)一為求最小化，將maxZ2轉化為，其 中Z3表 示 雙編組站總滿軸列車數(shù)。

步驟2：分別以模型中的2 個目標函數(shù)Z1和Z3為目標構造單目標規(guī)劃，分別依次求出Z1min和Z3min，以其求出的最優(yōu)值分別作為該目標的理想值。

步驟3：計算每個目標與理想值的距離，并無量綱化，得到以下評價函數(shù)，其中Z表示無量綱化后的目標函數(shù)值。

步驟4：以minZ作為新的優(yōu)化目標，結合模型約束條件再次求解，所求結果為將2 個優(yōu)化目標綜合考慮求解的最優(yōu)值，故此最優(yōu)解為原多目標規(guī)劃的有效解，即問題的滿意解。

4 算例分析

4.1 算例條件

某樞紐內(nèi)含2 個編組站P 和Q，兩編組站作業(yè)分工既定。編組站P 和Q 均配備解體調(diào)機1 臺和編組調(diào)機1 臺，采用單推單溜駝峰作業(yè)方案。列車編成輛數(shù)取35 輛。到達列車技術作業(yè)時長與出發(fā)列車技術作業(yè)時長均為30 min，解體作業(yè)時長均為15 min，摘掛列車與小運轉列車的編組作業(yè)時長為20 min，直達列車、直通列車、區(qū)段列車的編組作業(yè)時長為15 min。取測試到達階段時段為9：00—13：00，站存車信息表如表1所示。

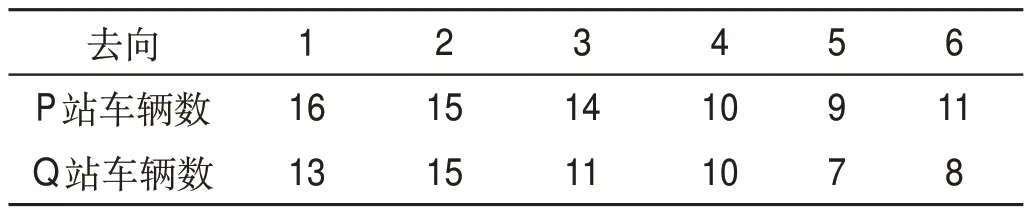
表1 站存車信息表 輛Tab.1 Local wagon data

到達列車車流信息表如表2所示，其中43002，41003，45002，46001為摘掛列車。

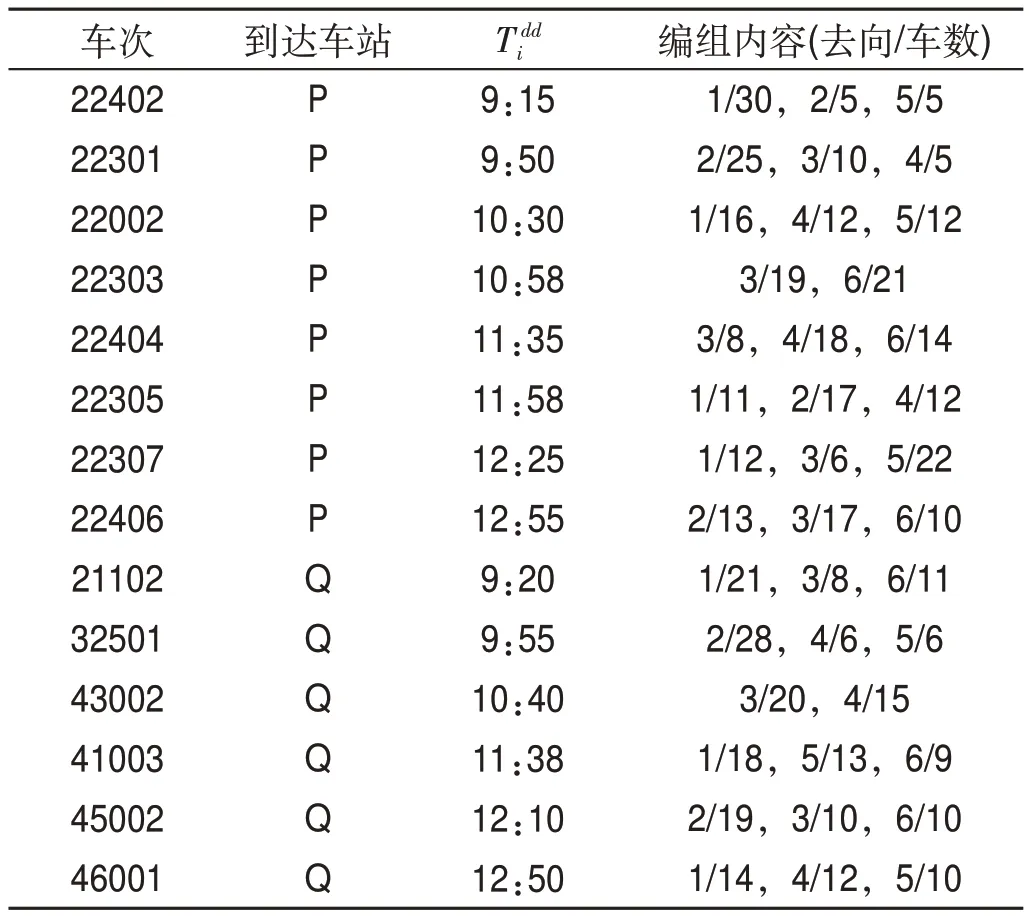
表2 到達列車車流信息表Tab.2 Wagon flow information of arrival trains

取測試出發(fā)階段時段為11：00—15：00，出發(fā)列車車流信息表如表3 所示，其中43101，45202，43001，41004，45001，46002為摘掛列車。

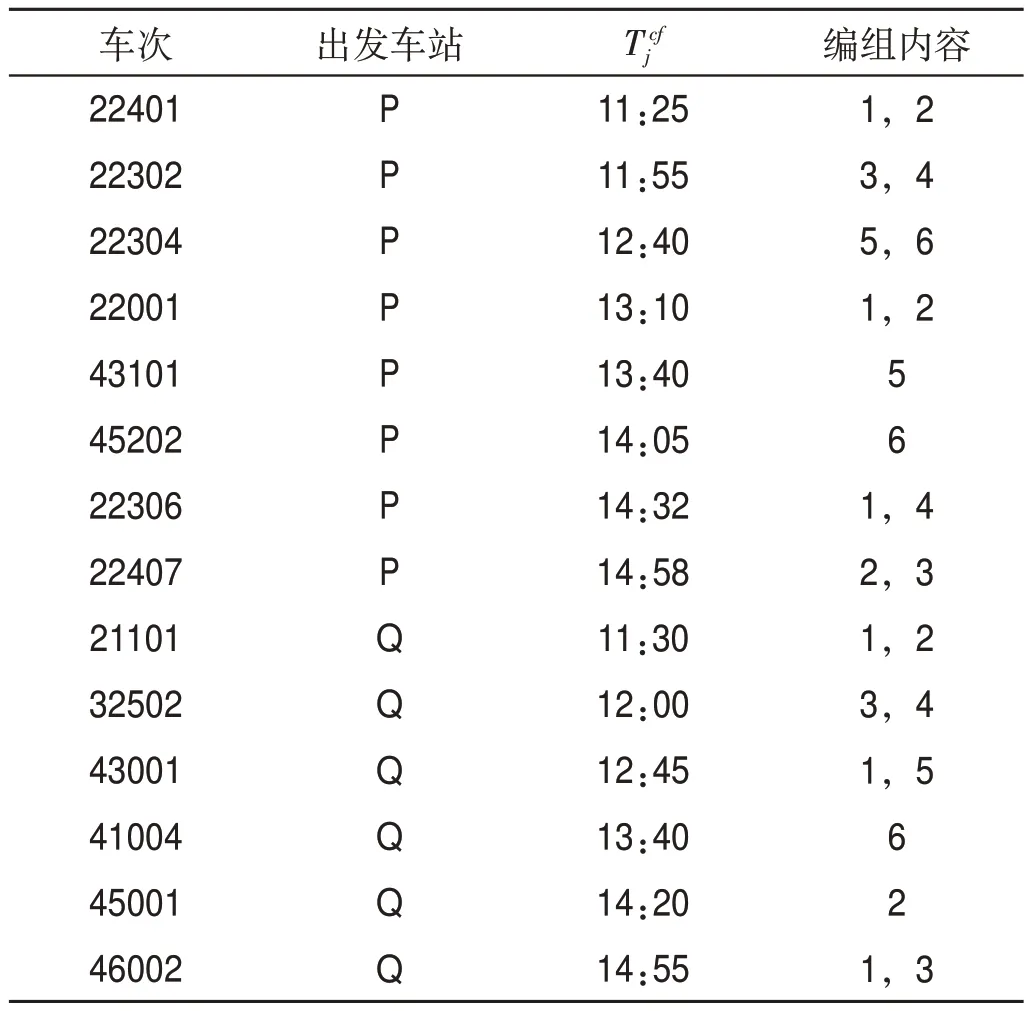
表3 出發(fā)列車車流信息表Tab.3 Wagon flow information of departure trains

4.2 算例求解

按照“先到先解、先發(fā)先編”的順序來確定列車的解編順序，即靜態(tài)配流，由此推算出編組站P到達列車解體作業(yè)信息表如表4 所示，編組站Q 到達列車解體作業(yè)信息表如表5 所示。編組站P 出發(fā)列車編組作業(yè)信息表如表6 所示，編組站Q 出發(fā)列車編組作業(yè)信息表如表7所示。

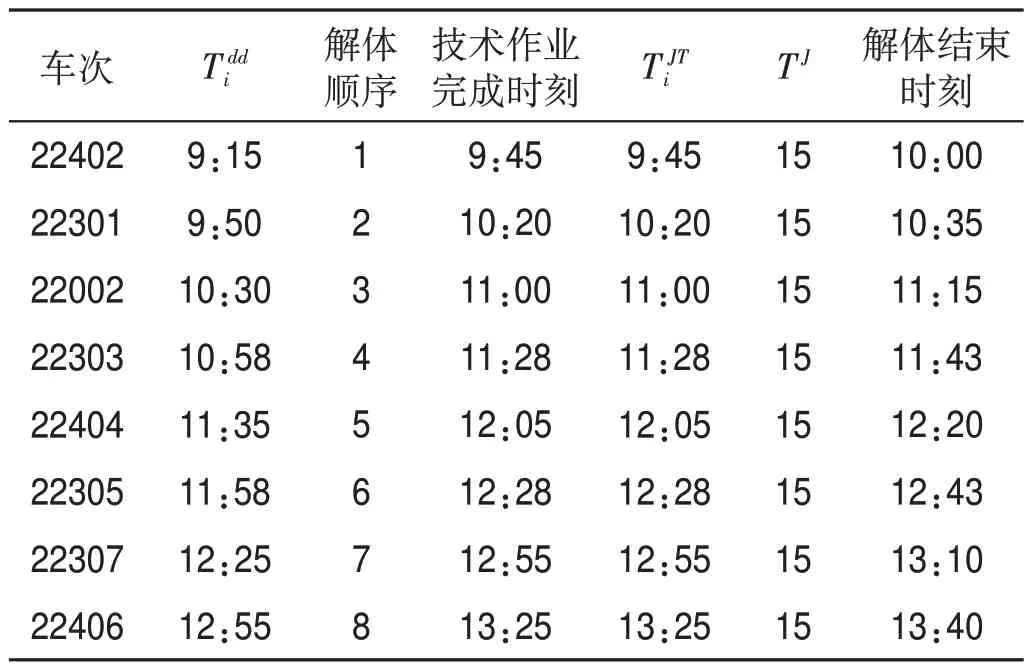
表4 編組站P到達列車解體作業(yè)信息表Tab.4 Break-up information of arrival trains at marshalling station P

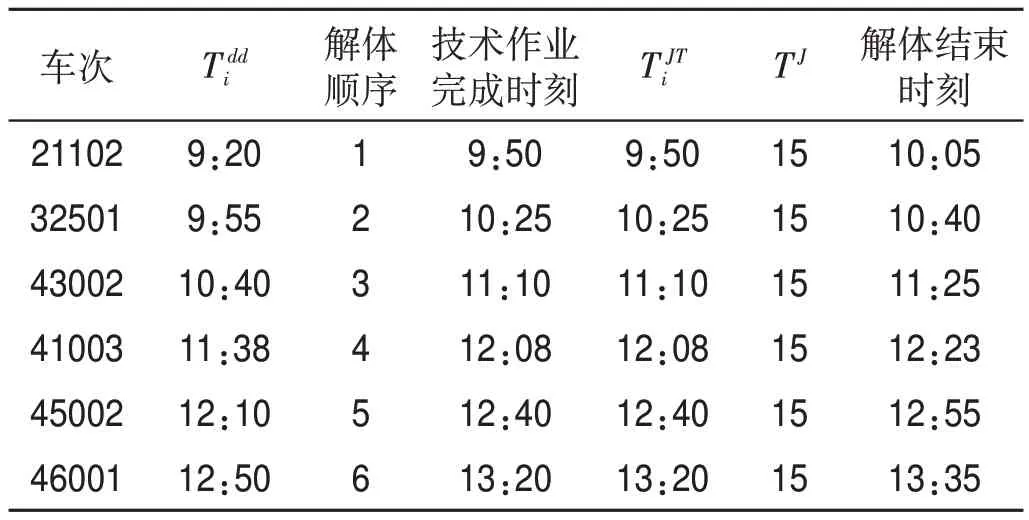
表5 編組站Q到達列車解體作業(yè)信息表Tab.5 Break-up information of arrival trains at marshalling station Q

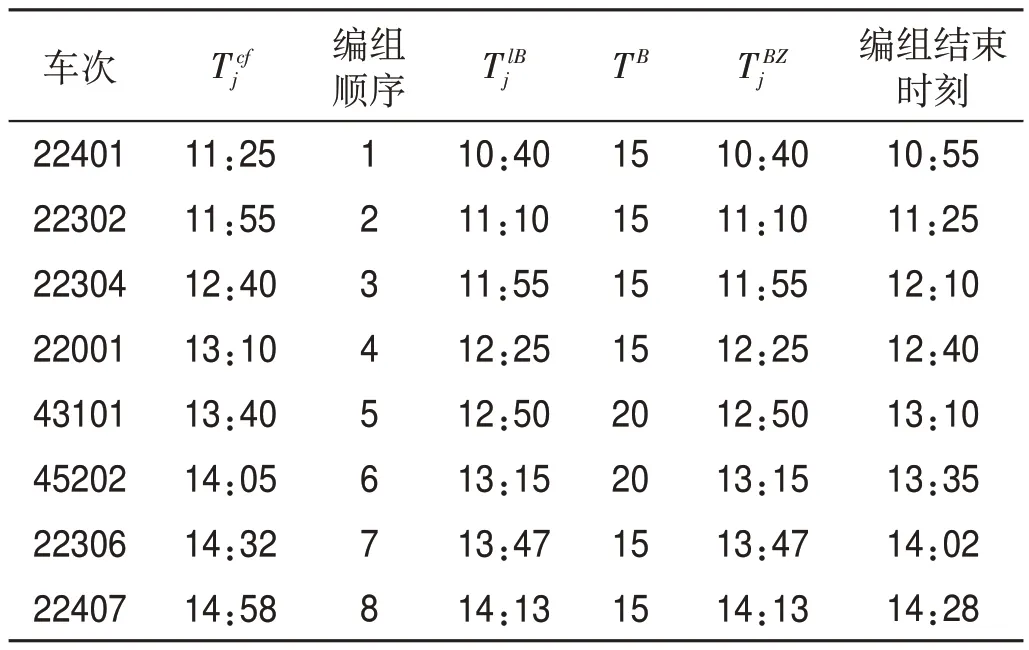
表6 編組站P出發(fā)列車編組作業(yè)信息表Tab.6 Marshalling information of departure trains at marshalling station P

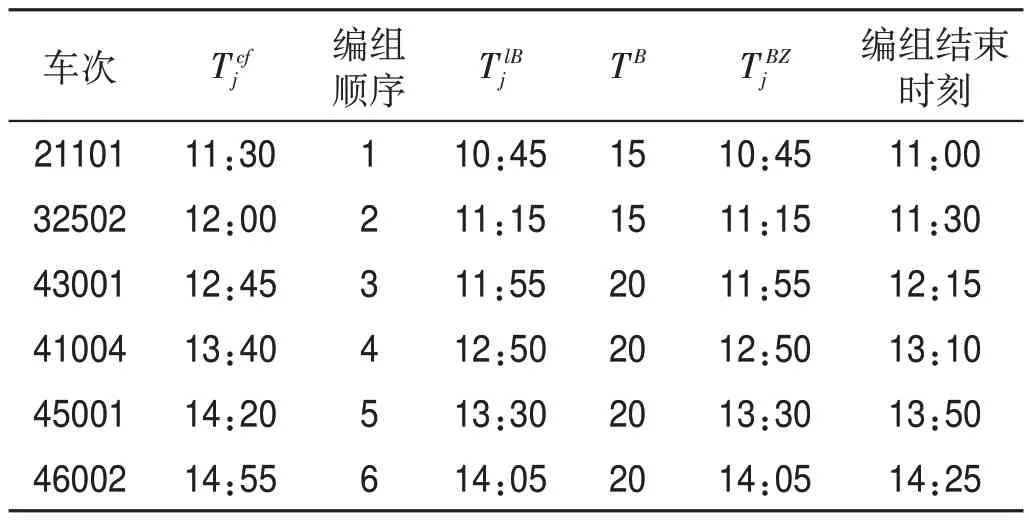
表7 編組站Q出發(fā)列車編組作業(yè)信息表Tab.7 Marshalling information of departure trains at marshalling station Q

依照列車等級、編組內(nèi)容和出發(fā)時刻，編組站P 出發(fā)列車等級排序如表8 所示，編組站Q 出發(fā)列車等級排序如表9所示。

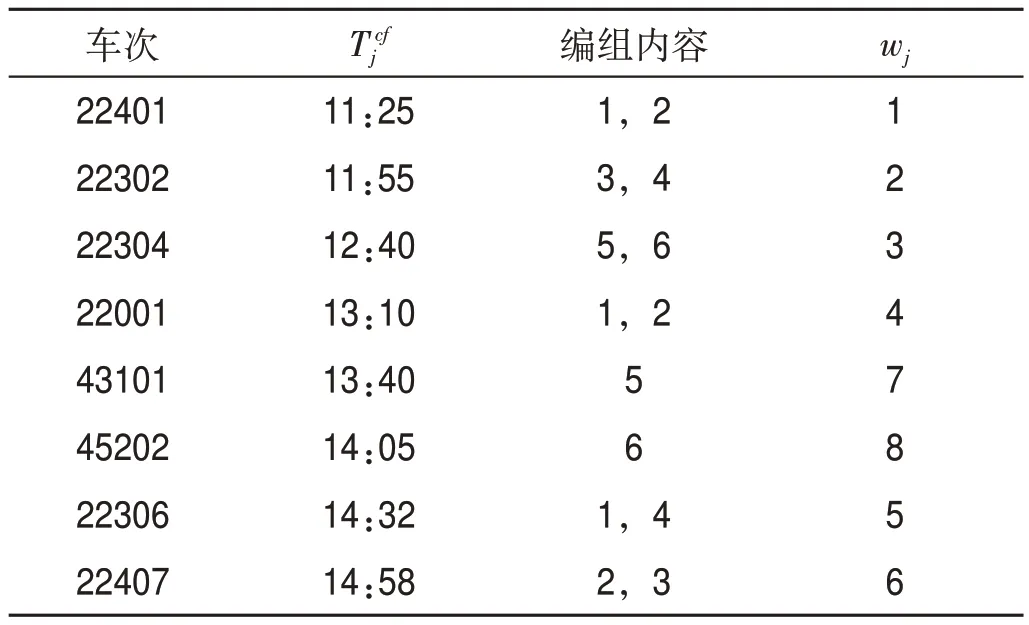
表8 編組站P出發(fā)列車等級排序Tab.8 Class of departure trains at marshalling station P

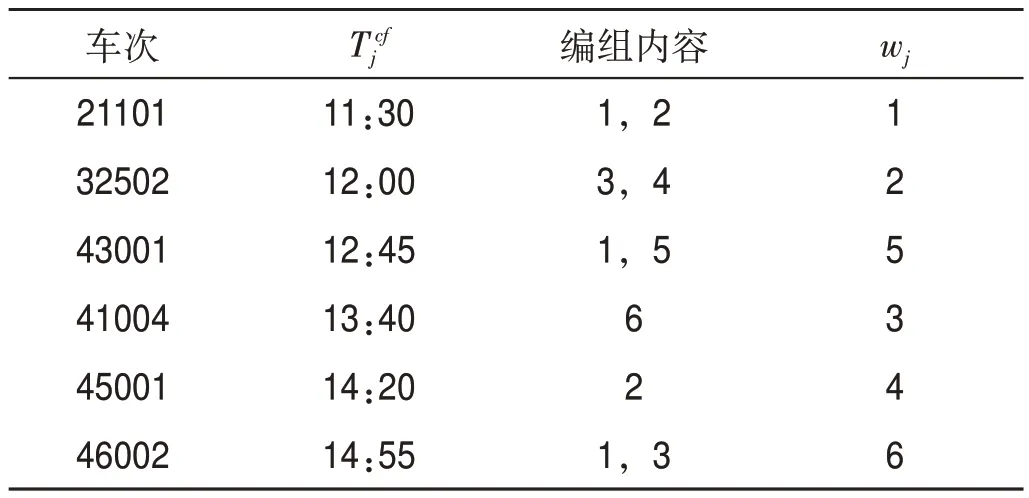
表9 編組站Q出發(fā)列車等級排序Tab.9 Class of departure trains at marshalling station Q

基于算例數(shù)據(jù)以及第3 節(jié)中的模型求解算法，運用數(shù)學軟件對算例進行求解，求得Z1min=2 261 560，Z3min=-12，通過理想點算法求得編組站P配流方案如表10所示，編組站Q配流方案如表11所示，編組站P 階段結束時站存車情況如表12 所示，編組站Q 階段結束時站存車情況如表13所示。

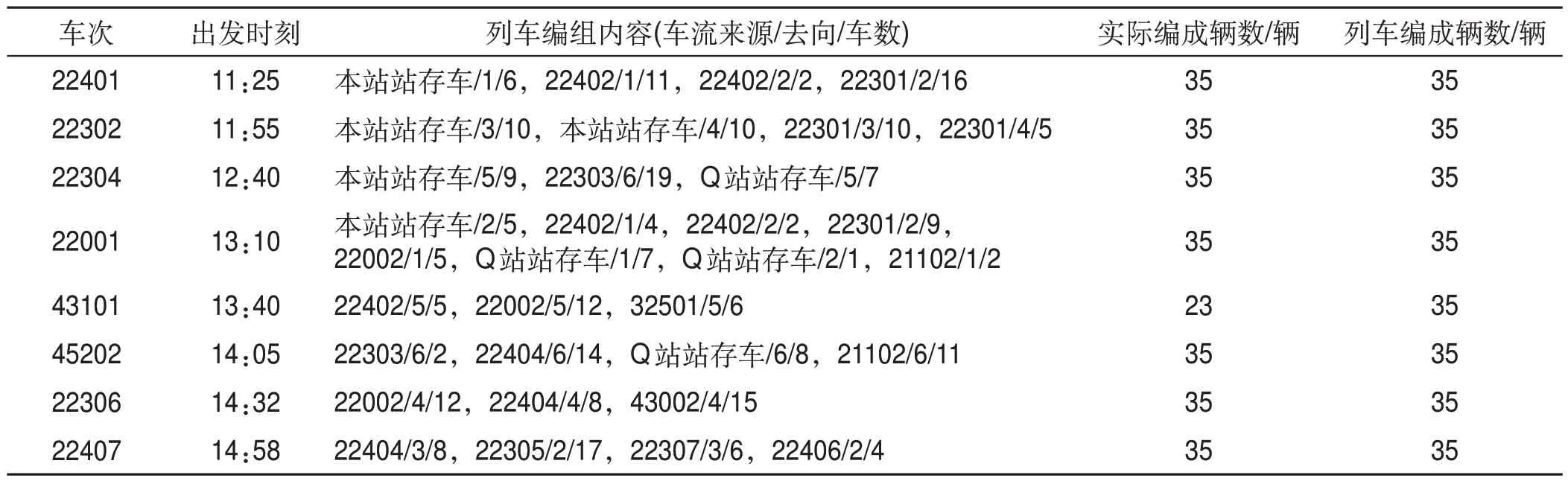
表10 編組站P配流方案Tab.10 Wagon-flow allocation scheme of marshalling station P

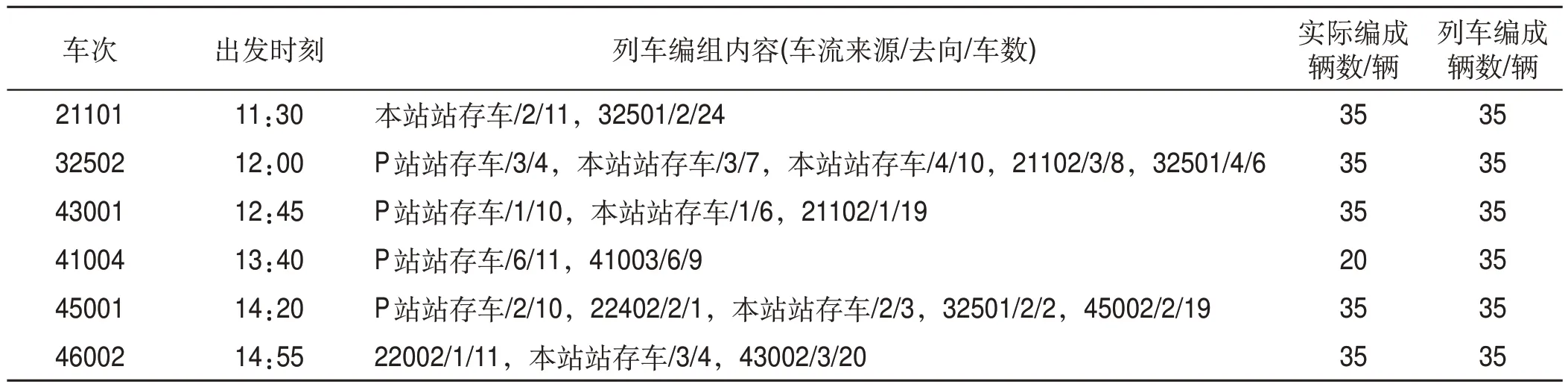
表11 編組站Q配流方案Tab.11 Wagon-flow allocation scheme of marshalling station Q

表12 編組站P階段結束時站存車情況Tab.12 Remained local cars at marshalling station P

表13 編組站Q階段結束時站存車情況Tab.13 Remained local cars at marshalling station Q

為檢驗該模型的優(yōu)化效果，求出各編組站分別配流的結果，對比雙編組站聯(lián)合配流及各編組站分別配流，配流效果對比如表14所示。

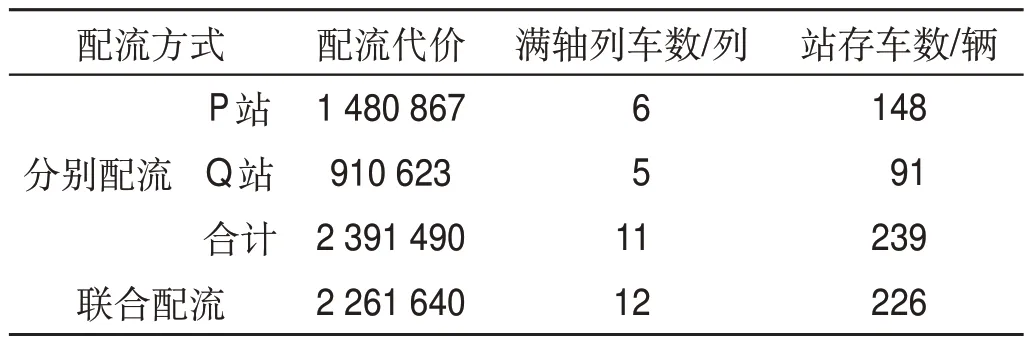
表14 配流效果對比Tab.14 Contrast of wagon-flow allocation effect

將對比結果進一步整理分析，出發(fā)列車滿軸率對比圖如圖2所示。

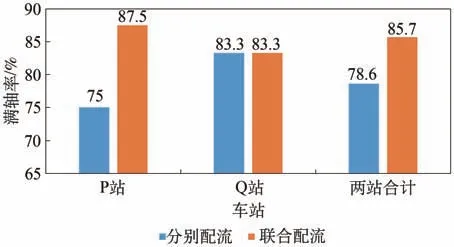
圖2 出發(fā)列車滿軸率對比圖Fig.2 Contrast of full-axle rate for departure trains

模型與求解方法可快速求得雙編組站協(xié)同配流方案，與人工編制計劃相比，可大幅節(jié)約時間、減少勞動強度。由表10—表13 可得，出發(fā)列車中除摘掛列車43101，41004 外，均滿軸出發(fā)。由表14可知，聯(lián)合配流的配流代價為2 261 640，分別配流的配流代價總和為2 391 490，降低5.4%；聯(lián)合配流滿軸列車數(shù)為12列，分別配流的滿軸列車數(shù)總和為11列，提升9.1%；聯(lián)合配流站存車數(shù)為226輛，分別配流的站存車數(shù)總和為239輛，降低5.4%，具有較好的優(yōu)化效果。根據(jù)圖2，聯(lián)合配流時，編組站P 與編組站Q 的出發(fā)列車滿軸率分別為87.5%和83.3%，兩站平均出發(fā)列車滿軸率為85.7%大于兩編組站分別獨立配流的總滿軸率78.6%。

研究結果表明，針對擁有多編組站的鐵路樞紐，聯(lián)合配流可提升滿軸率，保證更多的列車正點滿軸。提出的模型及算法能在鐵路樞紐全局角度，進行跨編組站協(xié)同靜態(tài)配流，可為鐵路樞紐整體運輸組織水平的提升提供一定的參考價值。

5 結束語

從樞紐內(nèi)雙編組站配流協(xié)同優(yōu)化的角度出發(fā)，考慮不違編約束、配流代價約束、車流接續(xù)約束等約束條件，建立鐵路樞紐雙編組站靜態(tài)配流協(xié)同優(yōu)化模型，并根據(jù)模型特點設計理想點算法求解，以此減少樞紐內(nèi)兩編組站的配流總代價及站存車總數(shù)，增加兩編組站的總滿軸列車數(shù)。最后通過算例及對比結果分析驗證模型及算法的有效性，相比兩編組站單獨配流，兩編組站聯(lián)合配流的配流代價降低5.4%，站存車數(shù)減少13輛，滿軸列車數(shù)增加1列，可有效提升樞紐內(nèi)車輛周轉率。當列車密集到發(fā)時，動態(tài)配流的引入，合理調(diào)整列車解編順序有待進一步研究。